Распределение ферми дирака кратко

Обновлено: 04.07.2024

Если все однородные частицы в квантовой физике абсолютно тождественны, то есть неотличимы друг от друга, то как же описать их состояние? Вот тут на первый план и выходит квантовая статистика. А поскольку фермионы и бозоны ведут себя отлично друг от друга, начнем рассказ с фермионов.

В классической физике все микрочастицы в принципе различимы, в квантовой же физике различия между одинаковыми частицами нет! Поэтому все описание сводится к статистическому анализу вероятности событий.

Выше мы описали понятие спина и указали, что частицы, имеющие спин, равный %, называются фермионами. К фермионам относится, например, электрон. В отличие от бозонов, имеющих спин, равный 1, фермионы подчиняются принципу Паули, чего нельзя сказать о бозонах.

Неразличимые близнецы, или одно и то же

Описанием поведения частиц занимается квантовая статистика — раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

Статистика Ферми — Дирака была предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил ее квантово-механический смысл.

Он нас посчитал!

Природа же квантовых частиц не позволяет отличить их друг от друга. Если две тождественные частицы, то есть частицы с одинаковыми массами, зарядом, спином и так далее, взаимодействуют, то мы не можем выяснить, какая из двух частиц была первая, а какая вторая. В квантовой физике действует принцип неразличимости тождественных частиц: тождественных частицы экспериментально различить принципиально невозможно.

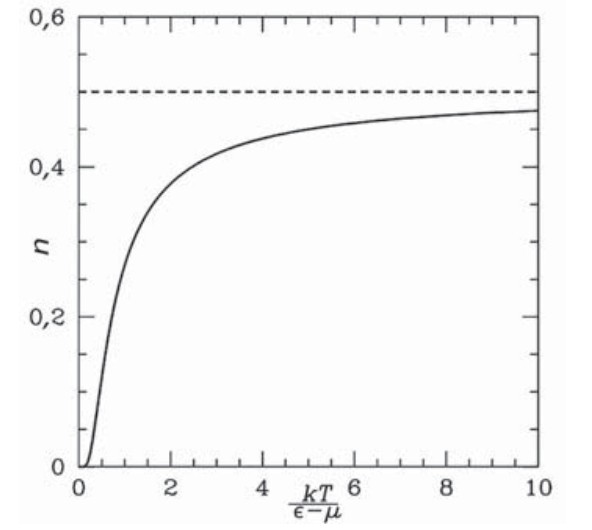
Распределение Ферми — Дирака: высокоэнергетические состояния имеют меньшую вероятность, а низкоэнергетические более вероятны

Для описания поведения систем фермионов и их вероятного распределения по энергетическим уровням применяется статистическое распределение Ферми — Дирака. Еще раз напомним, что фермионы (электроны, протоны, нейтроны и др.) подчиняются принципу запрета Паули. В таких системах в одном квантовом состоянии может находиться не более одной частицы. Согласно этой статистике и описывается вероятность того, что состояние с некоторой энергией E при температуре Т будет занято электроном.

Итак, распределение Ферми — Дирака математически отражает суть поведения частиц с полуцелым спином: присутствие фермиона в конкретном квантовом состоянии запрещает другим фермионам находиться в том же состоянии.

Статистика Ферми — Дирака в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние может занимать не более одной частицы); определяет статистическое распределение фермионов по энергетическим уровням системы, находящейся в термодинамическом равновесии; предложена в 1926 г. итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам в металле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией ε_i есть

$n_i = \frac<g_i> <e^<(\epsilon_i-\mu) / k T>+ 1>$

— среднее число частиц в состоянии i, — энергия состояния i, — кратность вырождения состояния i (число состояний с энергией ), μ — химический потенциал (который равен энергии Ферми при абсолютном нуле температуры), k — постоянная Больцмана, T — абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур . В этом случае (полагая уровни энергии невырожденными ), функция распределения частиц называется функцией Ферми:

$F(E) = \frac<1> + 1>$

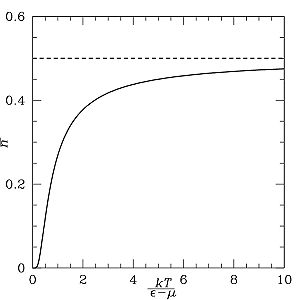
Распределение Ферми — Дирака как функция температуры. Заполнение уровней с энергиями ε > μ растёт с увеличением температуры

Содержание

Применение

Вывод распределения

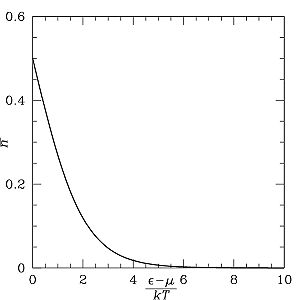
Распределение Ферми — Дирака как функция от ε. Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергитические состояния более вероятны

$Z \;= \sum_s e^< -( E(s) - \mu N(s) ) / kT> $

— энергия состояния s, — число частиц, находящихся в состоянии s, μ — химический потенциал, s — это индекс, пробегающий все возмножные микросостояния системы.

$n \cdot \epsilon$

В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято n частицами, то энергия системы — . Если состояние свободно, то энергия имеет значение 0. Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и тоже физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся s₁ and s₂ соответственно. Видно, что , , и , . Поэтому функция распределения принимает вид:

$Z = \sum_ ^2 e^ < -( E(s_i) - \mu N(s_i) ) / kT>= e^ < -( \epsilon - \mu ) / kT>+ 1$
.

Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии s_α вычисляется по формуле

$P( s_ ) = \frac) - \mu N(s_)> >$
.

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии s₁ , вероятность которого

$\bar<n> = P( s_1 ) = \frac < e^< -( E(s_1) - \mu N(s_1) ) / kT>> = \frac> + 1> = \frac + 1>$
.

" width="" height="" />
называется распределением Ферми — Дирака. Для фиксированной температуры T, (\epsilon)" width="" height="" />
есть вероятность того, что состояние с энергией ε будет занято фермионом. Обратите внимание, что " width="" height="" />
является убывающей функцией от ε. Это соответствует нашим ожиданиям: высокоэнергетические состояния занимаются с меньшей вероятностью.

$\; g_<\epsilon> Обратите внимание, что энергетический уровень ε имеет вырождение$
. Теперь можно произвести простую модификацию:

$\bar<n> = g_ \cdot \frac + 1>$
.

Это число — ожидаемое число частиц, в суммарном состоянии с энергией ε.

$\bar<n> Для всех температур T, (\mu) = \frac$
. Это означает, что состояния с энергией μ всегда будут иметь одинаковую вероятность быть заполнеными или свободными.

В пределе , " width="" height="" />
становится ступенчатой функцией (см. первый график). Все состояния с энергией меньше химического потенциала μ будут заняты с вероятностью 1. Состояния с энергией выше химического потенциала μ будут свободны. Химический потенциал при нулевой температуре — энергия Ферми, обозначается E_F , то есть

$E _F = \; \mu(T = 0)$

Влияние температуры

Необходимо заметить, что химический потенциал зависит от температуры. Однако для систем, имеющих температуру ниже температуры Ферми " width="" height="" />
, что часто используется, как аппроксимация " width="" height="" />
≈ . В реальности же:

$\mu = E _F \left[ 1- \frac<\pi ^2> \left(\frac\right) ^2 + \frac<\pi^4> \left(\frac\right)^4 + \cdots \right]$

В полупроводниках различают три энергетических зоны: валентную зону, запрещённую зону и зону проводимости.

Валентная зона - энергетическая область разрешённых электронных состояний в полупроводнике, заполненная валентными электронами.

Зона проводимости - диапазон энергии, где могут находиться свободные электроны из валентной зоны, преодолевшие запрещённую зону.

Распределение электронов и дырок по энергиям подчиняется статистическим законам Ферми-Дирака и Максвелла-Больцмана.

Распределение Ферми-Дирака определяет статистическое распределение заряженных частиц по энергетическим уровням системы, находящейся в термодинамическом равновесии. В статистике Ферми-Дирака среднее число частиц в состоянии с энергией ε есть

Функция распределения для вырожденного коллектива фермионов впервые была получена итальянским физиком Энрико Ферми и английским физиком Полем Дираком:

Химический потенциал μ для фермионов обычно называют энергией, или уровнем Ферми – Е_Ф.

Анализ выражения показывает, что при Е=Е_Ф и температуре Т>0, f_Ф(Е)=½, т.е. вероятность заселения уровня Ферми при Т>0 равна ½.

Для того чтобы понять свойства функции Ферми-Дирака, полезно рассмотреть ее поведение при Т=0. Проводник можно представить в виде потенциальной ямы для электронов, выход из которой требует совершения работы по преодолению сил связи, удерживающих электроны – работы выхода (рис. 3.3, а). На рисунке показаны энергетические уровни, которые могут занимать электроны. Согласно постулату Паули, на каждом уровне может располагаться не более двух электронов (с противоположными спинами).

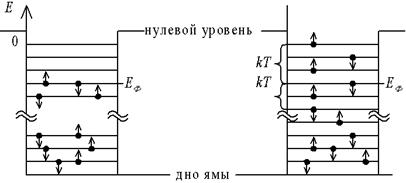
Как видно на рисунке, при Т=0 все уровни ниже уровня Ферми заняты, а все уровни выше этого уровня пусты, т.е. функция f_Ф(Е) при Т=0 имеет форму ступеньки (рис. 3.4, а).

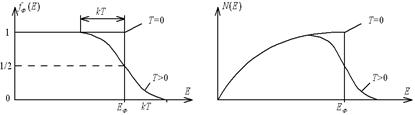
Рис. 3.4. Распределение Ферми-Дирака: а – функция распределения Ф-Д;
б – полная функция распределения

Таким образом можно определить физический смысл уровня Ферми, но только для проводников. В случае полупроводников или изоляторов это определение неприемлемо, поскольку в этих материалах недостаточно свободных электронов и уровень Ферми находится в запрещенной зоне (п. 4.5).

Умножив функцию распределения (3.20) на число состояний (3.13), получим выражение для полной функции распределения при Т=0 (рис. 3.4, б)

Проинтегрировав (3.21) в указанном интервале энергий, будем иметь выражение для энергии Ферми:

где n – концентрация электронного газа в проводнике.

Используя выражение (3.21), можно получить формулы для вычисления средней энергии – и максимальной скорости электронов при абсолютном нуле

Необходимо отметить, что кинетическая энергия электронов Е_Ф не является тепловой энергией, а имеет чисто квантовую природу и определяется свойствами электронов как Ферми-частиц.

С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни (см. рис. 3.3, б). Происходит “размывание” функций распределения (см. рис. 3.4), и ступенька Е=Е_Ф преобразуется в интервал, ширина которого равна 2kT. Однако более глубокие состояния электронов остаются неизменными.

Проведенные расчеты показывают, что число термически возбужденных частиц составляет для комнатной температуры всего 1-2% от общего числа. Если проинтегрировать полную функцию распределения во всем энергетическом диапазоне, то можно получить выражение для температурной зависимости энергии Ферми

Напомним, что тепловое возбуждение так незначительно влияет на характеристики вырожденного Ферми-газа, что во многих случаях этим влиянием можно пренебречь и считать Е_Ф = Е_Ф_о во всем температурном диапазоне.

Можно также вычислить среднюю энергию электронов при ненулевой температуре Т>0

где Е_п – полная энергия электронного газа.

Ранее мы говорили о Ферми-газе, считая его вырожденным коллективом. Однако, в случае выполнения критерия (3.11) G>>N, можно говорить о снятии вырождения. Тогда критерий невырожденности (3.11) примет вид

или в случае Е=0

Из последнего соотношения следует, что для невырожденного Ферми-газа должно выполняться условие

При выполнении условия (3.27) единицей в знаменателе выражения (3.20) можно пренебречь, и выражение (3.20) совпадает с формулой для функции Максвелла-Больцмана.

В проводниках, где концентрация электронов высока, электронный газ всегда находится в вырожденном состоянии. С невырожденным электронным газом приходится сталкиваться в собственных (беспримесных) и слаболегированных (10 16 . 10 24 м -3 ) полупроводниках. При таких условиях выполняется критерий (3.11) и электронный газ млжно считать невырожденным. Поэтому уместно, на наш взгляд, привести таблицу, где содержатся основные характеристики электронного газа: его средняя энергия, квадратичная скорость υ_кв, импульс P (табл. 3.2).

Параметры электронного газа [15]

Параметры газа	Газ
невырожденный	вырожденный
, Т=0 Т>0
J_кв, Т=0 Т>0	м/с
Р, Т=0 Т>0	≈10 10 Па Р ≈ Р₀

Из данных таблицы видно, что параметры вырожденного газа в отличие от газа невырожденного при нулевой температуре не равны нулю и практически не зависят от температуры. Это, в свою очередь, говорит о нетепловом квантовомеханическом характере данных процессов.

Химический потенциал μ для фермионов обычно называют энергией, или уровнем Ферми – Е_Ф.

Рис. 3.4. Распределение Ферми-Дирака: а – функция распределения Ф-Д;
б – полная функция распределения

Проинтегрировав (3.21) в указанном интервале энергий, будем иметь выражение для энергии Ферми:

где n – концентрация электронного газа в проводнике.

Можно также вычислить среднюю энергию электронов при ненулевой температуре Т>0

где Е_п – полная энергия электронного газа.

или в случае Е=0

Из последнего соотношения следует, что для невырожденного Ферми-газа должно выполняться условие

Параметры электронного газа [15]

Параметры газа	Газ
невырожденный	вырожденный
, Т=0 Т>0
J_кв, Т=0 Т>0	м/с
Р, Т=0 Т>0	≈10 10 Па Р ≈ Р₀

При абсолютном нуле в каждом из состояний, энергия которых не превышает находится один электрон; в состояниях с электроны отсутствуют. Следовательно, функция распределения электронов по состояниям с различной энергией имеет при абсолютном нуле вид, показанный на рис. 52.1.

Найдем функцию распределения при температуре, отличной от абсолютного нуля.

Следуя Киттелю, рассмотрим неупругие столкновения равновесного электронного газа с атомом примеси, внедренным в кристаллическую решетку металла. Допустим, что атом примеси может находиться лишь в двух состояниях, энергию которых мы положим равной 0 и .

Из множества процессов столкновений рассмотрим тот, в результате которого электрон переходит из состояния к с энергией Е в состояние к с энергией . Атом примеси переходит при этом с уровня с энергией на уровень с энергией, равной нулю. Вероятность перехода к пропорциональна: 1) вероятности того, что состояние занято электроном, 2) вероятности того, что состояние свободно, 3) вероятности того, что атом примеси находится в состоянии с энергией е. Таким образом,

Вероятность обратного процесса пропорциональна выражению

где - вероятность того, что атом примеси находится в состоянии с энергией, равной нулю.

В силу принципа детального равновесия коэффициент пропорциональности в выражениях (52.1) и (52.2) одинаков.

В равновесном состоянии вероятности переходов должны быть одинаковыми. Следовательно,

(мы учли, что вероятности нахождения атома примеси на уровнях подчиняются закону распределения Больцмана).

Функциональное уравнение (52.3) должно выполняться при любой температуре Т. Это произойдет, если положить

где — величина, не зависящая от Е. Соответственно

Произведение этих двух выражений при любой температуре равно

Решив уравнение (52.4) относительно получим для функции распределения электронов по состояниям с различной энергией выражение

Это выражение называется функцией распределения Ферми — Дирака. Параметр носит название химического потенциала.

В соответствии со смыслом функции (52.5) величина представляет собой среднее число электронов, находящихся в состоянии с энергией Е. Поэтому формуле (52.5) можно придать вид

(ср. с (49.4)). В отличие от (49.4), параметр в распределении (52.6) имеет положительные значения (в данном случае это не приводит к отрицательным значениям чисел ). Распределение (52.6) лежит в основе статистики Ферми—Дирака.

Частицы, подчиняющиеся этой статистике, называются фермионами. К их числу относятся все частицы с полуцелым спином.

Имеющий размерность энергии параметр часто обозначается через и называется уровнем Ферми или энергией Ферми. В этих обозначениях функция (52.5) имеет вид

Исследуем свойства функции (52.7). При абсолютном нуле

Таким образом, при 0 К уровень Ферми ЕР совпадает с верхним заполненным электронами уровнем (см. предыдущий параграф).

Независимо от значения температуры, при функция равна Следовательно, уровень Ферми совпадает с тем энергетическим уровнем, вероятность заполнения которого равна половине.

Значение ЕР можно найти из условия, что полное число электронов, заполняющих уровни, должно равняться числу свободных электронов в кристалле ( — плотность электронов, V — объем кристалла). Количество состояний, приходящееся на интервал энергий , равно где — плотность состояний. Среднее число электронов, находящихся в случае теплового равновесия в этих состояниях, определяется выражением Интеграл от этого выражения даст полное число свободных электронов в кристалле:

Это соотношение представляет собой по существу условие нормировки функции

Подстановка в (52.8) выражений (51.9) и (52.7) дает

Это соотношение позволяет в принципе найти как функцию . Интеграл в выражении (52.9) не берется. При условии, что удается найти приближенное значение интеграла. В результате для уровня Ферми получается выражение

(напомним, что ) зависит от ; см. (51.10)).

Из (52.10) следует, что при низких температурах (для которых только и справедливо это выражение) уровень Ферми хотя и зависит от температуры, но очень слабо. Поэтому во многих случаях можно полагать Однако для понимания, например, термоэлектрических явлений (см. § 63) зависимость от Т имеет принципиальное значение.

т. е. переходит в функцию распределения Больцмана.

Отметим, что заметное отличие кривой на рис. 52.2 от графика, изображенного на рис. 52.1, наблюдается лишь в области порядка Чем выше температура, тем более полого идет ниспадающий участок кривой.

Поведение электронного газа в сильной степени зависит от соотношения между температурой кристалла и температурой Ферми, равной Различают два предельных случая.

1. . В этом случае электронный газ называется вырожденным.

2. . В этом случае электронный газ называется невырожденным.

В предыдущем параграфе мы установили, что температура Ферми для металлов составляет несколько десятков тысяч кельвин. Поэтому даже при температуре, близкой к температуре плавления металла электронный газ в металле является вырожденным. В полупроводниках плотность свободных электронов оказывается много меньшей, чем в металлах. Соответственно мало ( приближенно пропорционально ; см. (52.10) и (51.10)).

Поэтому уже при комнатной температуре электронный газ во многих полупроводниках является невырожденным и подчиняется классической статистике.

Читайте также: