Рациональное выражение это кратко

Обновлено: 07.07.2024

Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.

Определение и примеры рациональных выражений

Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.

Для примера имеем, что 5 , 2 3 · x - 5 , - 3 · a · b 3 - 1 c 2 + 4 a 2 + b 2 1 + a : ( 1 - b ) , ( x + 1 ) · ( y - 2 ) x 5 - 5 · x · y · 2 - 1 11 · x 3 .

То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.

Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.

Основные виды преобразований рациональных выражений

Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.

Преобразовать рациональное выражение 3 · x x · y - 1 - 2 · x x · y - 1 .

Видно, что такое рациональное выражение – это разность 3 · x x · y - 1 и 2 · x x · y - 1 . Замечаем, что знаменатель у них идентичный. Это значит, что приведение подобных слагаемых примет вид

3 · x x · y - 1 - 2 · x x · y - 1 = x x · y - 1 · 3 - 2 = x x · y - 1

Ответ: 3 · x x · y - 1 - 2 · x x · y - 1 = x x · y - 1 .

Выполнить преобразование 2 · x · y 4 · ( - 4 ) · x 2 : ( 3 · x - x ) .

Первоначально выполняем действия в скобках 3 · x − x = 2 · x . Данное выражение представляем в виде 2 · x · y 4 · ( - 4 ) · x 2 : ( 3 · x - x ) = 2 · x · y 4 · ( - 4 ) · x 2 : 2 · x . Мы приходим к выражению, которое содержит действия с одной ступенью, то есть имеет сложение и вычитание.

Избавляемя от скобок при помощи применения свойства деления. Тогда получаем, что 2 · x · y 4 · ( - 4 ) · x 2 : 2 · x = 2 · x · y 4 · ( - 4 ) · x 2 : 2 : x .

Группируем числовые множители с переменной x , после этого можно выполнять действия со степенями. Получаем, что

2 · x · y 4 · ( - 4 ) · x 2 : 2 : x = ( 2 · ( - 4 ) : 2 ) · ( x · x 2 : x ) · y 4 = - 4 · x 2 · y 4

Ответ: 2 · x · y 4 · ( - 4 ) · x 2 : ( 3 · x - x ) = - 4 · x 2 · y 4 .

Преобразовать выражение вида x · ( x + 3 ) - ( 3 · x + 1 ) 1 2 · x · 4 + 2 .

Для начала преобразовываем числитель и знаменатель. Тогда получаем выражение вида ( x · ( x + 3 ) - ( 3 · x + 1 ) ) : 1 2 · x · 4 + 2 , причем действия в скобках делают в первую очередь. В числителе выполняются действия и группируются множители. После чего получаем выражение вида x · ( x + 3 ) - ( 3 · x + 1 ) 1 2 · x · 4 + 2 = x 2 + 3 · x - 3 · x - 1 1 2 · 4 · x + 2 = x 2 - 1 2 · x + 2 .

Преобразуем в числителе формулу разности квадратов, тогда получаем, что

x 2 - 1 2 · x + 2 = ( x - 1 ) · ( x + 1 ) 2 · ( x + 1 ) = x - 1 2

Ответ: x · ( x + 3 ) - ( 3 · x + 1 ) 1 2 · x · 4 + 2 = x - 1 2 .

Представление в виде рациональной дроби

Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.

Представить в виде рациональной дроби a + 5 a · ( a - 3 ) - a 2 - 25 a + 3 · 1 a 2 + 5 · a .

Данное выражение можно представить в виде a 2 - 25 a + 3 · 1 a 2 + 5 · a . Умножение выполняется в первую очередь по правилам.

Следует начать с умножения, тогда получим, что

a 2 - 25 a + 3 · 1 a 2 + 5 · a = a - 5 · ( a + 5 ) a + 3 · 1 a · ( a + 5 ) = a - 5 · ( a + 5 ) · 1 ( a + 3 ) · a · ( a + 5 ) = a - 5 ( a + 3 ) · a

Производим представление полученного результата с исходное. Получим, что

a + 5 a · ( a - 3 ) - a 2 - 25 a + 3 · 1 a 2 + 5 · a = a + 5 a · a - 3 - a - 5 a + 3 · a

Теперь выполняем вычитание:

a + 5 a · a - 3 - a - 5 a + 3 · a = a + 5 · a + 3 a · ( a - 3 ) · ( a + 3 ) - ( a - 5 ) · ( a - 3 ) ( a + 3 ) · a · ( a - 3 ) = = a + 5 · a + 3 - ( a - 5 ) · ( a - 3 ) a · ( a - 3 ) · ( a + 3 ) = a 2 + 3 · a + 5 · a + 15 - ( a 2 - 3 · a - 5 · a + 15 ) a · ( a - 3 ) · ( a + 3 ) = = 16 · a a · ( a - 3 ) · ( a + 3 ) = 16 a - 3 · ( a + 3 ) = 16 a 2 - 9

После чего очевидно, что исходное выражение примет вид 16 a 2 - 9 .

Ответ: a + 5 a · ( a - 3 ) - a 2 - 25 a + 3 · 1 a 2 + 5 · a = 16 a 2 - 9 .

Представить x x + 1 + 1 2 · x - 1 1 + x в виде рациональной дроби.

Заданное выражение записывается как дробь, в числителе которой имеется x x + 1 + 1 , а в знаменателе 2 · x - 1 1 + x . Необходимо произвести преобразования x x + 1 + 1 . Для этого нужно выполнить сложение дроби и числа. Получаем, что x x + 1 + 1 = x x + 1 + 1 1 = x x + 1 + 1 · ( x + 1 ) 1 · ( x + 1 ) = x x + 1 + x + 1 x + 1 = x + x + 1 x + 1 = 2 · x + 1 x + 1

Следует, что x x + 1 + 1 2 · x - 1 1 + x = 2 · x + 1 x + 1 2 · x - 1 1 + x

Получившаяся дробь может быть записана как 2 · x + 1 x + 1 : 2 · x - 1 1 + x .

После деления придем к рациональной дроби вида

2 · x + 1 x + 1 : 2 · x - 1 1 + x = 2 · x + 1 x + 1 · 1 + x 2 · x - 1 = 2 · x + 1 · ( 1 + x ) ( x + 1 ) · ( 2 · x - 1 ) = 2 · x + 1 2 · x - 1

Можно решить это иначе.

Вместо деления на 2 · x - 1 1 + x производим умножение на обратную ей 1 + x 2 · x - 1 . Применим распределительное свойство и получаем, что

x x + 1 + 1 2 · x - 1 1 + x = x x + 1 + 1 : 2 · x - 1 1 + x = x x + 1 + 1 · 1 + x 2 · x - 1 = = x x + 1 · 1 + x 2 · x - 1 + 1 · 1 + x 2 · x - 1 = x · 1 + x ( x + 1 ) · 2 · x - 1 + 1 + x 2 · x - 1 = = x 2 · x - 1 + 1 + x 2 · x - 1 = x + 1 + x 2 · x - 1 = 2 · x + 1 2 · x - 1

Поурочное планирование по алгебре для 8 класса. Ориентировано на работу с УМК Макарычев. Алгебра 8 класс. Просвещение. Глава 1. Рациональные дроби. § 1. Рациональные дроби и их свойства (5 ч). Уроки 1-2. Рациональные выражения. Вернуться к Списку уроков Тематического планирования.

Уроки 1-2. Рациональные выражения

Цель: рассмотреть рациональные выражения и допустимые значения переменных в них.
Планируемые результаты: освоить виды алгебраических выражений, понятие допустимых значений переменных.
Тип уроков: уроки общеметодологической направленности.

ХОД УРОКОВ

II. Работа по теме уроков

План уроков

Виды алгебраических выражений.
Допустимые значения переменных в выражении.

1. Виды алгебраических выражений

Напомним основные понятия, введенные в 7 классе. Алгебраическим выражением называется выражение, составленное из чисел и переменных с помощью действий сложения, вычитания, умножения, деления, возведения в степень и с помощью скобок.

Пример 1

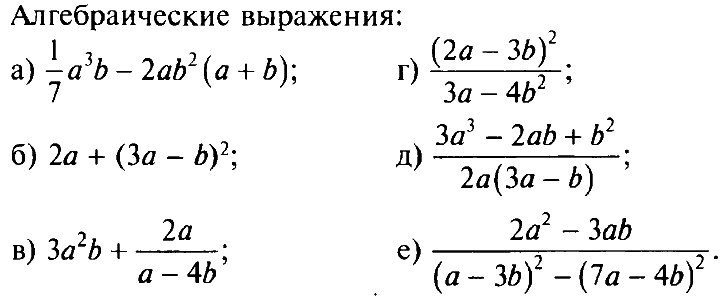
Алгебраическое выражение, которое не содержит деления на выражения с переменными, называется целым. В примере 1 целыми являются выражения а и б. Выражение, которое содержит деление на переменные, называется дробным. В примере 1 дробными являются выражения в—е. Целые и дробные выражения вместе называются рациональными. После преобразований целые выражения можно подразделить на одночлены и многочлены.

Пример 2

Рациональное выражение, представляющее собой дробь, числитель и знаменатель которой многочлены, называется рациональной дробью. При этом одночлены считаются частным видом многочленов.

Пример 3

а) Рациональные дроби:

б) Рациональные выражения

не являются рациональными дробями (по определению), так как в первых двух случаях выражения не являются дробью, в третьем случае числитель дроби будет многочленом только после преобразований, в четвертом случае знаменатель дроби станет многочленом также только после преобразований.

Разумеется, принципиальных отличий рационального выражения от рациональной дроби не существует. После соответствующих преобразований рациональное выражение можно привести к рациональной дроби. В примере 3, б в первом случае достаточно привести подобные члены, во втором случае привести выражения к общему знаменателю, в третьем случае числитель возвести в квадрат, в четвертом случае знаменатель возвести в куб.

2. Допустимые значения переменных в выражении

Значения переменных, при которых алгебраическое выражение имеет смысл, называются допустимыми значениями переменных. Целое выражение имеет смысл при любых значениях, входящих в него переменных, так как все действия с переменными выполнимы.

Пример 4

Пример 5

III. Задания на уроках

№ 2; 3; 4 (а); 5 (б); 7 (а); 9 (б); 10 (б); 12; 14; 15 (а); 17 (а); 18 (а, б); 19 (а).

IV. Контрольные вопросы

Какое выражение называется алгебраическим? Приведите примеры.
Дайте определение целого и дробного выражений. Приведите примеры.
Вспомните понятия одночлена и многочлена (курс 7 класса). Приведите примеры.
Какое выражение называется рациональной дробью? Приведите примеры.
Какие значения переменных называются допустимыми?
При каких значениях переменных целое выражение имеет смысл?
При каком условии дробное выражение не имеет смысла? Приведите примеры.

V. Подведение итогов уроков

Домашнее задание: № 1; 4 (б); 5 (а); 7 (б); 8 (а); 9 (а); 10 (а); 11; 13; 15 (г); 16(6, в); 17(6); 19 (б).

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). Глава 1. Рациональные дроби. § 1. Рациональные дроби и их свойства (5 ч). Уроки 1-2. Рациональные выражения. Вернуться к Списку уроков Тематического планирования.

Определение и примеры рациональных выражений

Для примера имеем, что 5 , 2 3 · x - 5 , - 3 · a · b 3 - 1 c 2 + 4 a 2 + b 2 1 + a : ( 1 - b ) , ( x + 1 ) · ( y - 2 ) x 5 - 5 · x · y · 2 - 1 11 · x 3 .

Основные виды преобразований рациональных выражений

Преобразовать рациональное выражение 3 · x x · y - 1 - 2 · x x · y - 1 .

3 · x x · y - 1 - 2 · x x · y - 1 = x x · y - 1 · 3 - 2 = x x · y - 1

Ответ: 3 · x x · y - 1 - 2 · x x · y - 1 = x x · y - 1 .

Выполнить преобразование 2 · x · y 4 · ( - 4 ) · x 2 : ( 3 · x - x ) .

2 · x · y 4 · ( - 4 ) · x 2 : 2 : x = ( 2 · ( - 4 ) : 2 ) · ( x · x 2 : x ) · y 4 = - 4 · x 2 · y 4

Ответ: 2 · x · y 4 · ( - 4 ) · x 2 : ( 3 · x - x ) = - 4 · x 2 · y 4 .

Преобразовать выражение вида x · ( x + 3 ) - ( 3 · x + 1 ) 1 2 · x · 4 + 2 .

Преобразуем в числителе формулу разности квадратов, тогда получаем, что

x 2 - 1 2 · x + 2 = ( x - 1 ) · ( x + 1 ) 2 · ( x + 1 ) = x - 1 2

Ответ: x · ( x + 3 ) - ( 3 · x + 1 ) 1 2 · x · 4 + 2 = x - 1 2 .

Представление в виде рациональной дроби

Представить в виде рациональной дроби a + 5 a · ( a - 3 ) - a 2 - 25 a + 3 · 1 a 2 + 5 · a .

Следует начать с умножения, тогда получим, что

a 2 - 25 a + 3 · 1 a 2 + 5 · a = a - 5 · ( a + 5 ) a + 3 · 1 a · ( a + 5 ) = a - 5 · ( a + 5 ) · 1 ( a + 3 ) · a · ( a + 5 ) = a - 5 ( a + 3 ) · a

Производим представление полученного результата с исходное. Получим, что

a + 5 a · ( a - 3 ) - a 2 - 25 a + 3 · 1 a 2 + 5 · a = a + 5 a · a - 3 - a - 5 a + 3 · a

Теперь выполняем вычитание:

После чего очевидно, что исходное выражение примет вид 16 a 2 - 9 .

Ответ: a + 5 a · ( a - 3 ) - a 2 - 25 a + 3 · 1 a 2 + 5 · a = 16 a 2 - 9 .

Представить x x + 1 + 1 2 · x - 1 1 + x в виде рациональной дроби.

Следует, что x x + 1 + 1 2 · x - 1 1 + x = 2 · x + 1 x + 1 2 · x - 1 1 + x

Получившаяся дробь может быть записана как 2 · x + 1 x + 1 : 2 · x - 1 1 + x .

После деления придем к рациональной дроби вида

2 · x + 1 x + 1 : 2 · x - 1 1 + x = 2 · x + 1 x + 1 · 1 + x 2 · x - 1 = 2 · x + 1 · ( 1 + x ) ( x + 1 ) · ( 2 · x - 1 ) = 2 · x + 1 2 · x - 1

Можно решить это иначе.

На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. А также узнаем, какие значения называют допустимыми, и научимся их находить.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Рациональные выражения"

На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.

Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Целые и дробные выражения называют рациональными выражениями.

Определение

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.

Дробное выражение при некоторых значениях переменных может не иметь смысла.

Чтобы найти значение рационального выражения, надо:

1) подставить числовое значение переменной в данное выражение;

2) выполнить все действия.

Определение

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.

Как вы уже знаете, выражение вида называется дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Найдите значение дроби.

Найдите допустимые значения переменной в выражениях:

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Чтобы найти значение рационального выражения, надо:

1) Подставить числовое значение переменной в данное выражение;

2) Выполнить все действия.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.

Читайте также: