Пространство в математике это кратко
Обновлено: 04.07.2024
Рассказывать школьникам о пространстве не как философской категории, а как о математическом понятии очень непросто. Об этом почти нет популярной литературы, а имеющиеся учебники адресованы студентам математических факультетов университетов. Я предлагаю свой рассказ о том, что такое пространство в математике.
Наверное, нужно начать с того, что пространство — очень объемное понятие, которому в разных контекстах придаются самые различные смыслы: вспомним хотя бы космическое, воздушное, межклеточное или информационное пространство. Конечно, разумно было бы начать с определения, однако пространство, как и любое другое основное понятие, является неопределяемым (аналогично число, множество, функция в алгебре, точка, прямая, плоскость в геометрии). Неопределяемые понятия мы можем только описывать, разъясняя, что имеется в виду, заменяя определяемое слово синонимами, обращаясь к интуиции и жизненному опыту.
Итак, под пространством понимают множество некоторых объектов, правила работы с ними и набор аксиом, которым эти правила должны подчиняться. Иными словами, это множество со введенной на нем структурой. По-разному определяя множество и структуру, мы получаем разные пространства. Из изучаемых школьном курсе можно отметить Евклидово пространство (одномерное, двумерное и трехмерное), линейное или векторное пространство и вероятностное пространство. Их элементами являются соответственно точки, векторы и элементарные события. Упоминается также четырехмерное пространство-время — пространство Минковского. (Заметим, что пространство Минковского не является четырехмерным Евклидовым пространством, поскольку имеет три пространственные и одну временную, но не пространственную, координату).
Одной из важнейших характеристик пространства является его размерность. С точки зрения аналитической геометрии, размерность фигуры равна числу координат, нужных для определения положения лежащей на этой фигуре точки; например, положение точки на кривой определяется одной координатой, на поверхности — двумя координатами, в трёхмерном пространстве — тремя координатами. (Необходимо отметить, что с середины 19 века геометрия стала изучать многомерные пространства, а в 20 веке — и пространства дробных размерностей).
Примером одномерного пространства является числовая прямая, положение каждой точки на ней можно характеризовать единственным числом. На прямой могут располагаться точки и отрезки (интервалы, полуинтервалы), они имеют одну пространственную характеристику — протяженность или длину. Примером двумерного пространства является плоскость, точки плоскости задаются двумя координатами. Плоские объекты характеризуются не только длиной, но и шириной. Примером трехмерного пространства является окружающий нас мир (Это утверждение верно до некоторых пределов. С точки зрения общей теории относительности, наш мир — искривляемое массивными телами четырехмерное пространство-время). Наряду с длиной и шириной появляется третье измерение, называемое высотой. Положение точек в трехмерном пространстве задается тремя пространственными координатами, в прямоугольной системе координат называемыми абсциссой, ординатой и аппликатой.
В рамках базовой школьной программы изучается только прямоугольная система координат. Однако необходимо отметить, что существуют и непрямоугольные системы координат, например, полярная и сферическая. В полярной системе координат на плоскости положение точки характеризуется двумя числами: расстоянием от точки до полюса и углом между полярной осью и отрезком, соединяющим точку с полюсом. Эта система координат удобна тем, что в ней уравнения некоторых линий принимают более простой вид, чем в прямоугольной системе координат. Аналогично, для задания положения точки на поверхности Земного шара понятия широты и долготы более удобны, чем какие-либо другие координаты. В сферической системе координат положение точки задают расстоянием от нее до начала координат, зенитным и азимутальным углами.
Конечно, наибольший интерес вызывает обсуждение многомерных гипертел. Приведем схему, позволяющую представить эволюцию геометрических объектов от точки до четырехмерного гиперкуба. Пусть у нас есть точка, которую мы сдвигаем вдоль прямой на некоторое расстояние. Если мы представим, что при движении точка оставляет след, то в результате сдвига мы получим отрезок. Будем теперь смещать отрезок в перпендикулярном ему направлении на расстояние, равное его длине. Результат построения — квадрат. Смещая теперь квадрат в перпендикулярном его плоскости направлению на расстояние, равное длине его стороны, получим куб. Рассуждая аналогично, мы можем вообразить четырехмерный гиперкуб. Он будет результатом смещения нашего трехмерного куба в направлении ему перпендикулярном на расстояние, равное длине любого из его ребер (см. рис. 1).
Больше того, наш алгоритм позволяет заметить геометрические характеристики гиперкуба! Проследим поэтапно: начальное и конечное положение движущейся точки обусловили наличие двух вершин отрезка. В свою очередь, четыре вершины квадрата образовались из двух вершин исходного и еще двух — смещенного отрезка. Число вершин куба представляет собой сумму числа вершин исходного и смещенного квадратов, поэтому их восемь, а число вершин гиперкуба будет равно шестнадцати — это вершины исходного и смещенного кубов. (Заметим, что число вершин 2, 4, 8, 16… является геометрической прогрессией.)
Далее, у нашего трехмерного куба 6 плоских граней — это исходный и смещенный квадраты, а также квадраты, полученные движением 4 сторон исходного квадрата. Аналогично число плоских граней гиперкуба — 24: по 6 граней у исходный и смещенного кубов, и еще 12, полученных движением 12 ребер исходного куба. Помимо 24 плоских граней, гиперкуб будет иметь еще 8 кубических граней: действительно, отрезок ограничен 2 точками, квадрат — 4 сторонами, куб — 6 гранями, гиперкуб — 8 кубами и т. д.; числа 2, 4, 6, 8… образуют арифметическую прогрессию. (Продолжая, мы можем рассматривать пятимерный гиперкуб. Он имеет 32 вершины, 80 ребер, 80 квадратных, 40 кубических и 10 гиперкубических граней. И так далее.)
При всей схожести построения объектов, пространства, в которых они существуют совсем разные.
Рассмотрим мир жителей прямой. Вне прямой для них ничего не существует, просто ничего нет, даже пустоты. Внутри этого мира органами зрения можно видеть лишь точки. Это сами точки, или перпендикулярные проекции отрезков (представьте, что мы смотрим на иголку со стороны острия). Движение возможно только между двумя объектами на прямой, так как обойти точки, не сходя с этой нее, невозможно (см. рис. 2).
Двумерный мир представляет собой плоскость. Обитатели этого мира — точки, отрезки, плоские фигуры. Глядя друг на друга, они могут видеть лишь отрезки, которыми являются проекции плоских фигур на прямую (см. рис. 3).
Трехмерный мир окружает нас. Мы привыкли к нему, объекты, окружающие нас трехмерны, хоть в каждый момент времени мы видим только их плоские проекции — как на фотографии. Если бы мы были четырехмерными, в трехмерном мире перед нами открылись самые фантастические возможности.
Итак, из следующего измерения мы получаем возможность видеть насквозь все, происходящее в пространстве меньшей размерности, возможность беспрепятственно перемещать предметы сквозь границы, видоизменяться в пространствах меньшей размерности, появляясь в них тем или иным своим многомерным сечением, исчезать в одной точке и появляться в другой точке беспричинно и непредсказуемо для обитателей меньших размерностей. В этом, несмотря на всю непохожесть, наши пространства имеют много общего.
Сила и красота математики, ее абстрактность и универсальность состоят как раз в том, что она находит универсальные единые методы описания пространств, что используемый язык позволяет строить плодотворные модели и аналогии для самых непохожих на первый взгляд объектов.
- логически мыслимая форма (или структура), служащая средой, в к-рой осуществляются другие формы и те или иные конструкции. Напр., в элементарной геометрии плоскость или пространство служат средой, где строятся разнообразные фигуры. В большинстве случаев в П. фиксируются отношения, сходные по формальным свойствам с обычными пространственными отношениями (расстояние между точками, равенство фигур и др.), так что о таких П. можно сказать, что они представляют логически мыслимые пространственно-подобные формы. Первым и важнейшим математич. П. является трехмерное евклидово пространство, представляющее приближенный абстрактный образ реального П. Общее понятие "П." в математике сложилось в результате обобщения и видоизменения понятий геометрии евклидова П. Первые П., отличные от трехмерного евклидова, были введены в 1-й пол. 19 в. Это были Лобачевского пространство и евклидово П. любого числа измерений (см. Многомерная геометрия). Общее понятие о математич. П. как "многократной протяженности" было выдвинуто в 1854 Б. Риманом (В. Riemann); оно обобщалось, уточнялось и конкретизировалось в разных направлениях: таковы, напр., риманово пространство, финслерово пространство, векторное пространство, гильбертово пространство, метрическое пространство, топологическое пространство. В современной математике П. определяют как множество каких-либо объектов, к-рые наз. его точками; ими могут быть геометрич. фигуры, функции, состояния физич. системы и т. д. Рассматривая их множество как П., отвлекаются от всяких их свойств и учитывают только те свойства их совокупности, к-рые определяются принятыми во внимание или введенными по определению отношениями. Эти отношения между точками и теми или иными фигурами, т. е. множествами точек, определяют "геометрию" П. При аксиоматич. ее построении основные свойства этих отношений выражаются в соответствующих аксиомах.
Примерами П. могут служить: 1) метрич. П., в к-рых определено расстояние между точками; напр., П. непрерывных функций на к.-л. отрезке [a, b], где точками служат функции f(x), непрерывные на [ а, b], а расстояние между f 1 (x). и f 2 (x) определяется как максимум модуля их разности:
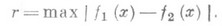
2) "П. событий", играющее важную роль в геометрич. интерпретации теории относительности. Каждое событие характеризуется положением - координатами х, у, z и временем t, поэтому множество всевозможных событий оказывается четырехмерным П., где "точка" - событие определяется 4 координатами х, у, z, t.3) Фазовые П., рассматриваемые в теоретич. физике и механике. Фазовое П. физич. системы - это совокупность всех ее возможных состояний, к-рые рассматриваются при этом как точки этого П. А.
Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .
Полезное
Смотреть что такое "ПРОСТРАНСТВО" в других словарях:
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неоднородность. Множество предметов, объектов, данных в человеческом восприятии одновременно, формирует сложный… … Философская энциклопедия
ПРОСТРАНСТВО — П., будучи одним из важнейших элементов мифопоэтической архаичной модели мира, осмысливалось в рамках этой модели совершенно отлично от того, как оно представляется современному человечеству под воздействием научных взглядов (особенно после… … Энциклопедия мифологии
Пространство — Пространство ♦ Espace То, что остается, если убрать все; пустота, но пустота в трех измерениях. Ясно, что понятие пространства – абстракция (если мы действительно уберем все, то не останется вообще ничего, и это будет уже не пространство, а… … Философский словарь Спонвиля
ПРОСТРАНСТВО — в математике множество объектов, между которыми установлены отношения, сходные по своей структуре с обычными пространственными отношениями типа окрестности, расстояния и т. д. Исторически первое и важнейшее математическое пространство евклидово… … Большой Энциклопедический словарь
пространство — См. промежуток. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. пространство место, промежуток; площадь, участок, зона, район, область; окно, протяженность, прогалина, гаммада,… … Словарь синонимов
пространство — ПРОСТРАНСТВО фундаментальное понятие повседневной жизни и научного знания. Его обычное применение непроблематично в отличие от его теоретической экспликации, поскольку последнее связано с множеством других понятий и предполагает… … Энциклопедия эпистемологии и философии науки
ПРОСТРАНСТВО — ПРОСТРАНСТВО, объективная реальность, форма существования материи, характеризующаяся протяженностью и объемом. В реальном мире мы имеем дело с безграничным трехмерным пространством, в котором расположены объекты. В математике пространством… … Научно-технический энциклопедический словарь
пространство — пространство: восприятие восприятие пространства пространство: восприятие: нарушение … Большая психологическая энциклопедия
ПРОСТРАНСТВО — культуры важнейший аспект модели мира, характеристика протяженности, структурности, сосуществования, взаимодействия, координации элементов отд. культуры и соответствующих отношений между культурами, а также смысловой… … Энциклопедия культурологии
ПРОСТРАНСТВО — ПРОСТРАНСТВО, пространства, ср. 1. Состояние материи, характеризующееся наличием протяженности и объема. Пространство и время основные формы существования материи. 2. Промежуток между чем нибудь; место, способное вместить что нибудь. Свободное… … Толковый словарь Ушакова

Сударев Ю. Н. Понятие пространства в математике. — М. : Знание, 1974. — 64 с. — (Новое в жизни, науке, технике. Математика, кибернетика ; 12/1974). — Библиогр.: с. 61 (18 назв.).
Обложка 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
Если строка в кавычках ". ", то найдутся страницы со словосочетанием в точно такой форме.
По вашему запросу ничего не найдено.
Убедитесь, что слова написаны без ошибок или попробуйте выбрать другие значения.

Многомерные пространства — миф или реальность? Большинству из нас, или, возможно, всем нам невозможно представить мир, состоящий из более чем трех пространственных измерений. Правильно ли утверждение, что такой мир не может существовать? Или просто человеческий разум не способен вообразить дополнительные измерения — измерения, которые могут оказаться такими же реальными, как и другие вещи, которые мы не можем увидеть?
Об авторах
Илья Щуров — кандидат физико-математических наук, доцент кафедры высшей математики НИУ ВШЭ.
Jason Hise — Physics programmer at Ready at Dawn Studios, 4D geometry enthusiast. Автор анимированных моделей, представленных в данной статье.
ashgrowen — пикабушник, проиллюстрировавший в этой статье построение тессеракта и гиперкуба.
Давайте начнем с простого — начнем с одномерного пространства. Представим себе, что у нас есть город, который расположен вдоль дороги, и в этом городе есть только одна улица. Тогда мы можем каждый дом на этой улице закодировать одним числом — у дома есть номер, и этот номер однозначно определяет, какой дом имеется в виду. Люди, которые живут в таком городе, — можно считать, что они живут в таком одномерном пространстве. Жить в одномерном пространстве довольно скучно, и люди обычно живут не в одномерном пространстве.
Вопрос: что такое четырехмерное пространство? Представить его себе не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время. Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.
Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке. Можно представлять себе, хотя это уже совсем сложно, пространство большей размерности. На самом деле математики, когда работают с пространствами высокой размерности, чаще всего говорят просто: допустим, пятимерное пространство — это пространство, в котором точка задается пятью числами, пятью координатами. Безусловно, математики разработали разные методы, которые позволяют понимать что-то о геометрии такого пространства.
Почему это важно? Зачем понадобились такие пространства? Во-первых, четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое. Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать.
В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.
Для того чтобы изучать такие объекты, используются методы, разработанные в науке, которая называется линейная алгебра. Несмотря на то, что она алгебра, на самом деле это наука о геометрии многомерных пространств. Конечно, поскольку представить их себе довольно тяжело, математики используют формулы, для того чтобы как раз изучать такие пространства.
Представить себе четырех-, пяти- или шестимерное пространство довольно сложно, но математики не боятся трудностей, и им мало даже стомерных пространств. Математики придумали бесконечномерное пространство — пространство, содержащее бесконечное количество измерений. В качестве примера такого пространства можно привести пространство всех возможных функций, заданных на отрезке или прямой.
Оказывается, что методы, которые были разработаны для конечномерных пространств, во многом переносятся и на случаи чрезвычайно сложных с точки зрения просто попытки их все представить пространств.
У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.
Со школьных лет математика разделяется на алгебру и геометрию. Но на самом деле, если мы задумаемся о том, как устроена современная математика, то мы поймем, что те задачи, которые сейчас решаются, в частности, с применением методов линейной алгебры, на самом деле являются очень отдаленным продолжением тех задач, над которыми задумывались многие тысячи лет назад, например Пифагор или Евклид, разрабатывая ту самую школьную геометрию, которая сейчас есть в любом школьном учебнике. Удивительно, что задача по анализу больших данных оказывается в некотором смысле потомком, казалось бы, совсем бессмысленных — по крайней мере с практической точки зрения — упражнений древних греков по рисованию прямых или окружностей на плоскости или мысленному проведению прямых или плоскостей в трехмерном пространстве.
Тессерракт — четырехмерный куб
Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.
Тессеракт — четырехмерный куб
Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.).
Тессеракт — четырехмерный куб
На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.
Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.
Представление других измерений

От 2D к 3D
Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.
Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.

Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.
Принимая во внимание исключительность как жанра, который при некоторой фантазии и существовании иных его представителей, можно было бы назвать математическим романом, так и самой книги, её не хочется сильно ругать. Тем не менее, похвалы здесь заслуживает только лишь непривычность подачи, по духу близкая произведениям Льюиса Керрола, однако, в отличие от него, имеющая гораздо меньше точек соприкосновения с реальной жизнью. Данная книга, как верно отмечено в предисловии к изданию, не похожа ни на одну популяризацию, читателю, однако, не вполне ясно, по какой причине её сравнивают с популяризациями, потому как, хотя математические истины в ней, безусловно, затрагиваются, какой бы то ни было популяризацией книгу определённо считать невозможно. И вот почему: Перед вами уникальный пример объединения художественного вымысла с математическими идеями. И поклоннику математики, любящему читать, задумка изначально кажется замечательной: подобно математическим постулатам, ввести в рассмотрение ряд абстрактных объектов, наделить их определёнными свойствами, задать правила игры в описанном пространстве, а после, подражая опять же мысли исследователя, наблюдающего взаимодействия этих умозрительных объектов, проследить за их трансформацией. Но, так как книга всё же художественная, усилиям воли учёного места здесь не находится, поэтому для самодостаточности представленного на всеобщее обозрение мира объекты здесь наделяются сознанием и мотивацией для каких-либо взаимодействий друг с другом, после чего в прежде абстрактный мир оторванных от повседневной жизни чистых идей приносятся социальные взаимодействия с целым ворохом проблем, всегда сопутствующих всяким взаимоотношениям. Всевозможные трения, возникающие в книге на социальной почве, по мнению зрителя совершенно не нужны в книге: они практически не раскрыты и не могут восприниматься в серьезе, и в то же время отвлекают читателя от истинно тех вещей, ради которых написана книга. Даже принимая во внимания заверения обоих авторов о неспешности повествования, якобы более комфортную для читателя при приобретении каких-либо знаний (именно здесь приводится сравнение с популяризациями), зрителю темп повествования показался чрезвычайно затянутым и медлительным, а повторение одного и того же объяснения по несколько раз одними и теми же словами заставило усомниться в том, что рассказчик адекватно оценивает его умственным способности. И в конечном счёте неясно, для кого эта книга. Непривычным к математике людям описание в общем-то интересных явление в столь вольной форме вряд ли принесёт удовольствие, знакомым же с математикой ближе будет гораздо приятнее взять в руки качественную популяризацию, где величие и красоту математики не разбавляют плоскими сказками.
От 3D к 4D
Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.
Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..
Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.
Читайте также:

