Применение теоремы пифагора в архитектуре кратко
Обновлено: 02.07.2024
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Презентация т.Пифагора Байтурина2.pptx
Описание презентации по отдельным слайдам:

Выяснить области применения теоремы Пифагора в строительстве и архитектуре Цель работы:

Задачи: Изучить некоторые исторические сведения о Пифагоре и о его теореме. Рассмотреть различные доказательства теоремы Пифагора. Собрать информацию о практическом применении теоремы. Пифагора из различных источников и определить области применения теоремы в строительстве и архитектуре. Обработать собранные данные, подобрать иллюстрации. Оформить наработанный материал в виде проекта.

Немного о Пифагоре Пифагор -древнегреческий учёный VI в. до н. э. Сохранилось предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков.

Теорема Пифагора Знаменитая теорема Пифагора читается так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

1. Как называется самая известная теорема геометрии? 2. Можете ли вы её сформулировать?

Построение прямого угла с помощью верёвки

Построение окна в готическом и романском стилях

Собор Парижской Богоматери

Строительство двускатной крыши a= 2м b= 6:2= 3м с=√2²+3² ≈ 3,6м


Спасибо за внимание !
Выбранный для просмотра документ Применение теоремы Пифагора.docx
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИ И
федеральное государственное АВТОНОМНОЕ образовательное учреждение высшего образовани я
Озерский технологический институт –
(ОТИ НИЯУ МИФИ)
Специальность 08.02.01 Строительство и эксплуатация зданий и сооружений
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
Разработали ________________/ О. Д. Байтурина /
подпись инициалы, фамилия
______________________ / В. Д. Сиринова /
Руководитель проекта _____________/ Н.П. Лазарева /
подпись инициалы, фамилия
ЦЕЛЬ проекта: выяснить области применения теоремы Пифагора в строительстве и архитектуре.
Изучить некоторые исторические сведения о Пифагоре и о его теореме.
Рассмотреть различные доказательства теоремы Пифагора.
Собрать информацию о практическом применении теоремы Пифагора из различных источников и определить области применения теоремы в строительстве и архитектуре.
Обработать собранные данные, подобрать иллюстрации.
Оформить наработанный материал в виде проекта.
Защитить творческий проект.
Руководитель индивидуального проекта _____________ / Н. П. Лазарева /
Задание получили ______________________ / О. Д. Байтурина /
______________________ / В. Д. Сиринова /
1 Применение теоремы Пифагора в строительстве и архитектуре………………. 6
1.3 Применение теоремы Пифагора …………………………. 9
1.3.1 Теорема Пифагора при построении прямых углов на местности…………. 9
1.3.2 Построение окна в готическом и романском стилях………………10-11,16-17
Список использованной литературы ……………………………………. 14
Целью нашей работы было: выяснить области применения теоремы Пифагора в строительстве и архитектуре.
Таким образом, исследовав литературные источники, мы не нашли в них ответа на вопрос о практическом применении теоремы Пифагора. Изучить этот вопрос нам помогли только материалы в интернете.
Нам было интересно, знают ли теорему Пифагора студенты, учителя, родители? Чтобы выяснить это, мы провели анкетирование и обработали результаты. Было опрошено 27 студентов, 14 преподавателей и 15 родителей (приложение №1).
1 Применение теоремы Пифагора в строительстве и архитектуре
1.1 Немного о Пифагоре
Крепкого телосложения юношу судьи одной из первых в истории Олимпиад не хотели допускать к спортивным состязаниям, так как он не вышел ростом. Но он не только стал участником Олимпиады, но и победил всех противников. Такова легенда. Этот юноша был Пифагор - знаменитый математик. Вся его жизнь – легенда, точнее наслоение многих легенд. Он родился на острове Самос, у берегов Малой Азии. Всего 5 километров водной глади отделяло этот остров от большой земли. Совсем юным Пифагор покинул родину. Он прошел по дорогам Египта, 12 лет жил в Вавилоне, где слушал речи жрецов, открывавших перед ним тайны астрономии и астрологии, затем несколько лет – в Италии. Уже в зрелом возрасте Пифагор переселяется в Сицилию и там, в Кротоне, создает удивительную школу, которую назовут пифагорейской. Они были трудолюбивы и аскетичны – Пифагор и его ученики. Вот заповеди пифагорейцев:
Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
Не делай никогда того, чего не знаешь, но научись всему, что следует знать.
Не пренебрегай здоровьем своего тела.
Приучайся жить просто и без роскоши.
Прежде чем лечь спать, проанализируй свои поступки за день.
Трудно сказать, какие научные идеи принадлежали Пифагору, какие – его воспитанникам. Но рассказывают, что Пифагор, доказав свою знаменитую теорему, отблагодарил богов, принеся им в жертву 100 быков. Пифагор не записал своего учения. Оно известно лишь в пересказах Аристотеля и Платона. Греческий ученый Гераклит утверждал, что Пифагор ученее всех современников, однако порицал его за склонность к магии. Дело в том, что числа для пифагорейцев были наполнены магическим содержанием, они преклонялись перед гармонией чисел. Пифагор был не только математиком, но и философом. Ему принадлежит немало великих догадок. Вот почему люди помнят его уже две с половиной тысячи лет, а среди знаменитых олимпийских чемпионов Пифагор наиболее знаменит, - ему выпало счастье победить не только соперника, но и время.
1.2 Теорема Пифагора
Теорема Пифагора доказана более чем 100 способами. Мы познакомились с тремя способами доказательства теоремы. Приведём наиболее простое геометрическое доказательство этой теоремы: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c
(рис. 1). Нарисуем два квадрата, стороны которых равны ( a + b ) – сумме двух катетов прямоугольного треугольника. Затем в полученных квадратах выполним построения (рис.2, рис.3).

Все зарисованные на рис. 2 и 3 фигуры – квадраты со сторонами, равными катетам и гипотенузе прямоугольного треугольника. Очевидно, что сумма площадей зарисованных квадратов на рис.2 () равна площади зарисованного квадрата на рис.3 (, а именно: площади квадрата со стороной ( a + b ) за вычетом четырех площадей равных между собой треугольников.
Итак, теорема Пифагора доказана.
Приведём ещё два доказательства теоремы.

Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c
(рис. 4). Докажем, что
Достроим треугольник до квадрата со стороной a + b так, как показано на
рисунке (рис. 5). Площадь S этого квадрата равна . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна , и квадрата со стороной c , поэтому
S = . Таким образом, , откуда
Интересно доказательство Перигаля теоремы Пифагора. Данное доказательство основано на разрезании квадратов, построенных на катетах
(рис. 6), и укладывании полученных частей на квадрате, построенном на гипотенузе. В учебниках нередко встречается разложение, указанное на рисунке (так называемое "колесо с лопастями"; это доказательство нашел Перигаль ). Через центр квадрата, построенного на большем катете, проводим прямые, параллельные и перпендикулярные гипотенузе. Соответствие частей фигуры хорошо видно из чертежа.
Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах,
написанных за 1200 лет до Пифагора. Она была известна в Китае и Индии. Одно из древнейших доказательств теоремы Пифагора, очень громоздкое и трудное, дано Евклидом. О прямоугольном треугольнике со сторонами 3, 4, 5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим.
1.3 Применение теоремы Пифагора
1.3.1 Теорема Пифагора при построении прямых углов на местности
Очень легко можно воспроизвести способ построения прямых углов "натягиванием веревок". Возьмем веревку и сделаем на ней метки, делящие её
на 12 равных частей. Свяжем её концы и растянем верёвку на земле с помощью кольев в виде треугольника со сторонами, равными 3, 4 и 5. Тогда прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра ( рис.7).

Рис. 7
1.3.2 Построение окна в готическом и романском стилях
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон (приложение №2). На рисунке (рис. 8) представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2) для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг.
Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.
В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный (приложение №3). На рисунке (рис.9), если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой
b /2- p . По теореме Пифагора имеем: ( b /4+ p ) 2 =( b /4) 2 +( b /2- p ) 2 или b 2 /16+ bp /2+ p 2 = b 2 /16+ b 2 /4- bp + p 2 , откуда bp /2= b 2 /4 - bp . Разделив на b и приводя подобные члены, получим: (3/2)p=b/4, p=b/6.
1.3.3 Строительство крыши
При строительстве домов и коттеджей часто встает вопрос о длине стропил для двускатной крыши (приложение 4). Например: ширина здания 6 м, высота предполагаемой крыши 2 м (рис. 10). Какой длины должны быть стропила?
Решение: В прямоугольном треугольнике длина одного катета – a = 2 м
(ширина здания), длина второго катета – b = 6:2 = 3 (м). По теореме Пифагора находим гипотенузу (длина стропил): c =

Взяв за основу эту задачу, мы решили исследовать двускатную крышу и проверить, выполняется ли для неё теорема Пифагора. Проведя измерения крыши, получили следующие результаты: длина балки – 12,2 м., высота – 3 м., длина стропила – 6,8 м.
Двускатная крыша в сечении – равнобедренный треугольник, тогда длину стропила вычислим по теореме Пифагора: ≈ 6,8 (м). Учитывая погрешность измерения, приходим к выводу, что рабочие при строительстве крыши пользовались известной теоремой.

Бесплатное участие. Свидетельство СМИ сразу.
До 500 000 руб. ежемесячно и 10 документов.
Применение теоремы Пифагора В архитектуре. В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. В строительстве. Возможно, кто-то сочтет приложения теоремы Пифагора сугубо теоретическими. Но это не так. Если, например, рассматривать треугольную призму как крышу башни, то в первом вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши. В физике. Молниеотвод, громоотвод – устройство для защиты зданий, промышленных, транспортных, коммунальных, сельскохозяйственных и других сооружений от ударов молнии.

Теорема Пифагора – самая известная теорема геометрии, о ней знает подавляющее большинство населения планеты. Математики тысячелетиями говорят о ее величественности и значимости. Ей посвящены легенды, стихи. Меня заинтересовало, настолько ли она величественна для моих ровесников. Я решила доказать, что теорема Пифагора актуальна и в наши дни.

«Практическое применение
Исследовательская работа по математике
Из истории создания теоремы Пифагора. 7
Опрос учащихся. 9
Практическое применение Теоремы Пифагора
Области применения теоремы Пифагора…………………………………. 11
Теорема Пифагора – самая известная теорема геометрии, о ней знает подавляющее большинство населения планеты. Математики тысячелетиями говорят о ее величественности и значимости. Ей посвящены легенды, стихи. Меня заинтересовало, настолько ли она величественна для моих ровесников. Я решила доказать, что теорема Пифагора актуальна и в наши дни.
Объектом исследования является теорема Пифагора.
Предмет исследования: практическое применение теоремы Пифагора.
Гипотеза исследования: если учащиеся поймут практическую значимость теоремы Пифагора, то они смогут применять ее при решении жизненных задач
Цель: доказать, что теорема Пифагора актуальна и в наши дни
Исходя из этой цели, мною были поставлены следующие задачи:
Изучить некоторые исторические сведения о Пифагоре и его теореме;
Собрать информацию о практическом применении теоремы в различных источниках и определить области ее применения;
Показать применение теоремы Пифагора при решении задач;
Оформить наработанный материал.
Проанализировать все результаты и сделать выводы.
Методы исследования: изучение научной литературы, опрос, анализ, сравнение, обобщение.
Историческая справка

1. Из биографии Пифагора
Пифагор Самосский – великий греческий учёный. Его имя знакомо каждому школьнику. Если попросят назвать одного древнего математика, то абсолютное большинство назовёт Пифагора. Про жизнь Пифагора достоверно почти ничего не известно, но с его именем связано большое количество легенд.
Пифагор имел красивую внешность, носил длинную бороду. Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".)
Среди учителей юного Пифагора были старец Гермодамант и Ферекид Сиросский. Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера.
Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя.
В 550 году до н. э Пифагор принимает решение и отправляется в Египет. Итак, перед Пифагором открывается неизвестная страна и неведомая культура. Многое поражало и удивляло Пифагора в этой стране, и после некоторых наблюдений за жизнью египтян Пифагор понял, что путь к знаниям, охраняемым кастой жрецов, лежит через религию.

П осле одиннадцати лет обучения в Египте Пифагор отправляется на родину, где по пути попадает в Вавилонский плен. Там он знакомится с вавилонской наукой, которая была более развита, чем египетская. Вавилоняне умели решать линейные, квадратные и некоторые виды кубических уравнений. Они успешно применяли теорему Пифагора более чем за 1000 лет до Пифагора. Сбежав из плена, он не смог долго оставаться на родине из-за царившей там атмосферы насилия и тирании. Он решил переселиться в Кротон (греческая колония на севере Италии).
Именно в Кротоне начинается самый славный период в жизни Пифагора. Там он учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни.
2. Пифагор и пифагорейцы

П ифагор организовал в греческой колонии на юге Апенинского полуострова религиозно-этическое братство, типа монашеского ордена, который впоследствии назовут пифагорейским союзом. Члены союза должны были придерживаться определённых принципов: во-первых, стремиться к прекрасному и славному, во-вторых, быть полезными, в-третьих, стремиться к высокому наслаждению.
Пифагорейская система занятий состояла из трёх разделов:
учения о числах – арифметике,
учения о фигурах – геометрии,
учения о строении Вселенной – астрономии.
Система образования, заложенная Пифагором, просуществовала много веков.
Пифагорейцы учили, что Бог положил числа в основу мирового порядка. Бог – это единство, а мир – множество и состоит из противоположностей. То, что приводит противоположности к единству и соединяет всё в космос, есть гармония. Гармония является божественной и заключается в числовых выражениях. Кто до конца изучит гармонию, сам станет божественным и бессмертным.

Музыка, гармония и числа были неразрывно связаны в учении пифагорейцев. Математика и числовая мистика были фантастически перемешаны в нём. Пифагор считал, что число есть сущность всех вещей и что Вселенная представляет собой гармоническую систему чисел и их отношений.
Школа Пифагора много сделала, чтобы придать геометрии характер науки. Основной особенностью метода Пифагора было объединение геометрии с арифметикой.
Пифагор много занимался пропорциями и прогрессиями и, вероятно, подобием фигур, так как ему приписывают решение задачи: "По данным двум фигурам построить третью, равновеликую одной из данных и подобную второй".
Пифагор и его ученики ввели понятие о многоугольных, дружественных, совершенных числах и изучали их свойства. Арифметика как практика вычислений не интересовала Пифагора, и он с гордостью заявил, что "поставил арифметику выше интересов торговца".
Пифагор одним из первых считал, что Земля имеет форму шара и является центром Вселенной, что Солнце, Луна и планеты имеют собственное движение, отличное от суточного движения неподвижных звезд.
Учение пифагорейцев о движении Земли Николай Коперник воспринял как предысторию своего гелиоцентрического учения. Недаром церковь объявила систему Коперника "ложным пифагорейским учением".
В школе Пифагора открытия учеников приписывались учителю, поэтому практически невозможно определить, что сделал сам Пифагор, а что его ученики.
Членами пифагорейского союза были жители многих городов Греции.
В своё общество пифагорейцы принимали и женщин. Союз процветал более двадцати лет, а потом начались гонения на его членов, многие из учеников были убиты.
О смерти самого Пифагора ходило много самых разных легенд. Но учение Пифагора и его учеников продолжало жить.
3. Из истории создания теоремы Пифагора
В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что именно Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду.

И сторический обзор теоремы Пифагора начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого.
Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора, гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше было известно о теореме Пифагора вавилонянам. В одном тексте, относимом ко времени Хаммураби, т.е. к 2000 году до нашей эры, приводится приближенное вычисление гипотенузы прямоугольного треугольника; отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.
Геометрия у индусов была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 8 века до нашей эры. Наряду с чисто ритуальными предписаниями, существуют и сочинения геометрически теологического характера, называемые Сульвасутры. В этих сочинениях, относящихся к 4 или 5 веку до нашей эры, мы встречаемся с построением прямого угла при помощи треугольника со сторонами 15, 36, 39.
В средние века теорема Пифагора определяла границу, если не наибольших возможных, то, по крайней мере, хороших математических знаний. Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора или человека в цилиндре, в те времена нередко употреблялся как символ математики.




Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
Евклида эта теорема гласит (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннариции (около 900 года до нашей эры), сделанный Герхардом Кремонским (12 век) гласит (в переводе):
В Geometry Culmonensis (около 1400года) теорема читается так (в переводе):
“Итак, площадь квадрата, измеренного по длиной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу”
Как видим, в разных странах и разных языках существуют различные варианты формулировки знакомой нам теоремы. Созданные в разное время и в разных языках, они отражают суть одной математической закономерности, доказательство которой также имеет несколько вариантов.
4. Пифагоровы тройки.
Поскольку уравнение x 2 + y 2 = z 2 однородно, при домножении x, y и z на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом, то есть x,y,z — взаимно простые числа. Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 (3 2 + 4 2 = 5 2 ).
Некоторые Пифагоровы тройки:
(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 35, 45), (14, 48, 50), (30, 40, 50)…
Пифагоровы тройки имеют важное значение в геометрии. Несмотря на то, что в школе на изучение Пифагоровых троек не отводится много времени, в настоящее время знание их необходимо при решении многих математических задач.
Опрос учащихся
- Знаешь ли ты теорему Пифагора? Ответы распределились следующим образом:

В процессе работы над индивидуальным проектом по математике "Теорема Пифагора" учеником 9 класса гимназии была поставлена и реализована цель рассмотреть практическое применения теоремы Пифагора в разных сферах деятельности человека и областях науки, помимо математики.
Подробнее о проекте:
В ученической исследовательской работе по математике "Теорема Пифагора" автор проводит анализ учебно-методической литературы и находит интересные сведения о Пифагоре. Также в проекте представлена правильная формулировка Теоремы Пифагора, приведено доказательство теоремы и представлены знаменитые философские высказывания Пифагора.
В готовом творческом и исследовательском проекте по математике "Теорема Пифагора" учащимся дано доказательство теоремы Пифагора через подобные треугольники, а также рассмотрено применение теоремы Пифагора в строительстве, в мобильной связи, в астрономии и в литературе. Школьник рассуждает над актуальностью применения теоремы Пифагора в повседневной жизни человека.
Оглавление
Введение
1. Это интересно знать.
2. Формулировка теоремы Пифагора.
3. Доказательство теоремы.
4. Философские высказывания Пифагора.
5. Доказательство теоремы Пифагора через подобные треугольники.
6. Применение теоремы Пифагора. Строительство.
7. Мобильная связь.
8. Астрономия.
9. Литература.
10. Применение теоремы Пифагора.
Выводы и заключение
Список литературы
Введение
На уроках геометрии мы познакомились с одной из важнейших теорем геометрии для прямоугольного треугольника, известной с древних времен – теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Кратко познакомились с историей этой теоремы, рассмотрели одно из ее доказательств, также узнали, что существуют и другие способы доказательства.
Причина такой популярности теоремы Пифагора очевидна: простота, красота и широкая значимость. Однако теорема Пифагора проста, но не так очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Кроме этого, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций. Зная теорему Пифагора, можно находить ее новые применения и способы доказательств.
С одной стороны – теорема Пифагора изучается и доказывается в школьном курсе геометрии, а с другой стороны - школьного материала явно недостаточно для того, чтобы показать ее практическую значимость в различных, в том числе и современных сферах деятельности человека.
Цель работы: Изучение практического применения теоремы Пифагора.
- Изучение биографии Пифагора.
- Изучение истории появления и развития теоремы Пифагора.
- Рассмотрение доказательства теоремы Пифагора.
- Подобрать интересные задачи, решаемые с помощью теоремы Пифагора.
Основные методы исследования: Метод исследования, систематизации и обработки данных.
Гипотеза: если теорема Пифагора так популярна и сегодня, то в ней заложены такие основы, которые позволяют использовать ее в различных, в том числе и современных сферах деятельности человека.
Объект исследования: практическое применение теоремы Пифагора в современной деятельности человека.
Предмет исследования: теорема Пифагора.
Это интересно знать
В течение 22 лет он проходил обучение в храмах Мемфиса и получил посвящение высшей степени. Здесь же он глубоко изучил математику, науку чисел или всемирных принципов, из которой впоследствии сделал центр своей системы. Кроме того, что Пифагор был математиком, он также имел отношение к литературе и философии.
Пифагора можно отнести и к великим мыслителям своего времени. Одна из самых главных заслуг Пифагора-это доказательство теоремы, которая носит его имя. Существует около 500 способов её доказательства, и это одна из теорем, которая доказывает большую часть математических теорем.
Формулировка теоремы Пифагора
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника:
Сумма квадратов длин катетов равна квадрату длины гипотенузы.a²+b²=c²
Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике. Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора.
Квадраты, построенные на катетах, состоят из 2-х одинаковых треугольников. А квадрат, построенный на гипотенузе, состоит из 4-х таких треугольников. Вероятно, факт, изложенный в теореме Пифагора, сначала был дан для равнобедренных треугольников. Таким образом, площадь квадрата построенного на стороне С, равна сумме площадей квадратов, построенных на сторонах А и В.
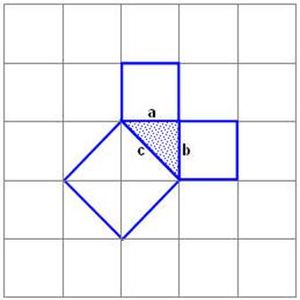
Доказательство теоремы
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. И в этом случае так же площадь квадрата построенного на гипотенузе С, будет равна сумме площадей квадратов, построенных на сторонах А и В.
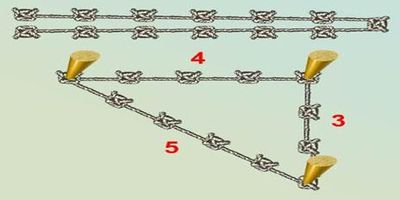
Задача
Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5. Правильно ли они поступали?
Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
Философские высказывания Пифагора
- Делай лишь то, что впоследствии не огорчит тебя и не заставит раскаиваться.
- Статуя формой своей хороша, а человека украсят дела.
- Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает.
Доказательство теоремы Пифагора через подобные треугольники
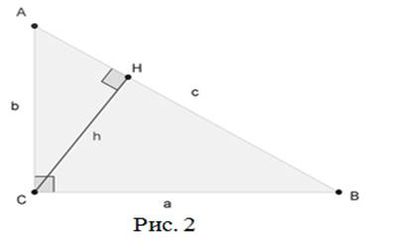
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H.
Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам (∠ACB=∠CHA=90%, ∠A- общий). Аналогично, треугольник CBH подобен ABC.
из подобия треугольников получаем, что
Отсюда имеем, что
Сложив полученные равенства, получаем
Что и требовалось доказать.
Применение теоремы Пифагора. Строительство
Задача 1
От столба высотой 9 м к дому натянут провод, который крепится на высоте
3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.

Решение задачи

Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD - прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD.
По теореме Пифагора
Задача 2
Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
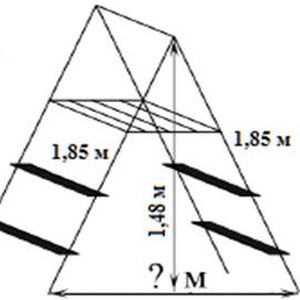
Решение задачи
Данная задача сводится к нахождению катета прямоугольного треугольника. Пусть х — искомое расстояние, тогда:
Задача 3
Девочка прошла от дома по направлению на запад 880 м. Затем повернула на север и прошла 900 м. После этого она повернула на восток и прошла ещё 400 м. На каком расстоянии (в метрах) от дома оказалась девочка?
Решение задачи
Восток и запад — противоположные направления, поэтому девочка прошла 880 − 400 = 480 м на запад. Пусть — гипотенуза прямоугольного треугольника. По теореме Пифагора, гипотенуза ищется следующим образом:
Мобильная связь
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
Решение задачи
Пусть AB=x, BC=R=200 км, OC=r=6380 км.
Используя теорему Пифагора, получим 23 км
Астрономия
Задача 6
На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой. Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?
Решение задачи
На этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью. Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается, и луч возвращается уже в новую точку C.
Вконце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Литература
Теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:
Свет истины рассеется не скоро,
Но, воссияв, рассеется навряд
И, как тысячелетия назад,
Не вызовет сомнения и спора.
Мудрейшие, когда коснется взора
Свет истины, богов благодарят;
И сто быков, заколоты, лежат –
Ответный дар счастливца Пифагора.
С тех пор быки отчаянно ревут:
Навеки всполошило бычье племя
Событие, помянутое тут.
Им кажется: вот-вот настанет время,
И сызнова их в жертву принесут
Какой-нибудь великой теореме…
Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим И таким простым путём К результату мы придём.
Применение теоремы Пифагора
Успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов, которые позволяют решать задачи, выдвигаемые практикой. Теорема Пифагора применяется в строительстве, астрономии, мобильной связи, литературе и т.д.
Заключение
В научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).
Теорема Пифагора - одна из главных и, можно сказать, самая главная теорема геометрии. Теорема Пифагора триедина: это простота – красота – значимость. Мы познакомились с некоторыми доказательствами теоремы Пифагора.
Есть доказательства, которые рассчитаны на то, что по готовым рисункам, можно воспроизвести доказательство самостоятельно. А это воспитывает познавательный интерес и логическое мышление. До сих пор вызывают интерес древние практические задачи, говорящие об уровне развития прикладной математики в древние века.
Читайте также:

