Поверхностные интегралы первого рода кратко

Обновлено: 02.07.2024

Лекция 12.Площадь поверхности. Поверхностный интеграл первого рода, его свойства, геометрический и физический смысл. Вычисление поверхностного интеграла первого рода.

Если при определении длины кривой она задавалась как предел вписанной в данную кривую ломаной при стремлении к нулю длины наибольшего ее отрезка, то попытка распространить это определение на площадь криволинейной поверхности может привести к противоречию (пример Шварца: можно рассмотреть последовательность вписанных в цилиндр многогранников, у которых наибольшее расстояние между точками какой-либо грани стремится к нулю, а площадь стремится к бесконечности). Поэтому определим площадь поверхности иным способом. Рассмотрим незамкнутую поверхность S, ограниченную контуром L, и разобьем ее какими-либо кривыми на части S1, S2,…, Sn. Выберем в каждой части точку Mi и спроектируем эту часть на касательную плоскость к поверхности, проходящую через эту точку. Получим в проек-ции плоскую фигуру с площадью Ti. Назовем ρ наибольшее расстояние между двумя точками любой части поверхности S.

Определение 12.1. Назовем площадью S поверхности предел суммы площадей Ti при

. (12.1)

Поверхностный интеграл первого рода.

Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S1, S2,…, Sп (при этом площадь каждой части тоже обозначим Sп). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части Si точку Mi (xi, yi, zi) и составим интегральную сумму

. (12.2)

Определение 12.2. Если существует конечный предел при интегральной суммы (12.2), не зависящий от способа разбиения поверхности на части и выбора точек Mi, то он называется поверхностным интегралом первого рода от функ-ции f(M) = f(x, y, z) по поверхности S и обозначается

. (12.3)

Замечание. Поверхностный интеграл 1-го рода обладает обычными свойствами интегралов (линейность, суммирование интегралов от данной функции по отдельным частям рассматриваемой поверхности и т.д.).

Геометрический и физический смысл поверхностного интеграла 1-го рода.

Если подынтегральная функция f(M) ≡ 1, то из определения 12.2 следует, что равен площади рассматриваемой поверхности S.

Если же считать, что f(M) задает плотность в точке М поверхности S, то масса этой поверхности равна

. (12.4)

Вычисление поверхностного интеграла 1-го рода.

Ограничимся случаем, когда поверхность S задается явным образом, то есть уравне-нием вида z = φ(x, y). При этом из определения площади поверхности следует, что

Si = , где Δσi – площадь проекции Si на плоскость Оху, а γi – угол между осью Oz и нормалью к поверхности S в точке Mi. Известно, что

где (xi, yi, zi) – координаты точки Mi. Cледовательно,

Подставляя это выражение в формулу (12.2), получим, что

где суммирование справа проводится по области Ω плоскости Оху, являющейся проекцией на эту плоскость поверхности S (рис.1).

При этом в правой части получена интегральная сумма для функции двух переменных по плоской области, которая в пределе при дает двойной интеграл Таким образом, получена формула, позволяющая свести вычисление поверхностного интеграла 1-го рода к вычислению двойного интеграла:

(12.5)

Замечание. Уточним еще раз, что в левой части формулы (12.5) стоит поверхностный интеграл, а в правой – двойной.

Вычислим , где S – часть плоскости 3х + 4у – 5z = 36, расположенная в пер-вом октанте. Преобразуем это уравнение к виду , откуда ,

, . Проекцией плоскости S на плоскость Оху является тре-угольник с вершинами в точках (0, 0), (12, 0) и (0, 9). Тогда из формулы (12.5) полу-чим:

Разобьём поверхность на $n$ частей $\sigma _1 ,\sigma _2 ,\ldots \sigma _i ,\ldots \sigma _n $, на каждой из частей $\sigma _i $ выберем произвольную точку $M_i (x_i ,y_i ,z_i )$, найдём $f(M_i )=f(x_i ,y_i ,z_i )$ и площадь части $\sigma _i $ < которую будем обозначать тем же символом $\sigma _i )$ и составим интегральную сумму $\sum\limits_ < i=1 >^n < f(M_i )\cdot \sigma _i >$.

Если существует предел последовательности интегральных сумм при $\mathop < \max >\limits_ < i=1,2,\ldots n >diam\sigma _i \to 0$, не зависящий ни от способа разбиения поверхности $\sigma $ на части $\sigma _i (i=1,2,\ldots ,n)$, ни от выбора точек $M_i $, то функция $\mathbf < \textit < f >> (\mathbf < \textit < x >> $,$\mathbf < \textit < y >> $,$\mathbf < \textit < z >> )$ называется интегрируемой по поверхности $\sigma $, а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности и обозначается $\iint\limits_\sigma < f(M)\cdot d\sigma >$.

Теорема существования Если функция $\mathbf < \textit < f >> (\mathbf < \textit < x >> $,$\mathbf < \textit < y >> $,$\mathbf < \textit < z >> )$ непрерывна на поверхности $\sigma $, то она интегрируема по этой поверхности.

Свойства поверхностного интеграла первого рода

Аналогичны по формулировке и доказательству свойствам рассмотренных ранее интегралов первого рода.

Линейность. $\iint\limits_\sigma < (\lambda \,f+ >\mu \,g)d\sigma =\lambda \iint\limits_\sigma < fd\sigma >+\mu \iint\limits_\sigma < gd\sigma >$
Аддитивность $\iint\limits_ < \sigma _1 \cup \sigma _2 >< fd\sigma >=\iint\limits_ < \sigma _1 >< fd\sigma >\iint\limits_ < \sigma _2 >< fd\sigma >$
$\iint\limits_\sigma < d\sigma >=S_\sigma -$ площадь поверхности.
Если $f(x,\,y,\,z)\geqslant g(x,\,y,\,z)$, то $\iint\limits_\sigma < fd\sigma \geqslant \iint\limits_\sigma < gd\sigma >> $ < если $f\geqslant 0$, то $\iint\limits_\sigma < fd\sigma >\geqslant 0)$,
Теорема об оценке Если $m\leqslant f\left( < x,\,y,\,z >\right)\leqslant M$, то $mS_\sigma \leqslant \iint\limits_\sigma < fd\sigma >\leqslant MS_\sigma $,
Теорема о среднем Пусть функция $f(M)=f(x,\,y,\,z)$ непрерывна на кусочно-гладкой ограниченной поверхности $\sigma $. Тогда на поверхности найдется точка С, такая что $f(C)=\frac < 1 >< S_\sigma >\iint\limits_\sigma < f\left( < x,\,y,\,z >\right)d\sigma > $

Доказательство

Первые четыре свойства доказываются аналогично подобным свойствам в двойном, тройном интегралах, криволинейном интеграле первого рода < записью соотношений в интегральных суммах и предельным переходом >. Во втором свойстве используется возможность такого разбиения поверхности на две части, чтобы ни один элемент разбиения не содержал граничные точки этих частей в качестве своих внутренних точек.

Теорема об оценке следует из свойств 3, 4.

Теорема о среднем, как и ранее, использует теоремы Вейерштрасса и Больцано-Коши для функций, непрерывных на замкнутых ограниченных множествах.

Седьмое, персональное, свойство - независимость поверхностного интеграла первого рода от выбора стороны поверхности

Соленоидальное векторное поле

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Свойства тройного интеграла

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина

Теорема об алгоритме распознавания полноты

Вычисление поверхностного интеграла второго рода

Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе

Критерий полноты . Лемма о несамодвойственной функции

Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному

Вычисление криволинейного интеграла первого рода. Примеры

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Свойства криволинейного интеграла второго рода

Критерий полноты . Лемма о немонотонной функции

СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице

Пусть функция определена и непрерывна на некоторой поверхности в пространстве Разобьем поверхность произвольным образом на n частей с площадями (рис. 8.1). В каждой частичной области выберем произвольную точку и составим сумму

которую назовем интегральной суммой для функции в области (на поверхности) . Обозначим через наибольший из диаметров частичных областей :

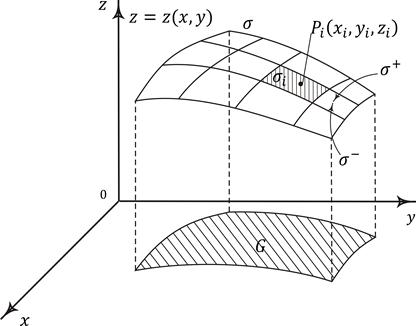
Рис. 8.1. Разбиение поверхности на частичные области в случае

поверхностного интеграла первого рода

Определение. Поверхностным интегралом первого рода от функции по поверхности называется предел интегральных сумм при , если этот предел существует и не зависит ни от способа разбиения поверхности на частичные области , ни от выбора в каждой из них точки :

или в другой записи:

Функция называется интегрируемой по поверхности , сама – поверхностью интегрирования.

Определение. Поверхность называется гладкой, если в каждой ее точке существует касательная плоскость и при переходе от точки к точке положение этой касательной плоскости меняется непрерывно.

Поверхность, состоящая из конечного числа гладких кусков, которые соединены непрерывно, называется кусочно-гладкой.

Теорема 8.1 (существования поверхностного интеграла первого рода) (без доказательства). Функция , непрерывная на кусочно-гладкой поверхности , интегрируема по этой поверхности.

Замечание. Если положить всюду на поверхности , то из определения поверхностного интеграла первого рода легко получить формулу для вычисления площади S поверхности с помощью поверхностного интеграла первого рода:

Основные свойства поверхностного интеграла первого рода аналогичны соответствующим свойствам криволинейного интеграла первого рода:

Свойство 1. Постоянный множитель можно выносить за знак интеграла:

Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:

Свойство 3. Если поверхность разбить на две поверхности и , то интеграл по всей поверхности будет равен сумме интегралов по поверхностям и :

Свойство 4 (Теорема о среднем). Если функция непрерывна вдоль гладкой поверхности , то на этой поверхности существует такая точка , что справедлива формула

где S – площадь поверхности .

Свойство 5. При изменении стороны поверхности интегрирования величина интеграла не изменяется:

где и – стороны поверхности интегрирования .

Вычисление поверхностного интеграла первого рода сводится к вычислению двойного интеграла следующим способом.

Если поверхность задана уравнением и область G – проекция поверхности на плоскость Oxy (рис. 8.1), то

Аналогично записываются формулы, выражающие интеграл по поверхности через двойные интегралы по проекциям на плоскости Oyz и Oxz.

Пример. Вычислить поверхностный интеграл первого рода

где – часть плоскости , лежащая в первом октанте (рис. 8.2).

Из уравнения поверхности имеем

Поверхность проектируется на плоскость Oxy в область G, ограниченную прямыми .

По формуле вычисления поверхностного интеграла первого рода имеем:

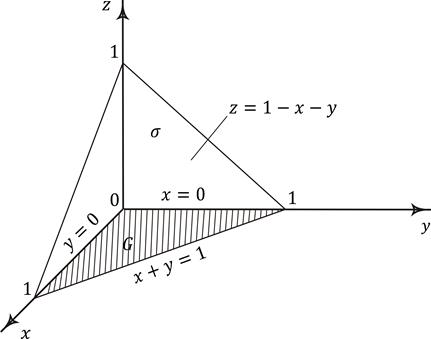
Рис. 8.2. Пример вычисления поверхностного интеграла первого рода

Рис. 8.1. Разбиение поверхности на частичные области в случае

поверхностного интеграла первого рода

или в другой записи:

Функция называется интегрируемой по поверхности , сама – поверхностью интегрирования.

Свойство 1. Постоянный множитель можно выносить за знак интеграла:

где S – площадь поверхности .

Свойство 5. При изменении стороны поверхности интегрирования величина интеграла не изменяется:

где и – стороны поверхности интегрирования .

Если поверхность задана уравнением и область G – проекция поверхности на плоскость Oxy (рис. 8.1), то

Пример. Вычислить поверхностный интеграл первого рода

где – часть плоскости , лежащая в первом октанте (рис. 8.2).

Из уравнения поверхности имеем

Поверхность проектируется на плоскость Oxy в область G, ограниченную прямыми .

Криволинейный интеграл 1 рода от функции ƒ(x,y) по кривой (L) :

где Δl_k(k = 1,n ) - длины дуг, на которые разбита кривая;

δ -наибольшая из длин дуг;

(ς_k, η_k) -произвольная точка на k-м участке.

Если р=р(х,у) - плотность неоднородной материальной кривой L,

масса плоской кривой,

длина плоской кривой L.

Если у = ƒ(x,y) - направляющая цилиндрической поверхности, образующая которой параллельна оси OZ, то

- площадь L поверхности, задаваемой функцией у = ƒ(x,y)

Поверхностный интеграл 1 рода от функции ƒ(x,y,z) по поверхности:

где Δσ_k(k = 1,n ) - площади участков, на которые разбита поверхность σ;

δ — наибольший из диаметров участков;

Если р = р(х, у, z) - плотность распределения массы материальной поверхности σ,

масса поверхности.

площадь поверхности σ

Замечание. Свойства криволинейного и поверхностного интегралов 1 рода аналогичны.

Аддитивность по функции

Аддитивность по области интегрирования

где путь интегрирования L= Цд>Ь₂

Теорема о среднем

Интеграл по модулю

Незваисимость интеграла от направления пути интегрирования

Криволинейные и поверхностные интегралы 2 рода (по координатам)

Определение и обозначение интеграла 2 рода

Геометрический и физический смысл

Криволинейный интеграл 2 рода от векторной функции

где Δx_k - проекция элементарной дуги Δl_k на ось ОХ;

- криволинейный интеграл по замкнутой кривой L

вектор силы, перемещающей точку по кривой L,

- работа переменной силы по перемещению точки вдоль кривой,

- площадь области D, где δD - граница области D

Поверхностный интеграл 2 рода от векторной функции

- единичный вектор нормали к Δσ_i;

- интеграл по замкнутой a поверхности a

- вектор скорости потока жидкости, протекающей через двустороннюю поверхность σ, одна из сторон которой выбрана для построения нормалей,

- поток a жидкости через выбранную сторону поверхности σ

Замечание. Свойства аддитивности и однородности криволинейного и поверхностного интегралов 2 рода аналогичны.

Читайте также:

Поверхностные интегралы первого рода кратко

Далее:

Криволинейные и поверхностные интегралы 2 рода (по координатам)