Поле заряженного шара кратко

Обновлено: 04.07.2024

Пользуясь тем, что гауссова поверхность (в законе Гаусса) произвольная, выберем её в виде концентрической сферы, с заряженным шаром. В силу симметрии, на всей гауссовой поверхности электрическое поле будет одинаково.

Выносим его из под знака интеграла в законе Гаусса:

То есть - вне шара такое же поле, как от точечного заряда.

Для нахождения поля вне шара не важно, как распределён заряд внутри шара - по поверхности, или по объёму; лишь бы симметрично.

Потенциал от заряженного шара вычислим через электрическое поле, при этом удобно ноль потенциала установить на бесконечности. Общая формула для потенциала всевозможных шаров (полых, сплошных):

Подставляя вместо E найденные значения, получим:

· любой шар, потенциал вне шара (такой же, как от точечного заряда):

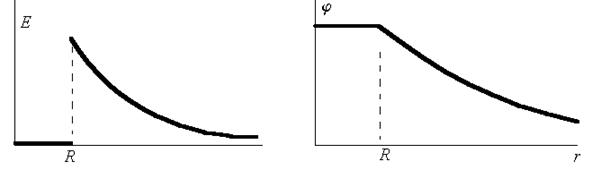
· внутри полого шара потенциал не меняется (R - радиус шара):

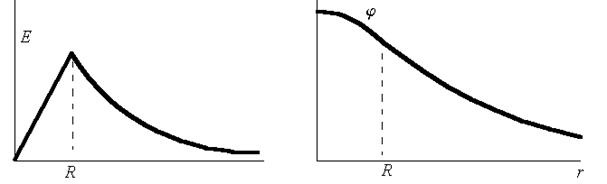
· внутри заряженного равномерно по объёму сплошного шара:

Графики полей и потенциалов имеют вид:

· Полый шар (заряд на поверхности):

· Сплошной шар, равномерно заряженный по объёму:

Выносим его из под знака интеграла в законе Гаусса:

То есть - вне шара такое же поле, как от точечного заряда.

Когда заряд распределен по какой-либо поверхности, то для расчета полей удобно ввести поверхностную плотность заряда с. Выделим на плоской поверхности маленький участок площадью ΔS. Пусть заряд этого участка равен Δq. Поверхностной плотностью заряда называют отношение заряда Δq к площади поверхности, по которой он распределен:

Эта плотность может непрерывно изменяться вдоль поверхности. Конечно, электрический заряд имеет дискретную (прерывную) структуру, так как сосредоточен в элементарных частицах. Но если на поверхности площадью ΔS содержится огромное число элементарных зарядов, то дискретную структуру заряда можно не принимать во внимание. Мы ведь пользуемся понятием плотности, считая, что масса непрерывно распределена в пространстве. А на самом деле все тела состоят из дискретных образований — атомов.

В случае равномерного распределения заряда q по поверхности площадью S поверхностная плотность заряда постоянна и равна:

Рассмотрим бесконечную равномерно заряженную плоскость. Поверхностная плотность заряда σ известна. Из соображений симметрии очевидно, что линии напряженности представляют собой прямые, перпендикулярные плоскости. Поле бесконечной плоскости — однородное поле. Во всех точках пространства, независимо от расстояния до плоскости, напряженность поля одна и та же.

Для применения теоремы Гаусса нужно выбрать замкнутую поверхность таким образом, чтобы можно было легко вычислить поток напряженности электрического поля через эту поверхность. В данном случае удобнее всего выбрать цилиндр, образующие которого параллельны линиям напряженности электрического поля, а основания параллельны плоскости (рис. 1.43).

Тогда поток через боковую поверхность цилиндра будет равен нулю. Поэтому полный поток равен потоку через основания цилиндра А и В:

где Е_n — проекция вектора напряженности на нормаль к основанию цилиндра. Полный заряд внутри цилиндра равен σS. Согласно теореме Гаусса

Отсюда модуль напряженности равен:

В СИ эта формула принимает вид:

а в абсолютной системе

Поле равномерно заряженной сферы

Поток напряженности электрического поля через любую замкнутую поверхность внутри сферы равен нулю, так как равен нулю заряд. Это может быть лишь в том случае, когда напряженность поля внутри сферы равна нулю.

Найдем напряженность поля вне сферы. Из соображений симметрии ясно, что линии напряженности начинаются на поверхности сферы (в случае положительного заряда), направлены по радиусам сферы и перпендикулярны ее поверхности (рис. 1.44). Поэтому модуль напряженности поля одинаков во всех точках, лежащих на одинаковых расстояниях от центра сферы.

Проведем сферическую поверхность радиусом r > R, где R — радиус заряженной сферы. Поток напряженности через эту поверхность равен:

Если заряд сферы q, то по теореме Гаусса

Следовательно, модуль напряженности поля при r > R равен:

Таким образом, поле заряженной сферы совпадает вне сферы с полем точечного заряда, расположенного в центре сферы. График зависимости Е(r) изображен на рисунке 1.45.

Поле равномерно заряженного шара

Для характеристики распределения заряда по объему используется понятие объемной плотности заряда. Объемной плотностью заряда называется отношение заряда Δq к объему ΔV, в котором он распределен:

Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд q равномерно распределен по объему V, то объемная плотность заряда постоянна и равна:

Будем считать, что шар радиусом R равномерно заряжен; плотность заряда ρ известна. Полный заряд шара

Напряженность электрического поля вне шара можно найти с помощью теоремы Гаусса точно так же, как и напряженность равномерно заряженной сферы [см. формулу (1.12.9)]:

(при условии, что r > R). Поле аналогично полю точечного заряда q, расположенного в центре шара.

Для нахождения поля внутри шара нужно применить теорему Гаусса к потоку напряженности через сферическую поверхность радиусом к

Напряженность электрического поля линейно растет с увеличением расстояния вплоть до u = R. При r > R она определяется формулой (1.12.12). График модуля напряженности поля в зависимости от расстояния до центра представлен на рисунке 1.47.

Вопрос для самопроверки

Заряженный лист фольги имеет такие же размеры, как страница из тетради. Можно ли определить напряженность электрического поля, созданного листом, на расстоянии 0,5 см от него, используя формулу (1.12.4)?

* Мы предполагаем, что диэлектрическая проницаемость среды одинакова внутри и вне шара.

Посмотрев данный видеоурок, учащиеся познакомятся с графической интерпретацией электрических полей. Научатся рассчитывать напряжённость поля, создаваемого точечным электрическим зарядом и заряженным проводящим шаром. Также в этом уроке мы сформулируем принцип суперпозиции электрических полей.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Поле точечного заряда и заряженного шара. Принцип суперпозиции полей"

Вам известно, что электрическое поле не действует на наши органы чувств, его невозможно увидеть. Но мы можем получить некоторое представление о распределении поля в пространстве. Для этого давайте изобразим векторы напряжённости поля, создаваемого неподвижным зарядом, в нескольких точках пространства.

Впервые этот способ изображения электрических полей в виде воображаемых линий, называемых линиями напряжённости (или силовыми линиями), был предложен в 1845 году Майклом Фарадеем.

Под линиями напряжённости мы с вами будем понимать воображаемые направленные линии, касательные к которым в каждой точке поля совпадают по направлению с напряжённостью электрического поля в той же точке.

Интересно, но сам Фарадей считал, что силовые линии существуют в действительности и похожи на растянутые упругие нити. Сейчас же мы точно знаем, что они не более реальны, чем земные меридианы и параллели, изображаемые на глобусах.

При построении линий напряжённости необходимо придерживаться следующих правил. Во-первых, касательная к линии напряжённости в каждой точке должна совпадать с направлением вектора напряжённости.

Во-вторых, следует помнить, что линии напряжённости электростатического поля — это незамкнутые линии: они начинаются на поверхности положительных зарядов и оканчиваются на поверхности отрицательных зарядов (или в бесконечности). В-третьих, линии напряжённости не должны пересекаться, так как в каждой точке поля вектор напряжённости имеет лишь одно направление.

И, наконец, чтобы линии напряжённости отображали не только направление, но и модуль напряжённости поля, на рисунках их условились проводить с определённой густотой: их рисуют гуще там, где модуль напряжённости поля больше, и реже — где он меньше.

На рисунке вы видите пример линий напряжённости двух пластин, заряды которых равны по модулю и противоположны по знаку.

Обратите внимание, что в пространстве между пластинами линии напряжённости практически параллельны друг другу (за исключением пространства вблизи краёв пластин и вне области их перекрытия) и находятся на равных расстояниях друг от друга: здесь электростатическое поле одинаково во всех точках. Так вот, если напряжённость поля одинакова во всех его точках, то такое поле называется однородным.

Теперь давайте посмотрим, как рассчитывается напряжённость электростатического поля, созданного точечным зарядом, модуль которого равен |Q|. Для этого поместим в некоторую точку поля положительный пробный заряд q₀.

Согласно закону Кулона, на пробный заряд со стороны поля будет действовать сила, модуль которой прямо пропорционален произведению модулей обоих зарядов и обратно пропорционален квадрату расстояния между зарядом, создающим поле, и точкой, в которую помещён пробный заряд:

Далее вспомним, что по определению, модуль напряжённости в данной точке поля равен отношению модуля силы, с которой поле действует на пробный заряд, находящийся в выбранной точке, к величине этого заряда:

Подставим выражение для модуля кулоновской силы в формулу для модуля напряжённости поля:

По полученной формуле мы с вами можем рассчитать напряжённость в любой точке поля, созданного неподвижным точечным зарядом.

Если же точечный заряд, создающий поле, находится в какой-либо проводящей среде, то в знаменатель формулы следует добавить множитель значения её диэлектрической проницаемости ε:

По этой же формуле можно рассчитывать напряжённость поля, образованного равномерно заряженным шаром в точках, которые находятся на его поверхности и вне его. Внутри же заряженного шара (или проводящей сферы), как мы увидим дальше, напряжённость поля равна нулю:

А теперь давайте подумаем, как найти напряжённость в некоторой точке поля, если оно создано не одним, а несколькими зарядами.

Очевидно, что если поместить в исследуемую точку такого поля пробный заряд, то на него будут действовать кулоновские силы со стороны каждого из зарядов в отдельности, создающих поле. Из механики мы знаем, что если на тело действует несколько сил, то результирующая сила равна их геометрической сумме. То же самое справедливо и для электрических сил:

Разделим записанное равенство на величину пробного заряда:

И учтём, что отношение силы, действующей на пробный заряд со стороны электрического поля, к величине этого заряда, есть напряжённость:

Последнее равенство выражает принцип суперпозиции полей: напряжённость в любой точке электрического поля системы зарядов равна геометрической сумме напряжённостей полей, создаваемых в этой точке каждым из зарядов в отдельности:

При этом напряжённость поля, создаваемого отдельным зарядом, определяется так, как будто других зарядов вокруг не существует.

А теперь для закрепления материала решим с вами несколько задач. Задача 1. Заряженный шарик радиусом 5 сантиметров находится в среде, диэлектрическая проницаемость которой равна 2. Найдите напряжённость поля в точке, удалённой от поверхности шарика на 3 сантиметра, если заряд шарика равен 3 пКл.

Задача 2. Электрическое поле создаётся двумя точечными зарядами 30 нКл и – 10 нКл, находящимися в вакууме на расстоянии 5 см друг от друга. Определите напряжённость поля в точке, находящейся на расстоянии 3 см от первого заряда и 4 см от второго.

Одной из самых трудных задач, которую пришлось нам решать, когда мы изучали теорию гравитационного притяжения, было доказать, что сила, создаваемая твердым шаром на его поверхности, такая же, как если бы все вещество шара было сконцентрировано в его центре. Много лет Ньютон не решался обнародовать свою теорию тяготения, так как не был уверен в правильности этой теоремы. Мы доказали ее в вып. 1, гл. 13, взяв интеграл для потенциала и вычислив силу тяготения по градиенту. Теперь эту теорему мы можем доказать очень просто. Но на этот раз мы докажем не совсем ее, а сходную теорему для однородно заряженного электричеством шара. (Поскольку законы электростатики и тяготения совпадают, то то же доказательство может быть проведено и для поля тяготения.)

Фигура 4.11. Применение закона Гаусса для определения поля однородно заряженного шара.

1 — распределение заряда ; 2 — гауссова поверхность .

Закон Гаусса утверждает, что этот поток равен суммарному заряду сферы (деленному на ):

а это как раз та формула, которая получилась бы для точечного заряда . Мы решили проблему Ньютона проще, без интеграла. Конечно, это кажущаяся простота; вам пришлось затратить какое-то время на то, чтобы разобраться в законе Гаусса, и вы можете думать, что на самом деле время нисколько не сэкономлено. Но когда вам придется часто применять эту теорему, то она практически окупится. Все дело в привычке.

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Читайте также: