Параллельный перенос это кратко

Обновлено: 28.06.2024

Параллельным переносом называют изменение плоскости со смещением точек в одинаковом направлении на определенное расстояние.

Параллельный перенос строго определяют через декартовы координаты или через вектор. Предположим, что на плоскости имеются декартовы координаты х и у. Сформулируем тогда определение параллельного переноса.

Параллельный перенос представляет собой преобразование фигуры F с переходом какой-то точки с координатами (х;у) в точку с координатами (х+а; у+b), где а и b обозначают некие числа, одинаковые для каждой из точек (х;у), принадлежащих фигуре F.

Далее рассмотрим определение параллельного переноса через вектор.

Параллельный перенос на заданный вектор a ¯ является отображением плоскости на саму себя, при котором предусмотрено отображение каждой точки А в такую точку А 1 , что вектор А А 1 соответствует вектору a ¯ :

В рамках некой плоскости выражение параллельного переноса с аналитической точки зрения в прямоугольной системе координат ( x , y ) предусматривает следующее:

( x , y ) ↦ ( x + a , y + b ) ,

Здесь вектор определяется значением:

С помощью параллельного переноса происходит перемещение любой из точек фигуры или пространства на одинаковое расстояние в одинаковом направлении. В качестве доказательства изобразим этот процесс наглядно на примере рисунке:

Свойства, которыми обладает параллельный перенос в пространстве

В процессе параллельного переноса можно наблюдать смещение некой фигуры, в том числе, квадрата, относительно параллельных прямых на одинаковое расстояние. При этом возможен переход перпендикулярных прямых в прямые, которые также являются перпендикулярными.

Вместе с тем, параллельные прямые трансформируются в прямые, которые также являются параллельными. Параллельный перенос некой фигуры не сопровождается изменением расстояния, на которое удалены ее точки, и углов между прямыми. Данные характеристики сохраняются без корректировок.

Перечислим характерные свойства, которыми обладает параллельный перенос:

Параллельный перенос можно определить, как вид движения, то есть в процессе переноса расстояние сохраняется без изменений.
В процессе параллельного переноса происходит смещение точек по параллелям или прямым, которые совпадают, на одинаковое расстояние.
Если реализован параллельный перенос, то каждая из прямых перейдет в результате в прямую, которая является ей параллельной, либо в саму себя.
При любых точках А и А 1 допустим лишь один параллельный перенос, предполагающий переход точки А в точку А 1 .

С параллельным переносом можно столкнуться при изучении многих предметов, в том числе, физики и геометрии. Например, в алгебре с помощью параллельного переноса упрощается построение графиков для решения легких и сложных задач в классе.

Формула параллельного переноса

Предположим, что на плоскости, где расположены оси О х и О у , построена фигура. Обозначим ее S . В процессе параллельного переноса можно наблюдать переход каждой из точек рассматриваемой фигуры в точку А' на одинаковое расстояние.

Из вышесказанного можно сделать вывод о том, что трансформация фигуры S в фигуру S ' при смещении каждой из точек фигуры, в том числе, окружности, с координатами х и у в точку с координатами x + a и y + b , где a и b постоянные числа, определяется, как параллельный перенос. Таким образом, параллельный перенос является движением, при котором каждая из точек фигуры перемещается на одинаковое расстояние.

Получить координаты новой фигуры, образованной в результате параллельного переноса, можно с помощью следующих формул:

A B 2 = ( x B - x A ) 2 + ( y B - y A ) 2

A ' B ' 2 = ( x B ' - x A ' ) 2 + ( y B ' - y A ' ) 2

Переход точки A ( x ; y ) в точку A 1 ( x 1 ; y 1 ) при параллельном переносе A ( x ; y ) → A 1 ( x 1 ; y 1 ) можно описать с помощью уравнения:

x 1 = x + a y 1 = y + b

В некоторых литературных источниках можно встреть такую формулировку теоремы, как: точка А 1 представляет собой образ точки А , что возможно при реализации параллельного переноса на вектор ( a ; b ). В таком случае точка A является прообразом.

Виды параллельного переноса

Запишем виды движения в пределах некоторой плоскости:

параллельный перенос любой фигуры, в том числе, трапеции;
осевая симметрия;
поворот вокруг точки;
центральная симметрия.

При параллельном переносе поступательное движение точек представляет собой перемещение в одинаковом направлении на одинаковое расстояние. Таким образом, происходит отражение фигуры на плоскости. При перемещении точек на одинаковый вектор, данный вектор называют вектором переноса.

Так как параллельный перенос характеризуется свойством, при котором в процессе движения не меняется направление, справедливым является и обратное утверждение. В результате, движение при стабильном направлении можно считать параллельным переносом.

Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.

Чтобы совершить параллельный перенос, нужно знать направление и расстояние, что означает задать вектор.

Чтобы при параллельном переносе построить изображение многоугольника, достаточно построить изображения вершин этого многоугольника.

Если одна фигура получена из другой фигуры поворотом всех её точек относительно центра $O$ на один и тот же угол в одном и том же направлении, то такое преобразование фигуры называется поворотом .

Против часовой стрелки — положительный угол поворота, наоборот — отрицательный угол поворота (так же как углы поворота в единичной окружности).

Если угол поворота равен $180$ или $-180$ градусам, то фигура отображается как центрально симметричная данной, и этот поворот называется случаем центральной симметрии.

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

$A(x;y) \to <A_1> (;),$

то параллельный перенос задаётся формулами:

$\left\< \begin = x + a\\ = y + b \end \right.$

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

$\overline <A<A_1> > = \overline a$

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

В данном видеофрагменте мы вспомним, какое отображение плоскости на себя мы называли параллельным переносом. Введем понятие параллельного переноса в пространстве. Проверим, будет ли параллельный перенос движением пространства.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Параллельный перенос"

Сегодня на уроке мы вспомним, какое отображение плоскости на себя мы называли параллельным переносом, введём понятие параллельного переноса в пространстве. Проверим, будет ли параллельный перенос движением пространства.

Вернёмся в планиметрию и вспомним, что параллельным переносом мы называли преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние. Мы говорили, что для того, чтобы задать перенос достаточно задать вектор.

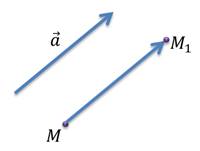
Другими словами, параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка отображается в такую точку , что вектор равен вектору .

То, что параллельный перенос является примером движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.

Пусть при параллельном переносе на вектор точки и отображаются в точки и . Так как векторы и , то значит, эти векторы равны между собой . То есть они параллельны и их длины равны, поэтому четырёхугольник – параллелограмм. Следовательно, , то есть расстояние между точками и равно расстоянию между точками и .

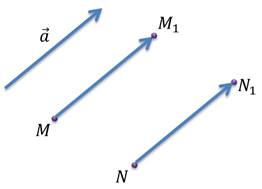
Случай, когда точки и лежат на прямой параллельной вектору , вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между точками и будет равно расстоянию между точками и .

Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение. Это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

В планиметрии мы говорили, что параллельный перенос обладает некоторыми свойствами.

Свойства параллельного переноса:

· При параллельном переносе отрезок переходит в равный ему отрезок.

· Угол переходит в равный ему угол.

· Окружность переходит в равную ей окружность.

· Любой многоугольник переходит в равный ему многоугольник.

· Параллельные прямые переходят в параллельные прямые.

· Перпендикулярные прямые переходят в перпендикулярные прямые.

Теперь давайте определим, что мы будем понимать под параллельным переносом в пространстве.

Определение:

Параллельным переносом на вектор называется такое отображение пространства на себя, при котором любая точка переходит в такую точку что .

Проверим, будет ли параллельный перенос в пространстве примером движения пространства.

При параллельном переносе точки пространства и переходят в такие точки и , что вектора и .

Сложим по правилу треугольника векторы

Поскольку левые части равенств равны, значит, равны и правые части равенств.

Значит, можно записать, что .

Заменим вектора и на вектор . Получим, что . Отсюда получаем, что вектор . Поскольку векторы равны, значит, равны и их длины, то есть . То есть расстояние между точками при параллельном переносе в пространстве сохраняется, значит, параллельный перенос в пространстве также является движением, но уже не плоскости, а пространства.

Сформулируем свойства параллельного переноса.

Свойства параллельного переноса:

· Параллельный перенос является примером движения пространства.

· При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и то же расстояние.

· При параллельном переносе прямая переходит в параллельную прямую (или сама в себя).

· Каковы бы не были две точки и , существует, и притом единственный, параллельный перенос, при котором точка переходит в точку .

· При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

Движение в пространстве обладает теми же свойствами, что и движение плоскости.

Свойства движения пространства:

· Движение сохраняет расстояние между точками.

· При любом движении пространства отрезок отображается на отрезок, прямая – в прямую, плоскость – в плоскость.

Решим несколько задач.

Задача: начертить отрезок и вектор . Построить отрезок , который получится из отрезка параллельным переносом на вектор .

Решение: для того, чтобы построить отрезок , отобразим точку в точку , точку в точку с помощью параллельного переноса. Тогда соединив точки , мы получим отрезок .

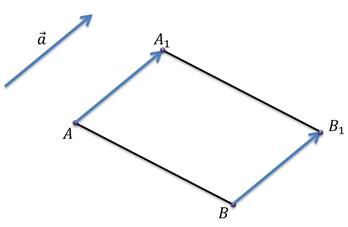
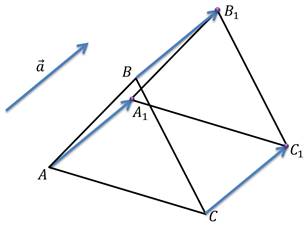
Задача: начертить треугольник и вектор . Построить треугольник , который получится из треугольникa параллельным переносом на вектор .

Решение: отобразим с помощью параллельного переноса точки , , в точки , ,. Соединив полученные точки, мы получим искомый треугольник .

Задача: начертить пятиугольник и вектор . Построить пятиугольник , который получится из пятиугольника параллельным переносом на вектор .

Решение: решать эту задачу будем аналогично тому, как мы решали предыдущую задачу. Отобразим каждую вершину пятиугольника с помощью параллельного переноса на вектор . Соединим получившиеся точки и получим искомый пятиугольник .

Сегодня на уроке мы вспомнили, что мы понимали под параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве. Сформулировали основные свойства параллельного переноса, движения пространства.

Читайте также: