Объемы наклонной призмы пирамиды и конуса кратко

Прямоугольные треугольники , тоже подобны (они имеют общий острый угол с вершиной О).

Применим теперь основную формулу для вычисления объемов тел при a = 0, b = h получаем

2. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S . Такую пирамиду можно разбить на треугольные пирамиды с общей высотой h. Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель , получим в скобках сумму оснований треугольных пирамид, т.е. площадь S оснований исходной пирамиды.

Таким образом, объем исходной пирамиды равен . Теорема доказана.

II. решить задачи по готовым чертежам .

Задача 1. (рис. 3)

Дано: АВСD – правильная пирамида, АВ = 3; AD= . Найти: а) Sосн ; б) АО; в) DO г) V .

Задача 2. (рис. 4)

Дано: АВСDF – правильная пирамида, .

Задача 3. (рис. 5)

Дано : АВСDEKF – правильная пирамида,

Найти: а) S _осн ; б) V.

Задача 4. (рис. 6)

Найти: V.

Проверка задач выполняется с помощью мультимедийного проектора с подробным анализом поэтапного решения.

Задача 1. (рис. 3)

а) (используется формула для вычисления площади правильного треугольника)
АВ = = 3, имеем

б) (формула радиуса описанной окружности через сторону правильного треугольника) .

Задача 2. (рис. 4)

1) Рассмотрим следовательно,
– равнобедренный, ОС = FО = 2.

Задача 3. (рис. 5)

Задача 4. (рис. 6)

Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис. 1).

Подставим это выражение для х в первую формулу,

Pабота в форме теста, с проверкой через мультимедийный проектор.

1.В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение - прямоугольный треугольник с катетами: 4 см и 3 см. найдите объем призмы.

а) 10 см 3 , б) 42 см 3 , в) 60 см 3 , г) 30 см 3 .

2. В правильной шестиугольной пирамиде сторона ее основания 2 см. Объем пирамиды равен 6 см 3 . Чему равна высота?

3. Объем пирамиды равен 56 см 3 , площадь основания 14 см 2 . Чему равна высота?

а) 14 см, б) 12 см, в) 16 см.

4. В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды?

5. В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. найдите объем пирамиды.

а) 50 см 3 , б) 48 см 3 , в) 16 см 3 .

6. Объем правильной четырехугольной пирамиды равен 27 см 3 , высота 9 см. найти сторону основания.

а)12 см, б) 9 см, в) 3 см.

7. Объем усеченной пирамиды равен 210 см 3 , площадь нижнего основания 36 см 2 , верхнего 9 см 2 . Найдите высоту пирамиды.

а) 1см, б) 15 см, в) 10см.

8. Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S?

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурс:

Теоретический материал для самостоятельного изучения

Призма называется наклонной, если ее боковые ребра не перпендикулярны основаниям.

Объем наклонной призмы — это произведение площади ее основания на высоту

Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.

Многогранник, гранями которого являются n- угольники и , расположенные в параллельных плоскостях и n четырехугольников , и так далее называется усечённой пирамидой.

Примеры и разбор решения заданий тренировочного модуля

№1. Найти объем наклонной треугольной призмы высотой 6, в основании которой - прямоугольный треугольник с катетами 3 и 7.

Решение: Объем призмы вычисляется по формуле , т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле , где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ: .

№2. Найти объём наклонной призмы, основанием которой является параллелограмм АВСD. Сторона АВ=3см, сторона AD=5см, . Высота призмы равна 8см.

Решение: воспользуемся только что доказанной формулой.

Для вычисления площади параллелограмма, лежащего в основании, воспользуемся формулой: .

Подставим полученное значение в формулу для вычисления объёма, получим, что объём призмы равен .

Ответ 60 см 3

№3 В правильной усечённой четырёхугольной пирамиде стороны основания равны 6см и 4см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15см 2 . Найти объём усеченной пирамиды.

Решение: воспользуемся формулой для вычисления объёма усечённой пирамиды.

Площадь оснований этой пирамиды найти нетрудно, эти площади равны и .

Рассмотрим сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Этим сечением будет трапеция, причем высота этой трапеции будет высотой усечённой пирамиды, потому что высотой усечённой пирамиды называется перпендикуляр, опущенный на нижнее основание.

Высоту мы найдём пользуясь формулой для вычисления площади трапеции.

Основания трапеции – диагонали квадратов, то есть основания трапеции соответственно равны и . Получим, что высота трапеции равна .

Подставив найденные значения в формулу для вычисления объёма усечённой пирамиды, мы получим, что объём усечённой пирамиды равен .

Ответ 38см 3

- сформировать навык по нахождению объема наклонной призмы.

I. Организационный момент

Проверка домашнего задания. Вывод формулы у доски.

II. Теорема об объеме наклонной призмы

Объем наклонной призмы равен произведению площади основания на высоту.

Рис. 1 на слайде (или ватм. лист).

1) Рассмотрим треугольную призму с объемом V и площадью основания S, высотой h.

Точка О принадлежит одному из оснований призмы, направим ось ох перпендикулярно основаниям. Рассмотрим сечение призмы плоскостью, перпендикулярной к оси ох и, значит, параллельно плоскости основания.

х - абсцисса точки пересечения этой плоскости с осью ох, площадь полученного сечения - S(x).

ΔАВС (основание призмы) = ΔА1В1С1 (сечение призмы), так как AА1В1В - параллелограмм

Аналогично: значит, равенство треугольников вытекает по 3 признаку (3 стороны);

По основной формуле:

2) Докажем для любой призмы с высотой h и площадью основания S.

Разбиваем призму на 3 призмы с общей высотой h. Выразим объем каждой призмы и сложим их. Вынося h за скобки, получаем сумму площадей оснований 3-угольных призм, т.е. площадь основания исходной призмы. Имеем: V = S · h.

III. Решение задач: № 682,680, 676.

Дома: п. 68, № 681, 683.

Решение задач у доски.

Найти объем наклонной призмы, у которой основанием является треугольник со сторонами 10 см, 10 см, 12 см, а боковое ребро равное 8 см, составляет с плоскостью основания угол 60°.

Дано: АВСА1В1С1 - наклонная призма, АВ = 10 см, ВС = 10 см, АС = 12 см, ВВ1 = 8 см, ∠B1BK = 60° (рис. 2).

1) (ф-ла Герона).

2) ΔBB1H - прямоугольный, так как В1Н - высота. В1Н = ВВ1 · sin60°;

3)

(Ответ: Vnp. = 192√3 см3.)

Основанием наклонной призмы является прямоугольник со сторонами а и b. Боковое ребро длины с составляет со смежными сторонами основания углы, равные φ. Найти объем призмы.

Дано: АВСDА1В1С1D1 - призма, ABCD - прямоугольник, АВ = а, AD = b, АА1 = с. ∠A1AD = ∠A1AB = φ (рис. 3).

1) ∠A1AD = ∠A1AB, значит, точка А1 проецируется на биссектрису ∠А. А1O ⊥ (ABC), АО - биссектриса ∠A.

3) ΔAA1M - прямоугольный, АМ = С · соsφ.

4) ΔАОМ - прямоугольный,

(Ответ: )

Объем наклонной призмы равен произведению бокового ребра на площадь сечения призмы, плоскостью, перпендикулярной к боковым ребрам и их пересекающей.

Или перпендикулярного ему сечения (рис. 4).

1) (МЕК) - плоскость перпендикулярного сечения призмы, (ABC) - плоскость основания. (МЕК) ∩ (ABC) по прямой PQ. АА1 ⊥ (МЕК), ⇒ АА1 ⊥ PQ.

2) Проведем высоту А1О - призмы, А1О ⊥ PQ.

3) (по признаку перпендикулярности прямой и плоскости).

4) (АА1О) || PQ в точке Н, ∠AHM - линейный угол двугранного угла ∠QPM. ∠AHM = φ, тогда ∠MAH = 90° - φ.

5) ΔМЕК - ортогональная проекция ΔАВС на плоскость перпендикулярного сечения.

6) (APQ) ⊥ (АМН), так как (APQ) проходит через PQ, перпендикулярно (АМН).

7) Из ΔАА1O:

8)

Что и требовалось доказать.

Произвольная призма состоит из треугольных призм, следовательно,

IV. Групповая работа по готовым чертежам

Оценивается работа всей группы, задаются теоретические вопросы в качестве проверки знания теоретического материала и дополнительного задания.

1. Дано: ВВ1С1С - ромб, B1С ⊥ (ABC), В1С = 3, ΔАВС - равносторонний, ВВ1 = 5 (рис. 5).

1) (по условию).

2)

3) ∠B1CK = 90° (по определению угла между прямой и плоскостью); В1С = 3. (Ответ: )

2. Дано: АВ = АС = 3 см; ВС = 2 см; АА1 = 4 см; ∠А1АН = 45°. Vnp. = Vкуба. (рис. 6).

Найти: а - ребро куба.

1) по формуле Герона;

2) AK ⊥ BС; M ∈ АК; ΔАА1Н - прямоугольный,

3. Дано: ABCDA1B1C1D1 - призма; ABCD - прямоугольник; АВ = 6 см; AD = 8 см, AA1B1B - квадрат; ∠KHF = 60° (рис. 7).

1.

2. КО - высота призмы; ΔКОН - прямоугольный,

3.

№ слайда 1

Объемы наклонной призмы, пирамиды, конуса Геометрия 11 класс Р.О.Калошина ГОУ лицей №533 Санкт-Петербург

№ слайда 2

План урока Вычисление объемов тел с помощью определенного интеграла Объем наклонной призмы Объем пирамиды Объем усеченной пирамиды Объем конуса Объем усеченного конуса Вопросы для закрепления

№ слайда 3

Вычисление объемов тел Приближенное значение объема тела равно сумме объемов прямых призм, основания которых равны площадям сечений тела, а высоты равны ∆xi = xi – xi – 1 Отрезок [a; b] разбит на n частей

№ слайда 4

Вычисление объемов тел с помощью определенного интеграла Основная формула для вычисления объемов тел: Где S(x) – непрерывная функция на отрезке [a; b].

№ слайда 5

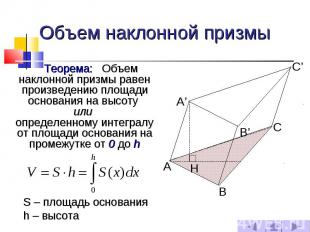
Объем наклонной призмы Теорема: Объем наклонной призмы равен произведению площади основания на высоту или определенному интегралу от площади основания на промежутке от 0 до h S – площадь основания h – высота

№ слайда 6

Объем наклонной призмы Объем произвольной призмы равен сумме объемов треугольных призм, которые получены путем разбиения основания на треугольники или произведению площади основания на высоту

№ слайда 7

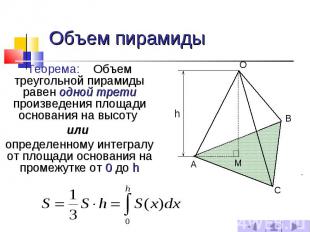
Объем пирамиды Теорема: Объем треугольной пирамиды равен одной трети произведения площади основания на высоту или определенному интегралу от площади основания на промежутке от 0 до h

№ слайда 8

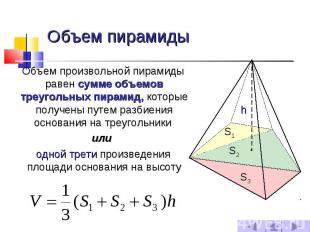
Объем пирамиды Объем произвольной пирамиды равен сумме объемов треугольных пирамид, которые получены путем разбиения основания на треугольники или одной трети произведения площади основания на высоту

№ слайда 9

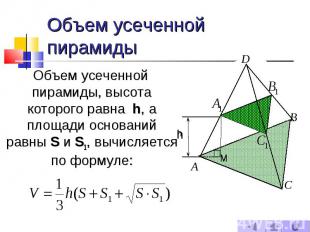
Объем усеченной пирамиды Объем усеченной пирамиды, высота которого равна h, а площади оснований равны S и S1, вычисляется по формуле:

№ слайда 10

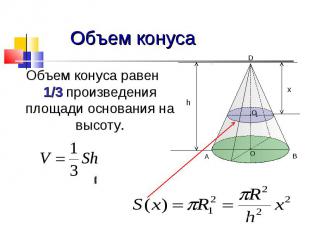
Объем конуса Объем конуса равен 1/3 произведения площади основания на высоту.

№ слайда 11

Объем конуса Объем конуса равен По основной формуле объема тела:

№ слайда 12

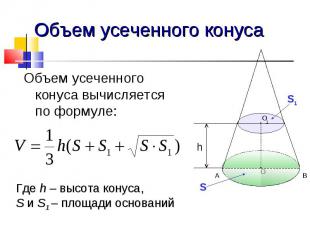
Объем усеченного конуса Объем усеченного конуса вычисляется по формуле: Где h – высота конуса, S и S1 – площади оснований

№ слайда 13

Вопросы для закрепления Чему равно приближенное значение объема тела? Чему равен объем наклонной призмы? Чему равен объем произвольной пирамиды? Чему равен объем усеченной пирамиды? Чему равен объем конуса? Чему равен объем усеченного конуса?

Читайте также:

  
• The long dark сюжет кратко
  
• Открытие м неводчиковым алеутских островов кратко
  
• Конрад хилтон история успеха кратко
  
• Начало династии сефевидов кратко
  
• Создание советских вооруженных сил их структура и предназначение обж кратко