Нейронную сеть хопфилда кратко

Обновлено: 30.06.2024

Нейронная сеть Хопфилда представляет собой однослойную нейронную сеть, которая реализует ассоциативную память образов. С помощью сети Хопфилда можно восстанавливать зашумленные образы.

В отличии от классических нейронных сетей обучение сети Хопфилда осуществляется достаточно просто. При этом процедура воспоминания образов представляет собой итеративную процедуру.

Посмотрим, как выглядят сети Хопфилда на нашей видео-лекции:

Опишем алгоритм работы сети Хопфилда. На первом этапе нужно обучить сеть, предъявляя ей различные эталонные образы. Пусть каждый образ представляет собой N-мерный вектор
x=[x₁,x₂. x_N],
где x_i равняется -1 или 1.

Результатом обучения сети Хопфилда будет матрица, которая отражает веса взаимодействия нейронов. В сети Хопфилда все нейроны взаимодействуют со всеми. В начале обучения все веса принимают нулевые значения. Далее для всех i и j, которые меняются от 1 до N, мы осуществляем следующую процедуру:

Для всех образов выполняем корректировку весов:
w_ij=w_ij + x_ix_j,
далее положим
w_ii=0
и нормируем
w_ij:=w_ij/N.
Все, наша сеть обучена!

Процедура распознавания образов осуществляется следующим алгоритмом. Пусть мы ищем образ
Y=[y₁,y₂. y_N],

Цикл по j от 1 до N:
Положим d = 0
Вложенный цикл по i от 1 до N:
d = d + w_ijy_i
Конец вложенного цикла
Если d > 0, то положить z_j = 1, иначе z_j = -1.
Конец внешнего цикла
Мы получили вектор:
Z=[z₁,z₂. z_N],
Если вектор Z содержится во множестве исходных образов, то считаем, что алгоритм нашел образ Z, который соответствует исходному образу Y.
Положим Y = Z
Переход к шагу 1.

Если наш алгоритм не может найти образ, то значит, что сеть Хопфилда не смогла "вспомнить" такой образ.

Посмотрим на видео как работает сеть Хопфилда:

Исходный текст этой программы доступен по адресу AI-HopfieldNET.

Статья посвящена введению в нейронные сети и примеру их реализации. В первой части дано небольшое теоретическое введение в нейронные сети на примере нейронной сети Хопфилда. Показано, как осуществляется обучение сети и как описывается ее динамика. Во второй части показано, как можно реализовать алгоритмы, описанные в первой части при помощи языка С++. Разработанная программа наглядно показывает способность нейронной сети очищать от шума ключевой образ. В конце статьи есть ссылка на исходный код проекта.

Введение

Для начала, необходимо определить, что такое нейрон. В биологии нейрон — специализированная клетка, из которой состоит нервная система. Биологический нейрон имеет строение, показанное на рис.1.

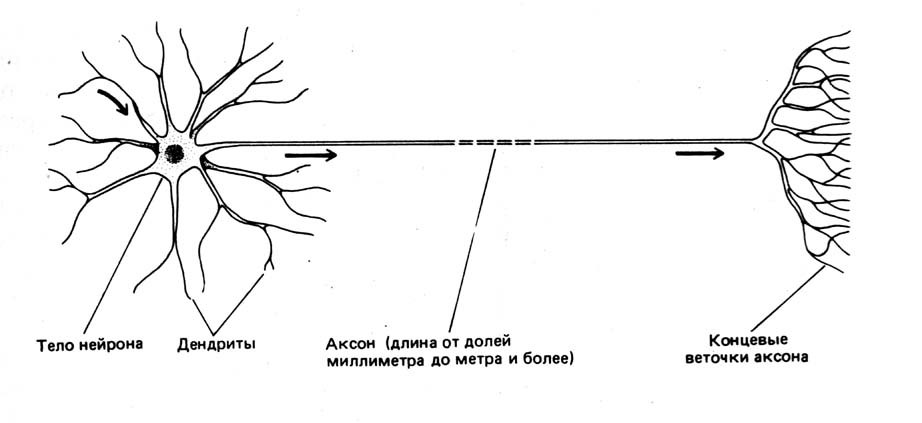
Рис.1 Схема нейрона

Нейронную сеть можно ввести как совокупность нейронов и их взаимосвязей. Следовательно, для того, чтобы определить искусственную (не биологическую) нейронную сеть необходимо:

Задать архитектуру сети;
Определить динамику отдельных элементов сети — нейронов;
Определить правила, по которым нейроны будут взаимодействовать между собой;
Описать алгоритм обучения, т.е. формирования связей для решения поставленной задачи.

Сеть состоит из N искусственных нейронов, аксон каждого нейрона связан с дендритами остальных нейронов, образуя обратную связь. Архитектура сети изображена на рис. 2.

Рис.2 Архитектура нейронной сети Хопфилда

Каждый нейрон может находиться в одном из 2-х состояний:

Динамика состояния во времени -ого нейрона в сети из нейронов описывается дискретной динамической системой:

где — матрица весовых коэффициентов, описывающих взаимодействие дендритов -ого нейрона с аксонами -ого нейрона.

Стоит отметить, что и случай не рассматриваются.

Обучение и устойчивость к шуму

Важной характеристикой нейронной сети является отношение числа ключевых образов , которые могут быть запомнены, к числу нейронов сети : . Для сети Хопфилда значение не больше 0.14.

Вычисление квадратной матрицы размера для ключевых образов производится по правилу Хебба:

где означает -ый элемент образа .

Стоит отметить, что в силу коммутативности операции умножения, соблюдается равенство

Уравнений (1), (2), (3), (4) достаточно для определения искусственной нейронной сети Хопфилда и можно перейти к ее реализации.

Реализация нейронной сети Хопфилда, определенной выше будет производиться на языке C++. Для упрощения экспериментов, добавим основные определения типов, напрямую связанных с видом нейрона и его передаточной функции в класс simple_neuron, а производные определим далее.

Самыми основными типами, напрямую связанными с нейроном являются:

тип весовых коэффициентов (выбран float);
тип, описывающий состояния нейрона (введен перечислимый тип с 2 допустимыми значениями).

На основе этих типов можно ввести остальные базовые типы:

тип, описывающий состояние сети в момент (выбран стандартный контейнер vector);
тип, описывающий матрицу весовых коэффициентов связей нейронов (выбран контейнер vector контейнеров vector).

Обучение сети, или, вычисление элементов матрицы в соответствии с (3) производится функцией learn_neuro_net, принимающей на вход список обучающих образов и возвращающей объект типа link_coeffs_t. Значения вычисляются только для нижнетреугольных элементов. Значения верхнетреугольных элементов вычисляются в соответствии с (4). Общий вид метода learn_neuro_net показан в листинге 2.

Обновление состояний нейронов реализовано с помощью функтора neuro_net_system. Аргументом метода _do функтора является начальное состояние , являющееся распознаваемых образом (в соответствии с (5)) — ссылка на объект типа neurons_line.

Метод функтора модифицирует передаваемый объект типа neurons_line до состояния нейронной сети в момент времени . Значение жестко не фиксировано и определяется выражением:

Для вычисления (2) применены 2 алгоритма STL:

std::inner_product для вычисления суммы произведений весовых коэффициентов и состояний нейронов (т.е. вычисление (2) для определенного );
std::transform для вычисления новых значений для каждого нейрона (т.е. вычисление пункта выше для каждого возможного )

Исходный код функтора neurons_net_system и метода calculate класса simple_neuron показан в листинге 3.

В репозитории проект CMake, из которого можно сгенерировать проект Visual Studio (VS2015 компилирует проект успешно) или обычные Unix Makefile’ы.

Сегодняшняя статья будет посвящена еще одному типу нейронных сетей, а именно дискретной сети Хопфилда, которая представляет из себя автоассоциативную сеть, способную выполнять функцию памяти. Но не буду забегать вперед, обо всем по порядку.

Итак, сразу же поговорим об основных задачах, которые призвана решать нейронная сеть Хопфилда. И основным ее применением является восстановление образца, ранее сохраненного сетью, по подаваемому на ее вход искаженному варианту. Вполне возможно на данном этапе это определение выглядит не совсем понятным, но сейчас все встанет на свои места. Пусть мы хотим сохранить при помощи сети Хопфилда цифры от нуля до девяти (о процессе сохранения мы поговорим чуть позже, пока не будем останавливаться на этом моменте). Рассмотрим, например, цифру 2, представленную в следующем виде:

Пусть сеть уже обучена, то есть эту цифру, как и остальные, мы сохранили в памяти. Тогда если мы подадим искаженный вариант сохраненной цифры на вход, сеть должна выдать нам правильное изображение сети (то которое мы сохранили при обучении, без искажений). К примеру, подаваемый на вход образец может иметь следующий вид:

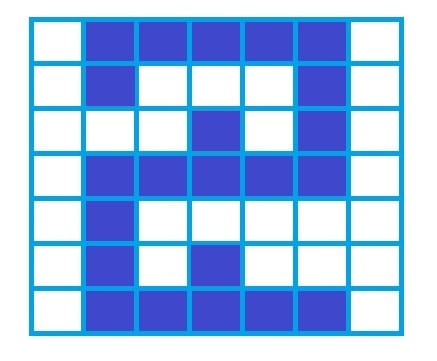
Вот, собственно, в этом и состоит задача нейронной сети Хопфилда. Давайте теперь обсудим структуру сети и непосредственно процесс обучения - запоминания образцов.

Сеть Хопфилда является однослойной - если не брать в расчет входные элементы. Каждый из нейронов связан со всеми остальными, но не воздействует на себя самого. В итоге получаем:

Здесь мы рассмотрели сеть с четырьмя нейронами.

Нейроны могут принимать два разных значения, но в отличие от ранее рассмотренных сетей, нейроны сети Хопфилда могут находиться в состояниях -1 и 1 (а не 0 и 1). Конечно, можно использовать и уже ставшую привычной систему состояний (0 и 1), но для сетей Хопфилда более традиционной является такая функция активности:

Комбинированный ввод вычисляется по формуле:

Здесь s_i - состояние нейрона с номером i . Если комбинированный ввод элемента оказывается отрицательным, то состояние элемента становится равным -1, напротив, когда комбинированный ввод положительный - состояние элемента соответствует +1. Если же net_j = 0 , то нейрон не изменяет своего состояния, то есть сохраняет предыдущее. Со структурой сети вроде разобрались, перейдем к процессу обучения.

Обучение нейронной сети Хопфилда значительно отличается от привычных алгоритмов обучения (например, от обучения по принципу обратного распространения ошибки). В случае сети Хопфилда процедура обучения для одного входного образца (процедура сохранения образца) представляет из себя просто расчет весовых коэффициентов по определенной формуле:

Где W - это матрица весов, x - входной образец, а x^T - транспонированный вектор x (получается из исходного вектора заменой строк на столбцы). Если мы хотим сохранить несколько образцов ( k ), то необходимо произвести вычисления по этой формуле для каждого из образцов по отдельности, а затем сложить полученные матрицы W_k :

Возможно сейчас еще нет полного понимания работы данных сетей, но мы обязательно разберем какой-нибудь практический пример, и тогда все окончательно прояснится 👍

Необходимо отметить еще один важный аспект обучения. Помните, в начале статьи мы говорили, что нейроны в сети Хопфилда не воздействуют сами на себя? Так вот, чтобы обеспечить выполнение этого условия, необходимо обнулить диагональные элементы в полученной в результате сохранения образцов матрице весов.

Итак, сеть обучена, осталось понять, как же она должна работать. В данном случае все довольно просто. Пусть мы подаем на вход искаженный элемент (например, цифру 2, которую мы уже обсуждали). В результате работы сети состояния нейронов начинают изменяться. И нам остается только ждать пока сеть перейдет в устойчивое состояние - то есть в результате последующих обновлений ни один из нейронов не будет изменять свое состояние.В результате всех этих процессов мы получим сохраненный (неискаженный) вариант подаваемого на вход образца (вектора). Вот, собственно, и все.

Еще одним моментом, на котором нельзя не остановиться, является вопрос, касающийся устойчивости сети, то есть ее способности остановиться на каком-то конечном состоянии (нейроны неустойчивой сети просто будут бесконечно менять свои состояния). Мы в этой статье ограничимся рассмотрением сетей, работающих в асинхронном режиме (это означает, что в каждый момент времени меняется состояние только одного нейрона). Введем понятие функции энергии системы:

При изменении состояния нейрона j на \Delta s_j энергия изменится на величину:

Под знаком суммы у нас тут комбинированный ввод элемента j . Таким образом, если комбинированный ввод положительный, то и изменение состояния нейрона j положительное ( \Delta s_j > 0 ). Аналогично, если \sum_^> , то и \Delta s_j . Поэтому изменение энергии всегда будет отрицательным (энергия будет уменьшаться в процессе работы сети), что и гарантирует нам то, что сеть является устойчивой.

Пожалуй, на этом закончим обсуждение теоретических аспектов и, как я и обещал, рассмотрим небольшой практический пример, который нам наглядно продемонстрирует обучение и работу нейронной сети Хопфилда.

Я решил привести пример из одной замечательной книги и выглядит он следующим образом. Пусть нашей задачей является сохранение образца x = [1, -1, 1, 1]. На первом этапе мы должны определить весовые значения сети Хопфилда, а во второй части примера мы убедимся, что сеть сможет восстановить сохраненный образец при подаче на вход искаженного вектора x_ = [-1, -1, 1, 1].

Определяем весовую матрицу по формуле W = x^Tx :

Не забываем о том, что нам надо обнулить диагональные элементы матрицы:

Весовые значения мы рассчитали, давайте подадим на вход вектор x_ и посмотрим, как поведут себя нейроны нашей сети. Комбинированный ввод первого нейрона будет равен:

Поскольку net_1 > 0 , то нейрон 1 будет находиться в состоянии +1 . Для второго нейрона:

Нейрон 2 окажется в состоянии -1 .

Таким образом, мы получили такой вектор: [1, -1, 1, 1], что соответствует тому образцу, который мы запоминали в первой части примера. Как видите, наша сеть работает. Если теперь еще раз произвести расчет состояний нейронов в соответствии с теми состояниями, которые они приняли после прохождения вектора x_ по взвешенным связям, то мы увидим, что состояние не изменится, то есть сеть оказалась в устойчивом положении.

На рассмотрении этого примера мы и закончим сегодняшнюю статью. Надеюсь материал окажется понятным и полезным 🤝

Нейронная сеть Хопфилда состоит из N искусственных нейронов. Каждый нейрон системы может принимать одно из двух состояний (что аналогично выходу нейрона с пороговой функцией активации):

$<\displaystyle x_ =\left\1,\\-1\end>\right.>$

Благодаря своей биполярной природе нейроны сети Хопфилда иногда называют

$<\displaystyle w_<ij> В сети Хопфилда матрица связей является симметричной =w_>$
, а диагональные элементы матрицы полагаются равными нулю ( =0>" width="" height="" />
), что исключает эффект воздействия нейрона на самого себя и является необходимым для сети Хопфилда, но не достаточным условием, устойчивости в процессе работы сети. Достаточным является асинхронный режим работы сети. Подобные свойства определяют тесную связь с реальными физическими веществами называемыми Обучение сети [ ]

$<\displaystyle X_ Алгоритм обучения сети Хопфилда имеет существенные отличия в сравнении с такими классическими алгоритмами обучения перцептронов как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе. Вычисление коэффициентов базируется на следующем правиле: для всех запомненных образов >$
матрица связи должна удовлетворять уравнению

$<\displaystyle X_ ^=WX_>$

$<\displaystyle X_ поскольку именно при этом условии состояния сети >$
будут устойчивы - попав в такое состояние, сеть в нем и останется.

Некоторые авторы относят сеть Хопфилда к обучению без учителя. Но это неверно, т.к. обучение без учителя предполагает отсутствие информации о том, к каким классам нужно относить стимулы. Для сети Хопфилда без этой информации нельзя настроить весовые коэффициенты, поэтому здесь можно говорить лишь о том, что такую сеть можно отнести к классу оптимизирующих сетей (фильтров). Отличительной особенностью фильтров является то, что матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются. Это может быть удобно для физического воплощения такого устройства, т.к. на схемотехническом уровне реализовать устройство с переменными весовыми коэффициентами на порядок сложнее. Примером фильтра без обратных связей может служить алгоритм CC4 (Cornel classification), автором которого является S.Kak.

В сети Хопфилда есть обратные связи и из-за этого нужно решать проблему устойчивости. Веса между нейронами в сети Хопфилда могут рассматриваться в виде матрицы взаимодействий W. В работе [1] показано, что сеть с обратными связями является устойчивой, если ее матрица симметрична и имеет нули на главной диагонали. Имеется много устойчивых систем, например, все сети прямого распространения, а так же современные рекуррентные сети Джордана и Элмана, для которых не обязательно выполнять условие на симметрию. Но это происходит вследствие того, что на обратные связи наложены другие ограничения. В случае сети Хопфилда условие симметричности является необходимым, но не достаточным, в том смысле, что на достижение устойчивого состояния влияет еще и режим работы сети. Ниже будет показано, что только асинхронный режим работы сети гарантирует достижение устойчивого состояния сети, в синхронном случае возможно бесконечное переключение между двумя разными состояниями (такая ситуация называется динамическим аттрактором, в то время как устойчивое состояние принято называть статическим аттрактором).

Запоминаемые векторы должны иметь бинарный вид. После этого происходит расчет весовых коэффициентов по следующей формуле :

$<\displaystyle w_<ij> =>\sum _X_X_>$

$<\displaystyle X_<ij> где N - размерность векторов, m – число запоминаемых выходных векторов; d – номер запоминаемого выходного вектора; >$
– i-я компонента запоминаемого выходного j-го вектора.

Это выражение может стать более ясным, если заметить, что весовая матрица W может быть найдена вычислением внешнего произведения каждого запоминаемого вектора с самим собой и суммированием матриц, полученных таким образом. Это может быть записано в виде

$<\displaystyle W=<\frac <1> >\sum _X_^X_>$

$<\displaystyle X_ где >$
– i-й запоминаемый вектор-строка.

Расчет этих весовых коэффициентов и называется обучением сети.

Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным. Для этого выходам сети сначала придают значения этого начального вектора. Затем сеть последовательно меняет свои состояния согласно формуле:

$<\displaystyle X_<i+1> ^=F(WX_)>$

где F - активационная функция, >" width="" height="" />
и >" width="" height="" />
- текущее и следующее состояния сети, до тех пор, пока состояния >" width="" height="" />
и >" width="" height="" />
не совпадут (или, в случае синхронного режима работы, не совпадут состояния >" width="" height="" />
с >" width="" height="" />
и одновременно >" width="" height="" />
с >" width="" height="" />
). Именно этот процесс называется конвергенцией сети. Полученное устойчивое состояние >" width="" height="" />
(статический аттрактор), или, возможно, в синхронном случае пара >" width="" height="" />
> (динамический аттрактор), является ответом сети на данный входной образ.

Работа сети в режиме фильтрации (восстановление повреждённых образов) [ ]

Пороговая функция, реализуемая нейроном сети Хопфилда.

Так как сети с обратными связями имеют пути, передающие сигналы от выходов к входам, то отклик таких сетей является динамическим, т. е. после приложения нового входа вычисляется выход и, передаваясь по сети обратной связи, модифицирует вход. Затем выход повторно вычисляется, и процесс повторяется снова и снова. Для устойчивой сети последовательные итерации приводят к все меньшим изменениям выхода, пока в конце концов выход не становится постоянным. Для некоторых сетей процесс никогда не заканчивается, такие сети называют неустойчивыми. Проблема устойчивости будет рассмотрена в следующем разделе, а здесь мы рассмотрим основной цикл работы сети.

$<\displaystyle ~X(t+1)^<T> =F(WX(t))>$

где F - активационная функция, " width="" height="" />
и " width="" height="" />
- текущее и следующее состояния сети, до тех пор, пока состояния " width="" height="" />
и " width="" height="" />
не совпадут (или, в случае синхронного режима работы, не совпадут состояния " width="" height="" />
с " width="" height="" />
и одновременно " width="" height="" />
с " width="" height="" />
). Именно этот процесс называется конвергенцией сети.

Это же можно описать так называемым локальным полем >" width="" height="" />
действующим на нейрон >" width="" height="" />
со стороны всех остальных нейронов сети: (t)=\sum _^w_x_(t-1)>" width="" height="" />
.

После расчета локального поля нейрона (t)>" width="" height="" />
это значение используется для расчета значения выхода через функцию активации, которая в данном случае является пороговой (с нулевым порогом). Соответственно, значение выхода нейрона i в текущий момент времени (t)>" width="" height="" />
расчитывается по формуле: (t)=sign(\sum _^w_x_(t-1))>" width="" height="" />
, где

$<\displaystyle w_<ij> >$
- весовой коэффициента между нейронами i и j, (t-1)>" width="" height="" />
- значения выходов нейрона j в предыдущий момент времени.

$<\displaystyle X(t)> Во время работы сети Хопфилда признаком нахождения решения является момент, когда достигается аттрактор, статический (когда на каждом следующем шаге повторяется устойчивое состояние$
) или, возможно, динамический (когда до бесконечности чередуются два разных состояния < " width="" height="" />
>). Это конечное состояние сети и является ее реакцией на данный образ.

Обычно ответом является такое устойчивое состояние, которое совпадает с одним из запомненных при обучении векторов, однако при некоторых условиях (в частности, при слишком большом количестве запомненных образов) результатом работы может стать так называемый ложный аттрактор ("химера"), состоящий из нескольких частей разных запомненных образов, а также в синхронном режиме сеть может прийти к динамическому аттрактору. Обе эти ситуации в общем случае являются нежелательными, поскольку не соответствуют ни одному запомненному вектору - а соответственно, не определяют класс, к которому сеть отнесла входной образ.

Для сети Хопфилда могут существовать две модификации отличающиеся по времени передачи сигнала: асинхронный и синхронный режимы.

Синхронный режим работы сети [ ]

Если работа сети моделируется на одном процессоре, то при синхронном режиме последовательно просматриваются нейроны, однако их состояния запоминаются отдельно и не меняются до тех пор, пока не будут пройдены все нейроны сети. Когда все нейроны просмотрены, их состояния одновременно (т.е. синхронно, отсюда и название) меняются на новые. Таким образом, достигается моделирование параллельной работы последовательным алгоритмом. При реально параллельном моделировании, этот режим фактически означает, что время передачи >" width="" height="" />
для каждой связи между элементами >" width="" height="" />
и >" width="" height="" />
одинаковое для каждой связи, что приводит к параллельной работе всех связей, они одновременно меняют свои состояния, основываясь только на предыдущем моменте времени. Наличие таких синхронных тактов, которые можно легко выделить и приводит к пониманию синхронного режима. При синхронном режиме возможно (хотя и далеко не всегда наблюдается) бесконечное чередование двух состояний с разной энергией - так называемый динамический аттрактор. Поэтому синхронный режим практически для сети Хопфилда не используется, и рассматривается лишь как основа для понимания более сложного асинхронного режима.

Асинхронный режим работы сети [ ]

Если моделировать работу сети как последовательный алгоритм, то в асинхронном режиме работы состояния нейронов в следующий момент времени меняются последовательно: вычисляется локальное поле для первого нейрона в момент t, определяется его реакция, и нейрон устанавливается в новое состояние (которое соответствует его выходу в момент t+1), потом вычисляется локальное поле для второго нейрона с учетом нового состояния первого, меняется состояние второго нейрона, и так далее - состояние каждого следующего нейрона вычисляется с учетом всех изменений состояний рассмотренных ранее нейронов.

По сути при последовательной реализации сети Хопфилда явно не видно в чем заключается асинхронность, но это видно если сеть Хопфилда реализовать с параллельными вычислениями. В этом случае асинхронный режим сети Хопфилда упрощен, и носит частный случай по сравнению с общим видом асинхронных сетей, где время передачи >" width="" height="" />
для каждой связи между элементами >" width="" height="" />
и >" width="" height="" />
свое, но постоянное. Чтобы рассмотреть работу сети при параллельной реализации, необходимо ввести понятие такта - как минимальное время за которое происходит передача сигнала по связи, т.е. при =1>" width="" height="" />
. Тогда за промежуток времени между t и (t+1) происходит определенное количество тактов N. И именно в пределах времени из N тактов происходит асинхроность протекания сигналов и выполнения расчетов. То есть, например, когда нужно расчитать состояние нейрона №3 необходимо расчитать состояния нейрона №1 и состояния нейрона №2 и умножить это на соответствующие веса w13 и w23. Но оказывается, для того чтобы расчитать состояние нейрона №2 нам нужно знать обновленное состояние нейрона №1 и старое состояние нейрона №3, умножить их на веса w12 и w32. Понятно, что физически не возможно расчитать состояние нейрона №1 и состояние нейрона №2 за одно и то же время, т.к. состояние нейрона №2 зависит от состония нейрона №1. Поэтому связь между нейроном №1 и нейроном №3 имеете время передачи =2>" width="" height="" />
, и достигает нейрона №3 за два такта. Именное такое разное время передачи >" width="" height="" />
и позволяет говорить о сети Хопфилда как о сети с ассинхроным режимом.

В асинхронном режиме невозможен динамический аттрактор - вне зависимости от количества запомненных образов и начального состояния, сеть непременно придет к устойчивому состоянию (статическому аттрактору).

Пример востановления повреждённого изображения [ ]

Если во время обучения сформировать матрицу весовых коэффициентов (межнейронных связей) на основании эталонных бинарных векторов, то нейронная сеть в процессе работы под действием описанных выше полей будет менять состояния нейронов до тех пор, пока не перейдет к одному из устойчивых состояний.

Пусть имеется нейронная сеть размерностью N=100 , в матрицу связей записан набор черно-белых картинок (-1 — черный цвет, +1 — белый), среди которых есть изображение собачки (рис 1б). Если установить начальное состояние сети близким к этому вектору (рис. 1а), то в ходе динамики нейронная сеть восстановит исходное изображение (рис. 1б). В этом смысле можно говорить о том, что сеть Хопфилда решает задачу распознавания образов (хотя строго говоря, полученное эталонное изображение еще нужно превратить в номер класса, что в некоторых случаях может быть весьма вычислительно емкой задачей).

Устойчивость сети в процессе работы [ ]

Принципиальная разница между двумя режимами работы сети состоит в том, что в асинхронном случае сеть обязательно придет к одному устойчивому состоянию. При синхронном же возможны ситуации с бесконечным циклическим переходом между двумя разными состояниями.

Определить устойчиво или нет состояние нейрона можно на основании, так называемой искусственной энергии нейрона в данном поле =-s_h_>" width="" height="" />
. Если знак выхода (+1 или -1) нейрона совпадает с направлением локального поля (), то его положение энергетически устойчиво и в последующий момент времени состояние нейрона остается неизменным. В противном случае () положение нейрона неустойчиво и он меняет свой знак, переходя в состояние (t+1)=-s_(t)>" width="" height="" />
с энергией .

Устойчивость при асинхроном способе достигается потому, что выполняется условие на общую энергию сети " width="" height="" />
, в синхронном случае условие несколько изменяется, а именно: " width="" height="" />
. В ситуации когда происходит бесконечные циклические переходы энергия двух разных состоянияй соответственно равна " width="" height="" />
и " width="" height="" />
. При этом состояния " width="" height="" />
и " width="" height="" />
, а также " width="" height="" />
и " width="" height="" />
— совпадают. Если образуется такое состояние, то его называется динамическим аттрактором. Если же совпадают состояния " width="" height="" />
и " width="" height="" />
, аттрактор называют статическим. В большинстве случаев динамические аттракторы являются нежелательными, так как не соответствуют какому-либо определенному ответу сети.

Ассоциативная память [ ]

Задачи минимизации [ ]

Однако обработка визуальных образов (фильтрация и ассоциативная память) — не единственная область применения модели Хопфилда. Динамическая процедура, описанная выше, на каждом шаге понижает значение энергии нейронной сети. Это позволяет решать Ограничения сети [ ]

К сожалению, у нейронной сети Хопфилда есть ряд недостатков.

1. Относительно небольшой объем памяти, величину которого можно оценить выражением:

$<\displaystyle M\approx \;<\frac <N> <2\log _<2>N>>>$

Попытка записи большего числа образов приводит к тому, что нейронная сеть перестает их распознавать.

2. Достижение устойчивого состояния не гарантирует правильный ответ сети. Это происходит из-за того, что сеть может сойтись к так называемым ложным аттракторам, иногда называемым "химерой" (как правило, химеры склеены из фрагментов различных образов).

Нейронная сеть Хопфилда — полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия являются локальными минимумами функционала, называемого энергией сети (в простейшем случае — локальными минимумами отрицательно определённой квадратичной формы на n-мерном кубе). Такая сеть может быть использована как автоассоциативная память, как фильтр, а также для решения некоторых задач оптимизации. В отличие от многих нейронных сетей, работающих до получения ответа через определённое количество тактов, сети Хопфилда работают до достижения равновесия, когда следующее состояние сети в точности равно предыдущему: начальное состояние является входным образом, а при равновесии получают выходной образ. (с) Википедия

Предположим, мы имеем определённое количество начальных образов – изображений, либо чего-нибудь ещё. Нам предлагают видоизменённый образ, и задача наша состоит в распознании одного из эталонных шаблонов. Как это сделает человек – вопрос довольно сложный. А вот как с подобной задачей справится нейронная сеть – такое вполне можно представить. Особенно если это нейронная сеть Хопфилда.

Данной статье была убрана вся математика и большая часть терминологии, это может показаться неправильным, однако, я думаю, это поможет лучше осознать основную идею. Так же будет предложен пример на Python, чтобы визуально продемонстрировать работу системы.

Следующим пунктом мы взглянем на программную реализацию процесса формирования нейронной сети Хопфилда, назначение которой служит распознавание образов. Она была предложена Джоном Хопфилдом в 1984 году. На данный момент разработаны множественные её модификации, но сейчас мы будем рассматривать именно оригинальную модель.

Каким образом нейроны между собой связаны, зависит от того какой тип сети мы строим. Каждый сетевой нейрон передаёт и получает сигналы от другим. Сеть Хопфилда – это однослойная сеть, так как она использует только один слой нейронов. Так же она является рекурсивной сетью, и обладает обратными связями. Функции сети являются циклическми, то есть постоянно повторяются. Ниже показан пример сети Хопфилда в котором задействовано 4 нейрона. Все они имеют выходы сигнала, которые связываются с выходами всех нейронов, кроме себя:

К сожалению такую сеть ничему практически обучить нельзя. Для этого нам потребуется намного больше нейронов. Сеть, в которой содержится N нейронов запоминает не более ~0.15*N различных образов. Поэтому рабочая сеть должна использовать достаточно большое количество нейронов. Одно из самых больших недостатков подобной сети – это низкая ёмкость. К тому же образы не должны сильно походить друг на друга, так как иногда это может вызвать цикличность при распознавании.

Как работает сеть

Образы, которые сеть распознаёт или запоминает представляется вектором который имеет размерность X и n, где n – это число нейронов задействованных в сети. Выходной же образ будет вектором Y с идентичной размерностью. Каждый вектор будет принимать значения: -1 или +1. Можно конечно использовать и 0 с 1, но первый вариант немного удобнее для расчётов.

Естественно, в программной реализации работать непосредственно с нейронами мы не будем, а будем эмулировать их работу при помощи матрицы коэффициентов и векторов.

Обучение сети

Как было ранее сказано, сеть будет строится на вычислении коэффициентов весов. Для этого мы создадим матрицу W с рразмером азмером n x n. При обучении сети некому образу X коэффициенты устанавливаются так:

Читайте также: