Линейная регрессия кратко и понятно

Обновлено: 04.07.2024

Линейный регрессионный анализ используется для прогнозирования значения переменной на основе значения другой переменной. Переменная, которую требуется предсказать, называется зависимой переменной. Переменная, которая используется для предсказания значения другой переменной, называется независимой переменной.

Эта форма анализа заключается в подборе таких коэффициентов линейного уравнения с одной или несколькими независимыми переменными, чтобы это уравнение наилучшим образом предсказывало значение зависимой переменной. Результат линейной регрессии может быть представлен в виде прямой на плоскости, минимизирующей расхождение между прогнозируемыми и фактическими значениями. Существуют простые калькуляторы линейной регрессии, в которых для расчета оптимальной прямой для аппроксимации набора данных используется метод наименьших квадратов. После этого выполняется оценка величины X (зависимой переменной) по величине Y (независимой переменной).

Простота прогнозирования

Расчет линейной регрессии с помощью Microsoft Excel или статистических пакетов, например IBM SPSS® Statistics, значительно упрощает работу с уравнениями, моделями и формулами линейной регрессии. SPSS Statistics может применяться для расчета простой и множественной линейной регрессии.

Линейной регрессией можно пользоваться в разнообразных программах и средах, например:

Линейная регрессия в R
Линейная регрессия в MATLAB
Линейная регрессия в Sklearn
Линейная регрессия в Python
Линейная регрессия в Excel

Почему линейная регрессия важна

Модели линейной регрессии сравнительно просты и предлагают простые для понимания математические формулы прогнозирования. Линейная регрессия может применяться в разных областях науки и бизнеса.

Линейная регрессия используется повсюду: в биологии, исследованиях поведения и окружающей среды, в обществознании и бизнесе. Модели линейной регрессии зарекомендовали себя в качестве надежного научного метода прогнозирования будущего. Поскольку линейная регрессия представляет собой хорошо изученную статистическую процедуру, свойства моделей линейной регрессии хорошо понятны и просты в обучении.

Надежный научный метод прогнозирования будущего.

Руководители могут пользоваться линейной регрессией для повышения качества принимаемых решений. Организации собирают большие объемы данных, и линейная регрессия помогает им пользоваться этими данными вместо опыта и интуиции для оптимизации взаимодействия с окружающей реальностью. Таким образом, появляется возможность трансформировать большие объемы данных в полезную информацию.

Линейной регрессией также можно пользоваться для повышения качества информации путем анализа закономерностей и взаимосвязей, которые ваши коллеги уже видели и думают, что понимают. Например, анализ данных о продажах и закупках помогает выявить закономерности в покупках в определенные дни недели или время суток. Информация, полученная с помощью регрессионного анализа, помогает прогнозировать периоды времени, когда продукция их компании будет пользоваться высоким спросом.

Основные допущения эффективной линейной регрессии

Допущения, которые следует принимать во внимание в ходе линейного регрессионного анализа:

Для каждой переменной: Примите во внимание количество допустимых случаев, среднее значение и стандартное отклонение.
Для каждой модели: Примите во внимание коэффициенты регрессии, матрицу корреляции, частичные корреляции, множественный коэффициент корреляции, коэффициент детерминации, скорректированный коэффициент детерминации, изменение коэффициента детерминации, стандартную ошибку оценки, таблицу анализа дисперсии, спрогнозированные значения и ошибки. Также следует принять во внимание 95%-е доверительные интервалы для каждого коэффициента регрессии, матрицы дисперсии и ковариации, фактор роста дисперсии, толерантность, критерий Дарбина-Уотсона, меры расстояния (Махаланобис, Кук и значения рычагов), DfBeta, DfFit, интервалы прогнозирования и диагностическую информацию по каждому конкретному случаю.
Диаграммы: Примите во внимание диаграммы рассеяния, частичные диаграммы, гистограммы и диаграммы нормального распределения.
Данные: Зависимые и независимые переменные должны быть числовыми. Категорийные данные, например религия, профильное образование или регион проживания, должны сохраняться в двоичных переменных или других переменных, допускающих сравнение.
Другие предположения: Для каждого значения независимой переменной распределение зависимой переменной должно быть нормальным. Дисперсия распределения зависимой переменной должна быть постоянной для всех значений независимой переменной. Связь между зависимой переменной и каждой независимой переменной должна быть линейной, и все наблюдения должны быть независимыми.

Убедитесь, что ваши данные соответствуют допущениям линейной регрессии.

Прежде чем выполнять линейную регрессию, необходимо убедиться, что ваши данные поддаются анализу этим методом. Данные должны соответствовать определенным допущениям.

Как проверить выполнение этих допущений:

Переменные должны измеряться непрерывно. Примеры непрерывных переменных: время, продажи, вес, результаты тестов.
С помощью диаграммы рассеяния можно быстро определить, имеется ли линейная взаимосвязь между двумя переменными.
Наблюдения должны быть независимыми друг от друга.
В данных не должно быть значительных выбросов.
Проверьте данные на гомоскедастичность — однородность дисперсии случайной ошибки регрессионной модели.
Дисперсия случайной ошибки регрессионной модели должна иметь нормальное распределение.

Примеры эффективной линейной регрессии

Оценка тенденций и продаж

Линейным регрессионным анализом также можно пользоваться для прогнозирования годовых продаж (зависимая переменная) по таким независимым переменным, как возраст, образование и количество лет опыта.

Анализ эластичности цен

Изменение цен часто влияет на поведение потребителей, и линейная регрессия помогает проанализировать это влияние. Например, если цены на определенный продукт постоянно меняются, регрессионный анализ позволяет понять, падает ли потребление при росте цены. Что если потребление не будет значительно сокращаться при увеличении цены? При какой цене покупатели перестают покупать продукт? Эта информация очень пригодится руководителям предприятий розничной торговли.

Оценка рисков в страховой компании

Линейной регрессией можно пользоваться для анализа рисков. Например, у страховой компании может быть ограниченный объем ресурсов для расследования страховых случаев, связанных с недвижимым имуществом. С помощью линейной регрессии можно создать модель оценки стоимости страховых случаев. Этот анализ может помочь руководителям компании принимать важные решения о том, какие риски готова принимать компания.

Спортивный анализ

Сферы применения линейной регрессии не ограничены бизнесом. Она также важна в спорте. Например, можно заинтересоваться вопросом о том, зависит ли количество матчей, выигранных баскетбольной командой за сезон, от среднего количества очков за матч. По диаграмме рассеяния видно, что между этими переменными существует линейная зависимость. Количество выигранных матчей и среднее количество очков, набранное противником, также демонстрируют линейную корреляцию. У этих переменных корреляция отрицательная. С увеличением количества выигранных матчей уменьшается среднее количество очков, набранных оппонентом. С помощью линейной регрессии можно смоделировать взаимосвязь этих переменных. Хорошая модель позволяет спрогнозировать количество матчей, которое выиграет команда.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова "регрессия" исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей "регрессировал" и "двигался вспять" к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

Остатки нормально распределены с нулевым средним значением;

Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

"Влиятельное" наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть "влиятельным" наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для "влиятельных" наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

- оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся "внутри диапазона."

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.

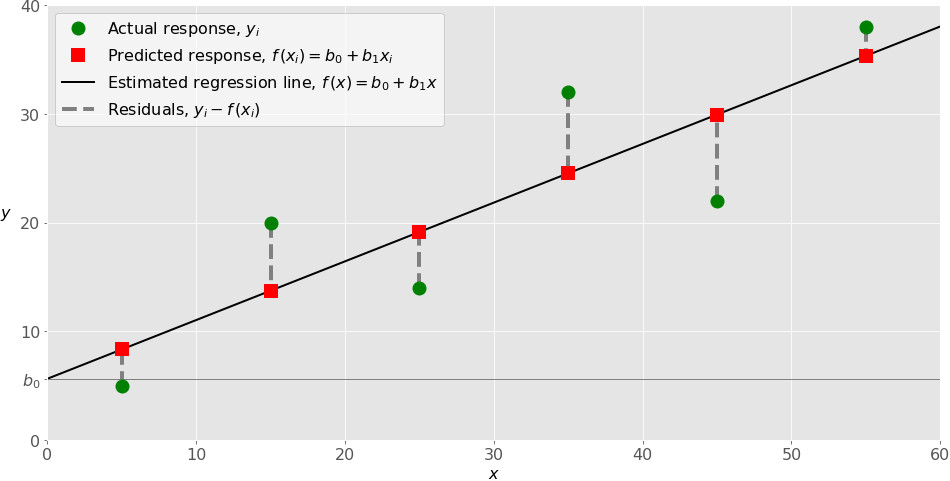
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.

Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

Импортируйте необходимые пакеты и классы.
Предоставьте данные для работы и преобразования.
Создайте модель регрессии и приспособьте к существующим данным.
Проверьте результаты совмещения и удовлетворительность модели.
Примените модель для прогнозов.

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :

Теперь у вас есть весь функционал для реализации линейной регрессии.

Фундаментальный тип данных NumPy – это тип массива numpy.ndarray . Далее под массивом подразумеваются все экземпляры типа numpy.ndarray .

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape() на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).

Вот как x и y выглядят теперь:

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Давайте сделаем экземпляр класса LinearRegression , который представит модель регрессии:

Эта операция создаёт переменную model в качестве экземпляра LinearRegression . Вы можете предоставить несколько опциональных параметров классу LinearRegression :

fit_intercept – логический ( True по умолчанию) параметр, который решает, вычислять отрезок b₀ ( True ) или рассматривать его как равный нулю ( False ).
normalize – логический ( False по умолчанию) параметр, который решает, нормализовать входные переменные ( True ) или нет ( False ).
copy_X – логический ( True по умолчанию) параметр, который решает, копировать ( True ) или перезаписывать входные переменные ( False ).
n_jobs – целое или None (по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях. None означает отсутствие процессов, при -1 используются все доступные процессоры.

Наш пример использует состояния параметров по умолчанию.

Пришло время задействовать model . Сначала вызовите .fit() на model :

С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self - переменную model . Поэтому можно заменить две последние операции на:

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

Вы можете получить определения (R²) с помощью .score() , вызванной на model :

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².

model содержит атрибуты .intercept_ , который представляет собой коэффициент, и b₀ с .coef_ , которые представляют b₁:

Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.

Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Получите предсказанный ответ, используя .predict() :

Применяя .predict() , вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.

Вот почти идентичный способ предсказать ответ:

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1) , x.flatten() или x.ravel() при умножении с помощью model.coef_ .

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new . Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.

Зависимую переменную в бизнесе называют предиктором (характеристика, за изменением которой наблюдают). Это может быть уровень продаж, риски, ценообразование, производительность и так далее. Независимые переменные — те, которые могут объяснять поведение выше приведенных факторов (время года, покупательная способность населения, место продаж и многое другое).Регрессионный анализ включает несколько моделей. Наиболее распространенные из них: линейная, мультилинейная (или множественная линейная) и нелинейная.

Как видно из названий, модели отличаются типом зависимости переменных: линейная описывается линейной функцией; мультилинейная также представляет линейную функцию, но в нее входит больше параметров (независимых переменных); нелинейная модель — та, в которой экспериментальные данные характеризуются функцией, являющейся нелинейной (показательной, логарифмической, тригонометрической и так далее).

Чаще всего используются простые линейные и мультилинейные модели.

Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы.

Рассмотрим поподробнее принципы построения и адаптации результатов метода.

Линейный регрессионный анализ основан на шести фундаментальных предположениях:

Читайте также: