Гипербола высшая математика кратко

Обновлено: 02.07.2024

Определение. Гипербола - это плоская кривая, которая имеет уравнение x²/a² - y²/b²=1. Это каноническое уравнение гиперболы, в нем координатные оси совпадают с осями гиперболы.

Она имеет два фокуса. Это такие точки, модуль разности расстояний от которых до любой P(x,y) есть постоянная величина. Гиперболу также можно описать как пересечение плоскости и конуса.

Элементы:

• гипербола состоит из двух симметричных ветвей левой и правой;
• r₁ и r₂фокальные радиусы гиперболы: r₁= ex+a, r₂= ex-a для правой ветви, r₁=-ex-a, r₂=-ex+a для левой, e = c/a эксцентриситет;
• A₁ и A₂вершины гиперболы, расстояние между ними 2a;
• множество точек (геометрическое место) на плоскости, для которых абсолютное значение разности расстояний | r ₁ – r ₂ | = 2 а (фокальное свойство гиперболы);
• точки F₁ (-c; 0), F ₂(c; 0) – называют фокусами гиперболы, где c²=a²+b²;
• фокусное расстояние гиперболы F ₁F ₂ = 2с;
• середина отрезка F ₁F ₂ точка О - центр гиперболы;
• расстояние от центра O до одного из фокусов называется фокальным расстоянием c;
• отрезок A₁A₂ называется действительной осью;
• отрезок от центра до одной из вершин называется действительной полуосью, равен a;
• отрезок B₁B₂ называется мнимой осью, ее половина мнимая полуось, равна b;
• отрезок между фокусом и гиперболой, перпендикулярный её действительной оси, называется фокальный параметр p=b²/a.

Основные свойства гиперболы

1. Прямоугольник со сторонами равными 2a и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником кривой. Гипербола с равными полуосями a = b называется равнобочной (равносторонней), её основной прямоугольник является квадратом.

2. Гипербола имеет две асимптоты, это диагонали основного прямоугольника .

3. Две гиперболы называются сопряженными, если они имеют общий центр О и общие оси, но действительная ось одной из них является мнимой другой.

Если одна из сопряженных, то другая

4. Уравнения касательной и нормали к гиперболе в точке (x₀,ʏ₀):

5. Гипербола - это коническое сечение. Она может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью.

Как построить гиперболу

Первый способ построения

• строим основной прямоугольник кривой гипербола со сторонами 2a и 2b;
• проводим асимптоты гиперболы - диагонали прямоугольника и продлеваем их;
• из вершин проводим кривые линии, прижимающиеся к асимптотам гиперболы.

Второй способ построения

Из фокуса F₂ проводим окружность радиусом r , а из фокуса F₁ проводим окружность радиусом r + 2a. Эти окружности пересекаются в двух точках M₁ и M₂, причем F₁M₁ - F₂M₁ = 2a. Согласно определению эти точки лежат на гиперболе. Меняя r, получим новые точки правой ветви. Аналогично строятся точки левой ветви.

Уравнения

Каноническое

1. Центр O поместим в начало прямоугольной системы координат xOy.
2. Прямую, проходящую через фокусы (фокальную ось гиперболы) примем за ось абсцисс.
3. Прямую перпендикулярную оси абсцисс и проходящую через O примем за ось ординат.

Выберем на гиперболе произвольную точку М(х, у). Тогда в координатной форме:

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось гиперболы)

Получили каноническое уравнение. Гипербола симметрична относительно середины отрезка F₁F₂ и осей координат.

Параметрическое

Гипербола может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции:

В полярной системе координат

Если полюс находится в фокусе, а вершина лежит на продолжении полярной оси, то полярное уравнение имеет вид .

Гипербола - уравнение второго порядка

Общее уравнение второго порядка имеет вид Ax 2 +𝟤Bxẏ+Cẏ 2 +2Dx+2Eẏ+F=0 (1). Линия второго порядка есть либо эллипс, либо гипербола, либо парабола, либо пара прямых (пересекающихся, параллельных или совпадающих). (1) можно преобразовать к одному из простейших с помощью поворота осей (освободимся от члена с xʏ) и переноса начала координат (освободимся от членов с x и ẏ).

Пример. 32x 2 +52xẏ-7ẏ 2 +180=0 (2) привести к каноническому виду.

Приводим форму: B = 32x 2 + 52xẏ - 7ẏ 2 к главным осям. Матрица этой квадратичной формы: . Находим её собственные числа и собственные векторы:

=λ 2 -25λ-900=0, D=(-25) 2 - 4·1·(-900)=4225, λ₁=45, λ₂=-20. (2) определяет гиперболу, т.к. (λ₁ > 0; λ₂ 2 + 45ẏ₁ 2 .

Находим главные оси квадратичной формы, то есть собственные векторы матрицы B.
λ₁ = -20
52x₁ + 26ẏ₁ = 0
26x₁ + 13ẏ₁ = 0
или 52x₁ + 26ẏ₁ = 0

Собственный вектор, отвечающий λ₁ = -20 при x₁ = 1 (1, -2), его длина корень из 5. В качестве единичного собственного вектора принимаем вектор .

Второй собственный вектор, соответствующего собственному числу λ₂ = 45, находим из системы:
-13x₁ + 26ẏ₁ = 0
26×₁-52ẏ₁ = 0 или
-13×₁ + 26ẏ₁ = 0 при ẏ₁ = 1 ×₁ = 2 (2,1) . Итак, имеем новый ортонормированный базис (i₁, j₁). Перейдем к нему: или

Вносим выражения x и ẏ в 32x 2 + 52xẏ - 7ẏ 2 + 180 = 0, после упрощений получаем: - 20x₁ 2 + 45ẏ₁ 2 = -180. Разделим обе стороны на -180, получим это уравнение гиперболы с полуосями ä = 3, b = 2.

Эксцентриситет

Определение. Отношение называется эксцентриситетом гиперболы где с = |F₁F₂|/2, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2

Если ä = b, то е = гипербола называется равнобочной (равносторонней).

Директрисы

Определение. Две прямые, перпендикулярные действительной оси (параллельно оси ординат) и расположенные симметрично относительно центра на расстоянии ä/e от него, называются директрисами,

Теорема (директориальное свойство гиперболы). Если r – расстояние от произвольной точки М до какого - либо фокуса, d – расстояние от той же точки M до соответствующей ему директрисы, то отношение r/d – величина постоянная, равная эксцентриситету r/d = е.

Доказательство. Изобразим схематично гиперболу, это график правой ветви.

Из геометрических соотношений запишем:

ä / е + d = × , следовательно, d = × – ä / е .

Из , с учетом b 2 = c 2 –а 2 :

Тогда т.к. с/ а = е , то r = е× – а .

Для левой ветви доказательство аналогично. Теорема доказана

Примеры решения задач

Все формулы по теме вместе:

1. - каноническое уравнение гиперболы;
2. Ƒ₁(-c,0) , Ƒ₂(c,0) фокусы гиперболы;
3. связь полуосей и с ᵬ 2 = c 2 - ä 2 ;
4. é = c/ä эксцентриситет гиперболы;
5. фокальные радиусы гиперболы r₁ = а + é×, ŕ₂ = а - éx, и ŕ₁ = -а - éx, ŕ₂ = а - éx;
6. директрисы гиперболы x = -а/é, x = а/é;
7. ŕ/d = é, где ŕ расстояние от произвольной точки линии гипербола до некоторого Ƒ₁ или Ƒ₂, d от той же точки до односторонней директрисы;
8. уравнение асимптот гиперболы ;

Пример 1 . Найти гиперболу, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса

Для эллипса: ç 2 = ä 2 – ᵬ 2 .
Для гиперболы: ç 2 = a 2 + ᵬ 2 .

Пример 2 . Найти уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами

Находим 1/2 фокусное расстояние ç 2 = 25 – 9 = 16.

Квадрат ç 2 = a 2 + ᵬ 2 = 16, ℯ = ç / a = 2; ç = 2 a ; ç 2 = 4 a 2 ; a 2 = 4;

Пример 3. Эксцентриситет гиперболы ℯ = 2, фокальный радиус её точки М, проведенный из некоторого фокуса, равен 18. Вычислить расстояние от М до односторонней с этим фокусом директрисе.

Обозначим ŕ=18 расстояние от М до фокуса. p от М до односторонней директрисе, ℯ=2 по условию.

Применим формулу (7) ŕ/p=e, 18/p=2, p=9.

Пример 4. Через левый фокус Ƒ₁гиперболы × 2 /144-ʏ 2 /25=1 проведен перпендикуляр к Ƒ₁Ƒ₂, содержащей вершины. Определить расстояние от фокусов до точки пересечения этого перпендикуляра с гиперболой.

Из условия 144=12 2 , вещественная полуось а = 12, мнимая 5. Найдем с из ç 2 = a 2 + ᵬ 2 =144+25=169=13 2 . Поэтому Ƒ₁(-13,0), (-13) 2 /144-ʏ 2 /25=1, ʏ 2 =625/144, ʏ=25/12 расстояние от Ƒ₁ до точки пересечения перпендикуляра MF₁. МF₂ найдем из прямоугольного треугольника Ƒ₁MF₂: MF₂ 2 = MF₁ 2 + Ƒ₁F₂ 2 =(25/12) 2 +26 2 =(313/12) 2 . Следовательно, MF₂=313/12.

Пример 5. Определить точки M линии гипербола × 2 /9 - ʏ 2 /16 = 1, для которых MF₁ = 7.

Из условия задачи а = 3, ᵬ = 4 найдем с 2 = a 2 + b 2 = 9 + 16 = 25, c = 5. e = c/a =5/3, фокальный радиус для точек левой ветви r₁ = -e× - a =7 или -5/3*× - 3 = 7, 5× = -30, × = -6. y найдем из равенства 36/9 - y 2 /16 = 1, y 2 /16 = 3, y = ±√48=±4√3.

Пример 6. Составить уравнение гиперболы, если известны ее эксцентриситет e = 5/4, F(5,0), директриса 5× - 17 = 0.

Из условия задачи половина 1/2*F₁F₂ с = 5, e = 5/4 = c/a ⇒ a = 4. b 2 = с 2 - a 2 =5 2 - 4 2 =9. Ответ: × 2 /16-y 2 /9=1.

Переходим ко второй части статьи о линиях второго порядка, посвященной двум другим распространённым кривым – гиперболе и параболе. Если вы зашли на данную страницу с поисковика либо ещё не успели сориентироваться в теме, то рекомендую сначала изучить первый раздел урока, на котором мы рассмотрели не только основные теоретические моменты, но и познакомились с эллипсом. Остальным же читателям предлагаю существенно пополнить свои школьные знания о параболе и гиперболе. Гипербола и парабола – это просто? …Не дождётесь =)

Гипербола и её каноническое уравнение

Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.

У гиперболы две симметричные ветви.

У гиперболы две асимптоты.

Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас мы с неподдельным восхищением заглянем в декольте этой линии:

Построить гиперболу, заданную уравнением

Здесь можно сократить обе дроби, но оптимальнее сделать каждую из них трёхэтажной:

И только после этого провести сокращение:

Выделяем квадраты в знаменателях:

Почему преобразования лучше проводить именно так? Ведь дроби левой части можно сразу сократить и получить . Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае такой номер не проходит. Рассмотрим, например, уравнение . Здесь с делимостью всё печальнее и без трёхэтажных дробей уже не обойтись:

Итак, воспользуемся плодом наших трудов – каноническим уравнением :

Как построить гиперболу?

Существует два подхода к построению гиперболы – геометрический и алгебраический.
С практической точки зрения вычерчивание с помощью циркуля. я бы даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.

Целесообразно придерживаться следующего алгоритма, сначала готовый чертёж, потом комментарии:

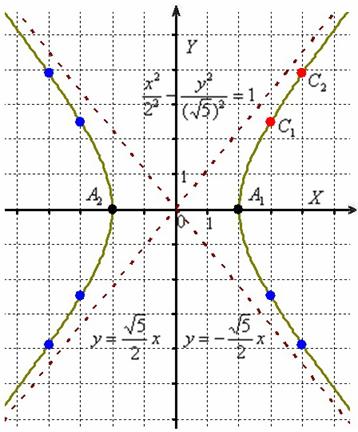
2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках . Выводится элементарно: если , то каноническое уравнение превращается в , откуда и следует, что . Рассматриваемая гипербола имеет вершины

3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения на черновике выражаем:

Уравнение распадается на две функции:
– определяет верхние дуги гиперболы (то, что нам надо);
– определяет нижние дуги гиперболы.

Напрашивается нахождение точек с абсциссами :

4) Изобразим на чертеже асимптоты , вершины , дополнительные и симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:

Техническая трудность может возникнуть с иррациональным угловым коэффициентом , но это вполне преодолимая проблема.

Отрезок называют действительной осью гиперболы,
его длину – расстоянием между вершинами;
число называют действительной полуосью гиперболы;
число – мнимой полуосью.

В нашем примере: , и, очевидно, если данную гиперболу повернуть вокруг центра симметрии и/или переместить, то эти значения не изменятся.

Определение гиперболы. Фокусы и эксцентриситет

У гиперболы, точно так же, как и у эллипса, есть две особенные точки , которые называются фокусами. Не говорил, но на всякий случай, вдруг кто неверно понимает: центр симметрии и точки фокуса, разумеется, не принадлежат кривым.

Общая концепция определения тоже похожа:

Гиперболой называют множество всех точек плоскости, абсолютное значение разности расстояний до каждой из которых от двух данных точек – есть величина постоянная, численно равная расстоянию между вершинами этой гиперболы: . При этом расстояние между фокусами превосходит длину действительной оси: .

Если гипербола задана каноническим уравнением , то расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: .
И, соответственно, фокусы имеют координаты .

Для исследуемой гиперболы :

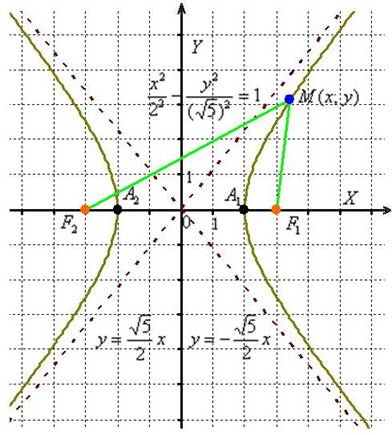
Разбираемся в определении. Обозначим через расстояния от фокусов до произвольной точки гиперболы:

Сначала мысленно передвигайте синюю точку по правой ветви гиперболы – где бы мы ни находились, модуль (абсолютное значение) разности между длинами отрезков будет одним и тем же:

Знак модуля нужен по той причине, что разность длин может быть как положительной, так и отрицательной. Кстати, для любой точки правой ветви (поскольку отрезок короче отрезка ). Для любой точки левой ветви ситуация ровно противоположная и .

Более того, ввиду очевидного свойства модуля безразлично, что из чего вычитать.

Удостоверимся, что в нашем примере модуль данной разности действительно равен расстоянию между вершинами. Мысленно поместите точку в правую вершину гиперболы . Тогда: , что и требовалось проверить.

Эксцентриситетом гиперболы называют отношение .

Для данного примера: .

По аналогии с эллипсом, зафиксировав значение , желающие могут провести самостоятельный анализ и проверку следующих фактов:

Равносторонняя гипербола

На практике часто встречается гипербола с равными полуосями. Если , то каноническое уравнение заметно упрощается:

А вместе с ним упрощаются и уравнения асимптот:

Так как , то , следовательно, эксцентриситет любой равносторонней гиперболы равен: .

Предлагаю закрепить теорию и практические навыки миниатюрной задачей:

Построить гиперболу и найти её фокусы.

Это пример для самостоятельного решения. Кто пропустит, тот пропустит многое ;-) Решение и чертёж в конце урока.

Начнём тревожить беззаботное существование нашей кривой:

Поворот вокруг центра и параллельный перенос гиперболы

Вернёмся к демонстрационной гиперболе . Что произойдёт, если в полученном уравнении поменять значения полуосей: ? Для эллипса данный трюк означал поворот на 90 градусов. Но здесь всё иначе! Уравнение определяет совершенно другую гиперболу. Ну, хотя бы обратите внимание на иные вершины: .

Теперь рассмотрим уравнение , которое очевидно тоже задаёт гиперболу. Однако к исходному уравнению оно также не имеет никакого отношения! Это предыдущая гипербола, повёрнутая на 90 градусов, с вершинами на оси ординат.

И, наконец, оставшийся случай задаёт нашу гиперболу , повернутую на 90 градусов. Как быть, если в практической задаче встретилась такая неканоническая запись?

Если требуется только построить кривую, то строим её в предложенном виде. Это довольно просто. Уравнения асимптот гиперболы обладают обратными угловыми коэффициентами:

И найдём несколько дополнительных точек:

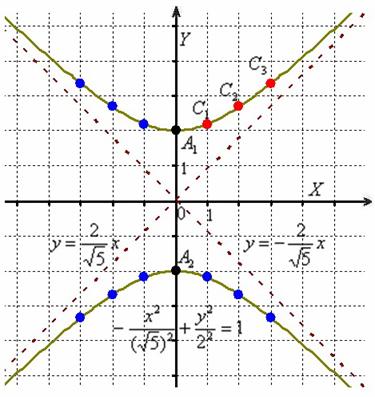
Выполним чертёж:

Помимо геометрии, похожие графики требуется строить в некоторых задачах математического анализа.

! Примечание: строгий теоретический подход предполагает поворот координатных осей, а не самой линии. При необходимости оформляйте решение по аналогии с соответствующим примечанием предыдущего урока.

Так, например, гипербола имеет центр симметрии в точке . Асимптоты, само собой, переместились вместе с гиперболой, их уравнения отыскиваются по формулам:

Полуоси и расстояние от фокусов до центра симметрии остались прежними, а вот координаты фокусов изменились с учётом параллельного переноса:

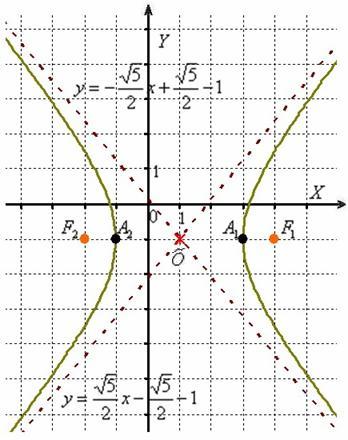
Параллельный перенос гиперболы доставил заметно больше хлопот, чем параллельный перенос эллипса, смотрим на картинку:

После таких трудов, уравнение трогать бессмысленно, но если таки просят, то придётся….

Или в строгом – с параллельным переносом системы координат началом в точку
(см. шаблон у эллипса).

На практике часто встречается комбинация поворота на произвольный угол и параллельного переноса гиперболы. Данная ситуация рассматривается на уроке Приведение уравнения линии 2-го порядка к каноническому виду.

Парабола и её каноническое уравнение

Решение: вершина известна, найдём дополнительные точки. Уравнение определяет верхнюю дугу параболы, уравнение – нижнюю дугу.

Для компактной записи результаты можно было свести в таблицу.

Перед тем, как выполнить элементарный поточечный чертёж, сформулируем строгое

определение параболы:

Параболой называется множество всех точек плоскости, равноудалённых от данной точки и данной прямой , не проходящей через точку .

Эксцентриситет любой параболы равен единице:

Поворот и параллельный перенос параболы

Парабола – одна из самых распространённых линий в математике, и строить её придётся действительно часто. Поэтому, пожалуйста, особенно внимательно отнестись к заключительному параграфу урока, где я разберу типовые варианты расположения данной кривой.

! Примечание: как и в случаях с предыдущими кривыми, корректнее говорить о повороте и параллельном переносе координатных осей, но автор ограничится упрощённым вариантом изложения, чтобы у читателя сложились элементарные представления о данных преобразованиях.

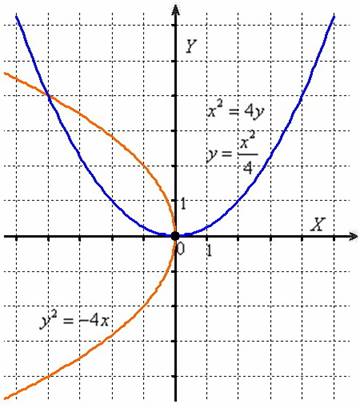
На следующем чертеже изображены графики кривых :

Оба уравнения задают неканоническое расположение нашей подопытной параболы , причём во втором случае легко получить функциональную запись, к которой мы привыкли в курсе математического анализа: .

Соответствующее творческое задание для самостоятельного решения:

Построить параболу . Привести уравнение линии к каноническому виду, найти фокус и уравнение директрисы.

Как лучше действовать?

По условию требуется построить параболу . Именно такую – в неканоническом виде! Поэтому в первой части задачи следует представить уравнение в виде , что позволит сразу определить вершину. Затем по образцу Примера 6 нужно провести поточечное построение линии, работая с уравнениями .

Вторая часть задания предполагает приведение уравнения к каноническому виду. Проанализируйте равенство – есть ли поворот, есть ли параллельный перенос? После того, как выясните каноническую запись , необходимо найти фокус параболы и уравнение её директрисы. Обратите внимание, что в контексте условия это, вероятнее всего, нужно сделать в каноническом положении!

Ну, а наша обзорная экскурсия подошла к концу, и я надеюсь, что у вас не возникло и не возникнет трудностей с тремя атлантами темы – эллипсом, гиперболой и параболой. Предлагаю узнать новый теоретический материал и закрепить практические навыки на уроке Задачи с линиями 2-го порядка.

Решения и чертежи:

И в общем случае – график обратной пропорциональности представляет собой равностороннюю гиперболу, уравнение которой можно привести к каноническому виду .

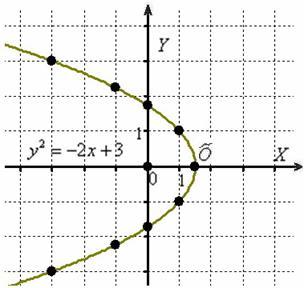
Пример 7: Решение: преобразуем уравнение:

Вершина параболы находится в точке , ветви направлены влево. С помощью уравнений найдём дополнительные точки:

Выполним чертёж:

Парабола получена путём поворота параболы на 180 градусов и её параллельного переноса в точку . Из канонического уравнения находим фокальный параметр , фокус и уравнение директрисы .
Примечание: в случае необходимости нетрудно найти координаты фокуса и уравнение директрисы неканонически расположенной параболы . Учитывая поворот и параллельный перенос: .

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

В геометрии большинство задач можно решить при помощи логических рассуждений. А там, где есть графики и кривые потребуется еще и скрупулезность. В этой статье рассмотрим часто встречающуюся кривую — гиперболу.

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие гиперболы

Каноническое уравнение гиперболы в алгебре выглядит так:

, где a и b — положительные действительные числа.

Кстати, канонический значит принятый за образец.

В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.

Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.

Вспомним особенности математической гиперболы:

• Две симметричные ветви.
• Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.

Если гипербола задана каноническим уравнением, то асимптоты можно найти так:

Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) - 4(y^2) = 20.

Приведем данное уравнение к каноническому виду (x^2)/(a^2) - (y^2)/(b^2) = 1.

Можно было сделать проще и дроби левой части 5(x^2)/20 - 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 - (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.

Если y = 0, то каноническое уравнение (x^2)/(a^2) - (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.

Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).

В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.

Способ такой же, как при построении эллипса. Из полученного канонического уравнения

на черновике выражаем:

Уравнение распадается на две функции:

— определяет верхние дуги гиперболы (то, что ищем);

— определяет нижние дуги гиперболы.

Далее найдем точки с абсциссами x = 3, x = 4:

Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.

Действительная ось гиперболы — отрезок А1А2.

Расстояние между вершинами — длина |A1A2| = 2a.

Действительная полуось гиперболы — число a = |OA1| = |OA2|.

Мнимая полуось гиперболы — число b.

В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.

Форма гиперболы

Повторим основные термины и узнаем, какие у гиперболы бывают формы.

Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.

Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.

Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.

Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.

Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.

Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Фокальное свойство гиперболы

Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).

Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .

Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:

Рассмотрим, как это выглядит на прямоугольной системе координат:

• пусть центр O гиперболы будет началом системы координат;
• прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
• прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:

Запишем это уравнение в координатной форме:

Избавимся от иррациональности и придем к каноническому уравнению гиперболы:

, т.е. выбранная система координат является канонической.

Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) - (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисы гиперболы — это две прямые, которые проходят параллельно оси.

ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.

Директориальное свойство гиперболы звучит так:

Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.

Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

На самом деле для фокуса F2 и директрисы d2 условие

можно записать в координатной форме так:

Избавляясь от иррациональности и заменяя e = a/c, c^2 - a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:

Построение гиперболы

Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.

Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.

В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:

Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:

Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.

По определению эксцентриситет гиперболы равен

Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.

Так как b^2 = c^2 - a^2, то величина b изменится.

При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.

Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 - y^2 = a^2

Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 - a^2 = a^2. И так как а и b положительные числа, получаем a = b.

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и есть величина постоянная , меньшая расстояния между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы .

Фокальное свойство гиперболы

Точки и называются фокусами гиперболы, расстояние между ними — фокусным расстоянием, середина — центром гиперболы, число и , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение , где , называется эксцентриситетом гиперболы . Из определения следует, что .

Геометрическое определение гиперболы , выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр к точке ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат оказалась правой).

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и . Для произвольной точки , принадлежащей гиперболе, имеем:

Записывая это уравнение в координатной форме, получаем:

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

где , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки директориальное свойство гиперболы ). Здесь

В самом деле, например, для фокуса и директрисы (рис.3.41,а) условие можно записать в координатной форме:

Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса и директрисы :

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид

В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке , принадлежащий прямой , но не содержащий точки (рис.3.41,б). Тогда для произвольной точки , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем . Выражаем расстояние между точками и (см. пункт 2 замечаний 2.8):

Следовательно, в координатной форме уравнение гиперболы имеет вид

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

Выражаем полярный радиус и делаем замены :

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы, для эллипса).

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения: . Следовательно, вершины имеют координаты . Длина отрезка, соединяющего вершины, равна . Длина отрезка оси ординат, соединяющего точки , равна . Этот отрезок называется мнимой осью гиперболы, а число Замечания 3.10.

1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы , описываемой уравнением (т.е. при ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка принадлежит гиперболе . то и точки и , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( при ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: . Учитывая, что и , получаем

Чем больше . Для равносторонней гиперболы имеем и . Для угол тупой, а для угол острый (рис.3.43,а).

6 . Две гиперболы, определяемые в одной и той же системе координат уравнениями и называются сопряженными друг с другом . Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение определяет гиперболу с центром в точке , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение определяет сопряженную гиперболу с центром в точке .

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

где — гиперболический косинус, a гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .

Пример 3.21. Изобразить гиперболу в канонической системе координат . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось, — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя

Следовательно, точки с координатами и принадлежат гиперболе. Вычисляем фокусное расстояние

эксцентриситет ; фокальныи параметр . Составляем уравнения асимптот , то есть , и уравнения директрис: .

В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.

Определение и функция гиперболы

Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

• x – независимая переменная;
• k ≠ 0;
• при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
• при k 0)
• y = -x (при k Алгоритм построения гиперболы

Пример 1

Дана функция y = 4 /_x. Построим ее график.

Решение

Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.

Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.

Читайте также:

  
• Русь накануне куликовской битвы кратко
  
• Альтернатива фашизму опыт великобритании и франции кратко
  
• Процентное отношение двух чисел 6 класс кратко
  
• Шарбель святой биография кратко
  
• Шаляпин биография кратко для детей