Геометрия вокруг нас 7 класс кратко

Обновлено: 05.07.2024

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Кое-кто, возможно, считает, что различные замысловатые линии, фигуры, поверхности можно встретить только в книгах учёных-математиков. Однако, стоит осмотреться, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Оказывается их очень много. Просто мы их не всегда замечаем.

Цель работы – исследовать какие геометрические фигуры, тела встречаются вокруг нас.

Исходя из поставленной цели, были поставлены следующие задачи:

- изучить использование геометрических форм и линий в практической деятельности человека;

- изучить некоторые природные творения в виде геометрических фигур;

- изучить использование геометрических фигур животными.

Методы исследования:

- изучение дополнительной литературы по данному вопросу

- наблюдение в повседневной жизни.

Геометрия у древних людей.

Треугольники, квадраты, ромбы, окружности… каждый ученик сталкивается с ними в школе на уроках геометрии.

Научная формулировка гласит, что геометрия – это раздел математики, который изучает пространственные фигуры и формы.

Ещё в эпоху неолита люди составляли на стенах пещер орнаменты из треугольников, ромбов, прямоугольников, кругов. Древние художники тонко чувствовали красоту геометрических форм; наскальные рисунки, выполненные с большой любовью к природе, радовали глаз. (рис.1) Человек отмечал равенство, симметрию, подобие фигур. Со временем он научился использовать свойства фигур в практической жизни. Геометрия – древнейшая наука, а первые геометры производили расчеты свыше тысячи лет назад.

Геометрические фигуры интересовали наших предков не только потому, что помогали решать практические задачи. Некоторые из фигур имели для людей магическое значение. Так, треугольник считался символом жизни, смерти и возрождения; квадрат – символом стабильности. Вселенную, бесконечность обозначали правильным пятиугольником – пентагоном, правильный шестиугольник – гексагон, являлся символом красоты и гармонии. Круг – знаком совершенства.

Геометрия в быту.

Стены, пол и потолок являются прямоугольниками (не будем обращать внимания на проёмы окон и дверей). Комнаты, кирпичи, шкаф, железобетонные блоки, напоминают своей формой прямоугольный параллелепипед. Посмотрим на паркетный пол. Планки паркета – прямоугольники или квадраты. Плитки пола в ванной, метро, на вокзалах чаще бывают правильными шестиугольниками или восьмиугольниками, между которыми уложены небольшие квадратики.

Многие вещи напоминают окружность – обруч, кольцо, дорожка вдоль арены цирка. Арена цирка, дно стакана или тарелки имеют форму круга. Фигура, близкая к кругу, получится, если разрезать поперек арбуз. Нальем в стакан воду. Её поверхность имеет форму круга. Если наклонить стакан, чтобы вода не выливалась, тогда край водной поверхности станет эллипсом. А у кого-то есть столы в виде круга, овала или очень плоского параллелепипеда.(рис. 2)

Ведро имеет форму усеченного конуса, у которого верхнее основание больше нижнего. Впрочем, ведро бывает и цилиндрической формы. Вообще, цилиндров и конусов в окружающем нас мире очень много: трубы парового отопления, кастрюли, бочки, стаканы, абажур, кружки, консервная банка, круглый карандаш, бревно и др. ( рис.2)

Геометрия в архитектуре.

Дом приблизительно имеет вид прямоугольного параллелепипеда. В современной архитектуре смело используются самые разные геометрические формы. Многие жилые дома, общественные здания украшаются колоннами. (рис 2а)

А как красив Московский Кремль. Прекрасны его башни! Сколько интересных геометрических фигур положено в их основу! Например, Набатная башня. На высоком параллелепипеде стоит параллелепипед поменьше, с проемами для окон, а ещё выше воздвигнута четырехугольная усечённая пирамида. На ней расположены четыре арки, увенчанные восьмиугольной пирамидой (см. рис.8). Геометрические фигуры различной формы можно узнать и в других замечательных сооружениях, возведенных русскими зодчими. (рис.7а – собор Василия Блаженного)

Выразительный контраст треугольника и прямоугольника на фасаде привлекает внимание посетителей музея Гронингена (Голландия) (рис.9) Круглая, прямоугольная, квадратная – все эти формы прекрасно уживаются в здании Музея современного искусства в Сан-Франциско (США) (см. рис.10). Здание Центра современного искусства имени Жоржа Помпиду в Париже – сочетание гигантского прозрачного параллелепипеда с ажурной металлической арматурой. (рис.11) Главные элементы здания больницы в Берлине (Германия) – прямоугольники и окружности ( рис.12). Геометрическая форма железнодорожной станции в аэропорту Лиона (Франция) напоминает древнюю гигантскую птицу и при этом сооружение суперсовременно (рис.13).

А сколько геометрических фигур можно найти в конструкциях мостов. На парапете моста часто укрепляют спасательные круги. Они по форме очень близки к тору.(см. рис.14)

4. Геометрия транспорта

По улице движутся автомобили, трамваи, троллейбусы. Их колеса с геометрической точки зрения – круги. В окружающем нас мире встречается много различных поверхностей, сложных по форме, не имеющих специальных названий.

Паровой котел напоминает цилиндр. В нем находится пар под высоким давлением. Поэтому стенки цилиндра слегка (незаметно для глаза) изгибаются, образуя поверхность очень сложной и неправильной формы, которую инженеры должны знать, чтобы суметь правильно рассчитать котел на прочность. Сложную форму имеет и корпус подводной лодки. Он должен быть хорошо обтекаемым, прочным и вместительным. От формы корабельного корпуса зависит и прочность корабля, и его устойчивость и скорость. Результат работы инженеров над формой современных автомобилей, поездов, самолетов - высокие скорости движения. Если форма будет удачной, обтекаемой, сопротивление воздуха значительно уменьшается, за счет чего увеличивается скорость. Сложную форму имеют и детали машин – гайки, винты, зубчатые колеса и т.д. (рис15,15а, 16)

Рассмотрим ракеты и космические корабли. Корпус ракеты состоит из цилиндра (в котором находятся двигатель и горючее), а в конической головной части помещается кабина с приборами или с космонавтом.

Комбинации окружающем нас мире.

Телевизионная башня, построенная замечательным русским советским инженером В.Г. Шуховым. Она состоит из частей, которые математики называют гиперболоидами вращения. Хотя сами части кривые, они сложены из прямолинейных металлических балок. Этим Шухов облегчил возведение башни (рис.17, 17а –Эйфелева башня).

Колонны в большинстве случаев – цилиндры, но могут иметь и более сложную форму. А обелиски в память погибших – четырехгранные столбы, сужающиеся к верху.

6. Природные творения в виде геометрических фигур.

До сих пор рассматривали некоторые геометрические формы, созданные руками человека. Но ведь в самой природе очень много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой.

Кристалл соли имеет форму куба. (рис.19а) Кристаллы горного хрусталя напоминают отточенный с двух сторон карандаш. Алмазы чаще всего встречаются в виде октаэдра, иногда куба (см. рис 19). Существуют и многие микроскопические многоугольники. В микроскоп можно увидеть, что молекулы воды при замерзании располагаются в вершинах и центрах тетраэдров. Атом углерода всегда соединен с четырьмя другими атомами тоже в форме тетраэдра. Одна из самых изысканных геометрических фигур падает на нас с неба в виде снежинок.

Обычная горошина имеет форму шара. И это неспроста. Когда стручок гороха созреет и лопнет, горошины упадут на землю и благодаря своей форме покатятся во все стороны, захватывая всё новые территории. Горошины кубической или пирамидальной формы так и остались бы лежать возле стебля. Шаровую форму принимают капельки росы, капли ртути из разбитого градусника, капли масла, оказавшиеся в толще воды… Все жидкости в состоянии невесомости обретают форму шара. Отчего шар так популярен? Это объясняется одним замечательным свойством: на изготовление шара расходуется значительно меньше материала, чем на сосуд любой другой формы того объёма. Поэтому, если вам нужен вместительный мешок, а ткани не хватает, шейте его в форме шара. Шар – единственное геометрическое тело, у которого наибольший объём заключен в наименьшую оболочку.

7. Использование геометрических форм животными.

Животные, конечно, же геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел.

Многие птицы – воробьи, крапивники, лирохвосты – строят свои гнёзда в форме полушара (см. рис.20).

Есть архитекторы и среди рыб: в пресных водах живет удивительная рыба колюшка. В отличие от многих своих соплеменников она живет в гнезде, которое имеет форму шара (см. рис. 21). Но самые искусные геометры – пчёлы. Они строят соты из шестиугольников. Любая ячейка в сотах окружена шестью другими ячейками. А основание, или донышко, ячейки представляет собой трехгранную пирамиду. Такая форма выбрана неспроста. В правильный шестиугольник поместится больше меда, а зазоры между ячейками будут наименьшими! Разумная экономия усилий и строительных материалов (см. рис.22).

Исследовательская работа ученика 7 класса по теме: "Геометрия вокруг нас". Цель данной работы: показать практическое применение геометрии.

Вложение	Размер
tvorcheskaya_rabota_geometriya_vokrug_nas.docx	42.26 КБ

Предварительный просмотр:

Муниципальное автономное образовательное учреждение

Автор: Зырянов Кирилл, 7 класс

Научный руководитель: Пахомова

2.2 Геометрия в жизни людей…….…………………………………….6

2.3. Геометрия в природе………………………………………………. 7

2.4. Практическое применение геометрии …..…………………………8

Заключение………………………………………………………..…. 11
Список использованных источников, литературы…………………12

«Геометрия является самым могущественным средством

для изощрения наших умственных способностей и дает

Проблема исследования: как можно применить на практике знания, полученные на уроках геометрии, есть ли связь между геометрией и другими учебными предметами.

Объект исследования: геометрия.

Предмет исследования: практическое применение геометрии.

Гипотеза исследования: геометрия необходима не только как школьная дисциплина, но и важна в повседневной жизни.

Цель исследования: Роль геометрии в жизни человека.

Исследовать и показать как можно больше способов практического применения геометрии.
Научиться их применять в повседневной жизни.
Показать одноклассникам практическое применение геометрии.

- поисковый метод с использованием научной и учебной литературы, интернета;

- исследовательский метод при решении практических задач по геометрии.

II. Основная часть.

2.1. Немного истории.

2.2. Геометрия в жизни человека.

Геометрические знания связаны со многими современными специальностями. Например, архитектор, который перед тем как построить жилое здание, придумывает основную концепцию здания, его облик, проектируют будущую постройку на чертежах в уменьшенном масштабе. Задача архитектора — спроектировать сооружение, максимально отвечающее потребностям заказчика.

Оказывается геометрия тесно связана с искусством, т.к. одним из ранних этапов развития искусства Древней Греции (IX-VIII вв. до н. э.) является техника геометрической живописи. Это проявляется в росписи утвари. Геометрическому стилю присуще многообразие и четкость узоров , их строгость подчёркивает построение конструктивного предмета . Орнамент располагается полосами и получается из ломанных линий, крестов, окружностей. В более поздний период развития Древней Греции появляется изображение образа человека из геометрических фигур. А в начале XX века появилось авангардное направление в живописи –кубизм . В этом направлении используется множество геометрических фигур.

Геометрия непосредственно связана с модой. Множество геометрических фигур можно увидеть в основных частях костюма. Построение геометрических фигур необходимо не только на уроках геометрии, но и в конструировании одежды.

Самым неожиданным для меня явилось то, что геометрия нужна в психологии. В психологии есть система, с помощью которой можно определить характер человека, его способности, манеру общения. Данная система называется- психогеометрия. В основе психогеометрии лежит пять типов личности, которым соответствуют геометрические фигуры квадрат , треугольник , прямоугольник , круг и загзаг . Человек выбирает ту, с которой ассоциируете себя. Оставшиеся фигуры пронумерует в порядке убывания предпочтения. Выбранная фигура и определяет основные черты характера. А последняя фигура, в вашем пронумерованном списке, может обозначать персоны, контакты с которой будут наиболее затруднительными для тестируемого.

2.3 Геометрия в природе.

Если посмотреть вокруг, то можно увидеть что большая часть тел в природе имеют шарообразную форму. Примером могут служить ягоды, фрукты, цветы и даже некоторые животные имеют форму шара. Например, рыба-еж, ядовитая рыба – фугу. Икра всех рыб представляет форму шара. Многие бактерии - шарообразны. Если взять любое насекомое, то его как будто сконструировали по чертежу. Глаза стрекозы, занимающие большую часть её головы, состоят из более 30 000 мелких глазков (фасеток). Что интересно, каждый миниатюрный глаз способен работать независимо от других. Верхняя часть фасеток предназначена для распознавания формы предмета, а нижняя – его цвета. Яйца у птиц имеют шаровидную или продолговатую форму. Многие животные спят, свернувшись клубком, т.к. поверхность тела уменьшается, и тепло лучше сохраняется. Итак, природа часто использует круг и его объемный эквивалент – сферу. Небесные тела большой массы, такие как звезды, планеты и спутники тоже сферической формы. Сила притяжения толкает каждый атом к центру тела. Со временем оно приобретает сферическую форму, потому что именно в ней достигается максимальная концентрация массы при минимальной площади внешней поверхности.

Конечно не только шарообразная форма присутствует в природе. Например, пчелы строят соты в форме шестиугольников, что позволяет им хранить максимально возможное количество меда, используя минимальное количество воска.

Есть около 5000 типов пауков, и все они создают почти идеальное круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.

Один из примеров симметрии являются круги на полях, которые отличаются сложностью дизайна и невероятной симметрией, даже после того, как создатели кругов признались и продемонстрировали свое мастерство, многие люди до сих пор верят, что это сделали космические пришельцы.

Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.

2.4 Практическое применение геометрии.

Сделав вывод о том ,что природа всегда останавливает выбор на самых стабильных формах, минимально расходующих энергию, я подумал о том, чем мне может помочь геометрия в жизни. Не зря ли я трачу время на изучение данного предмета? Возможно они мне пригодятся только для того, чтобы измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Перед нами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше?

Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d 2 ).

Задача №2. Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам?

Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна . Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно.

Задача№3. Прямоугольная калитка со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать.

Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

Задача №4. На какой табурет можно сесть без риска оказаться на полу, на тот у которого ножки и сиденье образуют треугольник или квадрат?

Решение. Безопасный табурет тот, у которого сиденье и ножки образуют треугольник(более устойчив).

Задача №6. Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня?

Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести.

Задача №7. Один из вопросов, который меня всегда мучил – почему крышки люков круглые?

Оказывается есть еще ответ, который опирается на знания формул площадей круга и квадрата. Люки делают круглыми с целью снижения себестоимости их производства. Это обусловливается спецификой оборудования: для того, чтобы изготовить круглую крышку, необходимо меньше материала. Стандартные нормы ширины люка – 600 мм, для круга это будет диаметр, а для квадрата – сторона, поэтому площадь квадратного люка будет равна 0,36 квадратных метров, а круглого – на 30 % меньше.

Еще одна практическая сторона: крышка люка круглая, поскольку ее удобно переносить. В большинстве случаев крышки люков делают из рашпера (серого чугуна), который получают путем переплавки различного металлолома. Вес одной крышки варьирует от 50 до 110 кг. Одному человеку перенести крышку люка с одного места на другое довольно тяжело, а благодаря круглой форме его можно перекатить.

Не квадратные, а именно люки круглой формы удобно монтировать и демонтировать, поскольку точки концентрации нагрузки идут по всей окружности крышки, в то время как у люков квадратной или прямоугольной формы такими точками будут только углы. Именно поэтому горлышки и, соответственно, крышки к банкам изготавливают круглыми.

Выдвинутая гипотеза о том, что геометрия необходима не только как школьная дисциплина, но и важна в повседневной жизни – подтвердилась.

Краткий курс геометрии 7 класс

☑ 1. Простейшие геометрические фигуры и их свойства

Аксиома. Основное свойство прямой: Через любые две точки можно провести прямую, и притом только одну.
Определение. Пересекающиеся прямые: Две прямые, имеющие общую точку, называют пересекающимися.
ТЕОРЕМА. О двух пересекающихся прямых: Любые две пересекающиеся прямые имеют только одну общую точку.
Два отрезка называют равными, если их можно совместить наложением.
Аксиома. Основное свойство длины отрезка: Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и т. е. АВ = АС + СВ.
Расстоянием между точками называют длину отрезка АВ.
Два луча, имеющие общее начало и лежащие на одной прямой, называют дополнительными.

☑ 2. Углы

Углом называется геометрическая фигура (рис. 1), образованная двумя лучами, исходящими из одной точки.
Точка О — вершина угла, а лучи ОА и ОБ — стороны угла. Обозначение: ∠AOB или ∠ab.
Угол в 90° называется прямым (рис. 2).
Угол, меньший прямого, называется острым (рис. 3).
Угол, больший прямого, но меньший развернутого, называется тупым (рис. 4).

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого (рис. 5).
∠AOC и ∠DOB; ∠BOC и ∠AOD — вертикальные.
Вертикальные углы равны: ∠AOC = ∠DOB и ∠BOC = ∠AOD.
Два угла называются смежными, если у них одна сторона общая, а две другие составляют прямую линию (рис. 6), ∠AOC и ∠BOC — смежные.

Сумма смежных углов равна 180°.
Биссектрисой угла называется луч, проходящий между сторонами угла и делящий его пополам (рис. 7).
Биссектрисы вертикальных углов составляют продолжение друг друга (рис. 8).
Биссектрисы смежных углов взаимно перпендикулярны (рис. 9).

При пересечении двух прямых a и b третьей с (секущей) образуется 8 углов (рис. 10):

соответственные углы: ∠1 и ∠5, ∠2 и ∠6, ∠4 и ∠8, ∠3 и ∠7;
внутренние накрест лежащие: ∠4 и ∠6, ∠3 и ∠5;
внешние накрест лежащие: ∠1 и ∠7, ∠2 и ∠8;
внутренние односторонние: ∠4 и ∠5, ∠3 и ∠6;
внешние односторонние: ∠1 и ∠8, ∠2 и ∠7.

☑ 3. Параллельные прямые

Две прямые называют параллельными, если они не пересекаются.
Аксиома параллельности прямых: Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Признаки параллельности двух прямых:
• Две прямые, перпендикулярные третьей прямой, параллельны.
• Если накрест лежащие углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
• Если сумма односторонних углов, образующихся при пересечении двух прямых секущей, равна 180°, то прямые параллельны.
• Если соответственные углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
Свойства параллельных прямых:
• Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.
• Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.
• Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180°.
Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

☑ 4. Треугольник

Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, последовательно соединяющих эти точки.
Точки А, В, С — вершины треугольника АВС.
Отрезки АВ, ВС и АС — стороны, ∠A, ∠B и ∠C — углы. ∠A + ∠B + ∠C = 180°.
Стороны треугольника часто обозначают малыми буквами (рис. 13): АВ = с, ВС = а, АС = b.
Р = а + b + с — периметр треугольника.

Треугольник, у которого все углы острые, называется остроугольным (см. рис. 13).
Треугольник, у которого есть прямой угол, называется прямоугольным (рис. 14).
Стороны, образующие прямой угол, называются катетами (а и b), а сторона, лежащая против прямого угла, — гипотенузой (с).
Треугольник с тупым углом называется тупоугольным (рис. 15).

Треугольник, у которого две стороны равны, называется равнобедренным (рис. 16).
Равные стороны называются боковыми, а третья сторона — основанием равнобедренного треугольника.
Треугольник, у которого все стороны равны, называется равносторонним (рис. 17).
Каждый угол равностороннего треугольника равен 60°.
Свойства равнобедренного треугольника:
1. Углы при основании равны.
2. Биссектриса, проведенная к основанию, является одновременно медианой и высотой.
3. Высота, проведенная к основанию, является одновременно медианой и биссектрисой.
4. Медиана, проведенная к основанию, является одновременно высотой и биссектрисой.

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника (рис. 18). ∠CBD — внешний угол треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним (см. рис. 18): ∠CBD = ∠A + ∠C.
Отрезок, соединяющий середины двух сторон, называется средней линией треугольника (рис. 19).

☑ 5. Признаки равенства треугольников

I признак (признак равенства по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 20). АВ = А₁В₁, АС = А₁С₁, ∠A = ∠A₁

II признак (признак равенства по стороне и прилежащим к ней углам).
Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 21). АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁

III признак (признак равенства по трем сторонам).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 22). АВ = А₁В₁, ВС = B₁C₁, АС =А₁С₁.

Вы смотрите:
Краткий курс геометрии 7 класс

☑ 6. Соотношения между сторонами и углами треугольника

ТЕОРЕМА о сумме углов треугольника. Сумма углов треугольника равна 180°. ∠A + ∠B + ∠C = 180°.
ТЕОРЕМА о соотношениях между сторонами и углами треугольника. В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.
Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.
Следствие 2. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
ТЕОРЕМА о неравенстве треугольника. Каждая сторона треугольника меньше суммы двух других сторон: а ☑ 7. Определение вида треугольника по его сторонам

Пусть с — наибольшая сторона, тогда:
а) если с 2 2 + b 2 , то треугольник остроугольный;
б) если с 2 > а 2 + b 2 , то треугольник тупоугольный;
в) если с 2 = а 2 + b 2 , то треугольник прямоугольный.

☑ 8. Прямоугольные треугольники (некоторые свойства)

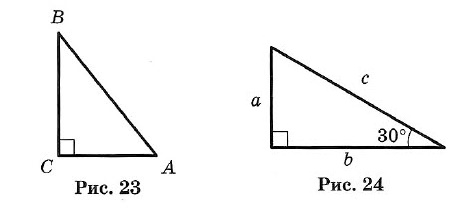
1. Сумма острых углов равна 90° (рис. 23). ∠A + ∠B = 90°.
2. Катет, лежащий против угла в 30°, равен половине гипотенузы (рис. 24). a = c/2
3. Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° (рис. 24).

☑ 9. Признаки равенства прямоугольных треугольников

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис. 25). АС = А₁С₁, ВС = В₁С₁.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны (рис. 26). АС = А₁С₁, ∠A = ∠A₁.

3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны (рис. 27). АВ = А₁В₁, ∠A = ∠A₁.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис. 28). АВ = А₁В₁, АС = А₁С₁

Краткий курс геометрии 7 класс

☑ 10. Четыре замечательные точки треугольника

С каждым треугольником связаны 4 точки:
1) точка пересечения медиан;
2) точка пересечения биссектрис;
3) точка пересечения высот (или их продолжений);
4) точка пересечения серединных перпендикуляров к сторонам.
Эти четыре точки называются замечательными точками треугольника.
Высотой треугольника называется длина перпендикуляра, опущенного из любой его вершины на противолежащую сторону или ее продолжение.

В тупоугольном треугольнике (рис. 29) две высоты падают на продолжение сторон и лежат вне треугольника, а третья внутри.
В остроугольном треугольнике (рис. 30) все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты одновременно служат и высотами (рис. 31).
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном треугольнике он совпадает с вершиной прямого угла.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Три медианы треугольника пересекаются в одной точке, которая является центром тяжести треугольника (рис. 32).
Эта точка делит каждую медиану в отношении 2 : 1 (считая от соответствующей вершины).
Биссектрисой треугольника называется отрезок биссектрисы угла от вершины до пересечения с противолежащей стороной.
Три биссектрисы треугольника пересекаются в одной точке, которая является центром вписанного круга (рис. 33).
Три перпендикуляра к сторонам треугольника, проведенные через их середины (рис. 34, 35, 36), пересекаются в одной точке, которая является центром описанной окружности.

В тупоугольном треугольнике (рис. 34) эта точка лежит вне треугольника, в остроугольном (рис. 35) — внутри, в прямоугольном — на середине гипотенузы (рис. 36).
Ортоцентр, центр тяжести, центр вписанной и описанной окружностей совпадают друг с другом только в равностороннем треугольнике.

☑ 11. Окружность

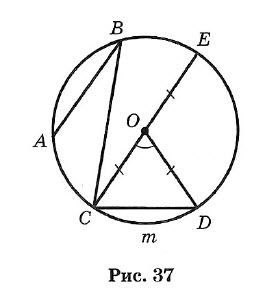
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R. На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр. Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

☑ 12. Свойства касательных к окружности

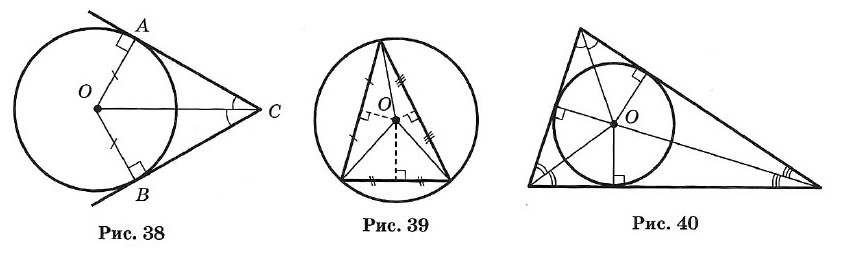
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.

☑ 13. Окружность и треугольник

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

Вятский колледж культуры

Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике, свести параллели к схождению и раздвинуть перпендикуляры к прямой на расхождение.

Люди испокон веков привыкли к тому, что разнообразие геометрических фигур (линий, кругов, многогранников и т.д.) можно встретить лишь в учебниках геометрии, компьютерной графике или даже в специальной литературе. Но это не так. Многообразие геометрических примеров можно встретить и в повседневной жизни. Например, кухонный шкаф, круглое зеркало, египетская пирамида, лист бумаги и т.д.

Многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Просто мы их не всегда замечаем.

Научная формулировка гласит, что геометрия – это раздел математики, который изучает пространственные фигуры и формы. Так ли это? И когда геометрия появилась в жизни людей на самом деле?

Ещё в эпоху палеолита доисторические люди изготовляли орудие из кремня. При помощи округлого камня, используя его в качестве молотка, придавали орудию форму треугольника. Отколоть кусочек кремня сравнительно просто, но придать ему нужную форму – вот нелёгкая задача. Идея симметрии знаменует большой шаг вперёд и является началом понятия пропорциональности, иными словами, ощущения того, что, если придать орудию форму, оно будет не только таким же острым, как необработанный кремень, но и более приятным на вид и удобным в обращении.

Практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д.

Это не может не поражать и не удивлять человеческий разум. За прошедшие тысячелетия и даже столетия было задумано и построено множество шедевров архитектуры, но даже те из них, которые были намного моложе египетских пирамид, давно канули в вечность; пирамиды же, хотя и частично разрушенные, стоят до сих пор, и простоят ещё очень долго.

Можно привести ещё много различных примеров архитектурных особенностей окружающих человека испокон веков. Некоторые из них сделала сама природа. Особенности их происхождения до сих не известны человеку и поражают их воображение.

Это лишний раз доказывает, что геометрия в жизни людей появилась вместе с развитием мышления человека.

В наши дни архитектура имеет всё более разнообразный характер. Здания разных форм и размеров. Многие из них украшаются колоннами, арками, лепнинами, столбами и другими удивительными элементами.

Так же, как и в древности современные архитекторы ломают все стереотипы об архитектуре. Например, Храм Лотоса (Дели, Индия), это огромное здание из белоснежного пентелийского мрамора в форме распускающегося цветка лотоса – одна из наиболее популярных среди туристов достопримечательностей Дели. Известен как главный храм Индийского субконтинента и главная достопримечательность города. Удивительное сооружение не имеет в своей конструкции ни единой прямой линии, только плавные изгибы! А в его естественной вентиляционной системе воплощены принципы, использовавшиеся при строительстве древних храмов. Холодный воздух поступает снизу, проходя через систему бассейнов и фундамент, нагревается внутри здания и выходит через отверстие в куполе. Температура внутри храма благодаря этому всегда вполне комфортная, хотя и прохладная.

Чаще всего именно в быту можно увидеть геометрические фигуры. В каждой квартире встречается что-то квадратное, круглое, овальное, цилиндрическое, прямоугольное и так далее. Обручальное кольцо, зеркало, тарелки, кружки, цветочный горшок имеют форму круга или овала. Микроволновая печь, кирпичи, шкаф, железобетонные блоки, напоминают своей формой прямоугольный параллелепипед. В ремонте так же используются геометрические особенности. Например, для того, чтобы купить обои, нужно знать и рассчитать площадь стен комнаты. Это помогает избежать переплаты за не нужные рулоны, которые так и не понадобятся.

Уже можно понять, что руками человека создано не мало геометрических конструкций, но и природа не уступает. Если вы когда-нибудь наблюдали за снежинками, то замечали, что у них разные формы. Считается, что в одном кубическом метре снега находится около 350 млн. снежинок! Все они шестиугольные и имеют кристаллоподобные структуры, но у каждой своя уникальная форма. В Германии немецкий математик и астроном Йоган Кеплер обратил внимание на шестерную симметрию снежинок. Он попытался объяснить её тем, что кристаллы построены из мельчайших одинаковых шариков, теснейшим образом присоединенных друг к другу.

На уроках биологии рассматривая в микроскоп кусочек лука можно было увидеть, как клетки соединены между собой, и как напоминают форму прямоугольника. Атом углерода всегда соединен с четырьмя другими атомами тоже в форме тетраэдра.

Горошина имеет форму шара не просто так. Когда стручок гороха созреет и лопнет, горошины упадут на землю и благодаря своей форме покатятся во все стороны, захватывая всё новые территории. Горошины кубической или пирамидальной формы так и остались бы лежать возле стебля. Шаровую форму принимают капельки росы, капли ртути из разбитого градусника, капли масла, оказавшиеся в толще воды…

Таким образом, геометрия в нашей жизни встречается абсолютно везде и во всём, играет не малую роль, и до сих пор открывает для нас новые перспективы. Она является неотъемлемой частью жизни всего на земле. Ежедневно множество разнообразных геометрических линий и поверхностей использует человек в своей деятельности, и пользуясь геометрическими данными и вычислениями, с наибольшей точностью решает разнообразные технические задачи.

Список использованных источников

2. М. Квеннелл, Ч. Квеннелл Первобытные люди. Быт, религия, культура – Центрполиграф, 2005.

3. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев Геометрия: Учебник. 10-11 класс – Москва: Просвещение, 2013.

Читайте также: