Геометрия 10 класс теория кратко
Обновлено: 05.07.2024
Материалы к зачетной работе по теме
"Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей"
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
Аксиомы стереометрии и их следствия
Аксиома 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
Некоторые следствия из аксиом
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема о трех прямых в пространстве.
Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Теорема.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Взаимное расположение прямых в пространстве
Пересекающиеся прямые:
лежат в одной плоскости, имеют одну общую точку.
Параллельные прямые:
лежат в одной плоскости, не имеют общих точек (не пересекаются)
Скрещивающиеся прямые:
не лежат в одной плоскости, не имеют общих точек (не пересекаются)
Параллельность плоскостей
Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β.
Признак параллельности двух плоскостей
Теорема.
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны.
Если а∥а1 и b∥b1, то α∥β.
Свойства параллельных плоскостей
Вели α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
1.1 Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
1.2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
1.3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
2. Некоторые следствия из аксиом.
2.1 Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
2.2 Через две пересекающиеся прямые проходит плоскость, и притом только одна.
3. Параллельность прямых, прямой и плоскости.
3.1 Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
3.2 Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
3.3 Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
3.4 Если две прямые параллельны третьей прямой, то они параллельны.
3.5 Прямая и плоскость называются параллельными, если они не имеют общих точек.
3.6 Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
4. Взаимное расположение прямых в пространстве. Угол между двумя прямыми.
4.1 Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
4.2 Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся
4.3 Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой, и притом только одна.
4.4 Если стороны двух углов соответственно сонаправлены, то такие углы равны.
5. Параллельность плоскостей.
5.1 Две плоскости называются параллельными, если они не пересекаются.
5.2 Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
6. Перпендикулярность прямой и плоскости.
6.1 Если одна из двух параллелельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
6.2 Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
6.3 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
6.4 Если две прямые перпендикулярны к плоскости, то они параллельны.
6.5 Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
6.6 Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
7. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
7.1 Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
7.2 Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекции на плоскость.
8. Двугранный угол. Перпендикулярность плоскостей.
8.1 Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
8.2 Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90 0 .
8.3 Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
8.4 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его трёх измерений.
8.5 Сумма плоских углов многогранного угла меньше 360 0 .
9. Теорема Эйлера.
В любом выпуклом многограннике сумма числа граней и вершин больше числа рёбер на 2.
10. Призма
10.1 Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
11. Пространственная теорема Пифагора.
Если все плоские углы при одной из вершин тетраэдра – прямые, то квадрат площади грани, противолежащей этой вершине, равен сумме квадратов площади остальных граней.
12. Пирамида
12.1 Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
12.2 Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
13. Вектор
13.1 Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.

13.2 Для любых трёх точек A, B и C имеет место равенство
13.5 Произведением ненулевого вектора на число k называется такой вектор длина которого равна причём векторы и сонаправлены при k>0 и противоположно направлены при k Нравится Загрузка.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Если прямая , не лежащая в плоскости , параллельна какой-нибудь прямой , лежащей в этой плоскости , то она параллельна данной плоскости .
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и при том только одна.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
по математике (геометрия)
Геометрия изучает пространственные свойства предметов, оставляя в стороне все остальные их признаки. Например, резиновый мяч диаметром 25 см и чугунное ядро того же диаметра отличаются друг от друга по весу, по цвету, по твердости и т. д. Однако все эти признаки мяча и ядра в геометрии оставляются без внимания; пространственные же их свойства (форма и размеры) одинаковы. С точки зрения геометрии каждый из этих предметов представляет шар диаметром 25 см.
Предмет, от которого мысленно отняты все его свойства, кроме пространственных, называется геометрическим телом . Шар есть одно из геометрических тел.
Идя дальше по пути отвлечения, мы получаем, понятия геометрической поверхности , геометрической линии и геометрической точки . Поверхность мы мысленно отделяем от тела, которому она принадлежит, и лишаем ее толщины. Линию мы лишаем толщины и ширины, а точку вовсе лишаем измерений. Мы мыслим, что точка может служить границей линии (или ее части), линия — границей поверхности и поверхность — границей тела. Мы мыслим также, что точка может двигаться и своим движением порождать линию, линия может движением порождать поверхность, а поверхность — порождать тело.
В природе нет точек, лишенных измерений, но есть предметы столь малых размеров, что их в некоторых условиях можно принять за геометрические точки. В природе нет также ни геометрических, линий, ни геометрических поверхностей, но все свойства линий и поверхностей, найденные в геометрии, находят многообразные применения в науке и технике. Это происходит потому, что геометрические понятия порождены пространственными свойствами действительного мира. Отвлеченная форма геометрических понятий для того и служит, чтобы эти свойства изучать в чистом их виде.
Первые геометрические понятия приобретены людьми в глубокой древности. Они возникли из потребности определять вместимость различных предметов (сосудов, амбаров и т. п.) и площади земельных участков. Древнейшие известные нам письменные памятники, содержащие правила для определения площадей и объемов, были составлены в Египте и Вавилоне около 4 тысяч лет назад. Около 2 1 / 2 тысяч лет назад греки заимствовали у египтян и вавилонян их геометрические знания. Первоначально эти знания применялись преимущественно для измерения земельных участков. Отсюда и греческое название "геометрия", что означает "землемерие".
Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.
Эта система около 300 г. до н. э. получила завершенный вида "Началах" Евклида, где изложены также основы теоретической арифметики. Геометрические разделы "Начал" по содержанию и по строгости изложения примерно совпадают с нынешними школьными учебниками геометрии.
Однако там ничего не говорится ни об объеме, ни о поверхности шара, ни об отношении окружности к диаметру (хотя есть теорема о том, что площади кругов относятся, как квадраты диаметров). Приближенная величина этого отношения была известна из опыта задолго до Евклида, но только в середине 3 века до н. э. Архимед (287 — 212 гг.) строго доказал, что отношение окружности к диаметру (т. е., по-нашему, число ) заключено между 3 1 / 7 и 3 10 / 70 . Архимед доказал также, что объем шара меньше объема описанного цилиндра ровно в 1 1 / 2 раза и что поверхность шара в 1 1 / 2 раза меньше полной поверхности описанного цилиндра.
В способах, примененных Архимедом для решения упомянутых задач, содержатся зачатки методов высшей математики. Эти способы Архимед применил к решению многих трудных задач геометрии и механики, очень важных для строительного дела и для мореплавания. В частности, он определил объемы и центры тяжести многих тел и изучил вопрос о равновесии плавающих тел различной формы.
Греческие геометры исследовали свойства многих линий, важных для практики и для теории. Особенно полно они изучили конические сечения . Во втором веке до н. э. Аполлоний обогатил теорию конических сечений многими важными открытиями, остававшимися непревзойденными в течение 18 веков.
Для изучения конических сечений Аполлоний пользовался методом координат . К изучению всевозможных линий на плоскости этот метод был применен лишь в 30-х годах 17 века французскими учеными Ферма (1601—1655) и Декартом (1596—1650). Для технической практики того времени было достаточно плоских линий. Лишь сто лет спустя, когда этого потребовали возросшие запросы астрономии, геодезии и механики, координатный метод был применен к изучению кривых поверхностей и линий, проведенных на кривых поверхностях.
Более двух тысяч лет система Евклида считалась непреложной. Но в 1826 г. гениальный русский ученый Николай Иванович Лобачевский создал новую геометрическую систему. Исходные ее положения отличаются от основных положений, Евклида лишь в одном пункте (В геометрии Эвклида через точку А проходит только одна прямая, лежащая в одной плоскости с данной прямой BC и не пересекающая её. В геометрии Лобачевского таких прямых бесчисленное множество). Но отсюда вытекает множество очень существенных особенностей.
Так, в геометрии Лобачевского сумма углов треугольника всегда меньше, чем 180° (в геометрии Евклида она равна 180°). При этом недостаток до 180° тем больше, чем больше площадь треугольника.
Может показаться, что опыт опровергает этот и другие выводы Лобачевского. Но это не так. Непосредственно измеряя углы треугольника, мы находим, что они в сумме составляют примерно 180°. Точной же величины суммы мы не можем найти вследствие несовершенства измерительных инструментов. Между тем все те треугольники, которые доступны нашему измерению, слишком малы, чтобы непосредственными измерениями обнаружить недостаток суммы углов до 180°.
При дальнейшем развитии гениальных идей Лобачевского оказалось, что система Евклида недостаточна для исследования многих вопросов астрономии и физики, где мы имеем дело с фигурами огромных размеров. Однако в условиях обычного опыта она остается вполне пригодной. А так как к тому же она обладает преимуществом простоты, то её применяют и будут применять в технических расчетах, её изучают и будут изучать в школах.
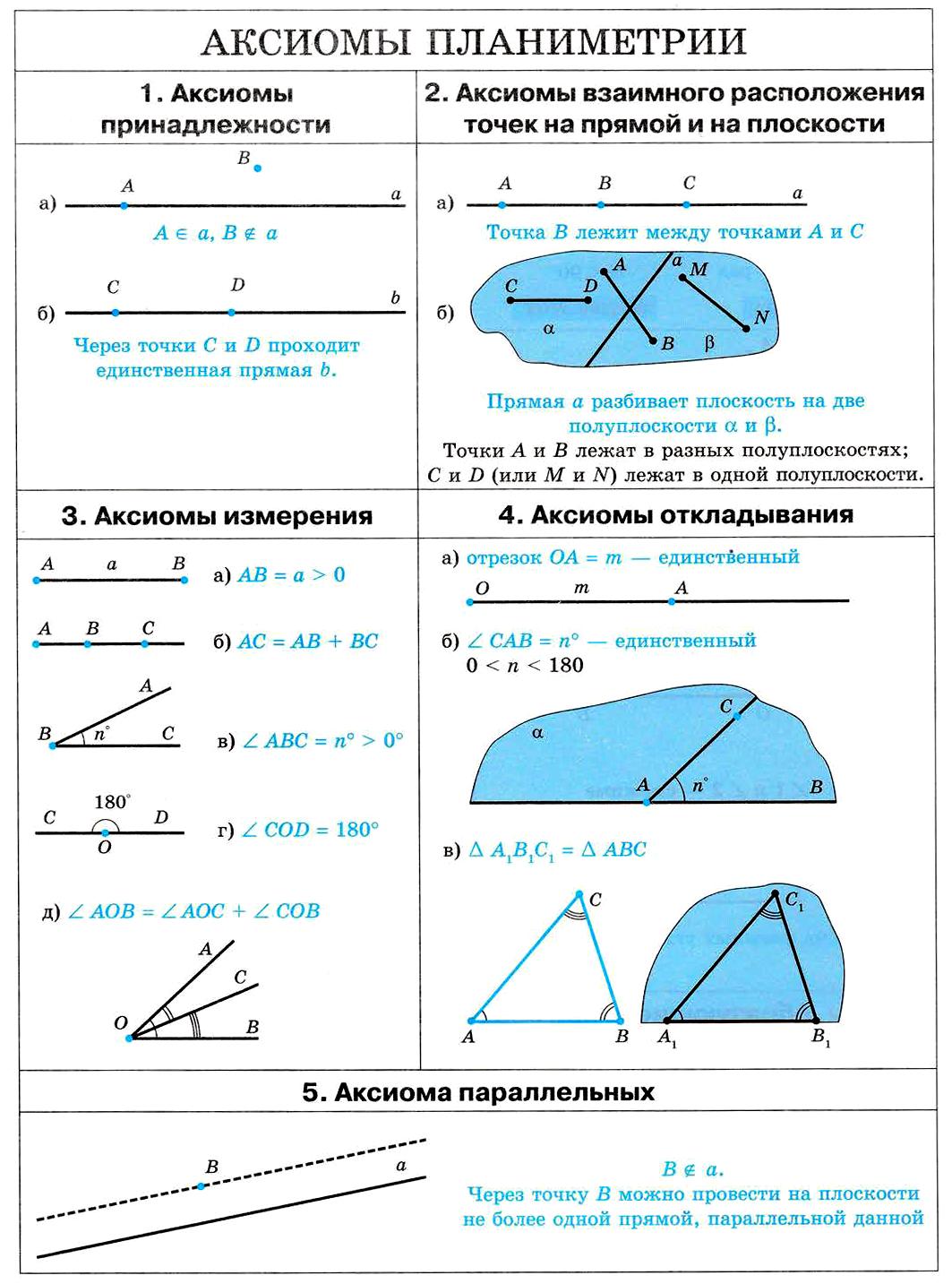
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы

Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой

03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника

Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
05. Равенство треугольников.
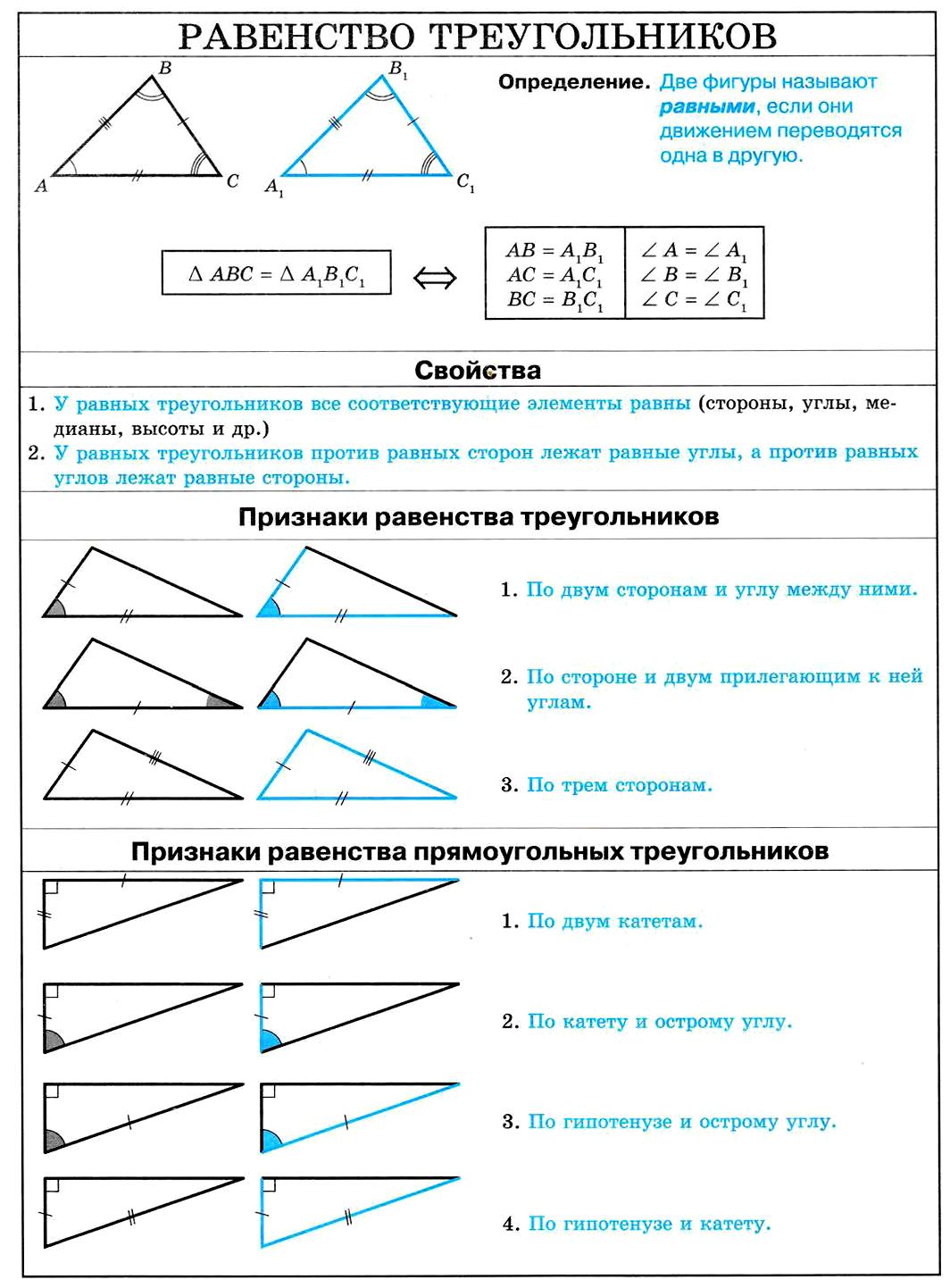
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.

Медиана треугольника. Свойства.
07. Биссектриса треугольника.

Биссектриса треугольника. Свойства
08. Высота треугольника
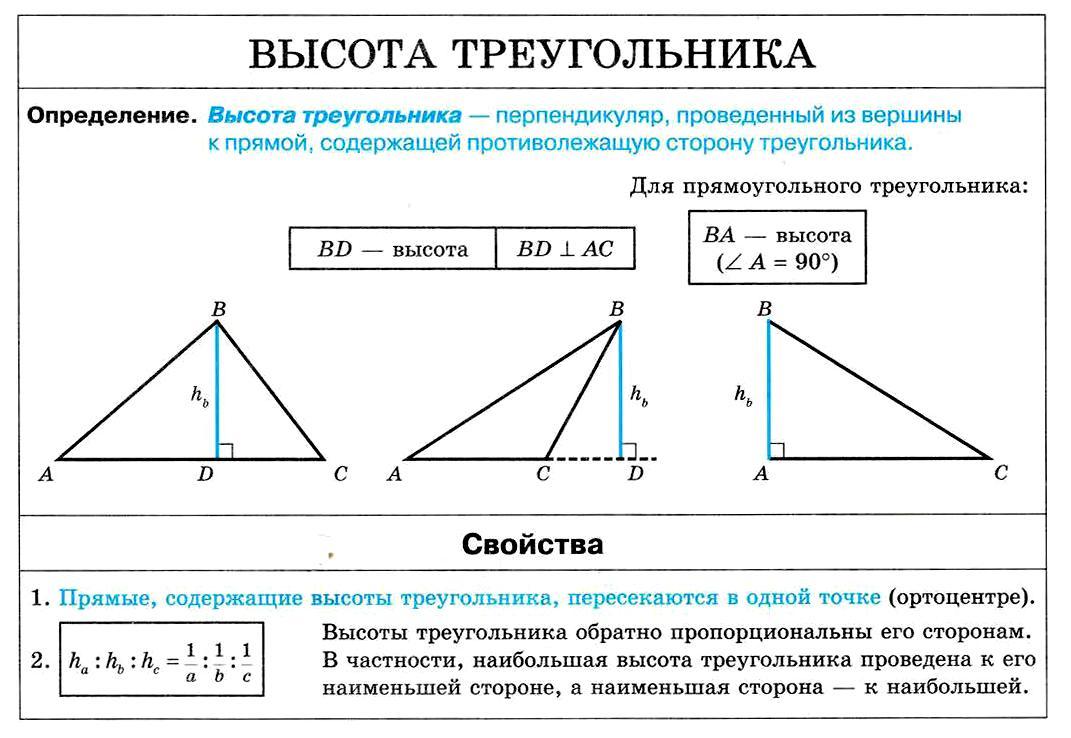
Высота треугольника. Свойства
09. Средняя линия треугольника

Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника

Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике

Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение

Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия

Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.

Подобие треугольников. Свойства. Признаки подобия треугольников
15. Параллелограмм и его виды.

Параллелограмм и его виды. Свойства. Признаки
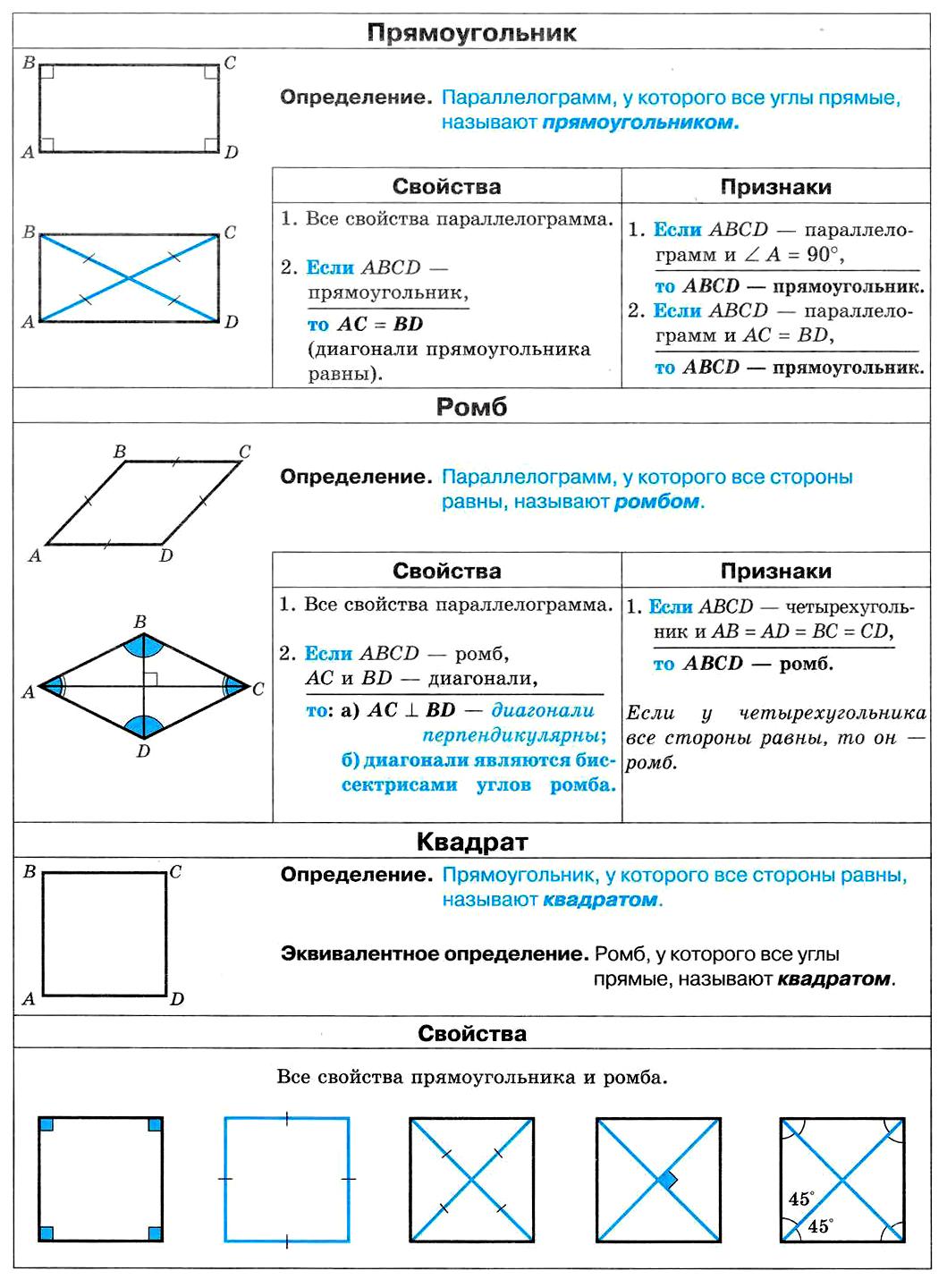
Прямоугольник. Ромб. Квадрат.
16. Трапеция

Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги

Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.

Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.

Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
20. Общие касательные двух окружностей.
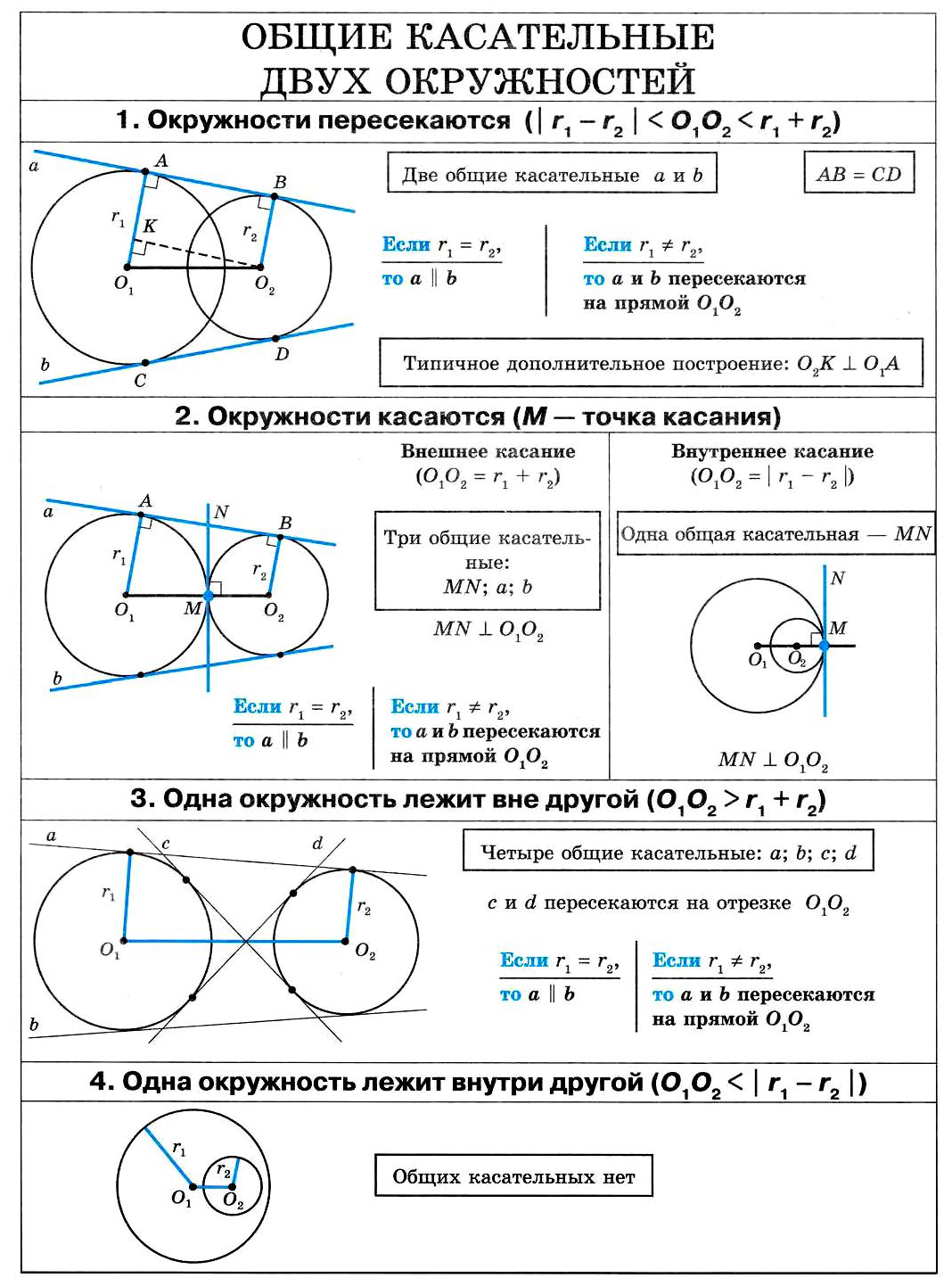
Общие касательные двух окружностей.
21. Углы в окружности.

Углы в окружности.
22. Длина окружности и её частей. Площадь круга и его частей
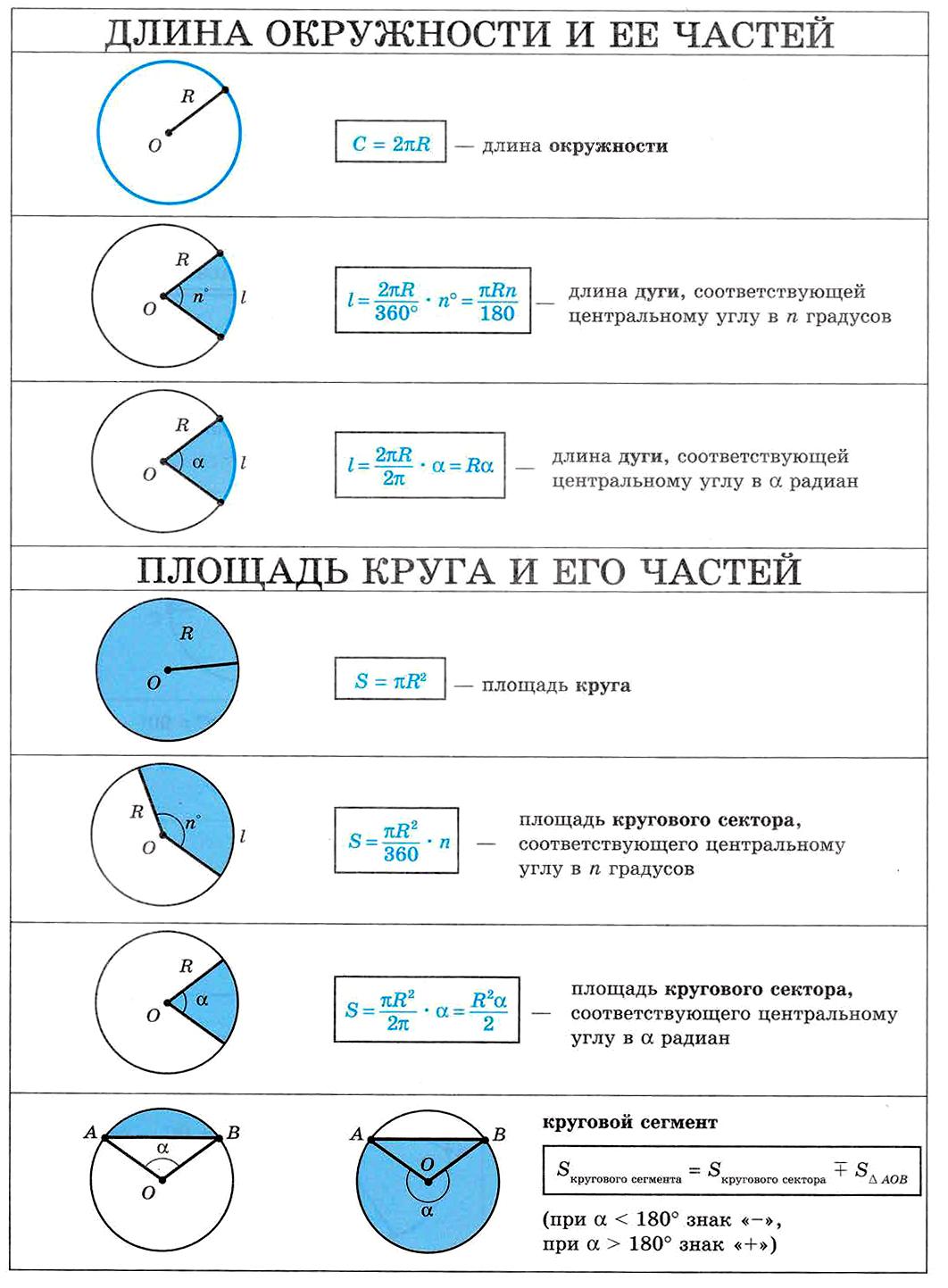
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.

Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.

Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники

Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.

27. Площади четырехугольников.
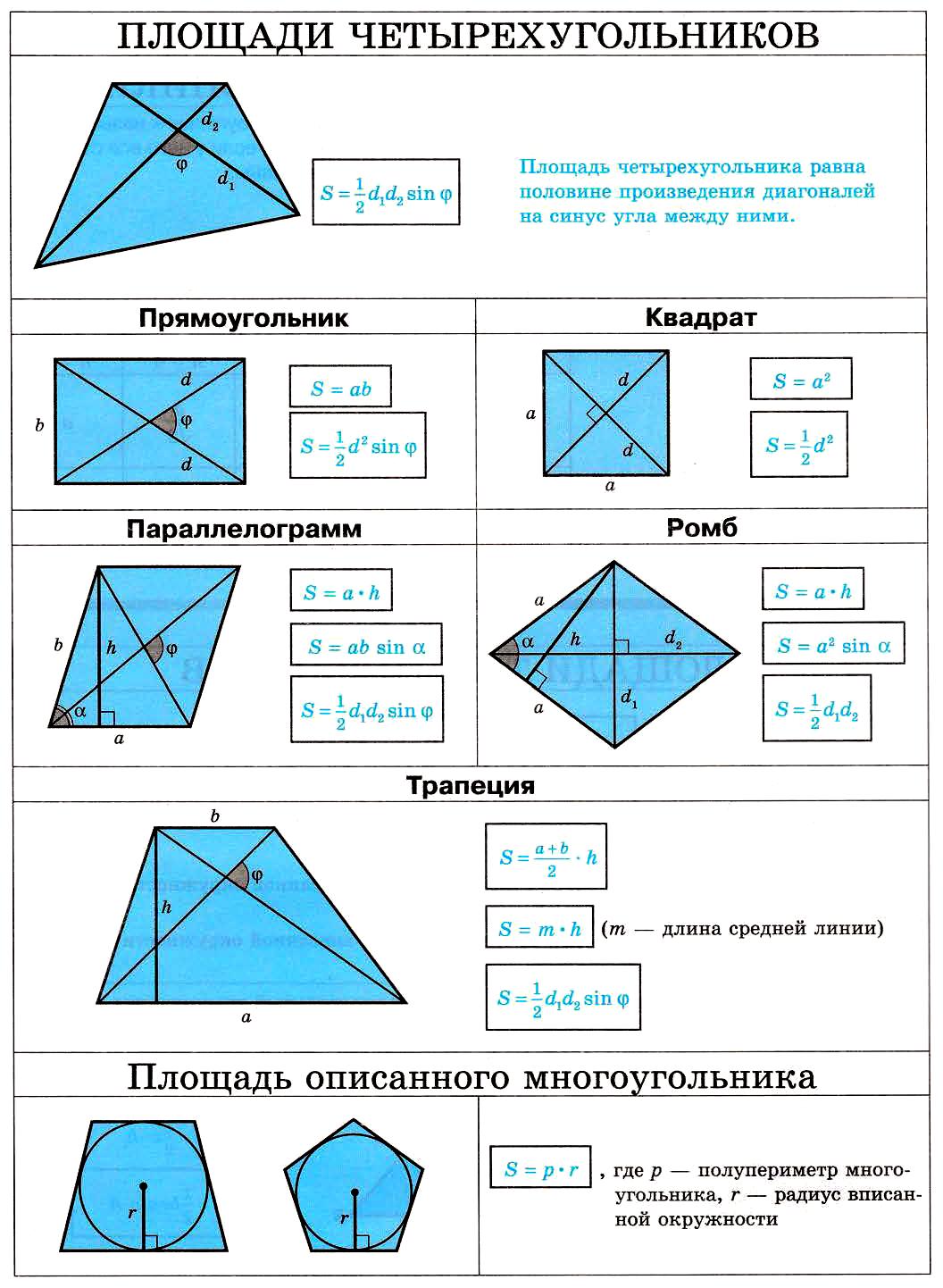
Площади четырехугольников. Площадь описанного многоугольника
2 Комментарии
Огромное спасибо за такую обширную базу по планиметрии. Конечно, сюда можно добавить ещё пару формул, но это самая полная шпаргалка по планиметрии, которую я знаю.
Отличный справочник по планиметрии! Благодарю!
Добавить комментарий Отменить ответ
Конспекты по геометрии:
7 класс
8 класс
9 класс
Найти конспект:
О проекте
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!
Читайте также:

