Энтропия это в термодинамике кратко

Обновлено: 30.06.2024

Первый закон термодинамики – закон сохранения тепловых процессов, устанавливающий связь между количеством теплоты Q и изменением ∆ U внутренней энергии и работой А , совершенной над внешними телами:

Исходя из закона, энергия не может быть создана или уничтожена: производится процесс передачи от одной системы к другой, принимая другую форму. Еще не было получено процессов, нарушающих первый закон термодинамики. Рисунок 3 . 12 . 1 показывает устройства, противоречащие первому закону.

Рисунок 3 . 12 . 1 . Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1 .

Обратимый и необратимый процессы

Первый закон термодинамики не устанавливает направления тепловых процессов. Опыты показывают, что большинство тепловых процессов протекают в одном направлении. Их называют необратимыми.

Если имеется тепловой контакт двух тел с разными температурами, тогда направление теплового потока направляется от теплого к холодному. Самопроизвольной передачи тепла от тела с низкой температуры к телу с высокой не наблюдается. Отсюда следует, что теплообмен с конечной разностью температур считается необратимым.

Обратимым процессом называется переход системы из одного равновесного расстояния в другое, которые возможно проводить в обратном направлении в той же последовательности промежуточных равновесных состояний. Она вместе с окружающими телами возвращаются к исходному состоянию.

Если система находится в состоянии равновесия во время процесса, она называется квазистатической.

Когда рабочее тело тепловой машины контактирует с тепловым резервуаром, температура которого неизменна во время всего процесса, то только изотермический квазистатический процесс считается обратимым, так как протекает с бесконечно малой разницей температур рабочего резервуара. Если имеется два резервуара, причем с разными температурами, тогда обратимым путем можно провести процессы на двух изотермических участках.

Так как адиабатический процесс проводится в обоих направлениях (сжатие и расширение), наличие кругового процесса с двумя изотермами и двумя адиабатами (цикл Карно) говорит о том, что это и есть единственный обратимый круговой процесс, где рабочее тело контактируется с двумя тепловыми резервуарами. Остальные при наличии 2 тепловых резервуаров считаются необратимыми.

Превращение механической работы во внутреннюю энергию считаются необратимыми при наличии силы трения, диффузии в газах и жидкостях, а процесс перемешивания по причине начальной разности давлений и так далее. Все реальные процессы считаются необратимыми, даже если значения будут максимально приближены к обратимым. Обратимые рассматриваются как пример реальных процессов.

Первый закон термодинамики не различает их. Правило требует от термодинамического процесса определенного энергетического баланса, но не говорит о том, возможен ли он. Установка направления прохождения процесса определяется вторым законом термодинамики. Его формулировка может звучать как запрет на определенные термодинамические процессы.

Второй закон был трактован У. Кельвином в 1851 .

В циклически действующей тепловой машине невозможно прохождение процесса, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.

Предположительно, машина с такими процессами могла бы получить название вечного двигателя второго рода.

При земных условиях могла бы быть отбита энергия Мирового океана и полностью превратилась бы в ее работу. Масса воды Мирового океана – 10 21 к г . Для его охлаждения хотя бы на 1 градус потребуется огромное количество энергии ≈ 10 24 Д ж , которое сравнимо с сжиганием 10 17 к г угля. Вырабатываемая энергия на Земле за год в 10 4 раз меньше. Отсюда и вывод о том, что вечный двигатель второго рода мало вероятен, как и двигатель первого, потому как оба они недопустимы, исходя из первого закона термодинамики.

Второй закон термодинамики

Формулировка 2 -го закона термодинамики была дана физиком Р. Клаузиусом.

Невозможно прохождение процесса, единственным результатом которого была бы передача энергии при помощи теплообмена от тела с низкой температуры к телу с более высокой.

Рисунок 3 . 12 . 2 объясняет процессы, которые запрещены вторым законом, но разрешены согласно первому. Они соответствуют трактовкам второго закона термодинамики.

Рисунок 3 . 12 . 2 . Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – вечный двигатель второго рода; 2 – самопроизвольный переход тепла от холодного тела к более теплому (идеальная холодильная машина).

Формулировки обоих законов считаются эквивалентными.

Когда тело без помощи внешних сил переходит при теплообмене от холодного к горячему, то возникает мысль о возможности создания вечного двигателя второго рода. Если такая машина получит количество теплоты Q 1 от нагревателя и отдаст холодильнику Q 2 , тогда совершается работа A = Q 1 - Q 2 . Если бы Q 2 самопроизвольно перешло к нагревателю, то конечный результат тепловой машины и идеальной холодильной машины выглядело бы таким образом Q 1 - Q 2 . Причем сам переход происходил бы без изменений холодильника. Отсюда вывод – комбинация тепловой машины и идеальной холодильной машины равноценна двигателю второго рода.

Прослеживается связь между вторым законом термодинамики и необратимостью реальных тепловых процессов. Энергия теплового движения молекул отлична от механической, электрической и так далее. Она способна превратиться в другой вид энергии только частично. Поэтому при наличии энергии теплового движения молекул любой процесс считается необратимым, так как полностью в обратном направлении он не осуществим.

Свойство, относящееся к необратимым процессам, говорит о том, что они проходят в термодинамически неравновесной системе, а результат получается в виде замкнутой системы, приближающейся к состоянию термодинамического равновесия.

Теоремы Карно

Имеются теоремы Карно, которые могут быть доказаны, исходя из второго закона термодинамики.

КПД тепловой машины, работающей при данных значениях температур нагревателя холодильника, не может иметь значение больше, чем КПД действия машины, работающей согласно обратимому циклу Карно с теми же значениями температур нагревателя и холодильника.

КПД действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.

Отсюда следует, что КПД действия машины с циклом Карно считается максимальным.

η = 1 - Q 2 Q 1 ≤ η m a x = η К а р н ю = 1 - T 2 T 1 .

Знак равенства данной записи говорит об обратимости процесса. Если машина работает по циклу Карно, тогда:

Q 2 Q 1 = T 2 T 1 или Q 2 T 2 = Q 1 T 1 .

Знаки Q 1 и Q 2 всегда отличаются независимо от направления цикла. Поэтому получаем:

Q 1 T 1 + Q 2 T 2 = 0 .

Рисунок 3 . 12 . 3 говорит о том, что данное соотношение обобщается и представляется в виде последовательности малых изометрических и адиабатических участков.

Рисунок 3 . 12 . 3 . Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков.

Полный обход замкнутого обратимого цикла имеет вид:

∑ ∆ Q i T i = 0 (обратимый цикл).

Откуда ∆ Q i = ∆ Q 1 i + ∆ Q 2 i – количество теплоты, полученное рабочим телом на двух изотермических участках с температурой T i . Чтобы данный цикл провести наоборот, нужно рабочее тело сконтактировать со многими тепловыми резервуарами с T i .

Энтропия

Отношение Q i T i получило название приведенного тепла. Формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Благодаря ей вводится еще одно понятие – энтропия, обозначаемая S . Ее открыл Р. Клаузиус в 1865 году.

При переходе из одного равновесного состояние в другое изменяется и ее энтропия. Разность энтропий двух состояний равняется приведенному теплу, полученному системой во время обратного перехода состояния.

∆ S = S 2 - S 1 = ∑ ( 1 ) ( 2 ) ∆ Q i о б р T .

Если рассматривается адиабатический процесс ∆ Q i = 0 , тогда энтропия S не изменяется.

Изменение энтропии ∆ S во время перехода в другое состояние фиксируется как формула:

∆ S = ∫ ( 1 ) ( 2 ) d Q о б р T .

Определение энтропии достаточно точное. Разность ∆ S двух состояний системы подразумевает физический смысл. Если имеется необратимый переход, а необходимо найти энтропию, тогда нужно придумать обратимый процесс, который свяжет начальное и конечное состояние. После этого перейти к нахождению приведенного тепла, полученного системой.

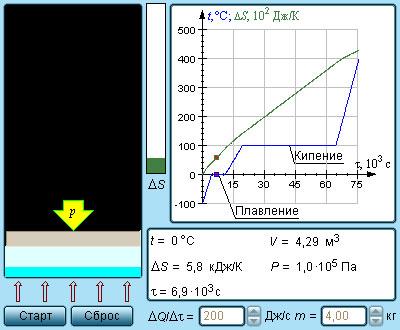
Рисунок 3 . 12 . 4 Модель энтропии и фазовых переходов.

Рисунок 3 . 12 . 5 показывает необратимый процесс расширения шага с отсутствием теплообмена. Равновесными считаются начальное и конечное значение, изображаемые на диаграмме p , V . Точки a и b соответствуют состояниям и располагаются на одной изотерме. Чтобы найти ∆ S , следует перейти к рассмотрению обратимого изотермического перехода из a в b . При изопроцессе газ получает определенное количество теплоты окружающих тел Q > 0 , тогда при необратимом расширении энтропия возрастет до ∆ S > 0 .

Еще одним примером необратимого процесса считается теплообмен при конечной разности температур. Рисунок 3 . 12 . 6 и показывает два тела, заключенные в адиабатическую оболочку, где начальные температуры обозначаются как T 1 и T 2 T 1 . Течение процесса теплообмена способствует выравниванию температур. Очевидно, что теплое тело отдает, а холодное принимает. Холодное тело превосходит по модулю приведенное тепло, отдаваемое горячим. Отсюда вывод – изменение энтропии в замкнутой системе необратимого процесса ∆ S > 0 .

Рисунок 3 . 12 . 6 . Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии Δ S > 0 .

Все самопроизвольно протекающие процессы в изолированных термодинамических процессах характеризуются ростом энтропии.

Обратимые процессы имеют постоянную энтропию ∆ S ≥ 0 . Соотношение называют законом возрастания энтропии.

При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо не меняется, либо возрастает.

Наличие энтропии говорит о самопроизвольно протекающем процессе, а ее рост – приближение всей системы к термодинамическому равновесию, где S принимает максимальное значение. Возрастание энтропии можно трактовать как формулировку второго закона термодинамики.

В 1878 году Л. Больцман дал вероятностное определение понятию энтропии, так как было предложено рассматривать ее в качестве меры статистического беспорядка замкнутой термодинамической системы. Все самопроизвольно протекающие процессы в таких системах приближают ее к равновесному состоянию, так как сопровождаются ростом энтропии, и направляют в сторону увеличения вероятности состояния.

Если состояние макроскопической системы содержит большое число частиц, то его реализация может предусматривать несколько способов.

Термодинамическая вероятность W системы – это количество способов, которыми реализуется данное состояние макроскопической системы, макросостояний, осуществляющих его.

Из определения имеем, что W ≫ 1 .

При наличии 1 м о л ь газа в емкости существует число N способов размещения молекулы по двум половинам емкости: N = 2 N А , где N А - число Авогадро. Каждое из них – это микросостояние.

Одно из них соответствует случаю с молекулами, собранными в одной половине сосуда. Вероятность такого события приравнивается к нулю. Большое количество состояний соответствует такому, где молекулы распределяются равномерно по всей площади емкости.

Тогда равновесное состояние является наиболее вероятным.

Равновесное состояние считается состоянием наибольшего беспорядка в термодинамической системе с максимальной энтропией.

Исходя из трактовок Больцмана, энтропия S и термодинамическая вероятность W связаны:

S = k · ln W , где k = 1 , 38 · 10 - 23 Д ж / К является постоянная Больцмана. Отсюда следует, что определение энтропии определяется логарифмом числа микросостояний. Именно они способствуют реализации данного макросостояния. Тогда энтропия может быть рассмотрена в качестве меры вероятности состояния термодинамической системы.

Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Их называют флуктуациями.

В системах с большим числом частиц отклонения от состояния равновесия имеют достаточно малую вероятность на существование.

$\frac<\delta Q> Понятие энтропии ввел в XIX веке Р. Клаузиус. Энтропия ( ) – это функция состояния, в обратимом процессе дифференциалом которой является величина$
:

$dS=\frac<\delta Q> \qquad (1)$

где – количество теплоты, полученное термодинамической системой в ходе обратимого процесса; – термодинамическая температура системы.

В любом обратимом круговом процессе изменение энтропии равно нулю:

Энтропия системы, которая совершает необратимый цикл, растет:

Выражения (2) и (3) относятся только к замкнутым системам, в том случае, если система обменивается теплотой с внешней средой, то энтропия может вести себя как угодно. Формулы (2) и (3) в единстве представляют собой неравенство Клаузиуса:

которое говорит о том, что в замкнутых системах при обратимых процессах, энтропия остается постоянной, а в необратимых процессах она растет.

В случае равновесного перехода из одного состояния в другое, в соответствии с определением энтропии (1), имеем:

$\Delta S=S_2-S_1=\int^2_1<\frac<\delta Q> =\int^2_1>> \qquad (5)$

где по первому началу термодинамики. – изменение внутренней энергии термодинамической системы; – работа выполняемая системой. В формуле (5) подынтегральное выражение и пределы интегрирования следует выразить, используя параметры, которые характеризуют процесс, происходящий в термодинамической системе. Выражение (5) определяет энтропию с точностью до аддитивной постоянной. Физический смысл несет изменение энтропии, а не сама энтропия.

Свойство энтропии

Энтропия имеет свойство аддитивности: Энтропия совокупности тел равна сумме энтропий каждого тела, которое входит в систему.

Глубинный смысл энтропии открывает статистическая физика. Больцман установил, что энтропия системы связана с термодинамической вероятностью ( ):

где – постоянная Больцмана.

Напомним, что термодинамической вероятностью называют число способов, при помощи которых можно реализовать макросостояние термодинамической системы, или количество микросостояний, которые реализуют данное макросостояние.

В соответствии с (6) энтропия — это мера вероятности состояния термодинамической системы. Иногда, исходя из статистического толкования энтропии, говорят, что энтропия – мера неупорядоченности системы.

Примеры решения задач

Задание	Найдите изменение энтропии в процессах идеального газа.
Решение	В качестве основы для решения задачи используем формулу:

$\Delta S=\int^2_1<\frac<dU+\delta A> \qquad (1.1)>$

Для идеального газа изменение внутренней энергии:

$dU=\frac \nu RdT\ \qquad (1.2)$

Работа газа по определению равна:

Или, если учесть, что из уравнения Менделеева – Клайперона:

$p=\frac<\nu RT> \qquad (1.4)$

получаем, что элементарная работа идеального газа равна:

$\delta A=\frac<\nu RT> dV \qquad (1.5)$

Подставим выражения (1.2) и (1.5) в определение изменения энтропии (1.1), получим:

$\Delta S=\int^<T_2> _\frac+\int^_>=\nu R(\frac<\ln \left(\frac<T_2>\right)+<\ln \left(\frac\right))>>> \qquad (1.6)$

Изменение энтропии при переходе из одного состояния в другое для идеального газа не зависит от процесса перехода.

$\Delta S_<1-2-3> =\Delta S_=S_3-S_1 \qquad (2.1)$

В качестве основы для решения задачи воспользуемся формулой, которую мы получили в примере 1:

$\Delta S=\nu R(\frac <\ln \left(\frac<T_3>\right)+<\ln \left(\frac<V_3>\right))>> \qquad (2.2)$

Для изохорного процесса выражение (2.2) принимает вид:

$\Delta S=\nu R\frac <\ln \left(\frac<T_3>\right)> \qquad (2.3)$

Так как процесс 3-1 изохорный, то для него справедлив закон Шарля:

$\frac<T_3> =\frac \qquad (2.4)$

Воспользуемся уравнением адиабаты для процесса 1-2, и учтем, что процесс 2-3 изобарный, запишем:

$p_1V^<\gamma > _1=p_2V^<\gamma >_2=p_3V^<\gamma >_2\to \frac=<\left(\frac<V_1>\right)>^<\gamma >=n^ <-\gamma >\qquad (2.5)$

Подставим правую часть выражения (2.5) вместо отношения " width="16" height="24" />
в формулу (2.3), примем во внимание, что " width="62" height="22" />
имеем:

$\Delta S=\nu R\frac <\ln \left(\frac<T_3>\right)=\nu R\frac\left(-\gamma \right)<\ln n=-\nu R\frac<i+2>><\ln (n)>>$

Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.

Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).

Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.

Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.

хотя вы, скорее всего, лучше знакомы с уравнением Клапейрона — Менделеева pV = νRT — это то же самое уравнение, только с добавлением пары констант, чтобы вас запутать. Чем больше микросостояний отвечают данному макросостоянию, то есть чем больше частиц входят в состав нашей системы, тем лучше уравнение состояния её описывают. Для газа характерные значения числа частиц равны числу Авогадро, то есть составляют порядка 10 23 .

Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.

Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.

Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.

Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.

Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.

Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад.

Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.

И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.

Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?

Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.

Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.

Термодинами́ческая энтропи́я S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Содержание

Термодинамическое определение энтропии

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом . Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:

$<\displaystyle \Delta S=<\frac <\Delta Q> >.>$

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного ,

$<\displaystyle dS> где$
- приращение (дифференциал) энтропии, а " width="" height="" />
- бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

$<\displaystyle \delta Q> Поскольку энтропия является функцией состояния, в левой части равенства стоит её функцией процесса, в котором эта теплота была передана, поэтому$
считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана

где константу k=1,38•10 –23 Дж/К мы знаем теперь как постоянную Больцмана, а Ω является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как Ω может быть только натуральным числом (1,2,3,…), то энтропия Больцмана должна быть положительной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный "беспорядок", т.к. при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно [1] .

Рассмотрим оба пункта более подробно.

Рассмотрим пример термодинамической системы - распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример - учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим максимуму энтропии, будет упорядоченное кристаллическое состояние, а совсем не "хаос". (Термин "хаос" здесь понимается в смысле беспорядка - в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель - совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, т.е. - беспорядок согласно вышеуказанному определению. Но данный "беспорядок" вовсе не соответствует "беспорядку" в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из "хаотичной" жидкости идёт параллельно с увеличением энтропии.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т.н. "демона Максвелла". Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т.н. "демон". "Демон" мог измерять скорость отдельных летящих молекул, и т.о. избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные - в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы "демон" должен был бы получить информацию о её скорости. Но всякое получение информации - материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ, проведённый, например, в [2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспрелением молекул "демоном".

Однако многие учёные стали отождествлять информацию с "отрицательной энтропией" ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер [3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Безусловно, этот пример также некорректен, т.к. система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах

$<\displaystyle dS_<o> =>>>->>>.>$

$<\displaystyle dS=dS_ +dS_.>$

Если всё время , то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если " width="" height="" />
, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру >" width="" height="" />
внешнего потока тепла в температуру >" width="" height="" />
уходящего из системы потока тепла.

Измерение энтропии

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

$<\displaystyle \Delta S=\int <\frac <C_<X> >>dT>$

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

$<\displaystyle S(P,V)=S(P,V_<0> )+\int _<T(P,V_<0>)>^(P,V(T,P))>>dT>$

Построение графика изменения энтропии

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P-V:

$<\displaystyle S=nR\ \ln(1+P^<C_<V> \over R>V^ \over R>)>$

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что C_V и C_P постоянные, что на самом деле не так.

Понятие энтропии — одно из наиболее сложных и многогранных. Постараемся разобраться, что это такое.

Что такое энтропия

Понятие энтропии используется в различных областях знаний. Наиболее общее ее определение можно выразить следующим образом:

Энтропия — мера хаоса, беспорядка, степень неопределенности.

Впервые этот термин был использован немецким физиком Рудольфом Клаузиусом в 1865 году. Тогда он имел узкое значение одной из физических переменных.

Энтропия в термодинамике

Термодинамическая энтропия — физическая величина, которая описывает термодинамическую систему, термические явления и свойства макроскопических объектов.

Энтропия — это переменная, описывающая физическое состояние системы (обозначается буквой S).

Объяснить понятие энтропии можно на следующем примере. Представьте кусок горячего металла, чье тепло распространяется по окружающей среде. Также рядом с этим металлом витают пять молекул газа. Металл передаст пять квантов тепла. Значит ли это, что каждая молекула газа получит по одному кванту? Нет. Возможно, три молекулы получат по одному кванту, одна — два, а последняя — ни одного. Или двум молекулам перейдут два кванта, одной — один, а две другие не получат ни одной. Вариантов развития событий в таком случае 126.

Каждая из возможных комбинаций называется микросостоянием, а общий уровень энергии — макросостоянием. Тогда энтропия — значение числа способов, мера вероятностей распределения энергии между молекулами в системе.

Формулировка закона энтропии в термодинамике

Исходным положением термодинамики является постулат о равновесии, суть которого заключается в том, что любая изолированная система со временем приходит в состояние термодинамического равновесия и самопроизвольно выйти из него не может.

Второй закон термодинамики связан с понятием энтропии. Он говорит о том, что энтропия Вселенной возрастает.

Есть два классических определения второго закона:

Кельвина и Планка. Нет циклического процесса, который мог бы извлекать количество теплоты при определенной температуре и полностью превращает эту теплоту в работу.
Клаузиуса. Нет процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому.

Оба определения основываются на первом законе термодинамики, согласно которому энергия убывает.

Можно сделать следующие выводы:

100% энергии не может быть преобразовано в работу;
энтропия может быть выработана, но не может быть уничтожена.

Энтропия в экономике

В экономике понятие энтропии объясняет непредвиденное развитие рынка. То есть экономическая цель не достигнута по причине того, что система оказалось неупорядоченной, неинформативной и так далее.

Энтропия — количественный показатель беспорядка, мера излишне выполненной работы для достижения цели, доля побочных явлений и процесс какой-либо деятельности.

Движение денег в экономике происходит ассиметрично. Также если предположить, что деньги являются аналогом энергии, то второй закон термодинамики можно адаптировать следующим образом: не существует такой экономической системы, единственным итогом деятельности которой будет переход денег от рынка производителей к рынку потребителей.

Общая формула для экономической энтропии выглядит так:

$dS = d Financial Resources / Price For The Resources $

Энтропия в коммуникации

Энтропия — информационная неопределенность в системе.

Информация — противоположность энтропии, возможность уменьшения беспорядка. То есть чем более информации содержит система, тем более она является упорядоченной.

Примеры энтропии в разных сферах жизни

Рассмотрим данное понятие на примерах из жизни.

Представьте, что у вашего друга в руках десять игральных кубиков. Он их бросил и сказал вам, что сумма всех выпавших чисел равна 30. Но вы не знаете, какие конкретно числа ему выпали. Именно этой информации вам не хватает.

Тогда общая сумма в этом случае будет макросостоянием, а возможные комбинации чисел — микросостоянием. Для данной ситуации существует 2 930 455 микросостояний.

Частично снять вашу энтропию друг сможет, если сообщит, например, что сумма первой половины чисел равна 17, а второй — 13. Для первой половины есть 720 возможных комбинаций, а для второй — 420. Тогда для всего макросостояния существует 327 600 вариантов.

Как пример системы, увеличивающей энтропию, можно рассмотреть шкаф. Вы аккуратно сложили в него вещи, то есть упорядочили систему. Но даже если шкаф будет закрыт на долгие годы, одежда начнет разлагаться. То есть система будет увеличивать показатель своей энтропии.

Если нужна работа, связанная с понятием энтропии, или по какой-либо другой теме, обращайтесь в ФениксХелп.

Читайте также: