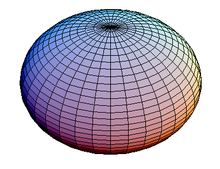
Эллипсоид вращения это кратко

Обновлено: 06.07.2024

В математике , эллипсоид вращения или сфероида является поверхность вращения получается вращающимся в пространстве А.Н. эллипса вокруг одной из его осей . Как и любой эллипсоид , это квадратная поверхность , то есть описывается уравнением степени 2 по каждой координате в декартовой системе координат .

Выражение может также иногда обозначать ограниченный объем, ограниченный этой поверхностью, в частности, для описания физических объектов, таких как Земля или атомные ядра .

Эллипсоид вращения может быть:

удлиненный (или продолговатый, по- английски : вытянутый ), если ось вращения является главной осью (большая ось), что придает ей форму мяча для регби ;
сплюснутый (по-английски: сплющенный ) в противном случае (примерно как поверхность Земли );
сферической , в частном случае, когда образующий эллипс представляет собой круг.

Резюме

Характеристики

Параметризация

В плоскости сечения, содержащей ось вращения, след эллипсоида представляет собой эллипс, параметризованный в цилиндрических координатах углом в центре θ, изменяющимся между 0 и 2π, в виде:

где p - полярный радиус (длина полуоси вращения), q - экваториальный радиус.

Таким образом, эллипсоид вращения параметризуется в декартовых координатах в соответствующей ортонормированной системе координат: < Икс ( θ , ϕ ) знак равно q потому что ⁡ ( θ ) потому что ⁡ ( ϕ ) y ( θ , ϕ ) знак равно q потому что ⁡ ( θ ) грех ⁡ ( ϕ ) z ( θ , ϕ ) знак равно п грех ⁡ ( θ ) x (\ theta, \ phi) = q \ cos (\ theta) \ cos (\ phi) \\ y (\ theta, \ phi) = q \ cos (\ theta) \ sin (\ phi) \\ z (\ theta, \ phi) = p \ sin (\ theta) \ end > \ right.> где угол поворота ϕ изменяется от 0 до π .

Эта параметризация не уникальна.

Декартово уравнение

С помощью этих обозначений, эллипсоид вращения появляется как образ сферы радиуса д с помощью сродства с отношением р / д , параллельной оси вращения.

Внутренний объем

Предыдущее свойство позволяет вывести выражение внутреннего объема, ограниченного эллипсоидом вращения: V знак равно 4 3 π п q 2 > \ pi pq ^ > где p - полярный радиус, q - радиус на экваторе.

Область

Площадь эллипсоида вращения задается двумя разными формулами в зависимости от того, является ли ось вращения эллипса его большой осью или малой осью. Чтобы устранить двусмысленность, выбранные обозначения являются обычными обозначениями для эллипсов: полудлина большой оси обозначена a , полудлина малой оси обозначена b , эксцентриситет e задается формулой: е знак равно в 2 - б 2 в . -b ^ >> >.>

Если a = b , площадь рассчитывается по следующей формуле: В знак равно 4 π р 2 , ,> где R = a = b .
Когда ось вращения является малой осью, эллипсоид сплющен, его полярный радиус строго меньше его экваториального радиуса, а площадь задается формулой: В знак равно 2 π в 2 + π б 2 е пер ⁡ ( 1 + е 1 - е ) . + >> \ ln \ left ( > \ верно).>
Когда ось вращения является большой осью, эллипсоид вытянут, его полярный радиус строго больше, чем его экваториальный радиус, а площадь задается формулой: В знак равно 2 π б 2 + 2 π в б е Arcsin ⁡ ( е ) . + > \ arcsin (e).>

Использование одной из двух последних формул в случае, когда a = b, приводит к делению на ноль вида 0/0, поскольку эксцентриситет e равен 0 . Обратите внимание, что когда e стремится к 0 , эти два выражения стремятся к 4π R 2 .

Приложения

В физике появляется несколько примеров эллипсоидов вращения . Например, жидкая масса, подверженная собственному гравитационному притяжению и вращающаяся сама по себе, образует сплюснутый эллипсоид. Другой пример - деформация Земли и особенно уровня Мирового океана в вытянутый эллипсоид под действием внешнего гравитационного поля, в результате чего возникло явление приливов и отливов .

Эллипсо́ид враще́ния (сферо́ид) — это фигура вращения в трёхмерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей.

Эллипсоид вращения является частным случаем эллипсоида, две из трёх полуосей которого имеют одинаковую длину ():

$\frac<x^2></p> <p>^2>+\frac^2>+\frac=\frac+\frac=1.\,\!$

В частном случае, когда все три полуоси равны, исходный эллипс представляет собой окружность, а эллипсоид вращения вырождается в сферу.

Содержание

Вытянутый эллипсоид вращения

Вытянутый эллипсоид вращения можно также определить как геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек (фокусов) постоянна.

Зеркало в виде вытянутого эллипсоида вращения обладает следующим свойством: лучи света, исходящие из одного из фокусов эллипсоида, после отражения соберутся в другом фокусе.

Сплюснутый эллипсоид вращения

Сплюснутый эллипсоид вращения можно также определить как геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна.

Основные формулы

$o\!\varepsilon\,\!$

Здесь - угловой эксцентриситет:

\right)=2\arctan\left(\sqrt>\right)\quad\mathrm<>,\,\!" width="" height="" />
(сжатый) \right)=2\arctan\left(\sqrt>\right)\quad\mathrm<>;\,\!" width="" height="" />
(вытянутый) (sin(oε) часто выражается как эксцентриситет, "e")

Примеры

$<\frac</p> <p>Форма Земли — в хорошем приближении представляет собой сплюснутый эллипсоид вращения с \approx>>$
.

Применение

Свойство вытянутого эллипсоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Грегори и в антеннах Грегори.

Примечания

↑L. Russo The forgotten revolution. — Springer, Berlin, 2004. — P. 180.

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Эллипсоид вращения" в других словарях:

эллипсоид вращения — sukimosi elipsoidas statusas T sritis fizika atitikmenys: angl. ellipsoid of revolution vok. Drehellipsoid, n; Rotationsellipsoid, n rus. эллипсоид вращения, m pranc. ellipsoïde de révolution, m … Fizikos terminų žodynas

ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка

Эллипсоид — вращения Эллипсоид поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых коор … Википедия

Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь

Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия

Эллипсоид нормальный — Нормальный эллипсоид: эллипсоид вращения, создающий гравитационное поле, максимально близкое к гравитационному полю Земли. Источник: ГЕОГРАФИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ . КООРДИНАТНАЯ ОСНОВА. ОБЩИЕ ТРЕБОВАНИЯ. ГОСТ Р 52572 2006 (утв. Приказом … Официальная терминология

эллипсоид — а; м. [от греч. elleipsis выпадение, опущение и eidos вид] Матем. Поверхность, образуемая вращением эллипса (1.Э.; 1 зн.) вокруг одной из своих осей. ◁ Эллипсоидный, ая, ое. * * * эллипсоид замкнутая поверхность (2 го порядка). Эллипсоид можно… … Энциклопедический словарь

Эллипсоид* — Поверхность второго порядка, замкнутая, имеющая центр и пересекаемая всякой плоскостью по эллипсам или кругам, называется Э. На прилагаемом чертеже изображен Э. с тремя неравными главными взаимно перпендикулярными полуосями: большой а = OA,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Эллипсоид — Поверхность второго порядка, замкнутая, имеющая центр и пересекаемая всякой плоскостью по эллипсам или кругам, называется Э. На прилагаемом чертеже изображен Э. с тремя неравными главными взаимно перпендикулярными полуосями: большой а = OA,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь

Эллипсо́ид враще́ния (сферо́ид) — поверхность вращения в трёхмерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей.

Эллипсоид вращения является частным случаем эллипсоида, две из трёх полуосей которого имеют одинаковую длину

где — положительные параметры, удовлетворяющие неравенствам .

Если точка принадлежит эллипсоиду (4.46), то координаты точек при любом выборе знаков также удовлетворяют уравнению (4.46). Поэтому эллипсоид (4.46) симметричен относительно координатных плоскостей, координатных осей и начала координат. Начало координат называют центром эллипсоида (4.46). Шесть точек пересечения эллипсоида с координатными осями называются его вершинами, а три отрезка координатных осей, соединяющих вершины, — осями эллипсоида. Оси эллипсоида, принадлежащие координатным осям , имеют длины соответственно. Если — малой полуосью эллипсоида. Если полуоси не удовлетворяют условиям , то уравнение (4.46) не является каноническим. Однако при помощи переименования неизвестных можно всегда добиться выполнения неравенств .

Плоские сечения эллипсоида

Подставляя линии пересечения эллипсоида с координатной плоскостью . Это уравнение в плоскости определяет эллипс Линии пересечения эллипсоида с другими координатными плоскостями также являются эллипсами. Они называются главными сечениями (главными эллипсами) эллипсоида.

Рассмотрим теперь сечение эллипсоида плоскостью, параллельной какой-нибудь координатной плоскости, например . Подставляя — произвольная постоянная (параметр), в уравнение (4.46), получаем

При уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость . Следовательно, плоскости касаются эллипсоида в его вершинах . При , разделив обе части уравнения (4.47) на , получаем уравнение эллипса полуосями . Следовательно, сечение эллипсоида плоскостью представляет собой эллипс.

Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).

Эллипсоиды вращения

Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом ). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при являются окружностями. Следовательно, сечения эллипсоида плоскостями представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси эллипс заданный в плоскости (рис.4.41,а).

Если , то все сечения эллипсоида (4.46) плоскостями будут окружностями с центрами на оси абсцисс. Такой эллипсоид можно получить, вращая вокруг оси эллипс (рис.4.41,б).

Если все полуоси эллипсоида равны , то он представляет собой сферу радиуса , называется трехосным (или общим).

1. Плоскости определяют в пространстве основной прямоугольный параллелепипед , внутри которого находится эллипсоид (см. рис.4.40,б). Грани параллелепипеда касаются эллипсоида в его вершинах.

2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.

3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.

В самом деле, если точка принадлежит эллипсоиду, то точки с координатами при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).

О сфероидах при культивировании клеток см. 3D клеточная культура. Для вращающихся равновесных сфероидов см. Сфероид маклорена.

Сфероиды с вертикальными осями вращения

сплюснутый		вытянутый

А сфероид, или эллипсоид вращения, это квадрика поверхность получено вращающийся ан эллипс около одной из его главных осей; другими словами, эллипсоид с двумя равными полудиаметры. Сфероид имеет круговая симметрия.

Если эллипс вращается вокруг своей большой оси, результатом будет вытянутый (удлиненный) сфероид, имеющий форму Американский футбол или регби мяч. Если эллипс вращается вокруг своей малой оси, результатом будет сплюснутый (сплющенный) сфероид, имеющий форму чечевица. Если образующий эллипс представляет собой круг, результатом будет сфера.

Благодаря комбинированному воздействию сила тяжести и вращение, то фигура Земли (и всего планеты) не совсем сфера, а немного сплющенный в направлении его оси вращения. По этой причине в картография и геодезия Землю часто аппроксимируют сплюснутым сфероидом, известным как опорный эллипсоид, вместо сферы. Электрический ток Мировая геодезическая система модель использует сфероид с радиусом 6 378,137 км (3 963,191 миль) в Экватор и 6,356,752 км (3,949,903 миль) на полюса.

Слово сфероид Первоначально означало "приблизительно сферическое тело", допускающее неоднородности даже за пределами двух- или трехосной эллипсоидальной формы, и именно так этот термин используется в некоторых более старых работах по геодезии (например, имея в виду усеченное сферическое гармоническое расширение Земли ). [1]

Содержание

Уравнение

Уравнение трехосного эллипсоида с центром в начале координат с полуосями а , б и c по координатным осям

Уравнение сфероида с z как ось симметрии дается установкой а = б :

Полуось а - экваториальный радиус сфероида, а c - расстояние от центра до полюса по оси симметрии. Возможны два случая:

c : сплюснутый сфероид
c >а : вытянутый сфероид

Случай а = c сводится к сфере.

Свойства

Площадь

Сплюснутый сфероид с c имеет площадь поверхности

Сплюснутый сфероид создается вращением вокруг z - ось эллипса с большой полуосью а и малая полуось c , следовательно е может быть идентифицирован как эксцентриситет. (Увидеть эллипс.) [2]

Вытянутый сфероид с c > а имеет площадь поверхности

Вытянутый сфероид создается вращением вокруг z - ось эллипса с большой полуосью c и малая полуось а ; следовательно, е снова может быть идентифицирован как эксцентриситет. (Увидеть эллипс.) [3]

Эти формулы идентичны в том смысле, что формула для S_{сплюснутый} может использоваться для расчета площади поверхности вытянутого сфероида и наоборот. Однако, е затем становится воображаемый и больше не может напрямую отождествляться с эксцентриситетом. Оба эти результата могут быть представлены во многих других формах, используя стандартные математические тождества и отношения между параметрами эллипса.

Объем

Кривизна

Если сфероид параметризован как

где β это уменьшенный или параметрическая широта, λ это долгота, и − π / 2 π / 2 и −π , то его Гауссова кривизна является

Обе эти кривизны всегда положительны, так что каждая точка сфероида эллиптическая.

Соотношение сторон

В соотношение сторон сплющенного сфероида / эллипса, c : а , - отношение полярной длины к экваториальной, а длина сплющивание (также называемое сжатостью) ж , - отношение разности экваториально-полярных длин к экваториальной длине:

Первый эксцентриситет (обычно просто эксцентриситет, как указано выше) часто используется вместо сплющивания. [4] Это определяется:

Отношения между эксцентриситетом и уплощением следующие:

Все современные геодезические эллипсоиды определяются большой полуосью плюс малой полуосью (задающей соотношение сторон), уплощением или первым эксцентриситетом. Хотя эти определения математически взаимозаменяемы, реальные вычисления должны терять некоторую точность. Чтобы избежать путаницы, эллипсоидальное определение считает, что его собственные значения являются точными в той форме, которую оно дает.

Приложения

Наиболее распространенные формы распределения плотности протонов и нейтронов в атомное ядро находятся сферический, вытянутой и сжатой сфероидальной формы, где полярная ось считается осью вращения (или направлением вращения угловой момент вектор). Деформированные формы ядер возникают в результате конкуренции между электромагнитный отталкивание между протонами, поверхностное натяжение и квант эффекты оболочки.

Сплюснутые сфероиды

Сплюснутый сфероид - это приблизительная форма вращающегося планеты и другие небесные тела, включая Землю, Сатурн, Юпитер, и быстро вращающаяся звезда Альтаир. Сатурн - самая сжатая планета в Солнечная система, с сплющивание 0,09796. Просвещение ученый Исаак Ньютон, работая с Жан Ришемаятниковые эксперименты и Кристиан Гюйгенстеории для их интерпретации, аргументировал, что Юпитер и Земля сплюснутые сфероиды из-за их центробежная сила. [5] [6] Разнообразные картографические и геодезические системы Земли основаны на справочные эллипсоиды, все они сжатые.

А научная фантастика пример чрезвычайно сжатой планеты Месклин от Хэл Клементроман Миссия гравитации.

Вытянутые сфероиды

Вытянутый сфероид - это приблизительная форма мяча в некоторых видах спорта, например в регби.

Несколько луны Солнечной системы приблизительно имеют форму вытянутых сфероидов, хотя на самом деле они трехосные эллипсоиды. Примеры Сатурнспутники Мимас, Энцелад, и Тетис и Уран' спутниковое Миранда.

В отличие от того, что небесные объекты искажаются в сплющенные сфероиды из-за быстрого вращения, небесные объекты слегка искажаются в вытянутые сфероиды за счет приливные силы когда они вращаются вокруг массивного тела на близкой орбите. Самый яркий пример - спутник Юпитера. Ио, который становится немного более или менее вытянутым по своей орбите из-за небольшого эксцентриситета, вызывая интенсивный вулканизм. Большая ось вытянутого сфероида в этом случае проходит не через полюса спутника, а через две точки на его экваторе, прямо обращенные к основному объекту и от него.

Этот термин также используется для описания формы некоторых туманности такой как Крабовидная туманность. [7] Зоны Френеля, используемые для анализа распространения волн и интерференции в космосе, представляют собой серию концентрических вытянутых сфероидов с главными осями, выровненными вдоль прямой видимости между передатчиком и приемником.

В атомные ядра из актинид и лантаноид элементы имеют форму вытянутых сфероидов. [8] В анатомии почти сфероидные органы, такие как яичко могут быть измерены их длинные и короткие оси. [9]

Многие подводные лодки имеют форму, которую можно описать как вытянутый сфероид. [10]

Динамические свойства

Для сфероида с однородной плотностью момент инерции представляет собой эллипсоид с дополнительной осью симметрии. Учитывая описание сфероида как имеющего большая ось c , и второстепенные оси а и б , моменты инерции вдоль этих главных осей равны C , А , и B . Однако в сфероиде малые оси симметричны. Таким образом, наши инерционные члены по основным осям следующие: [11]

Читайте также: