Электрическое смещение теорема гаусса кратко
Обновлено: 02.07.2024
Поток напряженности электрического поля, проходящий через замкнутую поверхность, пропорционален суммарному электрическому заряду, содержащемуся внутри этой поверхности.
В науке часто бывает, что один и тот же закон можно сформулировать по-разному. По большому счету, от формулировки закона ничего не меняется с точки зрения его действия, однако новая формулировка помогает теоретикам несколько иначе интерпретировать закон и испытать его применительно к новым природным явлениям. Именно такой случай мы и наблюдаем с теоремой Гаусса, которая, по существу, является обобщением закона Кулона, который, в свою очередь, явился обобщением всего, что ученые знали об электростатических зарядах на момент, когда он был сформулирован.
Вообще говоря, в математике, физике и астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса. В 1831 году он вместе со своим молодым коллегой Вильгельмом Вебером (Wilhelm Weber, 1804–1891) занялся изучением электричества и магнетизма и вскоре сформулировал и доказал теорему, названную его именем. Чтобы понять, в чем заключается ее смысл, представьте себе изолированный точечный электрический заряд q. А теперь представьте, что он окружен замкнутой поверхностью. Форма поверхности в теореме не важна — это может быть пусть даже сдутый воздушный шарик. В каждой точке окружающей заряд поверхности, однако, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. Теорема Гаусса как раз и гласит, что суммарный поток напряженности электрического поля, проходящий через окружающую заряд поверхность, пропорционален величине заряда.
Связь между законом Кулона и теоремой Гаусса станет очевидной на простом примере. Предположим, что заряд q окружен сферой радиуса r. На удалении r от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:
E = kq/r 2
И то же самое значение мы получим для любой точки сферы заданного радиуса. Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr 2 ). Иными словами, суммарный поток будет равен:
4πr 2 × kq/r 2 = 4πkq
Это и есть теорема Гаусса.
Интересное следствие из нее получается, если применить эту теорему к сплошному металлу. Представьте себе цельнометаллический предмет и воображаемую замкнутую поверхность внутри него. Полный электрический заряд внутри такой поверхности будет нулевым, поскольку внутри окажется равное число положительных и отрицательных зарядов — протонов атомных ядер и электронов соответственно. Следовательно, поток напряженности электрического поля, проходящий через такую замкнутую поверхность, также будет равен нулю. Поскольку это верно для любой замкнутой поверхности внутри металла, это означает, что внутри металла не существует и не может существовать электрического поля.
Это свойство металлов часто используется экспериментаторами и инженерами-связистами для защиты высокочувствительных приборов от наведенных извне электрических помех. Обычно прибор просто окружается защитным медным экраном. Согласно теореме Гаусса, внешние электрические поля просто не в состоянии проникнуть внутрь такой оболочки и создать помехи работе прибора.
Другое интересное следствие теоремы Гаусса заключается в том, что если в дороге вас застала гроза, самое безопасное для вас — не выходить из машины, поскольку там вы окружены цельнометаллическим экраном. Даже если в ваш автомобиль ударит молния, внутри вам ничего не будет угрожать, поскольку весь разряд пройдет по корпусу и уйдет в землю. Резина, скорее всего, сгорит, зато сами вы останетесь в целости и сохранности.
Для расчета электростатических полей сложных заряженных объектов в диэлектрике, наряду с принципом суперпозиции, используется также теорема Гаусса в следующем виде: Поток вектора электрического смещения D через любую замкнутую поверхность равна алгебраической сумме сторонних зарядов внутри объема, ограниченного данной поверхностью:
где D=eeoE– электрическое смещение, S – замкнутая поверхность, окружающая заряды qi, – поток векторов D через поверхность S.
Относительная диэлектрическая проницаемость среды e показывает, во сколько раз электрическое поле в диэлектрической среде ослабляется по сравнению с вакуумом.
Сторонние заряды это заряды не входящие в состав молекул диэлектрика (хотя и находящиеся в нем). Электрическое смещение Dэто вспомогательный вектор, определяемый только сторонними зарядами и обладающий свойством, что поток его через любую поверхность не терпит разрыва (в отличие от потока вектора Е).
На основе теоремы Гаусса легко, например, получить выражения для
1) напряженности поля, создаваемого бесконечной равномерно заряженной прямой линией или бесконечно длинным цилиндром
где r — расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля, t=q/l - линейная плотность заряда (заряд, приходящийся на единицу длины нити или цилиндра),
2) напряженности поля, создаваемого бесконечной равномерно заряженной плоскостью
Где s= q/S - поверхностная плотность заряда (заряд, приходящийся на единицу площади).
Для расчета электростатических полей сложных заряженных объектов в диэлектрике, наряду с принципом суперпозиции, используется также теорема Гаусса в следующем виде: Поток вектора электрического смещения D через любую замкнутую поверхность равна алгебраической сумме сторонних зарядов внутри объема, ограниченного данной поверхностью:
где D=eeoE– электрическое смещение, S – замкнутая поверхность, окружающая заряды qi, – поток векторов D через поверхность S.
Относительная диэлектрическая проницаемость среды e показывает, во сколько раз электрическое поле в диэлектрической среде ослабляется по сравнению с вакуумом.
Сторонние заряды это заряды не входящие в состав молекул диэлектрика (хотя и находящиеся в нем). Электрическое смещение Dэто вспомогательный вектор, определяемый только сторонними зарядами и обладающий свойством, что поток его через любую поверхность не терпит разрыва (в отличие от потока вектора Е).
На основе теоремы Гаусса легко, например, получить выражения для
1) напряженности поля, создаваемого бесконечной равномерно заряженной прямой линией или бесконечно длинным цилиндром
где r — расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля, t=q/l - линейная плотность заряда (заряд, приходящийся на единицу длины нити или цилиндра),
2) напряженности поля, создаваемого бесконечной равномерно заряженной плоскостью
Где s= q/S - поверхностная плотность заряда (заряд, приходящийся на единицу площади).
Теорема Остроградского-Гаусса или теорема о дивергенции — один из основополагающих законов электродинамики, устанавливающий связь между электрическими зарядами и электрическим полем.
Эта теорема выражает равенство между потоком напряженности электрического поля через замкнутую поверхность и значением заряда \(q\) , расположенного внутри объема этой поверхности.
В отличие от закона Кулона теорема Остроградского-Гаусса позволяет выразить свойства электростатического поля в более общей форме.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Имея заряд \(q\) , окруженный замкнутой поверхностью любой формы, в каждой точке этой поверхности можно наблюдать электрическое поле, спровоцированное этим зарядом. Чтобы найти поток напряженности электрического поля, необходимо перемножить напряженность этого поля и сколь угодно малую единицу окружающей заряд поверхности. А после, зная это, можно рассчитать поток напряженности, который проходится на каждую единицу поверхности.
В этом заключается суть теоремы Остроградского-Гаусса. Ее можно сформулировать как совокупный поток напряженного электрического поля, проходящий через плоскость, окружающую заряд, пропорционален величине заряда.
Теорема активно используется в электродинамике, а для более сложных полевых теорий, существуют ее обобщения и аналоги.
Теорема была выведена двумя учеными независимо друг от друга. Российский математик Михаил Остроградский в 1828 году вывел теорему, применимую для векторного поля любой природы, а то время как его немецкий коллега Карл Гаусс, увлекшись изучением магнетизма и электрических полей, представил миру свою теорему применительно к электростатическому полю.
Михаил Остроградский доказал теорему электростатики через уравнение дифференциальной формы, в то время как Карл Гаусс в 1839 году получил аналогичный результат в интегральной форме.
Физический смысл формулы
Физический смысл формулы сводится к тому, что поток электрической индукции ( \(D\) ) через любую замкнутую поверхность \(S\) пропорционален суммарному заряду, заключенному внутри этой поверхности ( \(q\) ).
Вывод формулы в интегральной форме
Начнем с того, что поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность \(S\) . Обратим внимание на рисунок 1. В данном случае поток вектора напряженности через \(dS\) будет равен:
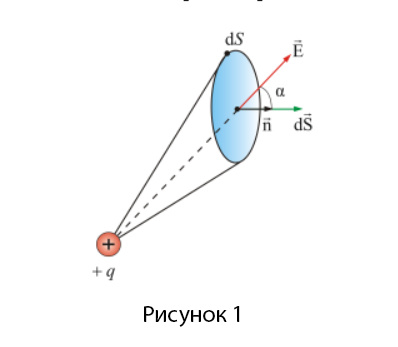
Таким образом, в однородном поле \(\phi_E=ES\) , а в произвольном электрическом поле:
\(\phi_E=\int_SE_ndS=\int_s\overrightarrow Ed\overrightarrow S\)
В этом случае \(d\overrightarrow S=dS\overrightarrow n\) — положение \(dS\) в пространстве задается с помощью вектора \(\overrightarrow n\) . То есть направление вектора \(d\overrightarrow S\) совпадает с направлением \(\overrightarrow n\) .
Теперь попробуем вычислить поток вектора \(\overrightarrow E\) через произвольную замкнутую поверхность \(S\) , которая окружает заряд \(q\) (рисунок 2). Окружим заряд \(q\) сферой \(S_1\) . Центр сферы и центр заряда совпадают, поэтому радиус сферы \(S_1\) равен \(R_1\) .
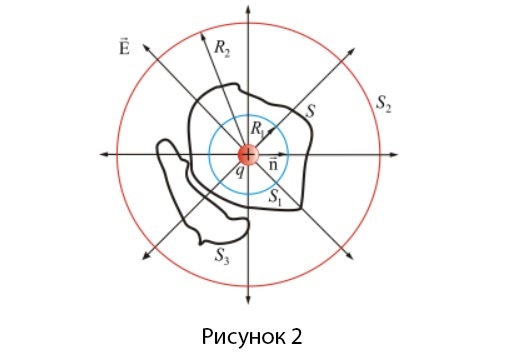
Проекция \(\overrightarrow E\) на направление внешней нормали одинакова на каждой точке поверхности \(S_1\) и вычисляется по формуле:
В таким случае поток через \(S_1\) можно узнать, применив формулу:
Пример
Далее вычислим поток через сферу \(S_2\) , которая имеет радиус \(R_2\) по формуле:
Учитывая непрерывность линии \(\overrightarrow E\) , поток через любую поверхность \(S\) будет равен той же величине:
Формула для нескольких зарядов будет записываться следующим образом:
Вывод формулы в дифференциальной форме
Дифференциальная форма теоремы используется для расчета электростатического поля в случае произвольного пространственного распределения зарядов. В этой форме отражена связь между объемной плотностью заряда \(\rho\) и изменением \(\overrightarrow E\) вокруг этой точки пространства.
Используем теорему Остроградского-Гаусса, в соответствии с которой поток вектора \(\overrightarrow A\) через любую замкнутую поверхность равняется интегралу от его дивергенции по объему, охваченному этой поверхностью:
Пример
В данном случае \(div\overrightarrow A\) в любой точке поля обозначает предел отношения потока вектора \(\overrightarrow A\) через замкнутую поверхность \(S\) , которая охватывает точку \(M\) , к объему \(\triangle V\) части поля, ограничиваемой поверхностью \(S\) , при неограниченном уменьшении \(\triangle V\) :
\(div\overrightarrow A=\lim_\frac1\oint(\overrightarrow Ad\overrightarrow S)\) .
Вернемся к заряду. Предположим, что он распределен в пространстве \(\triangle V\) , а его объемная плотность \( \) , тогда в соответствии с теоремой Остроградского-Гаусса:
\(\oint(\overrightarrow Ed\overrightarrow S)=\frac q\) или же \( \oint(\overrightarrow Ed\overrightarrow S)=\frac< \triangle V>\) .
Если устремить \(\triangle V\) к \(0\) , притягивая его к нужной нам точке, то в этом случае \( \) в этом точке будет стремиться к \(\rho\) , то есть \(\frac< >\rightarrow\frac\rho.\)
Дивергенцией вектора \(\overrightarrow E\) называется величина, которая является пределом отношения \(\oint(\overrightarrow Ed\overrightarrow S)\) к \( \triangle V\) при \(\triangle V\rightarrow0\) . Обозначается это как \(div\overrightarrow E\) и соответствует \(div\overrightarrow E\;=\;\lim_\frac1\oint(\overrightarrow Ed\overrightarrow S\) )
Этим же способом определяется дивергенция любого векторного поля.
Применение формулы
Формула используется для того, чтобы преобразовать объемный интеграл в интеграл по замкнутой поверхности и наоборот.
В матанализе формула теоремы Остроградского-Гаусса используется для вычисления дивергенции, то есть потока векторного поля через поверхность окрестности по внешним направлениям. Принимая во внимание то, что поток векторного поля через замкнутую поверхность \(\delta\) в направлении внешней единичной нормали \(\overline\) равен дивергенции данного поля, вычисленной по телу \(T\) , которое эта поверхность
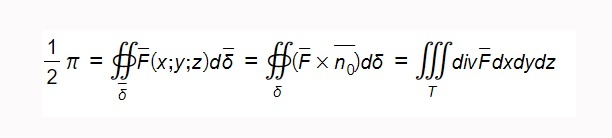
Применение теоремы
Для расчета электростатического поля
Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:
- заряженное тело должно быть окружено простой замкнутой поверхностью;
- вычисление потока вектора напряженности необходимо свести к умножению \(Е\) (или \(E_n\) ) на площадь поверхности \(S\) или часть нее.
Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.
Для плоскости
Рассмотрим применение теоремы для равномерно заряженной плоскости.
Задача
Предположим, что заряд положительный, а плоскость заряжена с постоянной поверхностной плотностью, что выражается в формуле \(\delta=\frac\) . Благодаря симметрии можно сделать вывод, что напряженность в любой точке поля обладает направлением, перпендикулярным плоскости. Из этого же можно сделать вывод, что во всех точках, симметричных плоскости, напряженность поля одинакова, но ее направление противоположно.
Отметим на заряженной плоскости площадь \(\triangle S\) . Определим вокруг площадки замкнутую цилиндрическую поверхность (рисунок 3) так, чтобы ее образующие основания были перпендикулярны плоскости, располагались симметрично, относительно нее и имели величину \(\triangle S\) .
А теперь используем теорему Остроградского-Гаусса: \(\oint_SE_ndS=\frac1^<>>q_1\) . Так как в этом случае \(E_n=0\) в каждой точке, через боковую часть потока не будет. В случае оснований \(E_n=E\) , а исходя из этого совокупный поток через поверхность равен \(2E\triangle S\) .
Посмотрим теперь внутрь поверхности. Там заключен заряд \(\delta\triangle S\) . В соответствии с теоремой Остроградского-Гаусса, должно быть выполнено условие: \(2E\triangle S=\frac\) , из чего следует \(E=\frac\delta\) .
Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.
Для сферической поверхности
Задача
Возьмем поле, которое создает сферическая поверхность с радиусом \(R\) , заряженное с постоянной поверхностной плоскость \(\delta\) . Так как этому полю характерна центральная симметрия, направление вектора \(\overrightarrow E\) в любой точке проходит через центр сферы. Учитывая это, мы знаем, что значение напряженности можно выразить функцией расстояния \(r\) от центра сферы.
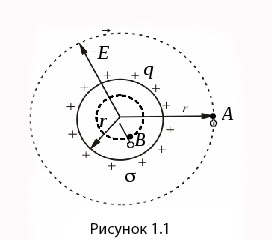
Вычислим напряженность поля. Для начала расчетов проведем через точки на A и B (на рисунке 1.1) сферические поверхности для вычисления потока вектора, проходящего через них. Точка B располагается внутри заряженной поверхности, а ее расстояние от центра составляет \(r\) (при \( r ). Внутри поверхности, которую мы провели через эту точки, заряд содержаться не будет, а, значит, по теореме Остроградского-Гаусса \(\oint_SE_ndS=\frac1^<>>q_1\) , напряженность в этой точки будет равняться нулю.
Теперь обратимся к полю, созданному заряженной сферической поверхностью в точке A, чье расстояние от центра сферы равно \(r\) . Поместим заряженное тело в замкнутое сферическую поверхность радиусом r, проходящей через точку A. В этом случае \(E_n=E(r)\) справедливо для всех точек этой поверхности. Заряд \(q\) , создающий данное поле, пропадает внутри этой поверхности. Таким образом, \(E(r)4\mathrm^2=\frac<\mathrm q><<\mathrm\varepsilon>_0>,\;\mathrm\;\mathrm\;\oint(\overrightarrow<\mathrm E>\mathrm d\overrightarrow<\mathrm S>)=\frac<\mathrm q>_1><<\mathrm\varepsilon>_0>\) . Из этого следует, что напряженность поля в точках, располагающихся на расстоянии \(r>R\) , равняется \(E=\frac1<4\pi\varepsilon_0>\frac q\) .
В диэлектрике
Диэлектрики влияют на электрического поле. Это влияние выражается в ответном действии поляризационных зарядов, которые возникают в поле. Исходя из этого теорему Остроградского-Гаусса для тел в вакууме можно видоизменить, прибавив к свободным зарядам поляризационные, и тогда эту теорему можно применять в диэлектрической среде.
Теорема будет выглядеть так: \(\oint_s\overrightarrow Dd\overrightarrow S=\sum_^Nq_i=Q(2)\)
В этом случае \(\overrightarrow D\) — это вектор электрического смещения, \(q_i\) — это свободные заряды, а \(Q\) — суммарный свободный заряд, находящийся внутри объема, ограниченного поверхностью \(S\) . В вакууме векторы \(\overrightarrow D\) и \(\overrightarrow E\) совпадают.
Для расчета магнитного поля
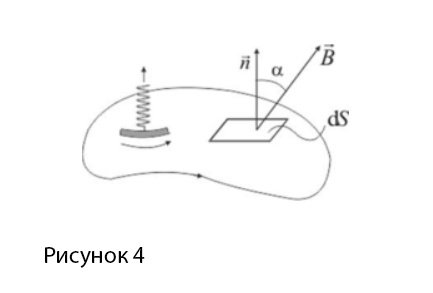
Выделим элементарную бесконечно малую площадку \(dS\) в магнитном поле. Предположим, что она настолько маленькая и плоская, что вектор B можно признать одинаковым по величине и направлению в каждой точке магнитного поля, независимо от того однородно оно или нет.
Тогда поток вектора магнитной индукции сквозь \(dS\) можно определить с помощью выражения \(d\phi=BdS\cos\left(\overrightarrow B\wedge d\overrightarrow S\right)=B_ndS=\overrightarrow Bd\overrightarrow S \) .
В данном случае \(B_n\) равно \(B\cos\left(\alpha\right)\) , где \(\alpha\) это острый угол между направлениями вектора \(В\) и нормалью. \(B_n\) — это проекция вектора магнитной индукции в области нахождения площадки \(dS\) на направление нормали (рисунок 4).
Определение потока магнитной индукции через произвольную поверхность звучит как сумма потоков через элементарные площадки, на которые разбита эта поверхность, и выражается в виде интеграла по этой поверхности:
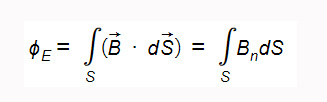
Области применения теоремы
Ценность теоремы Остроградского-Гаусса состоит в формулировке общих свойств электрического поля. Она — один из основных постулатов теории электричества. Поэтому широко применяется в общей и учебной физике и таких ее областях как электромагнетизм, электростатика и механика, с ее помощью решают задачи и изучают векторные (в том числе электромагнитные) поля.
Кроме этого теорема применяется в электродинамике, гидродинамике и математическом анализе.
Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью.
Содержание
Теорема Гаусса для напряжённости электрического поля в вакууме (электростатическая теорема Гаусса)
Общая формулировка: Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
,
,
.
— объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а " width="" height="" />
— оператор набла.
Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.
Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона.
Теорема Гаусса для электрической индукции (электрическое смещение)
Для поля в веществе электростатическая теорема Гаусса может быть записана иначе— через поток вектора
Если же рассматривать теорему для напряжённости поля в веществе, то в качестве заряда Q необходимо брать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика:
,
где ,
>>" width="" height="" />
— Теорема Гаусса для магнитной индукции
Для вычисления электромагнитных полей используются следующие величины:
где dS — бесконечно малый участок поверхности.
где dl — длина бесконечно малого отрезка.
Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии . Поток вектора напряжённости равен " width="" height="" />
. Применив теорему Гаусса, получим:
,
,
Важно отметить, что несмотря на свою универсальность и общность, теорема Гаусса в интегральной форме имеет сравнительно ограниченное применение в силу неудобства вычисления интеграла. Однако в случае симметричной задачи решение её становится гораздо более простым, чем с использованием принципа суперпозиции.
См. также
Литература
- Матвеев А. Н. Электричество и магнетизм: Учебное пособие. — М.: Высшая школа, 1983. — 463 с, ил. и более поздние издания.
- Сивухин Д. В. Общий курс физики, т.3, §§5 — 8, 13, 53.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Теорема Гаусса. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Читайте также:


