Дробные выражения это кратко и понятно

Обновлено: 30.06.2024

В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения

В отличие от них выражения

помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.

Целые и дробные выражения называют рациональными выражениями.

Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.

Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла

при а = 0. При всех остальных значениях а это выражение имеет

смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Выражение вида равно нулю ?

Дробь . Итак, числитель дроби равен нулю при x = 7 и x= -3. Знаменатель данной дроби не равен нулю, если x ≠ -3. Значит, данная дробь равна нулю при x = 7.

2. Основное свойство дроби. Сокращение дробей

Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство

На основании сочетательного и переместительного свойств умножения имеем:

Так как bс ≠ 0, то по определению частного

Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.

Равенство (1) выражает основное свойство рациональной дроби:

если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.

Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.

Пример 1. Приведем дробь к знаменателю

Так как , получим:

если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Дробные выражения

Содержание

Определения дробных выражений

Сегодня на уроке мы с вами приступим к изучению дробных выражений. Для начала начнем с определения, и узнаем, какие именно выражения принято называть дробными.

Дробные выражения – это частное 2-х чисел или выражений, знак деления которого обозначают чертой.

В дробном выражении, то выражение, которое стоит под этой дробной чертой, называют знаменателем.

В дробном выражении его числителями и знаменателями являются какие-либо числа или буквенные выражения.

Вот несколько примеров дробных выражений:

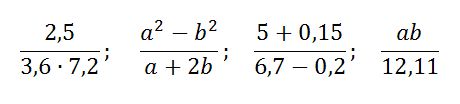
Также как и с обыкновенными дробями, так и с дробными выражениями все действия делаются по одним и тем же правила.

Что такое простая дробь

Прежде чем приступить к изучению дробных выражений и выполнению практических заданий, давайте вспомним, что такое дроби.

Простой дробью называют часть единицы или ее нескольких частей.

Знаменателем простой дроби называют то количество равных частей, на которое делится единица. А числителем простой дроби называют количество взятых частей.

Простая дробь записывается в таком виде:

Из этого следует, что дробь — это число, составленное из целого числа долей единицы.

Историческая справка о математических дробях

Вначале древний человек научился считать предметы, но позднее пришло понимание для измерения длины, времени, площади и вести расчеты при купле-продаже. А в этих случаях не всегда удавалось использовать только натуральные числа, а необходимо было учитывать и какие-то части или доли. Вот так постепенно и появились дроби.

Исторический след исчисления дробей был замечен в использовании многих народов. В Древнем Вавилоне существовала мера в один талант, что составляло 60 мин, одна мина равнялась 60 шекелей. То есть, можно сказать, что в вавилонской системе исчислений применялись шестидесятеричные дроби.

Домашнее задание

Дайте ответы на следующие вопросы:

1. Назовите действия, которые необходимые выполнить, чтобы найти дробь от числа?
2. Какие вы знаете способы нахождения числа по его значению дроби?
3. Сформулируйте правило умножения обыкновенных дробей.
4. Сформулируйте правило деления обыкновенных дробей.
5. Какие выражения принято называть дробными?
6. Чем дробные выражения отличаются от остальных?

Перед вами предоставлены различные виды выражений, выберите из них те, которые являются дробными выражениями.

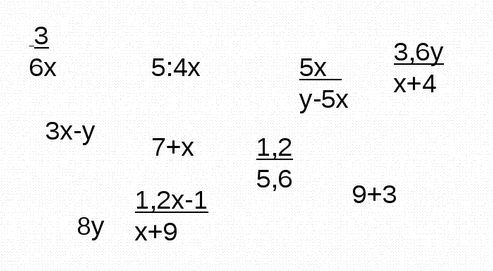
Решите задачи:

1. Таня читает интересную книгу и уже прочла 32 страницы, это составляет 2/3 всей книги. Дайте ответ, сколько в этой книге страниц?

2. Денису четырнадцать лет. Его возраст составляет 2/7 возраста отца. Решите задачу и ответьте, сколько же лет отцу Дениса?

Целыми выражениями называют такие выражения, которые включают в состав числа и переменные, а также действия сложения, вычитания, умножения и деления на число, не равное нулю.

Целыми выражениями, например, являются:

( x 2 – y ) ( x 2 + y )

Дробными выражениями называют такие выражения, которые, кроме действий сложения, вычитания, умножения и деления на число, не равное нулю, включают в себя деление на выражение, содержащее переменные.

Дробными выражениями, например, являются:

3 x – 3 y 2 y + x

x 2 + y 6 + 2 x 2 − y 2

Целые и дробные выражения объединены общим понятием рациональных выражений.

Дробь представляет собой выражение, записанное в виде:

Целые и дробные выражения имеют отличия в некоторых свойствах. Например, целое выражение обладает смыслом при каких-либо значениях переменных, которые включены в его состав. В связи с этим, отсутствуют ограничения по действиям для определения значения целого выражения.

Дробные выражения не во всех случаях имеют смысл. Так, выражение 2 x не имеет смысла при x=0. Выражение 3 x - 3 y y – x не имеет смысла, когда x=y.

Таким образом, дробные выражения имеют смысл только тогда, когда переменные, входящие в их состав, не обращают знаменатель в ноль.

Допустимые значения — такие значения переменных, при которых выражение имеет смысл.

В рамках объяснения темы дробных выражений следует рассмотреть краткое понятие рациональной дроби.

Рациональной дробью называют такую дробь, в которой числитель и знаменатель являются многочленами.

Примеры рациональных дробей:

3 x – 3 y 2 y + x

x 2 + y 6 + 2 x 2 – y 2

Допустимые значения в случае рациональной дроби представляют собой такие значения переменных, при которых знаменатель дроби отличен от нуля.

Алгоритм поиска допустимых значений переменных в дроби:

приравнять знаменатель с переменными к нулю;
решить уравнение, которое получилось;
найденные корни — это значения переменных, обращающих знаменатель в ноль;
исключить данные значения переменных из множества действительных чисел.

Действия с дробями, как упростить со степенями

Основное свойство дроби. При умножении числителя и знаменателя дроби на одинаковое число значение дроби останется неизменным.

Ключевое свойство дроби можно рассмотреть на конкретном примере:

3 5 = 4 · 3 4 · 5 = 12 20 .

Привести дроби к общему знаменателю можно, последовательно выполняя следующие действия:

числитель одной дроби умножить на знаменатель другой дроби;
числитель второй дроби умножить на знаменатель первой дроби;
выполнить замену знаменателей в обеих дробях на их произведение.

Алгоритм сложения дробей:

приведение дробей к общему знаменателю;
сложение полученных числителей;
знаменатель при этом не меняется.

В качестве примера суммируем пару дробей:

3 5 + 1 2 = 6 10 + 5 10 = 11 10 = 1 1 10 .

Алгоритм вычитания дробей:

приведение дробей к общему знаменателю;
вычитание из числителя одной дроби числителя другой дроби;
знаменатель при этом не меняется.

На практике вычитание дробей выполняют таким образом:

3 5 – 1 2 = 6 10 – 5 10 = 1 10 .

Умножение дробей заключается в умножении числителей и умножении знаменателей этих дробей.

Данное действие можно рассмотреть на примере задания:

5 3 · 1 2 = 5 · 1 3 · 2 = 5 6 .

При делении одной дроби на другую необходимо найти произведение числителя первой дроби и знаменателя второй дроби, а также произведение знаменателя первой дроби и числителя второй дроби.

Разберем конкретный пример деления дробей:

5 3 ÷ 1 2 = 5 · 2 3 · 1 = 10 3 = 3 1 3 .

Правила сокращения дробей со степенью:

Если одинаковые числа, которые имеют разные степени, умножают, то данные степени необходимо сложить.
Если одинаковые числа, имеющие разные степени, делят, то данные степени необходимо вычитать.
Возвести степень в степень можно с помощью умножения показателей этих степеней.
Извлечь корень из степени можно путем деления показателя степени на показатель корня.

Разберем записанные правила на наглядном примере:

Используя первое и второе правило из списка, решим задачу:

4 8 × 2 2 ÷ 5 2 × 16 5 = 4 9 ÷ 5 2 × 4 1 0 = 1 ÷ 5 2 × 4 = 1 ÷ 100 = 0 , 01

При решении задач с дробными выражениями полезно знать следующие формулы:

квадрат суммы и квадрат разности: ( a + b ) 2 = a 2 + 2 a b + b 2 ( a – b ) 2 = a 2 – 2 a b + b 2
куб суммы и куб разности: ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 = a 3 + b 3 + 3 a b ( a + b ) ( a – b ) 3 = a 3 – 3 a 2 b + 3 a b 2 – b 3 = a 3 – b 3 – 3 a b ( a – b )

Рассмотрим наглядный пример применения данных формул:

13 3 + 3 · 13 2 · 7 + 3 · 13 · 49 + 7 3 = ( 13 + 7 ) 3 = 20 3 = 8000

Упростить решение дробных выражений также помогут следующие формулы:

разность квадратов: a 2 – b 2 = ( a – b ) ( a + b )
сумма кубов и разность кубов: a 3 + b 3 = ( a + b ) ( a 2 - a b + b 2 ) a 3 – b 3 = ( a – b ) ( a 2 + a b + b 2 )

В качестве примера упростим выражение:

7 6 - 2 6 7 4 + 14 2 + 16 = ( 7 2 – 2 2 ) ( 7 4 + 7 2 · 2 2 + 2 4 ) 7 4 + ( 7 · 2 ) 2 + 2 4 = 7 2 – 2 2 = 45

Примеры с решением и ответами

Определить значение выражения:

5 · ( 3 - x 2 ) ( x - 3 ) ( x + 3 )

Условием являются такие значения переменной х, при которых выражение обладает смыслом.

5 · ( 3 - x 2 ) ( x - 3 ) ( x + 3 ) = 5 · ( 3 - x 2 ) x 2 - ( 3 ) 2 = 5 · ( 3 - x 2 ) x 2 - 3 = - 5 · ( x 2 - 3 ) x 2 - 3 = - 5

Дано выражение, значение которого требуется найти:

( x 3 + y 3 ) · ( x - y ) x 2 - x y + y 2 - x 2 + y 2 .

( x 3 + y 3 ) · ( x - y ) x 2 - x y + y 2 - x 2 + y 2 = ( x + y ) · ( x 2 - x y + y 2 ) · ( x - y ) x 2 - x y + y 2 - x 2 + y 2 = = ( x + y ) · ( x - y ) - x 2 + y 2 = x 2 - y 2 - x 2 + y 2 = 0

Определить значение выражения:

11 u + 9 v + 15 2

3 - 19 u - 6 v 5 u + 4 + 6 v = 5 и 6 v + 5 u + 4 ≠ 0 .

Если 6 v + 5 u + 4 ≠ 0 , получим, что следующие выражения равносильны:

3 - 19 u - 6 v 5 u + 4 + 6 v = 5

3 - 19 u - 6 v = 5 ( 5 u + 6 v + 4 )

44u + 36v + 30 = 13

Данное выражение является равносильным:

4 ( 11 u + 9 v + 7 , 5 ) = 4 · 3 , 25 .

11 u + 9 v + 15 2 = 3 , 25 .

В данном случае:

q ( t ) = 7 t - 9 t 7 t - 9 t

Нужно определить значение этого выражения с такими t, при которых выражение имеет смысл.

q ( - t ) = - 7 t + 9 t - 7 t + 9 t = q ( t ) ,

q 1 t = 7 t - 9 t 7 t - 9 t = q ( t )

В таком случае, при аналогичных t:

q ( 1 t ) q ( - t ) = q ( t ) q ( t ) = 1 .

Дано выражение, значение которого требуется вычислить:

( 2 a + 3 b ) 2 - 2 a 2 - 3 b 2 : ( 24 a b )

Так как a b ≠ 0 , получим:

( 2 a + 3 b ) 2 - 2 a 2 - 3 b 2 : ( 24 a b ) = 2 a 2 + 2 6 a b + 3 b 2 - 2 a 2 - 3 b 2 : ( 24 a b ) = 2 6 a b 2 6 a b = 1 .

Определить значение следующего выражения с такими х, при которых оно имеет смысл:

1 x · - π + π - x 2 π - x

С помощью формулы разности квадратов выполним преобразования:

1 x · - π + π - x 2 π - x = 1 x · - π + ( π - x ) ( π + x ) π - x

1 x · ( - π + π + x ) = 1 .

Определить значение следующего выражения с такими m, при которых данное выражение не лишено смысла:

( sin ( 1 ) m 2 - 4 ) · 1 sin ( 1 ) m - 2 - 1 sin ( 1 ) m + 2

Воспользуемся формулой разности квадратов:

( sin ( 1 ) m 2 - 4 ) · 1 sin ( 1 ) m - 2 - 1 sin ( 1 ) m + 2 = = ( sin ( 1 ) m - 2 ) ( sin ( 1 ) m + 2 ) · 1 sin ( 1 ) m - 2 - 1 sin ( 1 ) m + 2 = [ 4 pt ] = ( sin ( 1 ) m - 2 ) ( sin ( 1 ) m + 2 ) sin ( 1 ) m - 2 - ( sin ( 1 ) m - 2 ) ( sin ( 1 ) m + 2 ) sin ( 1 ) m + 2 = [ 4 pt ] = sin ( 1 ) m + 2 - ( sin ( 1 ) m - 2 ) = 4

Определить g(1) при следующем условии:

F ( 2 x - 1 ) = 4 x - 7 и F ( g ( x ) ) = x 3 .

F ( a ) = 4 · a + 1 2 - 7 = 2 a - 5

F ( g ( x ) ) = 2 g ( x ) - 5 = x 3

g ( x ) = 1 2 x 3 + 5

g ( 1 ) = 1 2 1 + 5 = 3 .

Дано выражение, значение которого требуется определить:

6 x 2 + 5 x - 1 + x + 4 x + 1 ÷ 3 x - 2 + 3 x + 1

В первую очередь обратимся к выражениям, заключенным в скобках. Попробуем привести их к общему знаменателю и выполнить деление полученных дробей:

( 6 x 2 + 5 x - 1 ) ( x + 1 ) + x + 4 x + 1 ÷ ( 3 x - 2 ) ( x + 1 ) + 3 x + 1 =

6 x 3 + 11 x 2 + 5 x + 3 x + 1 ÷ 3 x 2 + x + 1 x + 1 =

6 x 3 + 11 x 2 + 5 x + 3 x + 1 · x + 1 3 x 2 + x + 1 =

6 x 3 + 11 x 2 + 5 x + 3 3 x 2 + x + 1

6 x 3 + 11 x 2 + 5 x + 3 3 x 2 + x + 1 ¯ 6 x 3 + 2 x 2 + 2 x ¯ 2 x + 3 9 x 2 + 3 x + 3 9 x 2 + 3 x + 3 ¯ 0

Заметим, что получился нулевой остаток. Таким образом, допустимо записать числитель дроби, как:

6 x 3 + 11 x 2 + 5 x + 3 = ( 2 x + 3 ) ( 3 x 2 + x + 1 )

6 x 3 + 11 x 2 + 5 x + 3 3 x 2 + x + 1 = ( 2 x + 3 ) ( 3 x 2 + x + 1 ) 3 x 2 + x + 1 = 2 x + 3

Найдем значение выражения, если x=2017:

2 · 2017 + 3 = 4037

Найти значение следующего выражения:

y 2 - 4 x y - x 2 ( 3 x + y ) ( x + y ) + 10 · x y - 3 x 2 y 2 - 9 x 2 - 2

При расчетах следует учитывать, что:

Преобразуем выражение при условии, что ( 3 x + y ) ( x + y ) ≠ 0 и y 2 - 9 x 2 ≠ 0 :

y 2 - 4 x y - x 2 ( 3 x + y ) ( x + y ) + 10 · x ( y - 3 x ) ( y - 3 x ) ( y + 3 x ) - 2 =

В этом уроке мы вспомним понятия числового выражения, буквенного выражения. Сформируем представления о дробном выражении. Введем понятие дробного выражения. Рассмотрим упражнения по нахождению значения дробного выражения.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Дробные выражения"

Мы с вами уже знакомы с разными видами выражений.

Например,

Числовые выражения – это выражения, которые состоят из чисел, арифметических действий и скобок.

Буквенные выражения – это выражения, которые состоят из букв, чисел, арифметических действий и скобок.

Дроби – это и обыкновенные дроби, и десятичные дроби, и смешанные числа.

А значит и с помощью них тоже можно составлять некоторые выражения. Мы уже знаем, что черта дроби и знак деления – это одно и то же математическое действие. Поэтому черту дроби можно понимать, как знак деления.

Значит и в выражении знак деления можно заменить чертой дроби.

Выполнив последовательно все действия, получим значение данного выражения:

Определение

Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой,— знаменателем дробного выражения. Числителем и знаменателем дробного выражения могут быть как любые числа, так и числовые или буквенные выражения.

С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями.

Давайте рассмотрим некоторые дробные выражения. На экране представлены 4 примера дробных выражений. Найдём их значения.

Задание

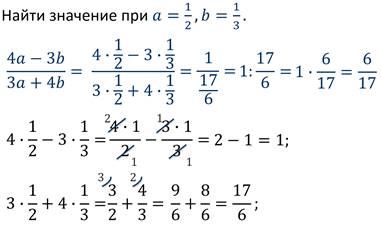
Итак, сегодня на уроке, мы узнали, что частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Чтобы найти значение дробного выражения, нужно найти по отдельности значения его числителя и знаменателя и затем первый результат разделить на второй.

Читайте также: