Диаграмма эйлера венна кратко

Обновлено: 05.07.2024

Диаграмма Венна — это графический способ выражения связи между разными элементами, событиями или тем, что надо между собой сравнить.

Что такое Venn diagram?

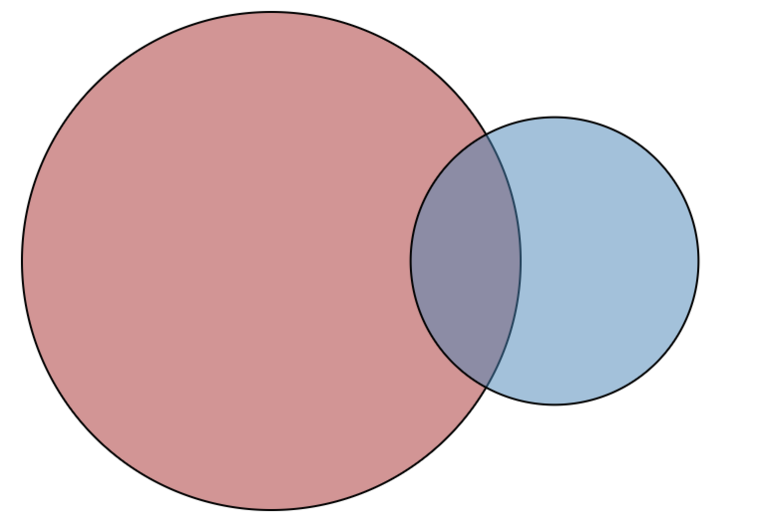
Диаграмма Венна — это графический способ выразить связи между разными элементами, событиями и чем угодно, что надо между собой сравнить. Понятия изображают в кругах.

Когда нужны диаграммы Венна?

К venn diagram обращаются для сравнения данных, если: * эти самые данные слишком сложно понять; * если не так просто выявить взаимосвязи между данными.

Как создать venn diagram?

Считаем группы объектов, которые нужно сравнить между собой. По их количеству рисуем круги, они должны частично перекрывать друг друга.

Venn Diagram

Диаграмма Венна — это графический способ выразить связи между разными элементами, событиями и чем угодно, что надо между собой сравнить. Понятия изображают в кругах. Место пересечения этих кругов показывает их общность.

На примерах все станет понятнее. Например, в вашей компании работает 30 человек. 20 из них топят за Путина. 15 — за Лукашенко. На первый взгляд история невозможная, ведь тут уже получается 35 сотрудников. Но если изобразим все в кругах, то будет видно, что как минимум 5 человек (их может быть и больше) поддерживают сразу двух президентов одновременно.

Возьмем еще один, менее радикальный, пример. Допустим, у нас есть две группы объектов: световые устройства и энергосберегающие технологии. Помещаем их в разные круги, которые пересекаются. Что находится в этой области пересечения? В ней будут объекты, которые относятся и к первой, и ко второй группе. То есть это энергосберегающие лампочки или другие источники света.

Когда нужны диаграммы Венна

К venn diagram обращаются для сравнения данных, если:

эти самые данные слишком сложно понять;
если не так просто выявить взаимосвязи между данными.

Визуализация информации помогает быстрее осмыслить и проанализировать сравниваемые объекты, найти между ними пересечения. Поэтому диаграммы Венна часто используют в презентациях для наглядности.

Также диаграммы Венна применяют:

в математике;
в логике;
в менеджменте;
и других прикладных областях, где нужно сопоставлять какие–либо множества и устанавливать между ними связи.

Как создать venn diagram

Нарисовать диаграмму Венна довольно просто. Сделать это можно за четыре шага.

Считаем группы объектов, которые нужно сравнить между собой. По их количеству рисуем круги.
Рисуем первый круг. Он должен быть достаточно большим.
Затем рисуем второй круг такого же размера. Он должен частично перекрывать первый. Внутри области пересечения оставьте место. Там будем отмечать объекты, которые сравниваем.
Называем каждую группу объектов и подписываем круги.

Из чего состоит диаграмма Венна

Область, где круги накладываются друг на друга, называется пересечением.
Когда все круги вместе — это называют объединением.
Части круга, которые не пересекаются, то есть имеют больше различий, чем сходств, называют симметрической разностью.
Область одного круга, которая не попадает в пересечение, это — относительное дополнение.
Любая область за кругами и за пределами множества называется абсолютное дополнение.
Область за кругами — это универсальное множество.

История создания venn diagram

Диаграммы в виде круга начали использовать еще в 13 веке. Однако популярными и всемирно известными их сделал английский логик Джон Венн в 1880 году.

Джона Венна вдохновил математик Леонард Эйлер. Он использовал диаграммы с кругами, но они у него не пересекались. Венн же предложил их пересекать и обосновал свое решение.

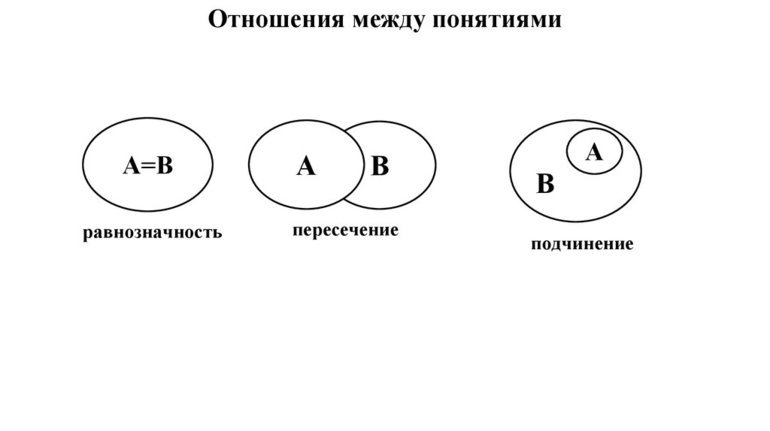
Круги Эйлера (другое название — диаграммы Венна) — это геометрическая схема, которую можно применять для наглядного отображения отношений между множествами. Диаграммы разработал известный математик и механик, чьим именем и назван метод. Учёный считал, что его подход облегчает размышления человека.

Множества в математике

Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:

конечное, например, множество стран;
бесконечное — множество звёзд во вселенной;
пустое — множество острых углов в прямоугольнике.

Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.

дополнение ¯A в калькуляторе имеет вид A';
пересечение A∩B представлено как A intersection B;
объединение А⋃B обозначено A union B;
симметрическая разность A∆B — symmetric difference of A and B;
Относительное дополнение A\B — A\B.

Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.

Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.

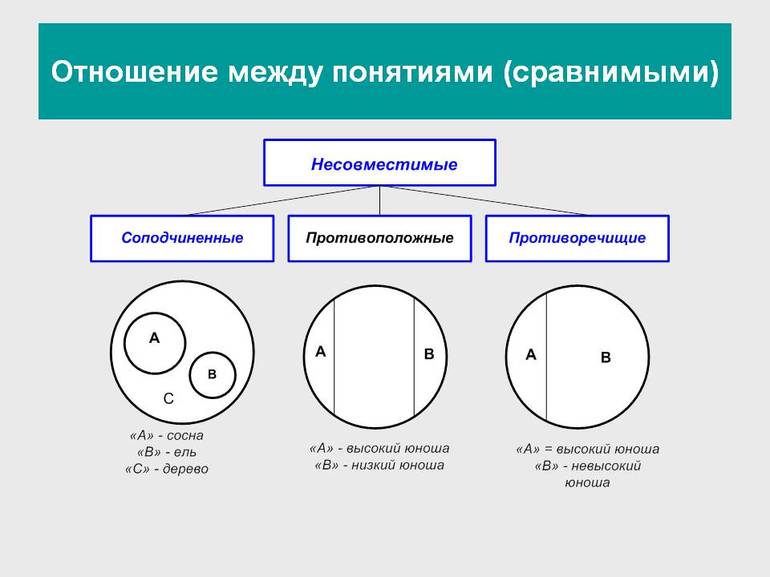
Отношения между понятиями

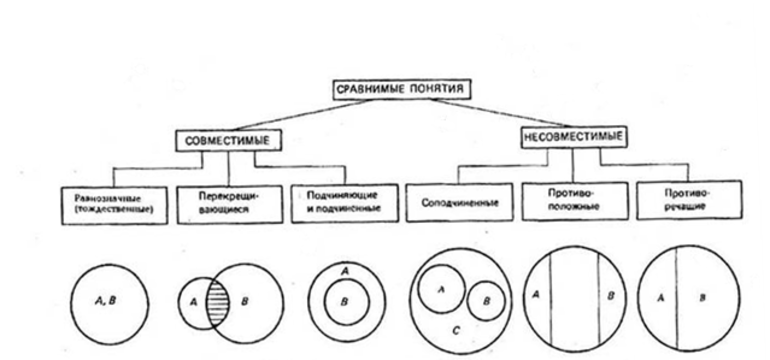
Рисунок 1

Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:

равнозначные (тождественные);
перекрещивающиеся;
подчиняющие и подчинённые.

Несовместимыми называют понятия, не имеющие общих элементов:

соподчинённые;
противоположные;
противоречащие.

Решение задач, примеры

Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.

Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?

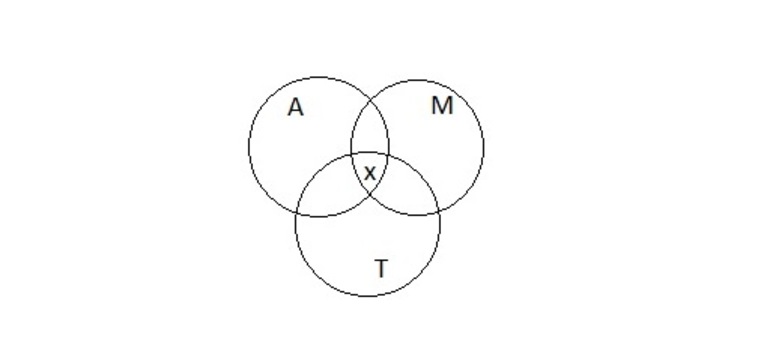
Рисунок 2

Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.

Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…

Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…

Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).

54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.

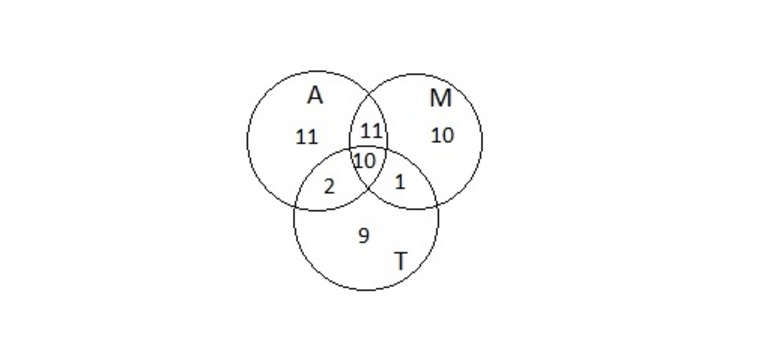
Рисунок 3

Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?

Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.

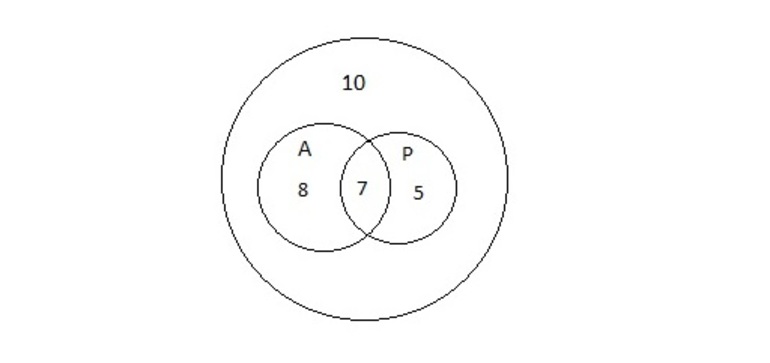
Рисунок 4

(. ) - задание скобок; A - отрицание, инверсия, дополнение (NOT); ∪ - дизъюнкция, объединение (OR); ∩ - конъюнкция, пересечение (AND); = - эквивалентность (тождество) (↔); → - импликация (следование); \ - относительное дополнение (разность); △ - симметрическая разность.

Для вложенного отрицания необходимо использовать знак ! . Например, A ∪ B = !(A ∪ B ) или A ∪ B = A ∪ !B
Чтобы доказать равенство, например, (A\B)\C∩B = (A\C)\(B\C) , необходимо отдельно ввести (A\B)\C∩B и (A\C)\(B\C) , а затем сравнить их результаты. ►
Далее
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение ).

Множества изображаются в виде кругов или эллипсов, помещенных в прямоугольник (универсум).

Универсальное множество (универсум) U - множество, содержащее все элементы рассматриваемых подмножеств и элементы, не входящие в них.
Пустое множество Ø - множество, не содержащее ни одного элемента рассматриваемых подмножеств.
Количество пересечений (областей) n определяется по формуле: n=2 N ,
где N - количество множеств.

Рисование кругов Эйлера

С помощью этого инструмента можно будет вручную создавать круги Венна с индивидуальным оформлением. Чтобы заштриховать требуемую область, нажмите на кнопку Заштриховать область , а затем выберите номер области. Для снятия штриховки, повторно нажмите на этот же номер. ►

Алгоритм построения диаграмм Эйлера-Венна

Определяют количество подмножеств ( А , В , С , D ).
На диаграмме строят пересекающиеся множества, включенных в универсум.
Выделяют области, количество которых равно количеству пересечений.

Диаграммы Эйлера-Венна для одного множества А

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 1 = 2 строк (областей)
Примеры
Универсум U=, А=
A = , A ∩ A = ∩ = <> = Ø

Диаграммы Эйлера-Венна для двух множеств А и В

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 2 = 4 строк (областей)
Примеры
Универсум U=, А=, В=
A∪B = ∪ =

Диаграммы Эйлера-Венна для трех множеств А , В , С

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 3 = 8 строк (областей)
Примеры
Универсум U=, А=, В=, C=
B\C ∪ A = \ ∪ = ∪ =

Диаграммы Эйлера-Венна для четырех множеств А , В , С , D

На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 4 = 16 строк (областей)
Примеры
Универсум U=
А=
В=
C=
D=

Логические операции

Список литературы

Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.

Добавить текст

Все права защищены и охраняются законом. Copyright © ООО Новый семестр 2006-2021
Этот сайт использует cookie для сбора статистики по посещаемости. Отключить их можно, изменив настройки используемого Вами браузера. Задать вопрос или оставить комментарий Помощь в решении Поиск

Поиск

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus .
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Круги́ Э́йлера [1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2 n комбинаций n свойств, то есть конечную булеву алгебру. При n = 3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы. [2]

Примечания

См. также

Ссылки

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Диаграммы Эйлера—Венна" в других словарях:

Диаграммы Венна — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия

ДИАГРАММЫ ВЕННА — ДИАГРАММЫ ВEHHА графический способ задания и анализа логико математических теорий и их формул. Строятся путем разбиения части плоскости на ячейки (подмножества) замкнутыми контурами (кривьми Жордана). В ячейках представляется информация,… … Философская энциклопедия

Круги Эйлера — Пример кругов Эйлера. Буквами обозначены, например, свойства: живое существо, человек, неживая вещь Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения … Википедия

Диаграмма Эйлера — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия

Диаграмма Венна — Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные) Диаграмма Венна … Википедия

Логические диаграммы — графический (геометрический, точнее топологический) аппарат математической логики (См. Логика). Идея Л. д. была известна ещё в средние века, развивалась затем Г. В. Лейбницем, но впервые достаточно подробно и обоснованно была изложена Л.… … Большая советская энциклопедия

Формула включений-исключений — (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия

Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия

Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия

Читайте также: