Через две пересекающиеся прямые проходит плоскость и притом только одна доказательство кратко
Обновлено: 05.07.2024

У аксиом стереометрии есть несколько очень нужных следствий, которые упрощают решения задач и доказательства теорем. На данном уроке мы рассмотрим эти следствия и решим несколько задач, при решении которых будем использовать сами аксиомы стереометрии и следствия из них.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Некоторые следствия из аксиом стереометрии"
На прошлом уроке мы с вами познакомились с аксиомами стереометрии. Давайте еще раз повторим их.
Первая аксиома звучит так: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Вторая аксиома звучит так: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Третья аксиома звучит так: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Сегодня на уроке мы сформулируем и докажем некоторые следствия из этих аксиом. По аналогии с аксиомами следствия мы будем обозначать заглавной буквой С с нижним индексом.
Итак, первое следствие звучит так: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Докажем это. Рассмотрим прямую a и не лежащую на ней точку B. Нам необходимо доказать, что через прямую a и точку B проходит плоскость. Отметим на прямой a две точки C и D. Точки B, C, D не лежат на одной прямой, поэтому согласно первой аксиоме, (а именно, тому что через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна) через эти точки проходит некоторая плоскость α. Поскольку точки C и D прямой a лежат в плоскости, то по второй аксиоме (если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости) вся прямая a лежит в плоскости α.

Теперь давайте докажем единственность этой плоскости. Любая плоскость, которая проходит через прямую a и точку B проходит через точки B, C, D. То есть она совпадает с плоскостью α, поскольку по первой аксиоме, плоскость, которая проходит через три точки, не лежащие на одной прямой – единственная.
Теперь давайте сформулируем и докажем второе следствие.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Рассмотрим прямые a и b, которые пересекаются в точке А. Тогда нам необходимо доказать, что через эти прямые проходит плоскость, и притом только одна.
Отметим на прямой b точку B, не совпадающую с точкой А. Тогда из первого следствия, через прямую a и точку B можно провести плоскость α. Так как точки А и B прямой b лежат в плоскости α, то по второй аксиоме мы получим, что вся прямая b лежит в плоскости α. Поскольку через прямую и не лежащую на ней точку можно провести только одну плоскость, то значит, любая плоскость, проходящая через прямые a и b совпадает с плоскостью α.

Таким образом, наша теорема доказана.
Решим несколько задач.
Задача. Две прямые пересекаются в точке . Доказать, что все прямые, которые пересекают данные прямые и не проходят через точку , лежат в одной плоскости.
По второму следствию из аксиом стереометрии через две пересекающиеся прямые проходит плоскость, и притом только одна. Значит, через данные прямые проведем плоскость альфа.

Проведем прямую, которая будет пересекать прямые, но не проходит через точку B. Эта прямая с каждой из данных прямых имеет по одной общей точке. Эти точки принадлежат построенной плоскости, поскольку прямые принадлежат этой плоскости. Получаем, что две точки прямой принадлежат плоскости, значит, по второй аксиоме, вся прямая лежит в этой же плоскости. Поскольку прямую мы проводили произвольно, то, очевидно, что каждая из прямых, которые будут пересекать исходные прямые будет лежать в этой же плоскости, что и требовалось доказать.
Задача. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
Первое утверждение неверно, так как окружность и плоскость имеют две общие точки, если они пересекаются. То есть окружность не лежит в плоскости, а только пересекает ее.

Перейдем ко второму утверждению. По первой аксиоме через три точки, не лежащих на одной прямой можно провести плоскость и притом только одну. Точки окружности не могут лежать на одной прямой, поэтому проведем через них плоскость. Очевидно, что эти точки лежат в плоскости окружности, но поскольку аксиома говорит о том, что такая плоскость единственная, значит, окружность будет принадлежать этой плоскости. То есть второе утверждение верно.

Задача. Пусть точки не лежат на одной прямой. Отметим на прямой точку , а на прямой – точку . Доказать, что точка прямой лежит в плоскости .

По первой аксиоме через точки А, B, C проведем плоскость α. Так как прямая АB лежит в плоскости α, значит, точка D лежит в плоскости α. Аналогично, поскольку прямая АC лежит в плоскости α, то и точка Е лежит в плоскости α. Получаем, что две точки прямой DE лежат в плоскости α. Применим вторую аксиому и получим, что вся прямая DE лежит в плоскости α. Тогда точка F прямой DE тоже лежит в плоскости α. Что и требовалось доказать.
Задача. Пусть стороны и треугольника лежат в плоскости . Доказать, что и медиана лежит в плоскости .

Поскольку стороны AB и АC лежат в плоскости α, значит, точки B и C лежат в этой плоскости, то есть, по второй аксиоме, сторона BC тоже лежит в этой плоскости. Точка M лежит на прямой BC, значит, она лежит в плоскости α, что и требовалось доказать.
Подведем итоги урока. Итак, сегодня на уроке мы повторили аксиомы стереометрии, сформулировали и доказали некоторые следствия из аксиом и рассмотрели задачи, на использование аксиом и следствий из них.
Теорема. Через две пересекающиеся прямые проходит единственная плоскость.
Доказательство.
Пусть имеются две пересекающиеся прямые р n q, n D — их общая точка.
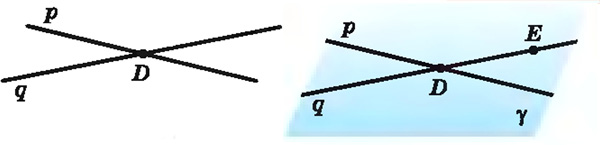
Выберем на прямой q какую-либо точку Е, отличную от точки D. В соответствии с теоремой (Через прямую и точку вне ее проходит единственная плоскость) через прямую р и точку Е проходит единственная плоскость γ. Плоскость γ проходит и через прямую q, так как две точки D и Е прямой q принадлежат плоскости γ.
Допустим, что через прямые р и q проходит еще одна плоскость σ. Тогда плоскость σ проходит через точку Е. Но через эту точку и прямую р, в соответствии с теоремой, проходит единственная плоскость. Значит, плоскость σ совпадает с плоскостью γ. Таким образом, через пересекающиеся прямые р и q проходит единственная плоскость.
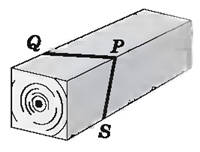
Теорема находит свое применение на практике. Если столяру нужно распилить брусок под определенным углом, он, чтобы наметить плоскость распила, проводит в двух смежных гранях бруска пересекающиеся прямые PQ и PS.

На этом уроке мы рассмотрим некоторые следствия из аксиом. Рассмотрим и докажем теорему о том, что через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Рассмотрим и докажем теорему о том, что через две пересекающиеся прямые проходит плоскость, и притом только одна. Далее с помощью аксиом и двух теорем-следствий мы решим несколько задач.

Отметим на прямой b какую-нибудь точку N, отличную от точки M, и рассмотрим плоскость, через точку N и прямую а. Так как две точки прямой b лежат в плоскости, то по аксиоме А2 плоскость проходит через прямую b. Итак плоскость проходит через прямые а и b. единственность такой плоскости следует из того, что любая плоскость, проходит через прямые а и b, проходит через точку N. Следовательно, она совпадает с плоскостью, поскольку через точку N и прямую а проходит только одна плоскость
Читайте также:

