Быстрое преобразование фурье кратко

Обновлено: 02.07.2024

Основная задача, которая решается при помощи быстрого преобразования Фурье (Fast Fourier Transform, FFT) — это умножение многочленов за время $O(n \log n)$.

Тривиально (по определению) многочлены степеней $m$ и $n$ умножаются за время $O(nm)$. Долгое время считалось, что быстрее это сделать невозможно, А.Н. Колмогоров даже принимал попытки доказать нижнюю границу, пока в 1960 году А. Карацуба не придумал способ умножать многочлены степени $n$ за время $O(n^<\log_<2>3>)$.

Как известно, многочлен степени строго меньше $n$ однозначно определяется своими значениями в $n$ (вообще говоря комплексных) точках. Действительно, если есть два различных многочлена с одинаковыми значениями в $n$ точках, то их разность имеет $n$ комплексных корней, причём она является ненулевым многочленом степени строго меньше $n$, что противоречит основной теореме алгебры. С другой стороны, интерполяционный многочлен Лагранжа в явном виде предъявляет многочлен степени строго меньше $n$ по значениям в $n$ точках.

Таким образом, многочлены можно хранить не в виде вектора коэффициентов, а в виде набора значений в некоторых точках. Над многочленами в таком виде очень удобно производить арифметические операции, в том числе умножать их за время $O(n)$ (нужно просто перемножить значения в соответствующих точках). С другой стороны, непонятно, как считать значения в других точках, да и знать сами коэффициенты бывает полезно. А воостанавливать коэффициенты по значениям в некотором наборе точек сложно, тот же интерполяционный многочлен Лагранжа вычисляется за время $O(n^2)$. Да и многочлены нам обычно задаются в форме вектора коэффициентов, получить значеня в $n$ произвольных точках вряд ли можно быстрее, чем за $O(n^2)$.

Хитрость FFT в том, что точки, в которых считаются значения многочлена, выбираются отнюдь не произвольным образом.

Описание

Итак, FFT преобразует вектор $\langle a_, a_, \ldots, a_ \rangle$ в вектор $\langle b_, b_, \ldots, b_ \rangle$, где $b_ = \sum_^ a_ e^<2 \pi i \frac>$, $n=2^$, иначе говоря, преобразует вектор коэффициентов многочлена степени $n-1$ в набор его значений в точках $\omega_ = e^<2 \pi i \frac>$.

Тут сразу возникает два вопроса:

1. Что делать с многочленами других степеней?
2. Почему именно эти точки?

С первым вопросом всё просто: нужно дополнять коэффициенты нулями до ближайшей степени двойки.

Со вторым же вопросом дело чуть хитрее. $\omega_$ - это комплексные корни из $1$ $n$-й степени, то есть $\omega_^n = 1$. У них есть замечательные свойства: $\omega_ = \omega_^$, $\omega_ \omega_ = \omega_$.

Разделяй и властвуй

$A_$ и $A_$ - многочлены степени $\frac = 2^$, к ним можно применить FFT и получить набор значений в точках $e^> = e^> = \omega_$.

$A(\omega_) = A_(\omega_^) + \omega_ A_(\omega_^) = A_(\omega_) + \omega_ A_(\omega_)$. Таким образом, зная FFT для $A_$ и $A_$, можно вычислить FFT для $A$.

Осталось определить базу рекурсии — $n=1$. Для этого нужно посчитать значение константного многочлена $A=a_$ в точке $\omega_ = 1$. Это значение, очевидно, равно $a_$.

Таким образом, алгоритм работает за время $T(n) = 2 T(\frac) + O(n)$. По мастер-теореме $T(n) = O(n \log n)$.

Обратное преобразование

Хорошо, мы научились по многочлену вычислять его значение в $n$ особых точках за $O(n \log n)$, потом мы можем перемножить значения и получить FFT от произведения многочленов. Но мы пока не умеем восстанавливать многочлен по его FFT.

Можно рассмотреть FFT как линейное преобразование:

Возведём матрицу преобразования в квадрат: $R_ = \sum_^ \omega_^ \omega_^ = \sum_^ \omega_ = \sum_^ \omega_^$

Если $\omega_ = 1$, то $R_ = n$. В противном случае можно посчитать сумму геометрической прогрессии и получить $0$.

Таким образом, обратное преобразование выглядит следующим образом:

1. Применить прямое преобразование
2. Разделить все элементы на $n$
3. Развернуть массив без первого элемента

Оптимизации

В общем-то, это всё; однако данная реализация работает не очень быстро и потребляет $O(n \log n)$ памяти.

Что мы глобально делаем:

1. Переставляем коэффициенты
2. Делаем рекурсивные запуски
3. Склеиваем результаты

Если один раз в самом начале применить все перестановки индексов, то можно будет сразу двигаться от более глубоких уровней рекурсии в начало.

Как переставляются индексы: в левую часть идут чётные индексы, в правую — нечётные, потом к каждой из половин рекурсивно примерняется то же правило. Если рассмотреть битовую запись числа, то мы сначала сортируем по младшему биту, потом “отрезаем” его и делаем дальше то же самое. Нетрудно догадаться, что мы на самом деле сортируем индексы по реверснутой битовой записи; строгое доказательство проводится мат.индукцией по номеру уровня.

Реверснутую битовую запись всех чисел от $0$ до $2^-1$ можно предподсчитать с помощью ДП, воспользовавшись следующей идеей: $rev(mask) = rev(mask \oplus 2^) \oplus 2^$.

Также можно заранее предподсчитать комплексные корни из $1$. Тут есть тонкий момент: синусы и косинусы весьма медленные, в то время как если считать $\omega_ = \omega \omega_$, то может набежать большая погрешность. Можно использовать промежуточные варианты, например, честно посчитать первые $2^>$ значений, а также значения по индексам, кратным $2^>$, а все остальные корни разложить в произведение двух уже посчитанных.

Наконец, можно уменьшить количество умножений комплексных чисел. Вспомним, что

Их можно считать одновременно, это уменьшит количество умножений вдвое.

Умножение многочленов

Размер применяемого FFT должен быть строго больше, чем степень произведения многочленов.

В задачах часто многочлены имеют целочисленные коэффициенты, причём неотрицательные. Понятно, что при таких условиях коэффициенты у произведения будут тоже целыми и неотрицательными.

С таким способом округления следует быть осторожным, он верен только для неотрицательных чисел. Если коэффициенты многочлена могут быть отрицательными, следует округлять аккуратно:

Также нужно помнить, что double имеет точность около $15$ знаков, поэтому расчитывать на точное умножение многочленов можно только если коэффициенты произведения не превосходят $10^$, а лучше и ещё меньше.

Разные мелочи

При реализации я пользовался встроенным классом complex . Чтобы его использовать, нужно подключить заголовочный файл complex .

Разумеется, можно использовать не только complex , но и complex или complex double> . Первый вариант действительно может помочь уменьшить время работы и объём потребляемой памяти.

Удивительно, но написание своего класса Complex также может уменьшить время работы.

В общем случае нам нужно 3 вызова FFT, чтобы перемножить два многочлена. Существуют методы, позволяющие проводить 2 FFT одновременно. Но если у нас есть два набора из $n$ и $m$ многочленов, и мы хотим посчитать попарные произведения, то для этого достаточно $n + m + nm$ вызовов FFT.

Операции по модулю

Часто в задачах просят посчитать что-то по модулю некоторого числа. Это же может относиться и к произведению многочленов. Конечно, в таком случае у нас все коэффициенты целые неотрицательные. Однако если модуль порядка $10^$, то коэффициенты произведения могут получиться порядка $10^$, что нельзя не то что точно сохранить в double , а даже сохранить в long long , чтобы потом взять остаток по модулю. Что же делать?

“Хороший” модуль

Почему мы вообще использовали комплексные числа, если все коэффициенты исходных многочленов были действительными? Дело в том, что нам нужно было $n$ разных корней из $1$, чего действительные числа предоставить не могут. Если бы только был какой-то другой объект с такими свойствами…

Как известно из теории чисел, ненулевые остатки по модулю простого числа $P$ образуют циклическую группу порядка $P-1$ по умножению. Пусть $P-1$ делится на достаточно большую степень двойки, то есть $P-1 = nz$ для некоторого целого $z$. Тогда в этой группе тоже есть $n$ разных корней из $1$ степени $n$, и они тоже обладают всеми необходимыми нам свойствами.

Таким образом, мы можем выполнять все операции по модулю $P$, а комплексные корни из $1$ нужно заменить на корни из $1$ по модулю.

Таким образом, если нам повезло, то всё хорошо. Но нужно понимать, что в рамках соревнований “повезло” — это значит авторы задачи сделали так, чтобы нам повезло. Поэтому если вы видите в задаче “необычный модуль”, это может быть сильным намёком на то, что в задаче требуется FFT. С другой стороны, давать такую огромную подсказку — это нежелательно для авторов. Так или иначе, коротенький список часто встречающихся “необычных модулей”, подходящих для написания FFT по модулю: $7340033 = 7 \cdot 2^ + 1$, $998244353 = 119 \cdot 2^ + 1$.

Любой модуль

Тут есть два принципиально разных подхода:

Несколько хороших модулей + Китайская теорема об остатках

Название говорит само за себя. Можно незавсимо выполнить умножение по 3 разным хорошим модулям, а потом узнать искомые коэффициенты при помощи КТО.

Разбить на многочлены с меньшими коэффициентами

Выберем $Q \approx 1000$. Запишем

Коэффициенты многочленов $A_(x)B_(x)$ будут порядка $nQ^2 \le 10^$.

Применение

Понятно, что FFT используется для умножения многочленов, так что это будет скорее описание применений умножения многочленов.

Умножение длинных чисел

Длинные числа умножаются как многочлены (коэффициенты — это цифры), только потом нужно сделать переносы. Однако лучше разбивать цифры на группы по три, то есть рассматривать число в системе счисления по основанию $1000$, — таким образом степени многочленов уменьшаются в три раза.

Вычисление скалярных произведений

Есть массив $A$ длины $n$ и массив $B$ длины $m$ ($m \le n$). Нужно посчитать скалярные произведения $B$ со всеми подотрезками $A$ длины $m$.

Перевернём $B$ и умножим с $A$ как многочлены. Несложно понять, что после переворота скалярное произведение превращается в свёртку. Коэффициенты с $(m-1)$-го по $(n-1)$-й — это ответы.

Нечёткий поиск

Есть строчки $S$ и $P$ над алфавитом $\Sigma$. Для каждой подстроки $S$ длины $ | P | $ найти расстояние Хэмминга (количество позиций, в которых строки отличаются).

Будем считать не расстояние Хэмминга, а $ | P | $ - расстояние, то есть количество совпадающих позиций. Переберём символ из $\Sigma$. В каждой строчке заменим все вхождения данного символа на $1$, а всех остальных — на $0$. Мы свели задачу к предыдущей.

Сложность — $O( | \Sigma | n \log n)$.

Используя эту задачу, можно решать задачи вида “Найдите все вхождения с не более чем $k$ ошибками”.

Все суммы

Есть два множества чисел $A$ и $B$, все числа целые от $0$ до $n$. Выдать все числа из $\lbrace x = a + b \mid a \in A, b \in B \rbrace$.

Динамическое программирование

Иногда в ДП переход выглядит как свёртка, и его можно ускорить при помощи FFT.

Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.

Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.

Здесь и пригодится знание преобразования Фурье.

Что такое звук в математическом смысле?

Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.

Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.

Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.

Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.

Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?

Геометрическая интерпретация преобразования Фурье

Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.

В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.

1. Наматываем сигнал

Давайте начнём с самого простого случая. Рассмотрим гармонический сигнал, совершающий 3 колебания в секунду (f₀ = 3с -1 ):

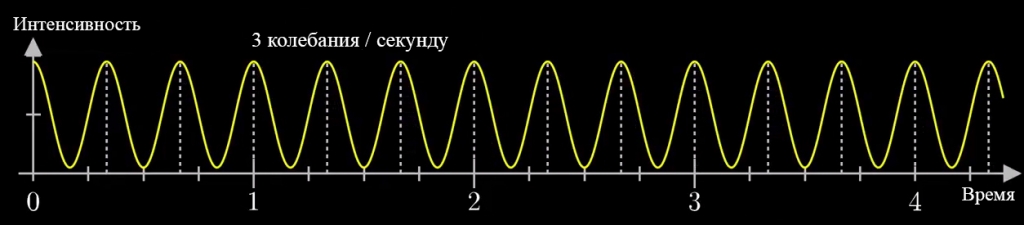
Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.

Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения f_В = 0.5 об/с.

Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная "намотка" сливается с началом координат, а при приближении к максимумам – отклоняется.

Пока выглядит не особо информативно, не так ли?

А теперь увеличим частоты намотки.

Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения f_В = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.

2. Ищем центр масс

Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).

Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.

Мы видим два пика: в точках f_В = 0 об/с и f_В = 3 об/с. На основании такого поведения центра масс уже можно судить о частоте исходного сигнала (он колеблется с f = 3с -1 ).

Тогда что означает всплеск на низких частотах?

3. Анализируем влияние смещения

Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.

При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.

Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.

Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.

Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.

Таким образом, на графике остался только один резкий скачок.

Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.

4. Выделяем частоты полигармонического сигнала

Мы наблюдаем два пика в точках f_В = 2 об/с и f_В = 3 об/с, что соответствует частотному составу исходной суммы.

Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.

Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.

Вывод преобразования Фурье

В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:

Геометрически это соотношение означает, что при любом φ точка e iφ на комплексной плоскости лежит на единичной окружности.

Построим радиус-вектор e iφ при разных значениях φ.

При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.

Тогда намотка сигнала g(t) описывается как g(t)e -2π ift .

Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:

Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:

где t₁ и t₂ – границы интервала, на котором рассматривается сигнал.

Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.

Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.

Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.

Применение преобразования Фурье для фильтрации

Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.

При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.

После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.

На прошлой лекции мы изучили, что такое дискретное преобразование Фурье (ДПФ), изучили его свойства, подводные камни, способы улучшения результатов, а также частотно-временное преобразование Фурье.

Вспомним выражение для ДПФ:

Из него видно, что для расчёта -точечного ДПФ требуется вычислений с комплексными числами. Получается ресурсозатратно, особенно если мы имеем дело с большим количеством отсчётов.

Учёным не нравилось делать много вычислений, и несколько человек (существуют разные мнения, кто был первым) предложили алгоритмы, позволяющие вычислять ДПФ, производя меньшее количество математических операций. Называются такие алгоритмы Быстрое преобразование Фурье (БПФ).

Хочу сразу отметить, что БПФ возвращает абсолютно такие же результаты, что и ДПФ, использует в основе ту же формулу, только позволяет достичь этих результатов гораздо быстрее.

В рамках данной лекции рассмотрим два самых распространённых алгоритма БПФ — с прореживанием по времени и с прореживанием по частоте.

Итак, выше мы уже отметили, что для -точечного ДПФ требуется операций комплексного умножения и сложения. А что, если разделить исходный сигнал на два длиной отсчётов каждый? Тогда получается, что для вычисления ДПФ от одной из половин потребуется математических операций. Или для двух половин (если не считать процедуру разделения и объединения). Получается, эффективность вычислений возрастает в два раза! Но это ещё не предел. Мы можем делить наш сигнал до тех пор, пока не получим набор из сигналов, состоящих из двух отсчётов:

Разбиение сигнала до N=2

, тогда:

:

отличается от второй половины только знаком:

Если произведение выходит за диапазон от 0 до 7, мы также увидим повторяемость этих значений. Например, при , а :

Следовательно, в процессе ДПФ вычисление одних и тех же значений повторяется несколько раз. Наша задача — оптимизировать процесс так, чтобы избежать выполнение повторяющихся операций.

Давайте разделим сигнал на отсчёты с чётными и нечётными номерами, как показано на рисунке:

Прореживание сигнала по времени

Эта операция называется прореживание по времени. Математически это можно записать следующим образом:

Тогда, выражение (3) принимает вид:

Это был расчёт ДПФ для первых отсчётов. Теперь запишем подобное выражение для второй половины отсчётов:

Давайте теперь по очереди разбираться со всеми множителями:

, то выражение (8) принимает вид:

Рассмотрим следующий множитель:

то выражение (10) можно упростить:

Подставим результаты из (9) и (12) в уравнение (7) и получим:

Для простоты восприятия сделаем две замены:

Тогда, с учётом (14) и (15), сгруппируем уравнения (6) и (13):

Полученное выражение (16) называется графом “бабочка”. Почему? Это станет ясно, если посмотреть на его графическое представление:

Граф “бабочка” для БПФ с прореживанием по времени

Данное выражение лежит в основе БПФ с прореживанием по времени.

Таким образом, берём анализируемый сигнал и продолжаем разбивать его на сигналы, состоящие из чётных и нечётных индексов до тех пор, пока не получим набор сигналов из двух отсчётов. На рисунке ниже показан пример такого разбиения для сигнала из восьми отсчётов.

Алгоритм БПФ с прореживанием по времени для N=8

Для вычисления ДПФ такого сигнала требуется 3 стадии разбиения. На первом этапе получаем набор из четырёх ДПФ от сигналов из двух отсчётов:

Далее, на основе полученных результатов формируется два ДПФ для сигналов, состоящих из четырёх отсчётов:

И на последнем этапе формируются итоговые результаты восьмиточечного ДПФ:

Если количество отсчётов исходного сигнала , где — целое положительное число, то его разбиение на сигналы, состоящие из чётных и нечётных индексов вплоть до последнего уровня можно сделать легко и за одну итерацию с помощью двоично-инверсной перестановки.

Для этого записываем индексы всех отсчётов в двоичной системе счисления, при этом должны быть записаны все бит индекса, включая ведущие нули. Затем зеркально отображаем код каждого из этих двоичных чисел и записываем полученные результаты обратно в десятичную систему счисления. Готово! Если расставить элементы исходного массива в соответствии с полученными индексами, мы получим подряд идущие пары отсчётов для двухточечного ДПФ. Пример, как это работает для сигнала из восьми отсчётов, представлен в таблице:

Номер до перестановки	Двоичное	Двоично-инверсная перестановка	Десятичное
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

Можете сравнить с рисунком выше, действительно совпадает. Именно поэтому, рассматриваемые нами алгоритмы также называются БПФ по основанию два. У них есть одно небольшое ограничение — количество отсчётов анализируемого сигнала должно быть равно степени двойки (например, 16, 32, 64, 128, 256 и т.д.). “Но как же быть, если, скажем, в моём сигнале всего 200 отсчётов?” — спросите вы. Ничего страшного, нужно просто дополнить сигнал нулевыми отсчётами, пока его длина не станет равна ближайшей степени двойки.

Как вы догадались из названия раздела, прореживать можно не только время, но ещё и частоту. Граф “бабочка” для БПФ с прореживанием по частоте показан на рисунке:

Граф “бабочка” для БПФ с прореживанием по частоте

Подробно рассматривать данный алгоритм не будем, просто примем его как данность. Пример БПФ с прореживанием по частоте для сигнала, состоящего из 8 отсчётов показан ниже:

Алгоритм БПФ с прореживанием по частоте для N=8

Прореживание (двоично-инверсная перестановка) в данном случае производится уже после вычисления ДПФ, т.е. по частотным отсчётам, отсюда и такое название.

По количеству операций умножения данный алгоритм схож с алгоритмом прореживания по времени, поэтому эффективность их схожая. Какой метод выбрать — решать вам.

В вышеупомянутых “бабочках” есть множитель . Он называется поворотным коэффициентом. На нижнем уровне БПФ, когда имеем дело с двумя отсчётами, требуется всего один поворотный коэффициент . Умножение на единицу считается тривиальной операцией, откуда следует, что на первом уровне не требуется ни одной операции умножения, только сложение и вычитание.

На втором уровне у нас получается два поворотных коэффициента и . Умножение на также делается просто: нужно поменять местами действительную и мнимую часть, а также инвертировать знак мнимой части. На этом уровне также не требуется операций умножения.

На следующем уровне требуется четыре поворотных коэффициента , , и , их значения мы рассчитывали в начале нашей статьи.

Давайте проиллюстрируем на графике все упомянутые выше поворотные коэффициенты (и даже немного больше):

Из графика видно, что на каждом следующем уровне количество поворотных коэффициентов увеличивается в два раза, при этом половина из них совпадает с поворотными коэффициентам предыдущего уровня.

Когда БПФ используется для решения каких-либо задач в устройствах цифровой обработки сигналов, количество отсчётов анализируемого сигнала как правило заранее известно и скорее всего не будет меняться в процессе работы устройства. Поэтому, чтобы не тратить время на вычисление , их заранее рассчитанные значения для заданного количества отсчётов и всех уровней разбиения записывают в памяти в виде таблицы констант, которые в дальнейшем будут использоваться для умножения в графах “бабочка”.

вычислений с комплексными числам.

Чтобы наглядно продемонстрировать эффективность алгоритма, давайте взглянем на таблицу:

Кол-во отсчётов, N	Количество вычислений с комплексными числами		Эффективность
	ДПФ	БПФ
256	65 536	1 024	64:1
512	262 144	2 304	114:1
1024	1 048 576	5 120	205:1
2048	4 194 304	11 264	373:1
4096	16 777 216	24 576	683:1

Особенно заметен прирост эффективности с увеличением количества отсчётов.

Рассмотрим такую распространённую операцию как умножение двух целых чисел. Квадратичный алгоритм — умножения в столбик — все знают со школы. Долгое время предполагалось, что ничего быстрее придумать нельзя.

Первым эту гипотезу опроверг Анатолий Карацуба. Его алгоритм сводит умножение двух \(n\) -значных чисел к трём умножениям \(\frac\) -значных чисел, что даёт оценку времени работы

\[ T(n)=3T\left(\dfrac n 2\right)+O(n)=O\left(n^<\log_2 3>\right)\approx O(n^) \]

Чтобы перейти к алгоритму с лучшей оценкой, нам нужно сначала установить несколько фактов о многочленах.

Умножение многочленов

Обратим внимание на то, что любое число можно представить многочленом:

\[ \begin A(x) &= a_0 + a_1\cdot x + a_2 \cdot x^2 + \dots + a_n \cdot x^n \\ &= a_0 + a_1\cdot 2 + a_2 \cdot 2^2 + \dots + a_n \cdot 2^n \end \]

Основание x при этом может быть выбрано произвольно.

Прямая формула для произведения многочленов имеет вид

\[ \left(\sum_^n a_i x^i\right)\cdot\left(\sum_^m b_j x^j\right)=\sum_^x^k\sum_a_i b_j \]

Её подсчёт требует \(O(n^2)\) операций, что нас не устраивает. Подойдём к этой задаче с другой стороны.

Интерполяция

Теорема. Пусть есть набор различных точек \(x_0, x_1, \dots, x_\) . Многочлен степени \(n\) однозначно задаётся своими значениями в этих точках. (Коэффициентов у этого многочлена столько же, сколько и точек — прим. К. О.)

Доказательство будет конструктивным — можно явным образом задать многочлен, который принимает заданные значения \(y_0, y_1, \ldots, y_n\) в этих точках:

Корректность. Проверим, что в точке \(x_i\) значение действительно будет равно \(y\) :

Для \(i\) -го слагаемого внутреннее произведение будет равно единице, если вместо \(x\) подставить \(x_i\) : в этом случае просто перемножается \((n-1)\) единица. Эта единица помножится на \(y_i\) и войдёт в сумму.

Для всех остальных слагаемых произведение занулится: один из множетелей будет равен \((x_i - x_i)\) .

Уникальность. Предположим, есть два подходящих многочлена степени \(n\) — \(A(x)\) и \(B(x)\) . Рассмотрим их разность. В точках \(x_i\) значение получившегося многочлена \(A(x) - B(x)\) будет равняться нулю. Если так, то точки \(x_i\) должны являться его корнями, и тогда разность можно записать так:

\[ A(x) - B(x) = \alpha \prod_^n (x-x_i) \]

для какого-то числа \(\alpha\) . Тут мы получаем противоречие: если раскрыть это произведение, то получится многочлен степени \(n+1\) , который нельзя получить разностью двух многочленов степени \(n\) .

Этот многочлен называется интерполяционным многочленом Лагранжа, а сама задача проведения многочлена через точки — интерполяцией.

Примечание. На практике интерполяцию решают методом Гаусса: её можно свести к решению линейного уравнения \(aX = y\) , где \(X\) это матрица следующего вида:

\[ \begin 1 & x_0 & x_0^2 & \ldots & x_0^n \\ 1 & x_1 & x_1^2 & \ldots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^n \\ \end \]

Важный факт: многочлен можно однозначно задать не только своими коэффициентами, но также корнями и значениями хотя бы в \((n+1)\) -ой точке.

Умножение через интерполяцию

Что происходит со значениями многочлена-произведения \(A(x) B(x)\) в конкретной точке \(x_i\) ? Оно просто становится равным \(A(x_i) B(x_i)\) .

Основная идея алгоритма: если мы знаем значения в каких-то различных \(n + m\) точках для обоих многочленов \(A\) и \(B\) , то, попарно перемножив их, мы за \(O(n + m)\) операций можем получить значения в тех же точках для многочлена \(A(x) B(x)\) — а с их помощью можно интерполяцией получить исходный многочлен и решить задачу.

Если притвориться, что evaluate и interpolate работают за линейное время, то умножение тоже будет работать за линейное время.

К сожалению, непосредственное вычисление значений требует \(O(n^2)\) операций, а интерполяция — как методом Гаусса, так и через символьное вычисление многочлена Лагранжа — и того больше, \(O(n^3)\) .

Но что, если бы мы могли вычислять значения в точках и делать интерполяцию быстрее?

Комплексные числа

Определение. Комплексные числа — это числа вида \(a + bi\) , где \(a\) и \(b\) это обычные вещественные числа, а \(i\) это так называемая мнимая единица: это число, для которого выполняется равенство \(i^2 = -1\) .

С комплексными числами можно работать почти так же, как с действительными. Они даже удобнее: все квадратные корни всегда извлекаются, все корни многочленов всегда находятся.

Комплексная плоскость

Комплексные числа удобно изображать на плоскости в виде вектора \((a, b)\) и считать через них всякую геометрию.

Модулем комплексного числа называется действительное число \(r = \sqrt\) . Геометрически, это длина вектора \((a, b)\) .

Аргументом комплексного числа называется действительное число \(\phi \in (-\pi, \pi]\) , для которого выполнено \(\tan \phi = \frac\) . Геометрически, это значение угла между \((a, 0)\) и \((a, b)\) . Для нуля — вектора \((0, 0)\) — аргумент не определён.

Таким образом комплексное число можно представить в полярных координатах:

\[ a+bi = r ( \cos \phi + i \sin \phi ) \]

Подобное представление удобно по следующей причине: чтобы перемножить два комплексных числа, нужно перемножить их модули и сложить аргументы.

Упражнение. Докажите это.

Формула эйлера

Определим число Эйлера \(e\) как число со следующим свойством:

\[ e^ = \cos \phi + i \sin \phi \]

Просто введём такую нотацию для выражения \(\cos \phi + i \sin \phi\) . Не надо думать, почему это так.

Геометрически, все такие точки живут на единичном круге:

Такая нотация удобна, потому что можно обращаться с \(e^\) как с обычной экспонентой. Пусть мы, например, хотим перемножить два числа на единичном круге с аргументами \(a\) и \(b\) . Тогда это можно записать так:

\[ (\cos a + i \sin a) \cdot (\cos b + i \sin b) = e^ \]

Упражнение. Проверьте это: раскройте скобки и проделайте немного алгебры.

Корни из единицы

У комплексных чисел есть много других замечательных свойств, но нам для алгоритма на самом деле потребуется только следующее:

А именно, это будут числа вида:

На комплексной плоскости эти числа располагаются на единичном круге на равном расстоянии друг от друга:

Все 9 комплексных корней степени 9 из единицы

Первый корень \(w_1\) (точнее второй — единицу считаем нулевым корнем) называют образующим корнем степени \(n\) из единицы. Возведение его в нулевую, первую, вторую и так далее степени порождает последовательность нужных корней единицы, при этом на \(n\) -ном элементе последовательность зацикливается:

Будем обозначать \(w_1\) как просто \(w\) .

Упражнение. Докажите, что других корней быть не может.

Дискретное преобразование Фурье

Дискретным преобразованием Фурье называется вычисление значений многочлена в комплексных корнях из единицы:

Обратным дискретным преобразованием Фурье называется, как можно догадаться, обратная операция — интерполяция коэффициентов \(x_i\) по значениям \(X_i\) .

Почему эта формула верна? При вычислении ПФ мы практически применяем матрицу к вектору:

\[ \begin w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^1 & w^2 & w^3 & \dots & w^ \\ w^0 & w^2 & w^4 & w^6 & \dots & w^ \\ w^0 & w^3 & w^6 & w^9 & \dots & w^ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^ & w^ & w^ & \dots & w^1 \end\begin a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_ \end = \begin y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_ \end \]

То есть преобразование Фурье — это просто линейная операция над вектором: \(W a = y\) . Значит, обратное преобразование можно записать так: \(a = W^y\) .

Как будет выглядеть эта \(W^\) ? Автор не будет пытаться изображать логичный способ рассуждений о её получении и сразу её приведёт:

\[ W^ = \dfrac 1 n\begin w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^ & w^ & w^ & \dots & w^ \\ w^0 & w^ & w^ & w^ & \dots & w^ \\ w^0 & w^ & w^ & w^ & \dots & w^ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^ & w^ & w^ & \dots & w^ \end \]

Проверим, что при перемножении \(W\) и \(W^\) действительно получается единичная матрица:

Значение \(i\) -того диагонального элемента будет равно \(\frac \sum_k w^ w^ = \frac n = 1\) .

Значение любого недиагонального ( \(i \neq j\) ) элемента \((i, j)\) будет равно \(\frac \sum_k w^ w^ = \frac \sum_k w^k w^ = \frac \sum_k w^k = 0\) , потому что все комплексные корни суммируются в ноль, то есть \(\sum w^k = 0\) (см. картинку — там всё симметрично).

Внимательный читатель заметит симметричность форм \(W\) и \(W^\) , а также формул для прямого и обратного преобразования. На самом деле, эта симметрия нам сильно упростит жизнь: для обратного преобразования Фурье можно использовать тот же алгоритм, только вместо \(w^k\) использовать \(w^\) , а в конце результат поделить на \(n\) .

Зачем это надо?

Напомним, что мы изначально хотели перемножать многочлены следующим алгоритмом:

Посчитаем значения в \(n+m\) каких-нибудь точках обоих многочленов

Перемножим эти значения за \(O(n+m)\) .

Интерполяцией получим многочлен-произведение.

В общем случае быстро посчитать интерполяцию и даже просто посчитать значения в точках нельзя, но для корней единицы — можно. Если научиться быстро считать значения в корнях и интерполировать (прямое и обратное преобразование Фурье), но мы можно решить исходную задачу.

Схема Кули-Тьюки

Представим многочлен в виде \(P(x)=A(x^2)+xB(x^2)\) , где \(A(x)\) состоит из коэффициентов при чётных степенях \(x\) , а \(B(x)\) — из коэффициентов при нечётных.

Пусть \(n = 2k\) . Тогда заметим, что

Зная это, исходную формулу для значения многочлена в точке \(w^t\) можно записать так:

Ключевое замечание: корней вида \(w^\) в два раза меньше, потому что \(w^n = w^0\) , и можно сказать, что.

У нас по сути в два раза меньше корней (но они так же равномерно распределены на единичной окружности) и в два раза меньше коэффициентов — мы только что успешно уменьшили нашу задачу в два раз.

Заметим, что если \(w\) это образующий корень степени \(n = 2k\) из единицы, то \(w^2\) будет образующим корнем степени \(k\) , то есть в рекурсию мы можем просто передать другое значение образующего корня.

Таким образом, мы свели преобразование размера \(n\) к двум преобразованиям размера \(\dfrac n 2\) . Следовательно, общее время вычислений составит

\[ T(n)=2T\left(\dfrac n 2\right)+O(n)=O(n\log n) \]

Заметим, что предположение о делимости \(n\) на \(2\) имело существенную роль. Значит, \(n\) должно быть чётным на каждом уровне, кроме последнего, из чего следует, что \(n\) должно быть степенью двойки.

Реализация

Приведём код, вычисляющий БПФ по схеме Кули-Тьюки:

Как обсуждалось выше, обратное преобразование Фурье удобно выразить через прямое:

Теперь мы умеем перемножать два многочлена за \(O(n \log n)\) :

Примечание. Приведённый выше код, являясь корректным и имея асимптотику \(O(n\log n)\) , едва ли пригоден для использования на реальных контестах. Он имеет большую константу и далеко не так численно устойчивый, чем оптимальные варианты написания быстрого преобразования Фурье. Мы его приводим, потому что он относительно простой.

Читателю рекомендуется самостоятельно задуматься о том, как можно улучшить время работы и точность вычислений. Из наиболее важных недостатков:

внутри преобразования не должно происходить выделений памяти

работать желательно с указателями, а не векторами

корни из единицы должны быть посчитаны наперёд

Следует избавиться от операций взятия остатка по модулю

Вместо вычисления преобразования с \(w^\) можно вычислить преобразование с \(w\) , а затем развернуть элементы массива со второго по последний.

Здесь приведена одна из условно пригодных реализаций.

Но главная проблема в численной стабильности — мы нарушили первое правило действительных чисел. Однако, от неё можно избавиться.

Number-theoretic transform

\[ m = 998244353 = 7 \cdot 17 \cdot 2^ + 1 \]

Это число простое, и при этом является ровно на единицу больше числа, делящегося на большую степень двойки. При \(n=2^23\) подходящим \(g\) является число \(31\) . Заметим, что, как и для комплексных чисел, если для некоторого \(n=2^k\) первообразный корень - \(g\) , то для \(n=2^\) первообразным корнем будет \(g^2 (mod m)\) . Таким образом, для \(m=998244353\) и \(n=2^k\) первообразный корень будет равен \(g=31 \cdot 2^ (mod m)\) .

Реализация практически не отличается.

Применения

Даны две бинарные строки \(a\) и \(b\) . Нужно найти такой циклический сдвиг строки \(b\) , что количество совпадающих соответствующих символов с \(a\) станет максимально.

Сперва научимся для каждого циклического сдвига \(i\) второй строки считать количество совпадающих единиц \(c_i\) . Это можно сделать за \(O(n^2)\) множеством разных способов, мы рассмотрим следующий: рассмотрим каждую единицу во втором числе, пусть она стоит на \(j\) -й позиции; для каждого \(l\) от \(0\) до \(n-1\) , если \(a_l\) равно 1, то прибавим один к \(c_\) (при этом \(i-j\) берётся по модулю \(n\) ). Такой алгоритм верный, потому что по сути мы перебираем пары единиц, которые могут совпадать, и прибавляем +1 к количеству совпадающих единиц для соответствующего циклического сдвига. И тут мы можем заметить очень важную вещь: если перемножить числа, соответствующие \(a\) и \(b\) , в столбик и не переносить разряды при сложении, то мы получим как раз массив \(c\) (с одним нюансом: его длина может быть больше \(n\) , тогда нам нужно для всех \(i \geq n\) прибавить \(c_i\) к \(c_\) )! А перемножать длинные числа мы уже научились: это легко сделать при помощи БПФ. Таким образом, мы научились искать число совпадающих единиц; заметим, что мы можем инвертировать биты в строках и применить эквивалентный алгоритм, получив в итоге количества совпадающих нулей. Сложим соответствующие элементы в двух массивах и найдём индекс максимального. Также очень часто в задачах на FFT требуется не явно перемножить два полинома, а посчитать свёртку двух векторов. Прямой свёрткой векторов \(a\) длины \(n\) и \(b\) длины \(m\) называется вектор \(s\) длины \(n+m-1\) такой, что \(s_k = \Sigma_^ a_i \cdot b_ (\forall k \in [0;n+m-2])\) (при этом считается, что несуществующие элементы равны нулю). Круговой (циклической) свёрткой векторов \(a\) и \(b\) длины \(n\) называется вектор \(s\) длины \(n\) такой, что \(s_k = \Sigma_^ a_i \cdot b_ (\forall k \in [0; n-1])\) (при этом \(\) берётся по модулю \(n\) ). Оказывается, что линейную свёртку можно считать через круговую: для этого дополним нулями оба вектора до одинаковой длины \(n+m-1\) . Это очень легко доказать: если для некоторого \(k\) \(i \geq k+1\) , то либо \(a_i\) , либо \(b_\) будут равны нулю. Если расписать выражение для прямого преобразования Фурье круговой свёртки и перенести множетили, то можно получить, что круговая свёртка равна вектору произведений многочленов с коэффициентами \(a\) и \(b\) в точках \(0,1,\dots n-1\) . Возможно, когда-нибудь я это распишу.

Читайте также:

  
• Опишите проявления народной культуры кратко
  
• Быт казаков на кубани кратко
  
• Ядерная стратегия россии кратко
  
• Тройственная сущность человека кратко
  
• Теория торсионных полей кратко