Алгоритм флойда уоршелла кратко
Обновлено: 02.07.2024
Алгоритм Флойда-Уоршелла [1] [2] [3] предназначен для решения задачи поиска всех кратчайших путей на графе. Для заданного ориентированного взвешенного графа алгоритм находит кратчайшие расстояния между всеми парами вершин за время [math]O(n^3)[/math] . Алгоритм применим к графам с произвольными, в том числе с отрицательными, весами. Таким образом, он является более общим в сравнении с алгоритмом Дейкстры, который не работает с отрицательными весами ребер. Также алгоритм распознаёт наличие отрицательных циклов.
1.2 Математическое описание алгоритма
Имеем граф [math]G=(V,E)[/math] , в котором каждая вершина пронумерована от [math]1[/math] до [math]|V|[/math] . Сформируем матрицу смежности [math]D[/math] . Эта матрица имеет размер [math]|V|*|V|[/math] и каждому ее элементу [math]D_[/math] присвоен вес ребра, соединяющего вершину [math]i[/math] с вершиной [math]j[/math] . Заметим, что в силу ориентированности графа [math]G[/math] матрица [math]D[/math] может быть несимметрична.
По мере выполнения алгоритма данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины [math]i[/math] в вершину [math]j[/math] .
Полагаем диагональные элементы [math]D_[/math] равными нулю, а недиагональные элементы, соответствующие не инцидентным вершинам (не имеющим общего ребра), положим равными бесконечности или числу, заведомо большему возможного расстояния между ребрами.
Ключевая часть алгоритма состоит из трех циклов:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если [math]+D_ \lt D_>[/math] , то [math]
1.3 Вычислительное ядро алгоритма
Основной операцией алгоритма является релаксация элементов матрицы смежности: если [math]+D_ \lt D_>[/math] , то производится присваивание [math]
1.4 Макроструктура алгоритма
Ключевая часть алгоритма состоит из трех циклов:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если [math]+D_ \lt D_>[/math] , то [math]
При этом вычисляются минимумы из двух чисел [math]min(+D_>, D_)[/math] и их значения становятся новыми значениями элементов смежной матрицы.
1.5 Схема реализации последовательного алгоритма
matrix - матрица смежности, numberOfVert - число вершин в графе
1.6 Последовательная сложность алгоритма
Время выполнения этой программы, очевидно, имеет порядок [math]O(n^3)[/math] , поскольку в ней практически нет ничего, кроме вложенных друг в друга трех циклов.
1.7 Информационный граф

На приведенном далее информационном графе нижний уровень параллелизма обозначен в горизонтальных плоскостях. Множество всех плоскостей представляет собой верхний уровень параллелизма (операции в каждой плоскости могут выполняться параллельно). Верхний уровень параллелизма заключается в параллельном подсчете дистанций для различных элементов матрицы смежности, и на рисунке отмечен разными плоскостями.
1.8 Ресурс параллелизма алгоритма
Первый подход. В распоряжении имеется такое количество процессоров, что можно отдать каждому ровно по одному элементу [math]D_[/math] , чтобы он считал для этого элемента минимум.
Второй подход. В распоряжении ограниченное количество процессов. В этом случае грамотным решением будет отдать каждому процессору(или процессу) по одной строке матрицы смежности. Пусть каждый процесс посчитает минимумы в своей строке матрицы и отдаст результаты корневому процессу, это прилично ускорит работу алгоритма.
Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы [math]D[/math] . Всего в подзадачах [math][/math] таких элементов, число итераций алгоритма равно [math]n[/math] , таким образом, показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид ( [math]p[/math] – число процессоров): [math][/math] , [math][/math] .
1.10 Свойства алгоритма
Алгоритм может распознавать наличие отрицательных циклов: такой цикл существует, если один из диагональных элементов матрицы расстояний становится меньше нуля.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
Возможность обрабатывать фрагменты независимо означает хорошую масштабируемость алгоритма. Сдерживающие факторы:
1)Пропускная способность памяти при чтении данных графа.
2)Соперничество потоков при выполнении атомарных операций с памятью.
3)Синхронизация после каждого подшага алгоритма.
Алгоритм Флойда-Уоршелла обладает большим потенциалом масштабируемости, так как вычисление кратчайших путей можно распределить между независимыми процессами вплоть до вычисления каждым отдельным процессом одного элемента матрицы смежности.
2.4.2 Масштабируемость реализации алгоритма
Проведём исследование масштабируемости параллельной реализации алгоритма. Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова. Сильная масштабируемость показывает, как меняется время решения задачи с увеличением количества процессоров (или вычислительных узлов) при неизменном общем объёме задачи.
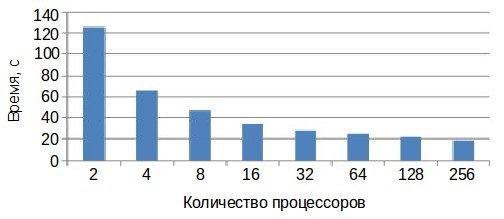
Сравнение времени параллельной работы алгоритма Флойда-Уоршелла в зависимости от количества процессоров.
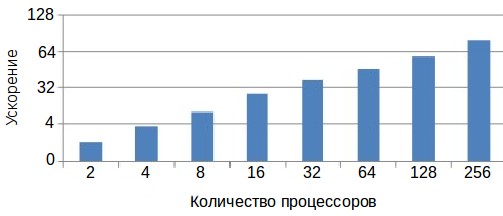
Как видно из представленных графиков параллельный алгоритм сильно масштабируем.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- C++: Boost Graph Library (функция floyd_warshall_shortest ).
- Python: NetworkX (функция floyd_warshall ).
- Java: JGraphT (класс FloydWarshallShortestPaths ).
3 Литература
- ↑ Roy, Bernard. “Transitivité Et Connexité.” Comptes Rendus De l'Académie Des Sciences 249 (1959): 216–218.
- ↑ Warshall, Stephen. “A Theorem on Boolean Matrices.” Journal of the ACM 9, no. 1 (January 1, 1962): 11–12. doi:10.1145/321105.321107.
- ↑ Floyd, Robert W. “Algorithm 97: Shortest Path.” Communications of the ACM 5, no. 6 (June 1, 1962): 345. doi:10.1145/367766.368168.
Навигация
Персональные инструменты
Пространства имён
Варианты
Просмотры
Поиск
Навигация
Хранилище файлов
Инструменты
На других языках
Алгоритм Флойда (алгоритм Флойда–Уоршелла) — алгоритм нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл. Алгоритм работает за [math] \Theta(n^3) [/math] времени и использует [math] \Theta(n^2) [/math] памяти. Разработан в 1962 году.
Содержание

Дан взвешенный ориентированный граф [math] G(V, E) [/math] , в котором вершины пронумерованы от [math]1[/math] до [math]n[/math] .
[math]\omega_ = \begin \textuv ,& \text uv \in E \\ +\infty ,& \text uv \notin E \end[/math]
Требуется найти матрицу кратчайших расстояний [math] d [/math] , в которой элемент [math] d_ [/math] либо равен длине кратчайшего пути из [math] i [/math] в [math] j [/math] , либо равен [math] +\infty [/math] , если вершина [math] j [/math] не достижима из [math] i [/math] .
Обозначим длину кратчайшего пути между вершинами [math] u [/math] и [math] v [/math] , содержащего, помимо [math]u[/math] и [math]v[/math] , только вершины из множества [math] \ < 1 .. i \>[/math] как [math]d_^[/math] , [math]d_^ = \omega_[/math] .
На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер — [math] i [/math] ) и для всех пар вершин [math]u[/math] и [math]v[/math] вычислять [math] d_^ = \min(d_^, d_^ + d_^) [/math] . То есть, если кратчайший путь из [math]u[/math] в [math]v[/math] , содержащий только вершины из множества [math] \ < 1 .. i \>[/math] , проходит через вершину [math]i[/math] , то кратчайшим путем из [math] u [/math] в [math] v [/math] является кратчайший путь из [math] u [/math] в [math] i [/math] , объединенный с кратчайшим путем из [math] i [/math] в [math] v [/math] . В противном случае, когда этот путь не содержит вершины [math] i [/math] , кратчайший путь из [math]u[/math] в [math]v[/math] , содержащий только вершины из множества [math] \ < 1 .. i \>[/math] является кратчайшим путем из [math]u[/math] в [math]v[/math] , содержащим только вершины из множества [math] \ < 1 .. i-1 \>[/math] .
В итоге получаем, что матрица [math] d^ [/math] и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества [math] \ < 1..n \>[/math] , что есть попросту все вершины графа. Такая реализация работает за [math] \Theta(n^3) [/math] времени и использует [math] \Theta(n^3) [/math] памяти.
Утверждается, что можно избавиться от одной размерности в массиве [math] d [/math] , т.е. использовать двумерный массив [math]d_[/math] . В процессе работы алгоритма поддерживается инвариант [math]\rho(u, v) \leqslant d_ \leqslant d_^[/math] , а, поскольку, после выполнения работы алгоритма [math] \rho(u, v) = d_^ [/math] , то тогда будет выполняться и [math] \rho(u, v) = d_ [/math] .
В течение работы алгоритма Флойда выполняются неравенства: [math]\rho(u, v) \leqslant d_
После инициализации все неравенства, очевидно, выполняются. Далее, массив [math] d [/math] может измениться только в строчке 5.
Докажем второе неравенство индукцией по итерациям алгоритма.
Пусть также [math]d'_[/math] — значение [math]d_[/math] сразу после [math]i - 1[/math] итерации.
Покажем, что [math] d_ \leqslant d_^ [/math] , зная, что [math] d'_ \leqslant d_^ <(i - 1)>[/math] .
Рассмотрим два случая:
- Значение [math] d_^ [/math] стало меньше, чем [math] d_^ <(i - 1)>[/math] . Тогда [math] d_^ = d_^ + d_^ \geqslant [/math] (выполняется на шаге [math] i - 1 [/math] , по индукционному предположению) [math] \geqslant d'_ + d'_ \ge[/math] (в силу выполнения 7-ой строчки алгоритма на [math]i[/math] -ой итерации и невозрастания элементов массива [math] d [/math] ) [math]\geqslant d_[/math] .
- В ином случае всё очевидно: [math] d_^ = d_^ <(i - 1)>\geqslant d'_ \geqslant d_ [/math] , и неравенство тривиально.
Докажем первое неравенство от противного.
Пусть неравенство было нарушено, рассмотрим момент, когда оно было нарушено впервые. Пусть это была [math]i[/math] -ая итерация и в этот момент изменилось значение [math]d_[/math] и выполнилось [math]\rho(u,v) \gt d_[/math] . Так как [math]d_[/math] изменилось, то [math]d_ = d_ + d_ \ge[/math] (так как ранее [math]\forall u, v \in V: \rho(u,v) \leqslant d_[/math] ) [math]\geqslant \rho(u, i) + \rho(i, v) \ge[/math] (по неравенству треугольника) [math]\geqslant \rho(u, v)[/math] .
Данная реализация работает за время [math] \Theta(n^3) [/math] , но требует уже [math] \Theta(n^2) [/math] памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении [math] \Theta [/math] весьма мала.
| [math]i = 0[/math] | [math]i = 1[/math] | [math]i = 2[/math] | [math]i = 3 [/math] | [math]i = 4[/math] |
| [math]\begin \times & 1 & 6 & \infty \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end[/math] | [math]\begin \times & 1 & 6 & \infty \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end[/math] | [math]\begin \times & 1 & \bf & \bf \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end[/math] | [math]\begin \times & 1 & 5 & 2 \\ \infty & \times & 4 & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end[/math] | [math]\begin \times & 1 & \bf & 2 \\ \infty & \times & \bf & 1 \\ \infty & \infty & \times & \infty \\ \infty & \infty & 1 & \times \\ \end[/math] |
Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив [math]next[/math] , в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из [math]u[/math] в [math]v[/math] по кратчайшему пути.
При наличии цикла отрицательного веса в матрице [math] D [/math] появятся отрицательные числа на главной диагонали.
Из доказательства следует, что для поиска цикла отрицательного веса необходимо, после завершения работы алгоритма, найти вершину [math] i [/math] , для которой [math] d[i][i] \lt 0 [/math] , и вывести кратчайший путь между парой вершин [math] (i, i) [/math] . При этом стоит учитывать, что при наличии отрицательного цикла расстояния могут уменьшаться экспоненциально. Для предотвращения переполнения все вычисления стоит ограничивать снизу величиной [math]-\infty[/math] , либо проверять наличие отрицательных чисел на главной диагонали во время подсчета.
Сформулируем нашу задачу в терминах графов: рассмотрим граф [math]G=(V,\; E),\; |V| = n[/math] , соответствующий отношению [math]R[/math] . Тогда необходимо найти все пары вершин [math](x, y) [/math] , соединенных некоторым путем. Иными словами, требуется построить новое отношение [math]T[/math] , которое будет состоять из всех пар [math](x, y) [/math] таких, что найдется последовательность [math]x = x_0, x_1, \dots, x_k = y [/math] , где [math] (x_, x_i) \in R, i = 1, 2, \dots, k [/math] .
Изначально матрица [math]W[/math] заполняется соответственно отношению [math]R[/math] , то есть [math]W[i][j] = [(i, j) \in R] [/math] . Затем внешним циклом перебираются все элементы [math]k[/math] множества [math]X[/math] и для каждого из них, если он может использоваться, как промежуточный для соединения двух элементов [math]i[/math] и [math]j[/math] , отношение [math]T[/math] расширяется добавлением в него пары [math](i, j)[/math] .
Назовем промежуточной вершину некоторого пути $p = \left \langle v_0, v_1, \dots, v_k \right \rangle$, принадлежащую множеству вершин этого пути и отличающуюся от начальной и конечной вершин, то есть принадлежащую $\left \ < v_1, v_2, \dots, v_\right \>$. Рассмотрим произвольную пару вершин $i, j \in V$ и все пути между ними, промежуточные вершины которых принадлежат множеству вершин с номерами $\left \< 1, 2, \dots, k \right \>$. Пусть $p$ — некоторый из этих путей. Докажем по индукции (по числу промежуточных вершин в пути), что после $i$-ой итерации внешнего цикла будет верно утверждение — если в построенном графе между выбранной парой вершин есть путь, содержащий в качестве промежуточных только вершины из множества вершин с номерами $\left \ < v_1, v_2, \dots, v_\right \>$, то между ними будет ребро.
- База индукции. Если у нас нет промежуточных вершин, что соответствует начальной матрице смежности, то утверждение выполнено: либо есть ребро (путь не содержит промежуточных вершин), либо его нет.
- Индуктивный переход. Пусть предположение выполнено для $i = k - 1$. Докажем, что оно верно и для $i = k$ Рассмотрим случаи (далее под вершиной будем понимать ее номер для простоты изложения):
- $k$ не является промежуточной вершиной пути $p$. Тогда все его промежуточные пути принадлежат множеству вершин с номерами $\left \ < 1, 2, \dots, k-1 \right \>\subset \left \< 1, 2, \dots, k \right \>$, то есть существует путь с промежуточными вершинами в исходном множестве. Это значит $W[i][j]$ будет истиной. В противном случае $W[i][j]$ будет ложью и на k-ом шаге ею и останется.
- $k$ является промежуточной вершиной предполагаемого пути $p$. Тогда этот путь можно разбить на два пути: $i \xrightarrow k \xrightarrow j$. Пусть как $p_1$, так и $p_2$ существуют. Тогда они содержат в качестве промежуточных вершины из множества $\left \ < 1, 2, \dots, k-1 \right \>\subset \left \< 1, 2, \dots, k \right \>$ (так как вершина $k$ — либо конечная, либо начальная, то она не может быть в множестве по нашему определению). Тогда $W[i][k]$ и $W[k][j]$ истинны и по индуктивному предположению посчитаны верно. Тогда и $W[i][j]$ тоже истина. Пусть какого-то пути не существует. Тогда пути $p$ тоже не может существовать, так как добраться, например, от вершины $i$ до $k$ по вершинам из множества $\left \< 1, 2, \dots, k \right \>$ невозможно по индуктивному предположению. Тогда вся конъюнкция будет ложной, то есть такого пути нет, откуда $W[i][j]$ после итерации будет ложью.
Таким образом, после завершения внешнего цикла у нас будет $W[i][j] = true$, если между этими вершинами есть путь, содержащий в качестве промежуточных вершин из множества всех остальных вершин графа, что и есть транзитивное замыкание.
Строки матрицы [math]W[/math] можно хранить с помощью массива битовых масок длиной [math]k[/math] . Тогда последний цикл будет выполняться в [math]k[/math] раз быстрее и сложность алгоритма снижается до [math]O\Big(\dfrac\Big)[/math] .
Пример реализации оптимизации с помощью битмасок:В данной реализации длина битовой маски [math]k[/math] равна [math]32[/math] битам. Последний цикл делает в [math]32[/math] раза меньше операций — сложность алгоритма [math]O\Big(\dfrac\Big)[/math] .
Рассматриваемый алгоритм иногда называют алгоритмом Флойда -Уоршелла. Алгоритм Флойда -Уоршелла является алгоритмом на графах, который разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом. Он служит для нахождения кратчайших путей между всеми парами вершин графа .
Метод Флойда непосредственно основывается на том факте, что в графе с положительными весами ребер всякий неэлементарный (содержащий более 1 ребра ) кратчайший путь состоит из других кратчайших путей .
Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя вершинами графа .
В алгоритме Флойда используется матрица A размером nxn , в которой вычисляются длины кратчайших путей . Элемент A[i,j] равен расстоянию от вершины i к вершине j , которое имеет конечное значение , если существует ребро (i,j) , и равен бесконечности в противном случае.
Алгоритм Флойда
Основная идея алгоритма. Пусть есть три вершины i, j, k и заданы расстояния между ними. Если выполняется неравенство A[i,k]+A[k,j], то целесообразно заменить путь i->j путем i->k->j . Такая замена выполняется систематически в процессе выполнения данного алгоритма.
Шаг 0. Определяем начальную матрицу расстояния A0 и матрицу последовательности вершин S0 . Каждый диагональный элемент обеих матриц равен 0, таким образом, показывая, что эти элементы в вычислениях не участвуют. Полагаем k = 1 .
![]()
Основной шаг k . Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения замены описанной выше, ко всем элементам A[i,j] матрицы Ak-1 . Если выполняется неравенство , тогда выполняем следующие действия:
- создаем матрицу Ak путем замены в матрице Ak-1 элемента A[i,j] на сумму A[i,k]+A[k,j] ;
- создаем матрицу Sk путем замены в матрице Sk-1 элемента S[i,j] на k . Полагаем k = k + 1 и повторяем шаг k .
Таким образом, алгоритм Флойда делает n итераций, после i -й итерации матрица А будет содержать длины кратчайших путей между любыми двумя парами вершин при условии, что эти пути проходят через вершины от первой до i -й. На каждой итерации перебираются все пары вершин и путь между ними сокращается при помощи i -й вершины ( рис. 45.2).
Заметим, что если граф неориентированный, то все матрицы, получаемые в результате преобразований симметричны и, следовательно, достаточно вычислять только элементы, расположенные выше главной диагонали.
Если граф представлен матрицей смежности , то время выполнения этого алгоритма имеет порядок O(n 3 ) , поскольку в нем присутствуют вложенные друг в друга три цикла .
Переборные алгоритмы
Переборные алгоритмы по сути своей являются алгоритмами поиска, как правило, поиска оптимального решения. При этом решение конструируется постепенно. В этом случае обычно говорят о переборе вершин дерева вариантов. Вершинами такого графа будут промежуточные или конечные варианты, а ребра будут указывать пути конструирования вариантов.
Рассмотрим переборные алгоритмы, основанные на методах поиска в графе, на примере задачи нахождения кратчайшего пути в лабиринте.
Постановка задачи.
![A[i,j]=\infty]()
Лабиринт, состоящий из проходимых и непроходимых клеток, задан матрицей A размером mxn . Элемент матрицы A[i,j]=0 , если клетка (i,j) проходима. В противном случае .
Требуется найти длину кратчайшего пути из клетки (1, 1) в клетку (m, n) .
Фактически дана матрица смежности (только в ней нули заменены бесконечностями, а единицы – нулями). Лабиринт представляет собой граф .
Вершинами дерева вариантов в данной задаче являются пути, начинающиеся в клетке (1, 1) . Ребра – показывают ход конструирования этих путей и соединяют два пути длины k и k+1 , где второй путь получается из первого добавлением к пути еще одного хода.
Перебор с возвратом
Данный метод основан на методе поиска в глубину . Перебор с возвратом считают методом проб и ошибок ("попробуем сходить в эту сторону: не получится – вернемся и попробуем в другую"). Так как перебор вариантов осуществляется методом поиска в глубину , то целесообразно во время работы алгоритма хранить текущий путь в дереве. Этот путь представляет собой стек Way.
Также необходим массив Dist , размерность которого соответствует количеству вершин графа , хранящий для каждой вершины расстояние от нее до исходной вершины.
Пусть текущей является некоторая клетка (в начале работы алгоритма – клетка (1, 1) ). Если для текущей клетки есть клетка-сосед Neighbor , отсутствующая в Way , в которую на этом пути еще не ходили, то добавляем Neighbor в Way и текущей клетке присваиваем Neighbor , иначе извлечь из Way .
Приведенное выше описание дает четко понять, почему этот метод называется перебором с возвратом. Возврату здесь соответствует операция "извлечь из Way ", которая уменьшает длину Way на 1.
Перебор заканчивается, когда Way пуст и делается попытка возврата назад. В этой ситуации возвращаться уже некуда ( рис. 45.3).
Way является текущим путем, но в процессе работы необходимо хранить и оптимальный путь OptimalWay .
Усовершенствование алгоритма можно произвести следующим образом: не позволять, чтобы длина Way была больше или равна длине OptimalWay . В этом случае, если и будет найден какой-то вариант, он заведомо не будет оптимальным. Такое усовершенствование в общем случае означает, что как только текущий путь станет заведомо неоптимальным, надо вернуться назад. Данное улучшение алгоритма позволяет во многих случаях сильно сократить перебор.
Наиболее часто используемое название, метод получил в честь двух американских исследователей Роберта Флойда и Стивена Уоршелла, одновременно открывших его в 1962 году. Реже встречаются другие варианты наименований: алгоритм Рой – Уоршелла или алгоритм Рой – Флойда. Рой – фамилия профессора, который разработал аналогичный алгоритм на 3 года раньше коллег (в 1959 г.), но это его открытие осталось безвестным.
Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.
Для реализации алгоритма Флойда – Уоршелла сформируем матрицу смежности D[][] графа G=(V, E), в котором каждая вершина пронумерована от 1 до |V|. Эта матрица имеет размер |V|´|V|, и каждому ее элементу D[i][j] присвоен вес ребра, идущего из вершины i в вершину j. По мере выполнения алгоритма, данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины i в вершину j (отказ от выделения специального массива для этой цели сохранит память и время).
Теперь, перед составлением основной части алгоритма, необходимо разобраться с содержанием матрицы кратчайших путей. Поскольку каждый ее элемент D[i][j] должен содержать наименьший из имеющихся маршрутов, то сразу можно сказать, что для единичной вершины он равен нулю, даже если она имеет петлю (отрицательные циклы не рассматриваются), следовательно, все элементы главной диагонали (D[i][i]) нужно обнулить.
А чтобы нулевые недиагональные элементы (матрица смежности могла иметь нули в тех местах, где нет непосредственного ребра между вершинами i и j) сменили по возможности свое значение, определим их равными бесконечности, которая в программе может являться, например, максимально возможной длинной пути в графе, либо просто – большим числом.
Ключевая часть алгоритма, состоя из трех циклов, выражения и условного оператора, записывается довольно компактно:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если D[i][k]+D[k][j]Алгоритм Флойда-Уоршелла — это метод нахождения самых коротких расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами, с использованием метода динамического программирования.
Введение
Использование алгоритма Флойда – Уоршелла позволяет определить самые короткие пути между любой парой вершин графа. Согласно условию задачи, имеем неориентированный или ориентированный взвешенный граф G, который имеет n вершин. Необходимо определить величину всех кратчайших путей d(i, j) между вершинами i и j, при условии отсутствия в графе циклов с отрицательными весами (в этом случае решения для некоторых пар вершин могут быть бесконечно малыми, то есть несуществующими). Данный алгоритм описали в своих работах независимо друг от друга и примерно в одно и тоже время Роберт Флойд и Стивен Уоршелл в 1962-м году. В их честь и назвали алгоритм, именуемый и сегодня алгоритмом Флойда – Уоршелла. Однако следует заметить, что ещё в 1959-ом году Бернардом Роем был разработан почти аналогичный алогитм, но он не был тогда никем замечен.
Алгоритм Флойда – Уоршелла
Главный идейный постулат алгоритма заключается в разделении процедуры нахождения самых коротких путей на отдельные фазы. В начале к-той фазы (где к = 1…n) предполагается, что есть матрица расстояний d [ ] , в которой хранятся величины самых коротких путей, содержащих как внутренние, только вершины из набора < 1, 2,…, k – 1>. Все вершины графа пронумерованы с цифры один. То есть, в начале к-той фазы значение d[i][j], равняется величине самого короткого пути между вершинами i и j, при условии, что этот путь содержит только вершины, имеющие номера меньше К (начальная и конечная точка маршрута при этом не учитываются). Достаточно просто проверить, что для выполнения этого условия в первой фазе, надо в матрицу дистанций d[ ] [ ] вписать матрицу смежности графа: d[i][j]=g[i][j] — цена ребра между вершинами i и j. В случае, если есть вершины, не соединённые рёбрами, то необходимо вписать бесконечное значение. Расстояние из вершины i в вершину i (то есть в саму себя) необходимо всегда принимать за нуль, это важно для работы алгоритма.
Готовые работы на аналогичную тему
Предположим, что алгоритм находится в к-той фазе, и необходимо сделать перерасчёт матрицы d[ ] [ ] для её соответствия условиям для к+1-ой фазы. Произведём фиксацию некоторых вершин i и j. Получается пара абсолютно различных вариантов:
- Самый короткий маршрут из вершины i к вершине j, который имеет разрешение добавочно пройти через вершины < 1,2,…,k>, совпал с самым коротким маршрутом, с разрешением прохождения через вершины набора < 1,2,…,k – 1>. Это означает, что значение d[i][j] останется прежним при смене фазы с к-той на к+1-ую фазу.
- Вновь созданный самый короткий маршрут становится лучше, чем прежний маршрут.
То есть выходит, что весь объём работ, подлежащих выполнению в К-той фазе, заключается в переборе всех пар вершин и пересчёте размеров самых коротких путей среди них. В итоге по завершению функционирования n-ой фазы, в матрице дистанций d[i][j] окажется размер самого короткого маршрута от i до j, или бесконечность, в случае отсутствия маршрута между вершинами. И напоследок надо отметить, что возможно и не формировать новую матрицу nеw_d[ ][ ] в качестве хранилища самых коротких маршрутов на к-той фазе. Всё можно менять и хранить сразу в матрице d[ ][ ]. Поскольку, в случае улучшения (уменьшения) какого-либо числа в матрице дистанций, не происходит ухудшения размера самого короткого маршрута для каких-либо иных пар вершин, которые обрабатывались позже. Чтобы вычислить асимптотику этого алгоритма, необходимо воспользоваться формулой: $O(n^3)$
Программное выполнение алгоритма
![Код. Автор24 — интернет-биржа студенческих работ]()
Рисунок 1. Код. Автор24 — интернет-биржа студенческих работ
![Код. Автор24 — интернет-биржа студенческих работ]()
Рисунок 2. Код. Автор24 — интернет-биржа студенческих работ
Восстановление маршрутов
Читайте также:



![A[i,j]=\infty](https://intuit.ru/sites/default/files/tex_cache/db2c035e62916aae55881f5dd7d3f700.jpg)

