Задачи на построение сечений параллелепипеда 10 класс конспект

Обновлено: 07.07.2024

Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.

Сечением поверхности геометрических тел называется – плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.

Основная литература:

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Учебник Геометрия 10-11 кл.– М.: Просвещение, 2014.

Дополнительная литература:

Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.

Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

В дельнейшем несколько уроков нашего курса будет посвящены многогранникам- поверхностям геометрических тел, составленным из многоугольников. Но до более подробного изучения многогранников мы познакомимся с двумя из них- тетраэдром и параллелепипедом. Нам данные тела дадут возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей.

Давайте вспомним, что мы понимали под многоугольником в планиметрии. Многоугольник мы рассматривали либо как замкнутую линию без самопересечений, либо как часть плоскости, ограниченную этой линией, включая ее саму.

Мы будем использовать второе толкование многоугольника при рассмотрении поверхностей и тел в пространстве. При таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность.

Давайте рассмотрим изображенную фигуру и ответим на несколько вопросов.

Итак, поверхность данной фигуры состоит из четырёх треугольников DАВ, DВС, DАС и АВС.

из вершин- их у него 4- А, B, C, D;
из ребер- их у него 6- AB, BC, AC, AD, BD, CD;
из граней- их у него 4- треугольники ∆АВС, ∆DАС, ∆DВС, ∆DАВ.

Мы с вами выяснили из элементов состоит наша фигура тетраэдр. Теперь сформулируем определение.

Определение. Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

Говорят, что рёбра АD и ВС, АВ и CD, и т.д.- противоположные.

Считается АВС - основание, остальные грани - боковые.

Изображается тетраэдр обычно так (рис. 1).

Рисунок 1 – изображение тетраэдра.

Математика, в частности геометрия, является мощнейшим инструментом в познании мира. Различные геометрические формы находят свое практическое приспособление в различных областях знания: архитектуре, скульптуре, живописи. И тетраэдр тому доказательство. Так же мы можем наблюдать тетраэдр в повседневной жизни (рис. 2).

Форма пакета молока

Рисунок 2 - тетраэдр в повседневной жизни

Параллелепипед.

Прежде чем начать изучать параллелепипед вспомним определение параллелограмма и его свойства.

Определение. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом (рис. 3).

Рисунок 3 – параллелограмм

1. Противоположные стороны параллелограмма равны:

2. Противоположные углы параллелограмма равны:

3. Диагонали параллелограмма точкой пересечения делятся пополам:

Диагональ делит параллелограмм на два равных треугольника:

треугольники ABC и CDA равны.

Сумма углов, прилежащих к одной стороне параллелограмма, равна 180⁰: ∟A+∟D=180°

6. Накрест лежащие углы при диагонали равны:

А теперь перейдем к параллелепипеду.

Рассмотрим два равных параллелограмма ABCD и A₁B₁C₁D₁, расположенных в параллельных плоскостях так, что отрезки AA_1, BB_1, CC₁ и DD₁ параллельны.

Давайте рассмотрим изображенную фигуру (рис. 4).

Рисунок 4 – параллелепипед и его диагонали

АВСDA₁B₁C₁D₁: поверхность, составленная из двух равных параллелограммов АВСD и A₁B₁C₁D₁, лежащих в параллельных плоскостях и четырёх параллелограммов.

Все параллелограммы - грани, их стороны - рёбра, их вершины - вершины параллелепипеда.

Считается: АВСD и A₁B₁C₁D₁ - основания, остальные грани - боковые.

Определение. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда:
A₁C, D₁B, AC₁, DB₁.

Параллелепипед – слово греческого происхождения, параллел – идущий рядом, епипед – плоскость.

Определение.Параллелепипед- этошестигранник с параллельными и равными противоположными гранями.

Следует отметить, что многоугольник в пространстве представляет собой плоскую поверхность, а тетраэдр и параллелепипед – поверхности, составленные из плоских поверхностей (соответственно треугольников и параллелограммов).

Способы изображения параллелепипеда

Параллелепипед, в основании которого лежит ромб

Параллелепипед, в основании которого лежит квадрат

Параллелепипед,в основании которого лежит прямоугольник или параллелограмм

Параллелепипед, у которого все грани — равные квадраты

Можно сделать вывод, что параллелепипеды делятся на (рис. 5)

Рисунок 5 – виды параллелепипедов

Свойства параллелепипеда

Противоположные грани параллелепипеда параллельны и равны.
Все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

Доказательство 1

В параллелепипеде ABCDA₁B₁C₁D₁грани ВВ₁С₁С и AA₁D₁D параллельны (рис. 6), потому что две пересекающиеся прямые ВВ₁ и В₁С₁ одной грани параллельны двум пересекающимся прямым АА₁ и A₁D₁ другой; эти грани и равны, так как В₁С₁ = A₁D₁, В₁В= А₁А (как противоположные стороны параллелограммов) и ∟ ВВ₁С₁= ∟АA₁D₁.

Рисунок 6 – чертеж к доказательству свойства 1

Доказательство 2

Возьмём какие-нибудь две диагонали, например АС₁ и ВD₁, и проведём вспомогательные прямые АD₁ и ВС₁ (рис. 7).

Так как рёбра АВ и D₁С₁ соответственно равны и параллельны ребру DС, то они равны и параллельны между собой; вследствие этого фигура АD₁С₁В есть параллелограмм, в котором прямые С₁А и ВD₁ —диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам.

Возьмём теперь одну из этих диагоналей, например АС₁, с третьей диагональю, положим, с В₁D. Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B₁D и АС₁ и диагонали АС₁ и BD₁(которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали
АС₁. Наконец, взяв эту же диагональ АС₁ с четвёртой диагональю А₁С, мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали АС₁. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.

Рисунок 7 – чертеж к доказательству свойства 2

Задачи на построение сечений.

Определение. Сечением поверхности геометрических тел называется - плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.

Взаимное расположение многогранника и секущей плоскости:

Многогранник и плоскость не имеют общих точек.
Многогранник и плоскость имеют одну общую точку-вершину многогранника.
Многогранник и плоскость имеют общую грань.
Многогранник и плоскость имеют общий отрезок-ребро многогранника.

Виды сечений:

сечение параллельное плоскости основания,
диагональное сечение,
сечение, параллельное плоскости грани,
произвольное сечение.

Фигуры, которые получаются в результате сечения:

1. треугольник;
2. четырехугольник;
3. пятиугольник;
4. шестиугольник.

Один из методов построения сечений, который мы рассмотрим- метод следа.

Рассмотрим метод следов, применяемый при построении сечений многогранников, а именно при построении сечения куба плоскостью.

Что такое метод следов? При построении сечений многогранников в качестве вспомогательной прямой часто используется след секущей плоскости (в плоскости грани, удобной для рассмотрения). Такой метод построения сечений называется методом следа.

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R (рис. 8).

Рисунок 8 –чертеж к задаче №1

Построим след секущей плоскости на плоскость нижнего основания параллелепипеда. Рассмотрим грань АА₁В₁В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S₁, принадлежащую следу.
Аналогично получаем точку S₂ пересечением прямых QR и BC.
Прямая S₁S₂ - след секущей плоскости на плоскость нижнего основания параллелепипеда.
Прямая S₁S₂ пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА₁D₁D. Аналогично получаем TU и RT.
PQRTU – искомое сечение.

Основные правила построения сечений методом следа:

Если даны (или уже построены) две точки плоскости сечения на одной грани многогранника, то след сечения этой плоскости – прямая, проходящая через эти три точки.
Если дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определенной боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью ( точка пересечения данного следа с общей прямой основания и данной боковой грани)
Точку пересечения плоскости сечения с основанием можно определить как точку пересечения какой-либо прямой в плоскости сечения с ее проекцией на плоскость основания.

То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.

Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС.

Рисунок 9 – чертеж к задаче №2

Решение:
Для решения построим вспомогательную плоскость DМN (рис. 10). Пусть прямая DМ пересекает прямую АВ в точке К. Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.

Примеры и разбор решения заданий тренировочного модуля

Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.

Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС (рис. 11). В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.

Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р₁ и Р₂. Соединяем Р₁ и М и на продолжении получаем точку М₁. Соединяем точку Р₂ и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.

Рисунок 10 – чертеж к примеру 1 (первый случай)

Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС (рис. 12). Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р₁Р₂, тогда прямая Р₁Р₂ параллельна данной прямой MN.

Рисунок 11 – чертеж к примеру 1 (второй случай)

Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите, что эта плоскость пересекает грани SAB и SBC по параллельным прямым.

Доказательство

Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N (рис. 13).
По теореме (о параллельных прямых) линия пересечения параллельна SB.
В плоскость SBC через т. N проходит NQ||SB.
Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. M (прямая MP). По теореме (о параллельных прямых) линия пересечения параллельна SB.

следовательно, PM||NQ.Утверждение доказано.

Двое учащихся у доски выполняют задание, подобное домашней работе.

Задание 1.

Рисунок 1

Дано: А a ; М a ; Р a ; С a ; В a .

Построить точку пересечения прямой МР с плоскостью (АВС).

Задание 2.

Рисунок 2

Дано: Е b ; F b ; М a .

Построить линии пересечения плоскости (EFM) с плоскостями a и b .

а) плоскости (АВС) и (А' В' С') параллельны;
б) прямые А'В' и СD параллельны;
в) прямые А'' В''и D'С'параллельны;
г) точка В' принадлежит плоскости А'СD;
д) плоскости (А''В''С'), (А'В'С') и (АВС) пересекаются по одной прямой ;
е) плоскости (А''В''С'') и (DСА') пересекаются по прямой, параллельной прямой CD.

а) прямую пересечения плоскостей (А'В'С') и (СDD');
б) прямую пересечения плоскостей (D'OD) и (АВС);
в) точку пересечения плоскости АDС и прямой В'В;
г) точку пересечения плоскости (ВВ'D') и прямой СD.

II. Изучение нового материала.

1. Введение понятия секущей плоскости и сечения ( слайд 2 ).

2. Работа по рисункам (рисунок 3 нарисован заранее с обратной стороны доски) и модели куба.

Учитель. Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе?

Первые три рисунка учитель показывает на доске, последние два ученики выполняют в тетрадях самостоятельно.

Для построения сечения достаточно построить точки пересечения секущей плоскости с рёбрами куба (тетраэдра, параллелепипеда).
Через полученные точки, лежащие в одной грани, провести отрезки.
Многоугольник, ограниченный данными отрезками, и есть построенное сечение.
Если секущая плоскость пересекает противоположные грани куба (параллелепипеда) по каким-либо отрезкам, то эти отрезки параллельны.

3. Применяя полученные выводы, построить сечение параллелепипеда плоскостью, проходящей через указанные точки (рисунок 4).

Учитель выполняет построение на доске, учащиеся в своих тетрадях. Можно вызвать к доске одного из учеников.

4. Решение задачи №79 (а). Один ученик выполняет чертёж на доске.

Учитель. Изобразите параллелепипед ABCDA' B'C'D' и постройте его сечение плоскостью АВС'. Докажите, что полученное сечение является параллелограммом.

При объяснении построения и при доказательстве учащиеся должны учитывать свойство граней параллелепипеда и правила для построения сечений.

Построение сечений в тетраэдре по чертежам, заранее начерченных на доске (желательно с обратной стороны).

Ученики выполняют построения в тетрадях, учитель проверяет, при необходимости исправляет, помогает при затруднениях, оценивает учеников, выполнивших два или три задания.

При выполнении задания большинством учеников, чертежи выполняются и на доске одним из учеников.

5. Объяснение наиболее сложной задачи на построение сечения параллелепипеда плоскостью, проходящей через три данные точки. ( слайд 3 ).

Как построить прямую, по которой секущая плоскость пересекает плоскость нижнего основания?
По каким прямым секущая плоскость пересекает верхнее и нижнее основания параллелепипеда?
Через какую точку проходит прямая, параллельная прямой АЕ?

6. После показа построения ученики выполняют построение в тетрадях. (При необходимости слайд можно показать повторно).

7. Итог урока.

Давайте вспомним этапы построения сечений тетраэдра (параллелепипеда, куба). Какие многоугольники могут при этом получиться?

8. Задание на дом: § 4, п.14, решить задачи №79(б), 82, для более сильных учеников №114.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

ПЛАН-КОСПЕКТ УРОКА

ФИО (полностью) Пластун Сергей Владимирович

Предмет геометрия

Класс 10

Дата 21.11.17

Источники

Авторлары: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.

Авторы: Абылкасымова А.Е., Корчевский В.Е., Жумагулова З.А.

Авторлары: Шыныбеков А.Н.

Авторы: Шыныбеков А.Н.

Рассмотреть различные виды сечений параллелепипеда

Развивать умение сравнивать, анализировать, делать выводы.

Воспитывать уважительное отношение учащихся друг к другу в процессе коллективной деятельности.

воспитательная: нравственное воспитание учащихся, развитие коммуникативных умений, рефлексии, внимания, культуры и дисциплины умственного труда.

Форма: частично- поисковый

Оборудование: дидактические материалы

- Тип урока: изучение новой темы

Метод: частично поисковый

Оборудование: модели куба и прямоугольного параллелепипеда, мультимедийный проектор

СТРУКТУРА И ХОД УРОКА

иллюстрация, демонстрация и т. д.)

Мотивационное начало урока.

Вводная беседа с использованием презентации

Проверка домашнего задания

Повторение пройденного материала

Индивидуальная работа по карточкам

Подведение итогов, постановка домашнего задания

Организационный момент . Взаимное приветствие учителя и учащихся. Определение отсутствующих, проверка подготовленности учащихся к уроку, организация внимания учащихся

Проверка домашнего задания : Выявления уровня знаний учащимися заданного на дом материала; определение типичных недостатков в знаниях и причин их появления; ликвидация обнаруженных недочетов.

Всесторонняя проверка знаний : Стимулировать опрашиваемых и весь класс к овладения рациональными приемами умения и самообразования

Изучение новой темы

2.Вступительное слово учителя

На предыдущих уроках мы строили сечение тетраэдра плоскостью.

3. Повторение изученного материала.

Давайте повторим некоторые вопросы теории.

Что такое секущая плоскость? (Секущей плоскостью тетраэдра(параллелепипеда) называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра(параллелепипеда))

Как можно задать секущую плоскость(3 точками, прямой и не лежащей на ней точкой, 2 параллельными прямыми, 2 пересекающимися прямыми)

Что такое сечение тетраэдра (параллелепипеда)? ( Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра (параллелепипеда))

Какие многоугольники мы получали при построении сечений тетраэдра?

( треугольники и четырехугольники).

Проверить выполнение домашнего задания (устно) №106.

4. Изучение нового материала. Вовлечение учащихся в поисковую деятельность.

А какие многоугольники мы можем получить при построении сечений параллелепипеда? ( треугольники и четырех-, 5 -и 6-угольники )

Можем ли получить 7-угольное сечение? Почему?( ответы учащихся)

Мы предположили, что получатся треугольники и четырех, 5 и 6-угольники, нам это предположение нужно проверить, поэтому цели нашего урока (слайд 2)

Определить виды сечений параллелепипеда

Установить взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда

Научиться строить сечения

Начнем с треугольного сечения, как нужно расположить 3 точки, чтобы получить треугольное сечение? ( заслушать ответы учащихся)

(на ребрах исходящих из одной вершины или расположенных в 3 вершинах).

Давайте посмотрим как могут выглядеть такие сечения (слайд 3)

Как нужно расположить 3 точки, чтобы получить 4-угольное сечение ( на параллельных ребрах). Рассмотреть варианты учащихся.

При построении сечений параллелепипеда важно помнить следующее условие (слайд 4)

Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны.(Запишем это утверждение)

С учетом этого условия построим сечение, проходящее через точки М, N , K (слайд 5). Построение сечения происходит с комментированием учащихся.

5.Работа в парах. Поисковая деятельность.

Переходим к следующим двум сечениям: 5 и 6 –угольным.

Постройте в тетрадях параллелепипеды и попробуйте расположить точки так, что бы получить 5- или 6- угольные сечения, можно работать сообща.

(На выполнение этого задания отводится 5-7 минут. Учитель контролирует выполнение этого задания в каждой паре или привлекает к этому консультантов – помощников. Учащиеся в каждой паре должны представить варианты различных 5- и 6- угольных сечении. )

6. Защита проектов

Два ученика выполняют построение 5 и 6-угольные сечения на доске. Давайте рассмотрим другие варианты построения таких сечений.

(слайд 6 и 7, учитель объясняет ход построения).

7. Закрепление изученного материала.

Мы рассмотрели все виды сечений, переходим к более сложной задаче (чертеж на экране)

слайд 8 (построение записывает учитель, дети проговаривают построение вслух)

8. Самостоятельная работа(2 варианта)

слайд 9. Учащиеся выполняют работу в тетрадях, затем по готовым чертежам выполняют оценку работ.

10. Итог урока

11.Рефлексия

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 24 человека из 17 регионов

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 611 535 материалов в базе

Материал подходит для УМК

4.3. Задачи на построение сечений

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

08.12.2018 666
DOCX 56.5 кбайт
23 скачивания
Оцените материал:

Настоящий материал опубликован пользователем Пластун Сергей Владимирович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы

Время чтения: 0 минут

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Время чтения: 1 минута

Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ

Время чтения: 1 минута

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Время чтения: 1 минута

В Госдуме предложили ввести сертификаты на отдых детей от 8 до 17 лет

Время чтения: 1 минута

Россияне ценят в учителях образованность, любовь и доброжелательность к детям

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Задание 1. Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью BKL, где K – середина ребра AA 1 , а L – середина ребра СС 1 . Доказать, что построенное сечение – параллелограмм.

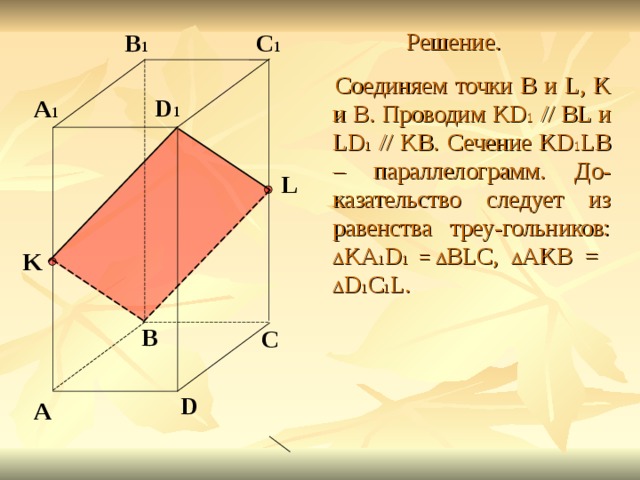
Соединяем точки B и L, K и B. Проводим KD 1 // BL и LD 1 // KB. Сечение KD 1 LB – параллелограмм. До-казательство следует из равенства треу-гольников:  KA 1 D 1 =   BLC,  AKB =  D 1 C 1 L.

Задание 2. Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через диагональ АС основания параллельно диагонали BD 1 . Доказать, что построенное сечение – равнобедренный треугольник, если основание параллелепипеда – ромб и углы ABB 1 и CBB 1 прямые.

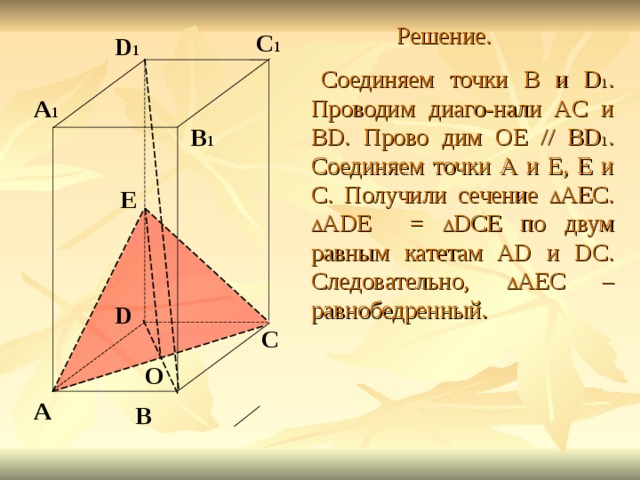
Соединяем точки B и D 1 . Проводим диаго-нали AC и BD. Прово дим OE // BD 1 . Соединяем точки А и Е, Е и С. Получили сечение  АЕС.  ADE =  DCE по двум равным катетам AD и DC. Следовательно,  АЕС – равнобедренный.

Задание 3. Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки В 1 и D 1 и середину ребра CD. Доказать, что построенное сечение – трапеция.

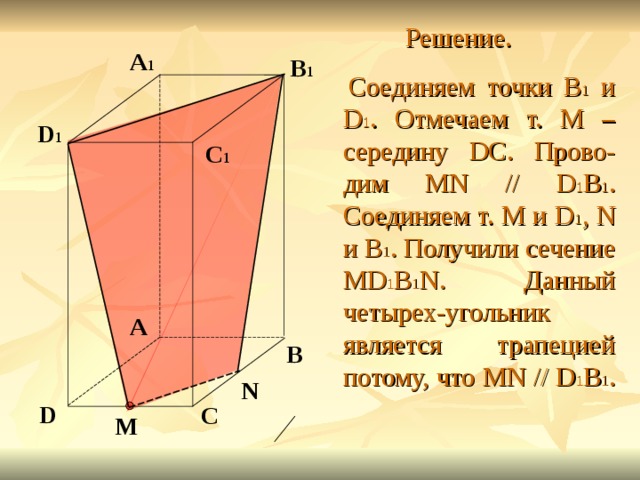
Соединяем точки B 1 и D 1 . Отмечаем т. М – середину DC. Прово-дим MN // D 1 B 1 . Соединяем т. M и D 1 , N и B 1 . Получили сечение MD 1 B 1 N. Данный четырех-угольник является трапецией потому, что MN // D 1 B 1 .

Читайте также: