Углы с сонаправленными сторонами угол между прямыми 10 класс конспект урока и презентация

Обновлено: 07.07.2024

Любая прямая a , лежащая в плоскости, разделяет плоскость на две части, называемые полуплоскостями. Прямая a называется границей каждой из этих полуплоскостей.

Это одна из аксиом планиметрии.

Два луча OA и O ₁ A ₁ в пространстве называются одинаково направленными (сонаправленными), если один из их содержит другой или они параллельны и лежат в одной полуплоскости с границей OO ₁ .

Теорема. Если стороны двух углов соответственно сонаправлены, то такие углы равны.

По условию теоремы нам даны углы АОВ и А₁О₁В₁ и известно что их стороны соответственно сонаправлены т.е. ОА и О₁А₁, ОВ и О₁В₁ – сонаправленные лучи

Доказать что данные углы равны

При доказательстве ограничимся случая, когда углы лежат в разных плоскостях.

1.Стороны углов сонаправлены, а значит параллельны. Проведем через них плоскости и как показано на чертеже.

Отметим на сторонах угла O произвольные точки A и B .

На соответствующих сторонах угла O ₁ отложим отрезки O ₁ A ₁ и O ₁ B ₁ равные соответственно О A и OB .

2. В плоскости a рассмотрим четырехугольник OAA ₁ O _1.

Так как противолежащие стороны OA и O ₁ A ₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник – параллелограмм и, следовательно, равны и параллельны стороны AA ₁ и OO ₁

3. В плоскости b , аналогично можно доказать, что OBB ₁ O ₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO ₁

4. Если две отрезка AA ₁ и BB ₁ равны параллельны третьему отрезку OO ₁ , значит они равны и параллельны, т. е. АА₁|| BB ₁ и AA ₁ = BB ₁ .

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁

5. из выше построенного и доказанного АВ=А₁В₁, О A = O ₁ A ₁ и OB = O ₁ B ₁ следуем что треугольники AOB и A ₁ O ₁ B ₁ . равны по трем сторонам, и поэтому О=О₁

Теорема. Если стороны двух углов соответственно сонаправлены, то такие углы равны.

1.Стороны углов сонаправлены, а значит параллельны, через них можно провести плоскости и .

Отметим на сторонах O точки A и B .

На соответствующих сторонах O ₁ отложим отрезки O ₁ A ₁ = О A и O ₁ B ₁ = OB .

2. В плоскости рассмотрим OAA ₁ O _1.

3. В плоскости b , аналогично можно доказать, что

Задача 1. Прямые OB и CD параллельны, а OA и CD – скрещивающиеся прямые. Найдите угол между прямыми OA и CD

Через точку D проведем прямую A ₁ D || AO .

Задача 1. Прямые OB и CD параллельны, а OA и CD – скрещивающиеся прямые. Найдите угол между прямыми OA и CD

Даны параллелограмм ABCD и трапеция ABEK с основанием EK , не лежащие в одной плоскости. Стороны AB = 22,5 см, EK = 27,5 см.

а) Выясните взаимное расположение CD и EK .

б) Найдите периметр трапеции, если известно, что в нее можно вписать окружность.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми.

Цели Образоватедьная Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами; научить находить угол между прямыми в пространстве. Развивающая Развивать у учащихся умение сравнивать и находить аналогии. Воспитательная Воспитывать самостоятельность, творческое отношение к учебному процессу

Расположение 2-х прямых на плоскости а║b пересекаются параллельны a b a b

Ответьте на вопросы по чертежу: Являются ли параллельными прямые АА1 и DD1; АА1 и CC1, и почему? Каково взаимное расположение прямых AA1 и DС?

Скрещивающиеся прямые скрещивающиеся Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости (т.е. не существует плоскости, содержащей эти прямые). a b

Признак скрещивающихся прямых Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, эти прямые скрещивающиеся. Дано: Доказать: A B D C

Признак скрещивающихся прямых Доказательство: Пусть CD и АВ лежат в одной плоскости β. Тогда Плоскости совпадают, но по условию прямая CD пересекает α. Следовательно, плоскости β не существует и прямые АВ и CD скрещиваются. Дано: Доказать: A B B D C

Ответьте на вопросы по чертежу: Каково взаимное расположение прямых AB1 и DС; прямой DС и плоскости AА1 B1В; прямой AB1 и плоскости DD1 C1C?

Теорема о плоскостях, проходящих через скрещивающиеся прямые Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна. Дано: Построить: CD║α Доказать: α - единственная α С В D А

Задача № 34 Дано: DЄ(АВС), АМ=МD, DN=NB, DP=PC, KЄBN Определить взаимное расположение прямых а) ND ? AB б) PK ? BC в) MN ? AB г) MP ? AC д) KN ? AC e) MD ? BC

Задача № 39 Дано: Доказать: Доказательство: 1) Єα по аксиоме А1 2) В¢α, так как по определению скрещивающихся прямых 3) по признаку скр.прямых

полуплоскость полуплоскость граница Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. а

Сонаправленные лучи Два луча ОА иО1А1, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной плоскости с границей ОО1. Два луча ОА иО1А1, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Углы с сонаправленными сторонами A О О1 О2 A1 В2 A2 О3 A3

Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами

Угол между скрещивающимися прямыми Угол между прямыми – это градусная мера, а не геометрическая фигура. Угол между скрещивающимися прямыми АВ и CD определяется как угол между пересекающимися прямыми А1В1║АВ и C1D1║CD (от выбора точки М1 или М2 величина угла φ не зависит)

Ответьте на вопросы по чертежу: Найдите угол между прямыми ВС и СС1 АС и ВС D1C1 и ВС А1В1 и АС

Задача № 44 Дано: ОВ║CD; а) ﮮАОВ=40º б) ﮮАОВ=135º в) ﮮАОВ=90º Найти: угол между ОА и CD

Подготовка к ЕГЭ Решение задач типа В 6

Домашнее задание п.7-9 № 37 № 40 № 93

Подведение итогов: Рефлексия –Что мы с вами повторили на этом уроке? – Что именно привлекло ваше внимание на данном уроке? - Что понравилось? Что вызвало затруднение?

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 608 073 материала в базе

Материал подходит для УМК

2.2. Углы с сонаправленными сторонами

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

21.02.2016 18356
PPTX 538.5 кбайт
2284 скачивания
Рейтинг: 4 из 5
Оцените материал:

Настоящий материал опубликован пользователем Бурчаева Нура Айндиевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Курские власти перевели на дистант школьников в районах на границе с Украиной

Время чтения: 1 минута

Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие

Время чтения: 15 минут

Минтруд предложил упростить направление маткапитала на образование

Время чтения: 1 минута

В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик

Время чтения: 2 минуты

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Время чтения: 1 минута

Отчисленные за рубежом студенты смогут бесплатно учиться в России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Обучающие: организовать деятельность, направленную на формирование понятия угла между скрещивающимися прямыми и закрепление полученных знаний при решении задач.

Развивающие: способствовать развитию пространственного воображения учащихся, умений обосновывать или опровергать выдвигаемые предположения при решении геометрических задач, создать условия для формирования ключевых компетенций учащихся.

Воспитательные: средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.

Тип урока: Изучение нового материала.

2. Актуализация знаний.

4. Изучение нового материала.

6. Первичная проверка понимания темы.

8. Подведение итогов. Рефлексия.

9. Информация о домашнем задании.

I. Организационный момент.

· Приветствие. Психолого-педагогическая настройка учащихся на предстоящую деятельность.

· Проверка домашнего задания. Ответы на возникшие вопросы.

· Мотивация изучения нового материала.

Эпиграфом к нашему уроку послужит народная мудрость:

Жизнь не спросит, что ты учил,
Жизнь спросит, что ты знаешь.

II. Актуализация знаний.

Метод – мозговой штурм

(Вопросы выводятся на презентацию и открываются ответы)

- Какие темы мы прошли на предыдущих уроках?

- Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?

- Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться?

б) быть скрещивающимися?

- Могут ли скрещивающиеся прямые a и b быть параллельными прямой с?

- Даны две скрещивающиеся прямые а и b . Точки А и А₁ лежат на прямой а, точки В и В₁ лежат на прямой b . Как будут расположены прямые АВ и А₁В₁?

- Прямая а скрещивается с прямой b , а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются?

Поисковый метод

Работа с интерактивной доской:

1. Изобразите пары параллельных, пересекающихся и скрещивающихся прямых на готовых моделях многогранников.

2. Найдите пары параллельных, пересекающихся, скрещивающихся прямых на изображении города.

III. Целеполагание.

Метод – эвристическая беседа

Учащимся задаются наводящие вопросы по теме урока. Эти вопросы являются целеполаганием для учащихся.

- Каково взаимное расположение прямых в пространстве?

- Все ли аксиомы и теоремы планиметрии применимы в стереометрии?

- Какую тему мы еще не прошли?

Учащиеся сами формулируют тему урока : "Угол между прямыми"

- Какой из четырех углов, полученных при пересечении двух прямых, мы называем углом между пересекающимися прямыми?

- Чему равен угол между двумя параллельными прямыми?

- Чему равен угол между двумя скрещивающимися прямыми?
Учащиеся формулируют цель и задачи урока.

(Учитель ещё раз проговаривает тему, конкретизирует цель и задачи урока.)

IV. Изучение нового материала.

Наглядно-иллюстративный метод, эвристическая беседа

Использование интерактивной доски.

Расположение прямых в пространстве и угол между ними.

1. Пересекающиеся прямые.

2. Параллельные прямые.

3. Скрещивающиеся прямые.

Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.

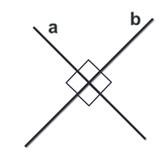
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.

Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.

Угол между двумя параллельными прямыми равен 0°.

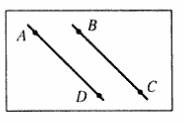
Проговорить метод параллельного переноса при нахождении угла между скрещивающимися прямыми.

Проблемный метод

Использование интерактивной доски.

Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a и b .

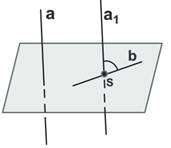
Угол между скрещивающимися прямыми, как и между прямыми одной плоскости, не может быть больше 90°. Две скрещивающиеся прямые, которые образуют угол в 90°, называются перпендикулярными.

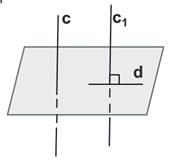
Пусть AB и CD – две скрещивающиеся прямые.

Возьмём произвольную точку М₁ пространства и проведём через неё прямые А₁В₁ и C ₁ D ₁ , соответственно параллельные прямым AB и CD .

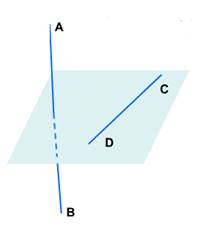
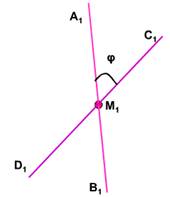
Если угол между прямыми А₁В₁ и C ₁ D ₁ равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ.

Постановка проблемы : Чтобы найти угол между скрещивающимися прямыми AB и CD в качестве точки M ₁ можно взять любую точку пространства?

Учащиеся выдвигают гипотезу : угол между скрещивающимися прямыми не зависит от выбора точки.

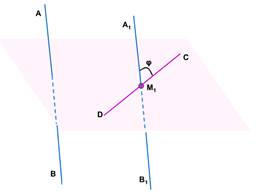
Исследовательский метод.

Учащиеся самостоятельно доказывают, зависит ли угол между скрещивающимися прямыми от выбора точки.

Делают вывод: угол между скрещивающимися прямыми не зависит от выбора точки.

V. Физкультминутка (демонстрация видеоролика)

VI. Первичная проверка понимания темы.

VII. Закрепление нового материала

Работа в парах с самопроверкой. Ответы выводятся по завершении работы. Работа по готовым чертежам.

Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.

а) 90°; б) 45°;

в) 60°; г) 90°;

д) 90°; е) 90°.

Решение задач: №1. Индивидуальная работа.

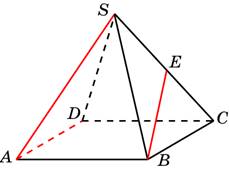
В правильной пирамиде SABCD , все ребра которой равны 1, точка E – середина ребра SC . Найдите угол между прямыми AD и BE .

Искомый угол равен углу CBE .Треугольник SBC – равносторонний.

В E – биссектриса угла 60 ° . Угол CBE равен 30 ° .

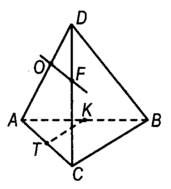
DABC – тетраэдр, точка О и F – середины ребра AD и CD соответственно, отрезок TK – средняя линия треугольника ABC .

a) Чему равен угол между прямыми OF и CB ?

b) Верно ли, что угол между прямыми OF

c) Чему равен угол между прямыми TF и DB ?

Дано: DABC -пирамида, О – середина AD , F – середина CD ,

ТК – средняя линия ∆АВС.

a) В плоскости АВС через точку С проходит прямая АС, параллельная прямой OF (т.к. OF – средняя линия ∆АВС, поэтому АСВ – угол между скрещивающимися прямыми OF и СВ. ∆АВС – правильный, поэтому АСВ=60°.

b) Т.к. OF || AC и TK || CB , то угол между прямыми OF и TK равен углу между прямыми AC и CB , т.е. 60°.

c) Т.к. TF || AD (по свойству средней линии), то ADB =60°.

Решения выводятся на экран для проверки

VIII. Подведение итогов. Рефлексия.

· Что мы узнали нового?

· Справились ли мы с теми задачами, которые были заданы в начале урока?

· Какие задачи мы научились решать?

Выставление отметок за урок.

IX. Информация о домашнем задании.

§4 (стр. 85-89). Уметь объяснить понятие угла между скрещивающимися прямыми. Решить задачи №269, №275. Повторить теорему косинусов .

В этом уроке мы введем понятие сонаправленных лучей. Дадим их определение. А затем докажем теорему о равенстве углов с сонаправленными сторонами.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Углы с сонаправленными сторонами"

· введем понятие сонаправленных лучей;

· дадим определение сонаправленных лучей;

· докажем теорему о равенстве углов с сонаправленными сторонами.

Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.

Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.

Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой.

Определение. Два луча ОА и О₁А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО₁.

Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.

Лучи ОА и O₁A₁, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.

Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Доказательство. Рассмотрим случай, когда углы О и О₁ с соответственно сонаправленными сторонами лежат в разных плоскостях.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОB и

О₁B₁. Т.е. мы имеем два угла АОB и А₁О₁B₁, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А₁О₁B₁.

Отметим на сторонах лучей ОА и O₁A₁ точки А и A₁ так, чтобы отрезки ОА и O₁A₁ были равны. На сторонах лучей ОB и O₁B₁ отметим точки B и B₁ так, чтобы отрезки ОB и O₁B₁ были равны.

Рассмотрим четырехугольник ОАA₁O₁. Так как лучи ОА и O₁A₁ параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА₁О₁ является параллелограммом по признаку параллелограмма. Следовательно, АА₁ параллельно ОО₁ и АА₁ равно ОО₁.

Рассмотрим четырехугольник ОBB₁O₁. Его стороны ОB и O₁B₁ параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB₁O₁ является параллелограммом. Тогда, стороны BB₁ и OO₁ параллельны и равны.

Обратите внимание, мы получили, что прямая AA₁ параллельна прямой OO₁ и прямая BB₁ параллельна прямой OO₁. Тогда по признаку параллельности прямых в пространстве, прямые AA₁ и BB₁ параллельны.

Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA₁ и BB₁ параллельны и равны. А значит, BAA₁B₁ – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A₁B₁ тоже параллельны и равны.

Теперь рассмотрим треугольники АОB и A₁O₁B₁. Стороны ОА и O₁A₁ равны по построению. Стороны ОB и O₁B₁ также равны по построению. Выше мы доказали, что стороны АB и A₁B₁ равны. Значит, треугольники АОB и A₁O₁B₁ равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A₁O₁B₁ равны. Теорема доказана.

Задание. Рассмотрите рисунок и

а) укажите лучи, которые являются сонаправленными;

б) укажите лучи, которые не являются сонаправленными.

Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.

Читайте также: