Производная и ее приложения в электротехнике конспект

Обновлено: 06.07.2024

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y = f ( x ) в точке x 0 – это скорость изменения функции f ( x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y ' , f ' ввёл Ж.Лагранж в 1797г.

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

y = f (x о ) + f ′(x о ) (x – x о )

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , дифференцируемой на интервале , является на этом интервале выпуклым , если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

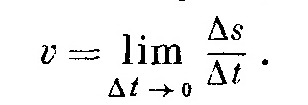
1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов = - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

– мгновенная скорость, м/с
– перемещение тела, м ( если Δt→0 )
Δt – стремящийся к нулю интервал времени, с

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)

Приложение производной в технике: принцип ее работы. Производство, передача и потребление электроэнергии. Геометрический и физический смысл производной. Его применение при исследовании свойств функций Уравнение касательной к графику линейной функции.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	31.10.2017
Размер файла	300,5 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Министерство образования Республики Башкортостан

ГАПОУ Уфимский топливно-энергетический колледж

Использование производной при изучении специальности "Электрические станции сети и системы"

Дисциплина: ''Математика: алгебра, начала математического анализа; геометрия''

Автор проекта: Волков Семён Геннадиевич

1. Производство и передача электроэнергии

2. Использование электроэнергии

2.1 Геометрический смысл производной

2.2 Уравнение касательной

2.3 Физический смысл производной

3. Как решать задачи на физический смысл производной

4. Производная начальный уровень

5. Приложение производной в электроэнергетике

Список использованных источников

Тема индивидуальной проектной работы: Использование производной при изучении моей специальности

Цель работы: Рассмотреть что такое производная в моей специальности Электрические станции сети и системы.

Актуальность работы: В наши дни производная играет одну из самых главных ролей в науке и технике: с помощью дифференциального исчисления находят решение большинства задач в различных областях научного познания.

Количество электричества, протекающее через проводник, начиная с момента времени =0, задается формулой Определить силу тока в конце 6-й секунды.

Для нахождения силы тока используем известные формулы. Сила тока есть производная количества электричества по времени: следовательно, нужно найти производную функции и вычислить ее значение при t=6c. Имеем, откуда при получим (A).

Задача о мгновенной величине тока. Обозначим через q=q(t) количество электричества, протекающее через поперечное сечение проводника за время t.

Пусть Дt - некоторый промежуток времени, Дq = q(t+Дt) - q(t) - количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Дt. Тогда отношениеназывают средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Дq ко времени Дt, при условии, что Дt>0.

Умение дифференцировать позволяет исследовать различные функции. Используя задачи общетехнических и специальных дисциплин, мы формируем понимание глубокой общности в применении математического аппарата к широкому кругу разнообразных явлений природы

Определить, при каком значении тока получается наибольшее значение мощности.

В заключении хотелось бы сказать о том, что энергетика, безусловно, является одним из приоритетных направлений развития общества и государства. При этом развитие цивилизации неразрывно связано с увеличением электропотребления, что, к сожалению, приводит к истощению природных ресурсов. Главнейшей задачей человечества становится предотвращение глобальной проблемы - экологической катастрофы. Ученые всех стран на теории и практике пытаются найти решение. В своих опытах они полагаются на такие дисциплины, как физика, экология, математика (в частности, применение производной).

1. Производство и передача электроэнергии

Электроэнергия производится на электрических станциях зачастую при помощи электромеханических индукционных генераторов. Существует 2 основных вида электростанций -- тепловые электростанции (ТЭС) и гидроэлектрические электростанции (ГЭС) -- различающиеся характером двигателей, которые вращают роторы генераторов.Источником энергии на ТЭС является топливо: мазут, горючие сланцы, нефть, угольная пыль. Роторы электрогенераторов приводятся во вращение при помощи паровых и газовых турбин либо двигателями внутреннего сгорания (ДВС).

Как известно, КПД тепловых двигателей увеличивается с ростом начальной температуры рабочего тела. Поэтому пар, который поступает в турбину, доводят до порядка 550 °С при давлении около 25 МПа. КПД ТЭС достигает 40 %.

Рис. 1 Производство передача и потребление электрической энергии

На тепловых электростанциях (ТЭЦ) большая часть энергии отработанного пара применяется на промышленных предприятиях и для бытовых нужд. КПД ТЭЦ может достигать 60-70 %.

На ГЭС для вращения роторов генераторов применяют потенциальную энергию воды. Роторы приводятся во вращение гидравлическими турбинами.

Производство передача и потребление электрической энергии

Мощность станции зависит от разности уровней воды, которые создаются плотиной (напора), и от массы воды, которая проходит через турбину за 1 секунду (расхода воды).Часть электроэнергии, которая потребляется в России (примерно 10 %), производится на атомных электростанциях (АЭС).

В основном, этот процесс сопровождается существенными потерями, которые связаны с нагревом проводов линий электропередачи током. Согласно закону Джоуля-Ленца энергия, которая расходуется на нагрев проводов, является пропорциональной квадрату силы тока и сопротивлению линии, так что при большой длине линии передача электроэнергии может стать экономически невыгодной. Поэтому нужно уменьшать силу тока, что при заданной передаваемой мощности приводит к необходимости увеличения напряжения. Чем длиннее линия электропередачи, тем выгоднее применять большие напряжения (на некоторых напряжение достигает 500 кВ). Генераторы переменного тока выдают напряжения, которые не могут быть больше 20 кВ (что связано со свойствами используемых изоляционных материалов).

Поэтому на электростанциях ставят повышающие трансформаторы, которые увеличивают напряжение и во столько же раз уменьшают силу тока. Для подачи потребителям электроэнергии необходимого (низкого) напряжения на концах линии электропередачи ставят трансформаторы понижающие. Понижение напряжения обычно производится поэтапно.

2. Использование электроэнергии

Основные потребители электроэнергии:

транспорт (электрическая тяга);

бытовые потребители (освещение жилищ, электроприборы).

Практически вся используемая электроэнергия переходит в механическую энергию. Практически все механизмы в промышленности приводятся в движение электродвигателями.

Примерно треть электроэнергии, которая потребляется промышленностью, используется для технологических целей (электросварка, электрический нагрев и плавление металлов, электролиз и так далее).

2.1 Геометрический смысл производной

Производная в точке x0 равна коэффициенту наклона (тангенсу угла наклона) касательной к графику функции в точке x0: y?(x)=tgб.

Геометрический смысл производной применяется при исследовании свойств функций:

если f?(x0)=tgб>0, то касательная направлена вправо вверх, и функция возрастает;

Сила и импульс по второму закону Ньютона связаны соотношением F=dpdt=p?.

Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока:

В электростатическом поле, изменяющемся только по оси Ox, напряженность и потенциал связаны соотношением

электроэнергия геометрический производная касательная

3. Как решать задачи на физический смысл производной

В задачах на физический смысл производной нужно, зная закон движения материальной точки x(t), найти ее скорость в определенный момент либо определить момент времени, когда достигалась определенная скорость.

Первый шаг -- это вычисление производной в соответствии с правилами дифференцирования.

После этого можно найти скорость в определенный момент времени, подставив соответствующее значение t.

Если же нужно найти момент времени, когда достигалась определенная скорость v0, то нужно решить уравнение x?(t)=v0 относительно t.

Применим этот подход при решении следующей задачи:

Материальная точка движется прямолинейно по закону

(где x -- расстояние от точки отсчета в метрах, t -- время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 96 м/с?

Найдем производную функции x(t):

Остается решить квадратное уравнение

t -- положительное число. Поэтому t=16.

4. Производная начальный уровень

Ось Ox OxOx - это некий уровень нулевой высоты, в жизни мы используем в качестве него уровень моря.

Если конечная точка оказалась ниже начальной, Дf \displaystyle \Delta fДf будет отрицательной - это означает, что мы не поднимаемся, а спускаемся.

Предположим, что на каком-то участке пути при продвижении на 1 11 км дорога поднимается вверх на 1 11 км. Тогда крутизна в этом месте равна 1 11. А если дорога при продвижении на 100 100100 м опустилась на 0,5 0,50,5км? Тогда крутизна равна K=?500м100м=?5K=?500м100м=?5.

А теперь рассмотрим вершину какого-нибудь холма. Если взять начало участка за полкилометра до вершины, а конец - через полкилометра после него, видно, что высота практически одинаковая.

То есть, по нашей логике выходит, что крутизна здесь почти равна нулю, что явно не соответствует действительности. Просто на расстоянии в 1 11 км может очень многое поменяться. Нужно рассматривать более маленькие участки для более адекватной и точной оценки крутизны. Например, если измерять изменение высоты при перемещении на один метр, результат будет намного точнее. Но и этой точности нам может быть недостаточно - ведь если посреди дороги стоит столб, мы его можем просто проскочить.

В реальной жизни измерять расстояние с точностью до милиметра - более чем достаточно. Но математики всегда стремятся к совершенству. Поэтому было придумано понятие бесконечно малого, то есть величина по модулю меньше любого числа, которое только можем назвать. Например, ты скажешь: одна триллионная! Куда уж меньше? А ты подели это число на 2 22 - и будет еще меньше. И так далее. Если хотим написать, что величина x xx бесконечно мала, пишем так:

x>0 \displaystyle x\to 0x>0

5. Приложение производной в электроэнергетике

Производная - одно из фундаментальных понятий математики, это основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).

Еще в древности был решен ряд задач дифференциального исчисления. Архимед, например, разработал способ проведения касательной, применимый для кривых. Само понятие производной возникло в XVII веке в связи с необходимостью решения физических, механических, математических задач, в первую очередь, следующих двух: определение скорости прямолинейного неравномерного движения и построение касательной к произвольной плоской кривой. Первой проблемой занимался великий Исаак Ньютон, второй проблемой - не менее великий Гомтфрид Лейбниц. Независимо друг от друга И.Ньютон и Г.Лейбниц разработали аппарат нахождения производной, которым мы и пользуемся в настоящее время. Благодаря дифференциальному исчислению, был решен целый ряд задач теоретической механики, физики и астрономии. Используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVIII в. Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX в. французский математик О.Коши дал строгое построение дифференциального исчисления на основе понятия предела.

В наши дни производная играет одну из самых главных ролей в науке и технике: с помощью дифференциального исчисления находят решение большинства задач в различных областях научного познания.

Задача о мгновенной величине тока. Обозначим через q = q(t)количество электричества, протекающее через поперечное сечение проводника за время t.

Пусть Дt - некоторый промежуток времени, Дq = q(t+Дt) - q(t) - количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Дt. Тогда отношение мназывают средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Дq ко времени Дt, при условии, что Дt>0.

При изучении механического смысла производной пользуемся механическим истолкованием производной: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е.

Энергетика, безусловно, является одним из приоритетных направлений развития общества и государства. При этом развитие цивилизации неразрывно связано с увеличением электропотребления, что, к сожалению, приводит к истощению природных ресурсов. Главнейшей задачей человечества становится предотвращение глобальной проблемы - экологической катастрофы. Ученые всех стран на теории и практике пытаются найти решение. В своих опытах они полагаются на такие дисциплины, как физика, экология, математика (в частности, применение производной).

Я понял что в наши дни производная играет одну из самых главных ролей в науке и технике: с помощью дифференциального исчисления находят решение большинства задач в различных областях научного познания.

Производная – одно из фундаментальных понятий математики, это основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).Еще в древности был решен ряд задач дифференциального исчисления. Архимед, например, разработал способ проведения касательной, применимый для кривых. Само понятие производной возникло в XVII веке в связи с необходимостью решения физических, механических, математических задач, в первую очередь, следующих двух: определение скорости прямолинейного неравномерного движения и построение касательной к произвольной плоской кривой. Первой проблемой занимался великий Исаак Ньютон, второй проблемой – не менее великий Готфрид Лейбниц. Независимо друг от друга И. Ньютон и Г.Лейбниц разработали аппарат нахождения производной, которым мы и пользуемся в настоящее время. Благодаря дифференциальному исчислению, был решен целый ряд задач теоретической механики, физики и астрономии. Используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVIII в. Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX в. Французский математик О. Коши дал строгое построение дифференциального исчисления на основе понятия предела. В наши дни производная играет одну из самых главных ролей в науке и технике: с помощью дифференциального исчисления находят решение большинства задач в различных областях научного познания.

Задача о мгновенной величине тока. Обозначим через q = q(t) количество электричества, протекающее через поперечное сечение проводника за время t. Пусть Δt – некоторый промежуток времени, Δq = q(t + Δt) – q(t) количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt → 0.

Ускорение движущегося тела представляет собой скорость изменения его скорости, т.е. Точка движется по окружности радиуса 4 м по закону S = 4,5t 3 , где S – путь в метрах, t – время в секундах. Найдем модуль ускорения точки в момент времени Т, когда ν=|ν|=6 м/с.

Производная. Понятие производной является одним из важнейших в курсе математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.

Производной функции y=f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Если у=f(u) и u=φ(x)— дифференцируемые функции своих аргументов, то производная сложной функции у=f(φ(x)) существует и равна произведению производной функции у по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х:

Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.

Таблица формул дифференцирования

10. (a u )’ = a u ln a • u’

11. (e u )’ = e u ln eu’ = e u u’

14. (sin u)’ = cos u • u’

15. (cos u)’ = - sin u • u’

Здесь u и v — дифференцируемые функции от х, а

с - постоянная величина.

Пример 1. Найти производную функции

Решение. Дифференцируем функцию по формулам

Пример 2. Найти производную функции у=sin 3 j и вычислить ее значение при j= p/3.

Решение. Это сложная функция с промежуточным аргументом sinj. Дифференцируем ее по формулам

(u n )' = nu n-1 u', (sin u)' = cos u • u':

f(j) = 3 sin 2 j (sinj)' = 3 sin 2 j cosj.

Вычислим значение производной при j = p/З:

f(p/3) = 3sin 2 (p/3) cos(p/3)=3(Ö3/2) 2 •(1/2)=3•(3/4) • (1/2)=9/8.

Пример 3. Найти производную функции

Решение. Сначала преобразуем функцию, используя свойства логарифмов: t

Геометрический смысл производной. Производная функции у =f(x) представляет собой угловой коэффициент касательной, проведенной к графику функции в любой его точке.

Угловой коэффициент касательной, проведенной к графику функции y=f(х) в точке A(а;b), равен значению производной функции при х = а:

Уравнение касательной, проведенной к графику функции в этой точке, имеет вид

у— b=k (х -а), где k=f’(a).

Пример 4.Составить уравнение касательной, проведенной к графику функции в точке с абсциссой х=2.

Решение. Сначала найдем ординату точки касания А (2;у). Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т. е.

Уравнение касательной, проведенной к кривой в точке А(2;2), имеет вид у - 2 = k(x - 2). Для нахождения углового коэффициента касательной найдем производную:

Угловой коэффициент касательной равен значению производной функции при х = 2:

Уравнение касательной таково:

у - 2 = - (х - 2), или у - 2 = -х + 2, т. е. х + у - 4 = 0.

Физический смысл производной. Если тело движется по прямой по закону s = s (t), то производная пути s по времени t равна скорости движения тела в данный момент времени t:

Быстрота протекания физических, химических и других процессов также выражается с помощью производной.

Производная функции у=f(х) равна скорости изменения этой функции при данном значении аргумента х:

Пример 5. Закон движения точки по прямой задан формулой s=t 2 +3t+5. В какие моменты времени t скорость движения точки равна нулю?

Решение. Скорость прямолинейного движения точки равна производной пути s по времени t:

v (t) = s' = 3 t 2 - 6t + 3; v (t) =0,З t 2 - 6t + 3 = 0,

t 2 - 2t + 1 = 0, (t — 1) 2 = 0, откуда t = 1.

Вторая производная. Производной второго порядка (или второй производной) функции называется производная от первой производной у' =f' (х):

у" = (у’)' или f" (х) = (f' (х))'.

Пример 6. Найти вторую производную функции f(x)=tg x.

Решение. Сначала по формуле найдем первую производную:

Дифференцируя еще раз по формулам (u n )’=nu n -1 u’, сos u)’=-sin u*u’, найдем вторую производную:

Физический смысл второй производной. Если тело движется прямолинейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:

Пример 7. Точка движется по прямой по закону s=t 3 -5t 2 +8t+2. (s - в метрах, t - в секундах). Найти ускорение движения точки в конце второй секунды.

Решение. Сначала найдем производную пути s по времени t:

s' = 3 t 2 - 10 t + 8.

Ускорение прямолинейного движения точки равно второй производной пути s по времени t:

а (t) = s" = 6 t - 10, а(2) = 6 • 2 - 10 = 12 - 10 = 2.

Ускорение движения точки в конце второй секунды равно 2 м/с 2 .

Приложения производной к исследованию функций.Дифференцируемая функция у=f (х) возрастает на промежутке ]а, b[, если ее производная положительна в каждой точке этого промежутка.

Дифференцируемая функция у=f(x) убывает на промежутке]а; b[, если ее производная отрицательна в каждой точке этого промежутка.

Функция y=f(x) имеет максимум в точке х = x₁ (рис. 38), если для всех значений х, достаточно близких к x₁, выполняется неравенство f(х) f(х₂); х = х₂ - точка минимума; у_ma_х = f(х₂) - минимум функции.

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - экстремальными.

Точки, в которых производная функции обращается в нуль, называются критическими, точками I рода.

Первое достаточное условие существования экстремума функции. Если при переходе через критическую точку I рода х=х₀ производная функции y=f(х) меняет знак, то х=х₀ - точка

При этом если производная меняет знак с плюса на минус, то х=х₀= - точка максимума, а у_m_ах =f(х₀). Если же производная меняет знак с минуса на плюс, то х= х₀ - точка минимума, a у_min =f(х₀)

Второе достаточное условие существования экстремума функции. Если в точке х = х₀ первая производная функции у=f(x) обращается в нуль, а вторая производная отлична от нуля, то х=х₀ - точка экстремума.

При этом если вторая производная в этой точке положительна (f" (х₀)>0), то х=х₀ - точка минимума; если вторая производная в этой точке отрицательна (f"(х₀) 3 - Зх.

Решение 1. Областью определения функции служит множество всех действительных чисел, т. е. х = R.

2. Находим точки пересечения графика функции с осями координат:


рис.42.	рис. 43.

3. Находим экстремумы функции. Для этого сначала найдем производную у' = Зх 2 - 3. Затем найдем критические точки I рода: у' = 0,Зх 2 - 3=0, х 2 = 1, х₁= 1, х₂ = -1. Отметим эти точки на числовой прямой (рис. 43). Исследуем знак производной в каждом интервале; у'(-2) > 0, у' (0) 0. Функция возрастает при хÎ] -¥,-1[U]1,+¥[и убывает при хÎ] –1,1[. Итак, х= -1 — точка максимума; у_ma_х = у(-1)=(-1) 3 -3(-1)=-1+3=2; х=1 — точка минимума; y_min = у (1) = 1 3 —3*1=1-3=-2.

4. Находим направление вогнутости и точки перегиба графика функции. Для этого сначала найдем вторую производную у" = 6х, а затем критические точки II рода: у" =0,6х=0, х = 0. Отметим эту точку на числовой прямой (рис. 44). Исследуем знак второй производной в каждом интервале:


рис. 44	рис. 45

Таким образом, график является выпуклым при хÎ] -¥,0[ и вогнутым при хÎ] 0, + ¥ [; х = 0 — абсцисса точки перегиба, y_т.п= у(0) = 0; О (0,0) - точка перегиба графика функции.

Отметим все полученные точки в системе координат и соединим их плавной кривой (рис. 45).

Для уточнения графика функции можно найти дополнительные точки, используя уравнение функции: у(-2)= -2, у (2) =2.

Вопросы для самопроверки

1. Дайте определение производной функции.

2. В чем состоит геометрический смысл производной?

3. В чем состоит физический смысл производной?

4. Дайте определение второй производной функции.

5. В чем состоит физический смысл второй производной?

6. Напишите все формулы дифференцирования.

7. Как найти промежутки возрастания и убывания функции?

8. Как найти точки экстремума и экстремумы функции?

9. Как найти промежутки выпуклости и вогнутости кривой?

10. Как найти точки перегиба кривой?

11. Найдите производные функций: а) у = In tg (х/2);

б) у = cos 2 Öx; в) f(x)=(x+1)2х-1.

12. Составьте уравнение касательной к кривой у = х 2 — 4х в точке с абсциссой х = 1.

13. Прямолинейное движение точки задано уравнением

(s - в метрах, t - в секундах). Найдите скорость и ускорение движения точки в конце второй секунды,

14. Какой из прямоугольников с периметром, равным 48см, имеет наибольшую площадь?

15. Число 66 представьте в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было наибольшим.

Ответы. 11. a) cosec х; б) в)

12. 2х+у+1=0. 13. 3 м/с, 2 м/с 2 . 14. Квадрат со стороной 12 см. 15. 33 и 33.

Решение. Находим производную данной функции, используя формулы

Умножив производную на дифференциал аргумента, получим дифференциал:

Пример 2. Вычислить значение дифференциала функции n = In sin 2j при j = p/8, Dj = 0,02.

Решение: Дифференциал функции вычисляем по формуле dv = v' (j) dj.

Прежде чем применить эту формулу, используя равенства

(sin u)’ = cos u , u’, (си)’=си’, находим производную функции и ее значение при j = p/8:

Понятие о дифференциальном уравнении. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).

Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения F (х, у, у') = 0.

Общим решением дифференциального уравнения первого порядка называется функция у = j(х, С) от х и произвольной постоянной С, обращающая это уравнение в тождество.

Общее решение, записанное в неявном виде Ф (х, у. С) =0, называется общим интегралом.

Частным решением уравнения F (х, у, у') = 0 называется решение, полученное из общего решения при фиксированном значении С: у =j(х, С_о), где С_о - фиксированное число.

Частным интегралом уравнения F(x, у, у') = 0 называется интеграл, полученный из общего интеграла при фиксированном значении С: Ф (х, у, С_о) = 0.

График любого частного решения дифференциального уравнения F (х, у, у') = 0 называется интегральной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра С.

Пример 1. Составить уравнение кривой y=f(x), если угловой коэффициент касательной, проведенной в любой точке кривой, равен 2х.

Решение. Так как на основании геометрического смысла производной у' = k_кас, то получим дифференциальное уравнение первого порядка:

Чтобы найти, искомую функцию у=f(х), надо проинтегрировать обе части уравнения: òdy = ò 2xdx. Отсюда получим общее решение дифференциального уравнения:

у=х 2 +С. Геометрически это решение представляет собой семейство парабол (рис. 55) с вершиной на оси Оу, симметричных относительно этой оси.

Чтобы из общего решения выделить частное решение, надо задать начальные условия. Пусть у = -1 при х=1; тогда общее решение примет вид -1 = 1 + С, откуда С = - 2. Геометрически частное решение у = х 2 - 2 представляет собой параболу, проходящую через точку (1; -1) (рис. 55).

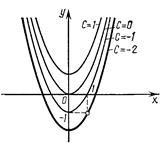
Дифференциальные уравнения с разделяющимися переменными. Общий вид такого уравнения

где Х (х), Х₁(х) — функции только от х, Y(у), Y₁(у)—функции только от у.

Поделив обе части уравнения на произведение X₁(x)•Y(у)¹0, получим уравнение с разделенными переменными:

Читайте также: