Признак подобия треугольников по двум сторонам и углу между ними конспект

Обновлено: 05.07.2024

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 35. Второй и третий признаки
подобия треугольников

Основные дидактические цели урока: рассмотреть второй и третий признаки подобия треугольников; показать применение второго и третьего признаков подобия треугольников при решении задач.

Ход урока

I. Организационный момент.

Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся

Решить задачу № 57 (самостоятельно с последующим обсуждением решения).

Докажите, что ΔABF ~ ΔCDF.
Чему равен коэффициент подобия треугольников ABF и CDF?
Найдите отношение сторон BF и DF.
Чему равно значение DF?

Решение задач по готовым чертежам (самостоятельно). (В тетрадях записать краткое решение.)

1) Дано: ∠N = ∠A, ВС = 12 см, MN = 6 см, CN = 4 см (рис. 7.27). Найти: АС.
2) Дано: ВС ⊥ АС, EF ⊥ AB, ВС = 12 см, EF = 6 см, АЕ = 10 см (рис. 7.28). Найти: АВ.
3) Дано: ∠3 = ∠1 + ∠2, CD = 4 см, ВС = 9 см (рис. 7.29). Найти: АС.

III. Работа по теме урока

Формулировка темы урока.

Сформулируйте первый признак равенства треугольников.
Существуют ли еще какие-либо признаки подобия треугольников?

Сформулировать другие признаки подобия треугольников (работа в группах).
Доказать второй и третий признаки подобия треугольников.

Второй признак подобия треугольников

Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

(Учащиеся записывают в тетрадях план-конспект доказательства теоремы.)

План-конспект доказательства теоремы

Составить план-конспект доказательства третьего признака подобия треугольников. (Учитель делит класс на группы. На обсуждение дается 5 мин. Далее заслушивают представителей групп, в обсуждении решения участвует весь класс.)

Третий признак подобия треугольников

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

План-конспект доказательства теоремы

IV. Закрепление изученного материала

1. Работа в рабочих тетрадях.

Решить задачи № 59, 60 (работа в парах). (Учитель контролирует работу менее подготовленных учащихся и по мере необходимости оказывает индивидуальную помощь.)

Задача № 59. Наводящие вопросы.

Каким является ∠C для треугольников АВС и MNC?
Чему равно отношение сторон, заключающих этот угол (АС : CN и ВС : СМ)?
Что можно сказать о сторонах АС и ВС треугольника АВС и сторонах CN и СМ треугольника MNC?
Какой признак подобия треугольников был применен при доказательстве подобия треугольников MNC и АВС?

Задача № 60. Наводящие вопросы.

Чему равно отношение сторон MN и CD, МР и СЕ, NP и DE треугольников MNP и CD ЕР
Что можно сказать о сторонах треугольников MNP и CDE?
Укажите признак, на основании которого треугольники MNP и CDE подобны.

(Учащиеся, успешно справившиеся с решением задач, решают дополнительные задачи.)

2. Решить дополнительные задачи.

2) В треугольнике АВС АВ = 4, ВС = 6, АС = 7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ = 5,25, ME = 4,5, АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что ΔАРВ равнобедренный.

V. Рефлексия учебной деятельности

Сформулируйте второй (третий) признак подобия треугольников.
Две стороны одного треугольника пропорциональны двум сторонам другого. В каком случае данные треугольники будут подобны?
Подобны ли равнобедренные треугольники, если у них углы между боковыми сторонами равны?
Подобны ли равнобедренные треугольники, если боковая сторона и основание одного из них пропорциональны боковой стороне и основанию другого?
Могут ли быть подобными прямоугольные треугольники, если катеты одного из них пропорциональны катетам другого?

Домашнее задание

П. 62, 63, вопросы 6, 7 (учебник, с. 158, 159).
Решить задачи № 559, 560 (б), 561.
Решить дополнительную задачу.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников.

I. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

III. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Определение 1. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Определение 2. Сходственными называются стороны подобных треугольников, лежащих напротив равных углов.

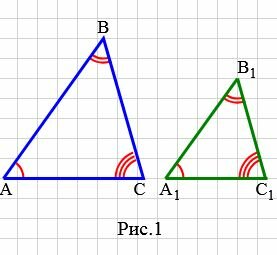На рисунке 1 углы треугольников \( \small ABC \) и \( \small A_1B_1C_1 \) соответственно равны:

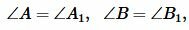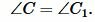(1)

Тогда стороны \( \small AB \) и \( \small A_1B_1 \), \( \small BC \) и \( \small B_1C_1 \), \( \small AC \) и \( \small A_1C_1 \) называются сходственными.

Определение 1 можно понимать так: два треугольника подобны, если для них можно ввести обозначения и (Рис.1) так, что

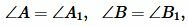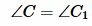Если два треугольника и подобны, то это обозначают так:

Коэффициент подобия треугольников

Коэффициентом подобия треугольников k − это число, равное отношению сходственных сторон (см. формулу (2)).

Перый признак подобия треугольников

Теорема 1. Если два угла одного треугольника соответсвенно равны двум углам другого треугольника, то такие треугольники подобны.

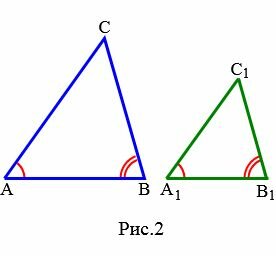Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.2).

Поскольку сумма углов треугольника равна 180°, то можно записать:

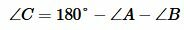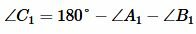и, так как , , получим:

Таким образом углы треугольника соответственно равны углам треугольника . Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).

Площади треугольников и по двум сторонам и углу между ними можно вычислить формулами:

Из (3) и (4), и из следует:

С другой стороны:

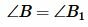
Из (6) и (7), и из следует:

Левые части уравнения (5) и (8) равны. Следовательно равны и правые части:

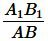
Умножая левую и правую части уравнения (9) на , получим:

Продолжая аналогичные рассуждения, получим:

Сравнивая (8) и (11), получим:

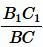
Умножая левую и правую части уравнения (12) на , получим:

Из (10) и (13), получим:

То есть стороны треугольника пропорциональны сходственным сторонам треугольника . Что и требовалось доказать.

Второй признак подобия треугольников

Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.

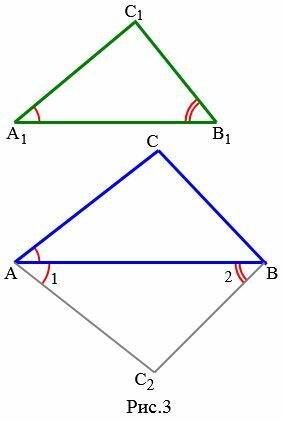Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.3).

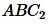
Рассмотрим треугольник у которого

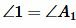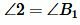(15)

Из условия (15) следует, что треугольники и подобны (по первому признаку подобия треугольников). Следовательно:

Но по условию теоремы . Поэтому . Треугольники и равны по двум сторонам и углу между ними (сторона AB общая, , (поскольку и )). Следовательно и поскольку , то .

Получили, что и . Тогда по первому признаку подобия треугольников .

Третий признак подобия треугольников

Теорема 3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть стороны треугольников пропорциональны:

Докажем, что . Рассотрим треугольник у которого , (Рис.3). Треугольники и подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:

Сравнивая равенства (16) и (17) получаем: , .

Из этих рассуждений следует, что треугольники и равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда , а поскольку , то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .

Отношение площадей подобных треугольников

Теорема 4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Пусть треугольники и подобны. Тогда

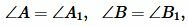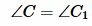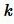
где -коэффициент подобия.

Читайте также: