Приращение аргумента и приращение функции конспект урока

Обновлено: 07.07.2024

Оборудование: учебник А.Н. Колмогорова “Алгебра и начала анализа” 10-11 кл.; мультимедийный проектор и экран.

I. Организационный момент:

Взаимное приветствие учителя и учащихся, проверка готовности учащихся к уроку.

II. Анализ контрольной работы по теме: “Решение тригонометрических уравнений и неравенств”/

III. Актуализация знаний:

Формула периметра прямоугольника;
Формула площади прямоугольника;
Определение функции, определение тангенса угла;
Как найти значение функции в данной точке?

Пример: Найти значение функции f(x) = x 2 + 2x в точке x₀ = -3.

Решение: f(x₀) = f(-3) = (-3) 2 + 2∙(-3) = 9 - 6 = 3

Ответ: f(-3) = 3

IV. Изучение нового материала:

Часто нас интересует не значение какой-либо величины, а ее изменение.

Например: Дан график функции у = 4 -х 2

Разность х₂ – х₁ = 2 - 1 = 1; ∆x =1

f (1) = 3; f(2) = 0; f(2) – f(1) = 0 - 3 = -3

При сравнении значений функции f в некоторой фиксированной точке х₀ со значениями этой функции в различных точках х, лежащих в окрестности х₀, удобно выражать разность f(x) - f(x₀) через разность х - х₀, пользуясь понятиями “приращение функции” и “приращение аргумента”.

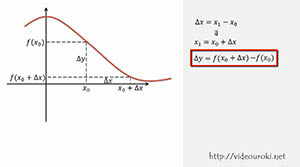
Рассмотрим функцию у = f(x). Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х₀. Разность х - х₀ называется приращением независимой переменной (или приращением аргумента) в точке х₀ и обозначается х. Таким образом, х = х - х₀, откуда следует, что х = х₀ +х.

Говорят также, что первоначальное значение аргумента х₀ получило приращение х. Вследствие этого значение функции f изменится на величину f(x) - f(x₀) = f(х₀ + х) – f(x₀).

Эта разность называется приращением функции f в точке х₀, соответствующим приращению х, и обозначается f, т. е. по определению

Обратите внимание: при фиксированном значении х₀ приращение f есть функция от х. (Слайд 4.)

Найти приращение аргумента и приращение функции в точке х₀, если

Рассмотрим график функции у = f (x). Геометрический смысл приращения функции можно понять, рассмотрев рисунок. (Слайд 6.) Прямую l, проходящую через любые две точки графика функции f, называют секущей к графику f. Уравнение прямой на плоскости имеет вид у = кх + в. Угловой коэффициент k секущей, проходящей через точки (х₀; f(x₀) и (х; f(x)), равен tga. ABC – прямоугольный.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Приращение аргумента, приращение функции"

· познакомиться с понятием непрерывной функции;

· познакомиться с понятием предел функции в точке;

· рассмотреть примеры использования данных понятий для решения задач.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Не всегда нам надо знать точные значения тех или иных параметров. Иногда нам достаточно знать, как они изменяются. Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на сколько именно изменилась температура воздуха, а нам важно похолодало или потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а важно определить разгоняется автомобиль или тормозит.

Причём, если на улице потеплело, то изменения будут со знаком плюс и наоборот если похолодало, то изменения будут со знаком минус.

Если автомобиль разгоняется, то изменения будут со знаком плюс, если тормозит – то со знаком минус.

Для описания таких изменений было введено понятие приращение.

Определение.

Пусть функция y = f(x) определена в точках x₀ и x₁. Разность x₁ – x₀ называют приращением аргумента, а разность f(x₁) – f(x₀) называют приращением функции.

Приращение аргумента обозначают так:

Приращение функции обозначают так:

Давайте рассмотрим, что же такое приращение аргумента и функции на графике.

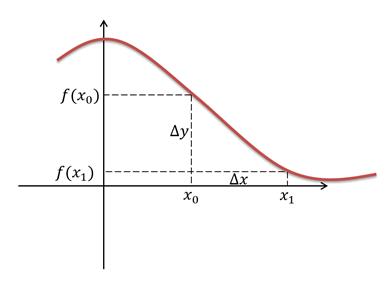
Рассмотрим ещё один пример.

Давайте вспомним определение непрерывной функции, которое мы формулировали ранее.

Определение непрерывности функции в точке x = a выглядит так:

Определение непрерывности функции в точке можно записать так:

Когда мы вводили определение непрерывной функции, то мы говорили, что функция непрерывна на промежутке X, если она непрерывна в каждой точке промежутка. Давайте уточним, что означает непрерывность функции в концевых точках промежутка, например, как понимать непрерывность функции в точках a и b отрезка [a; b].

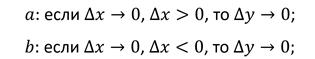
Давайте изобразим график линейной функции. Отметим приращение аргумента и функции. И найдём чему равно отношение приращения аргумента к приращению функции.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Учитель: Манахова Е.А.

Предмет: математика

Класс: 10

Тип урока: урок получения нового знания .

образовательные: сформировать понятия приращения функции и приращения аргумента, секущей, геометрического смысла приращения функции; показать применение данных понятий при решении задач.

развивающие: развитие вычислительных навыков, умений логически и аргументированно рассуждать, обобщать и абстрагировать.

воспитательные: воспитание познавательного интереса к предмету.

Оборудование: учебник; компьютер, проектор и экран .

1.Организационный момент

1) Взаимное приветствие преподавателя и обучающихся, проверка готовности обучающихся к уроку.

2.Подготовка к восприятию нового материала

(устная работа с целью актуализации знаний):

Как найти значение функции в данной точке?

Пример: (Слайд 3)

Найти значение функции f(x) = x 2 + 2x в точке x ₀ = -3.

Решение: f(x ₀ ) = f(-3) = (-3) 2 + 2∙(-3) = 9 - 6 = 3

3) Итак, мы поработали устно и вспомнили некоторые теоретические сведения, которые нам будут нужны при изучении нового материала. А теперь мы выясним, что же такое приращение аргумента и приращение функции.

2. Изучение нового материала:

1) Часто нас интересует не значение какой-либо величины, а ее изменение. Например: как быстро изменяется температура, как быстро дорожают цены на билеты и так далее…

Давайте рассмотрим с Вами основные понятия которые относятся к приращению функции .

(работа с раздаточным материалом)

Например: Дан график функции у = 4 -х 2 (Слайд 4 )

По графику найти значение функции в точке х ₁ = 1 и

Разность х ₂ – х ₁ = 2 - 1 = 1; ∆x =1

f (1) = 3; f(2) = 0; f(2) – f(1) = 0 - 3 = -3

2). В приведенном примере мы не только вычислили значения функции f(x) в некоторых точках, но и оценили изменения ∆f этой функции при заданных изменениях аргумента ∆х.

При сравнении значений функции f в некоторой фиксированной точке х ₀ со значениями этой функции в различных точках х, лежащих в окрестности х ₀ , удобно выражать разность f(x) - f(x ₀ ) через разность х-х ₀ , пользуясь понятиями “приращение функции” и “приращение аргумента”.

Рассмотрим функцию у = f(x). Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х ₀ . Разность х - х ₀ называется приращением независимой переменной (или приращением аргумента) в точке х ₀ и обозначается ∆х. Таким образом, ∆х= х -х ₀ , откуда следует, что х = х ₀ +∆х. ( Слайд 5)

Говорят также, что первоначальное значение аргумента х ₀ получило приращение ∆х. Вследствие этого значение функции f изменится на величину f(x) - f(x ₀ ) = f(х ₀ + х)– f(x ₀ ).

Эта разность называется приращением функции f в точке х ₀ , соответствующим приращению ∆х, и обозначается ∆f, т. е. по определению

Обратите внимание: при фиксированном значении х ₀ приращение ∆f есть функция от ∆х.

2) Что такое приращение аргумента?

Что такое приращение функции? ( Слайд6 )

Приращением аргумента функции называется величина, равная разности между конечным и начальным значением аргумента: ∆ x = x -х ₀

Приращением функции называется величина, равная разности между конечным и начальным значением функции ∆f =f(x) - f(x ₀ ) = f(х ₀ + х)– f(x ₀ ).

Пример 1. Найти приращение функции y = x 3 при переходе от х ₀ =1,2 к точке х=2,5 (Слайд 7)

Решение: ∆ x =2,5-1,2=1,3, ∆f=2,5 2 -1,2 2 =6,25-1,44= 4,81

Пример 2. Найти приращение аргумента и приращение функции в точке х ₀ , если f ( x )= x 2 , если х ₀ = 2, х=1,9. (Слайд 8)

Решение: ∆ x =1,9-2=-0,1, ∆f=1,9 2 -2 2 =3,61-4= -0,39

Вывод: Приращение функции может быть как положительным так и отрицательным.

Теперь выясним геометрический смысл приращения аргумента, приращения функции. (Слайд 9.)

Рассмотрим график функции у = f (x). Геометрический смысл приращения функции можно понять, рассмотрев рисунок. Прямую l, проходящую через любые две точки графика функции f, называют секущей к графику f. Уравнение прямой на плоскости имеет вид у = кх + b . Угловой коэффициент k секущей, проходящей через точки (х ₀ ; f(x ₀ ) и (х; f(x)), равен tga. ∆ABC – прямоугольный.

Пример 3. Найти угловой коэффициент секущей к графику функции f ( x ) = , проходящей через точки с данными абсциссами х ₁ и х ₂ . Какой угол (острый или тупой) образует секущая с осью Ох, если f ( x ) = x 2 ; x ₁ = 0; x ₂ = 1 (Слайд 10)

Δx = 1 – 0 = 1; Δf = f(1) - f(0) = · 1 2 - · 0 2 =

k = tgα = > 0, значит α – острый

Ответ: tgα = ; α - острый

5) Итак, мы выяснили что такое приращение аргумента и приращение функции и в чём состоит их геометрический смысл. Теперь мы научимся применять данные определения при решении задач.

3.Закрепление изученного материала

1. Решение задач у доски преподавателем.

а) Найдите приращение функции f в точке х ₀ , если

f ( x ) = 3 x +1 x ₀ = 5 ∆ x = 0, 01.

Решение: х=х ₀ +∆ x , х= 5+0,01=5,01

f( х ₀ ) = f(5)=3·5+1=16 ; f (x)=f(5 ,0 1) = 3·5,01+1=1 6 ,03

Δf = f ( x ) - f ( x ₀ ); Δf = 16,03-16=0,03 Ответ: 0,03 (Слайд 11)

б) Найти приращение функции y = f ( x ) при переходе от точки х к точке х+ ∆ x , если f ( x )= х 2 .

Решение: Δf = f ( x ) - f ( x ₀ )= f (х+ ∆ x )- f ( x )= (х+ ∆ x ) 2 - x 2 = x 2 +2 x ∆ x +∆ x 2 - x 2 =2 x ∆ x +∆ x 2

Ответ: 2 x ∆ x +∆ x 2 (Слайд 12)

5. Проверка усвоения материала.

Самостоятельная работа (Слайд 13)

1 вариант № 26.20(а), 26.22 (а), 26.24 (а)

2 вариант №26.20(б), 26.22(б), 26.24(б)

( 1 вар- №26.20 0,4 №26.22 0,2; №26.24 3 ∆ x

2 вар- №26.20 2,8 №26.22 - 0,1; №26.24 -2х ∆ x - (∆ x ) 2 )

6. Подведение итогов урока.

Домашнее задание: П.26, №26.20-26.21(вг), 26.22(вг), 26.24 (вг)

Тип урока: формирование новых понятий.

Метод обучения: обучающая беседа.

Оборудование: учебник А.Н. Колмогорова “Алгебра и начала анализа” 10-11 кл.;

Дата проведения: 29 января 2018 года

Формирование понятий приращения функции и приращения аргумента, секущей, геометрического смысла приращения функции;

Развитие вычислительных навыков;

Воспитание познавательного интереса к предмету.

Тип урока: формирование новых понятий.

Метод обучения: обучающая беседа.

Оборудование: учебник А.Н. Колмогорова “Алгебра и начала анализа” 10-11 кл.;

I. Организационный момент:

Взаимное приветствие учителя и учащихся, проверка готовности учащихся к уроку.

Познакомимся с такими понятиями как приращение функции и приращение аргумента, рассмотрим геометрический смысл приращения функции;

Продолжим работу над развитием вычислительных навыков;

1. Что мы называем функцией, какие вы функции знаете?

2. Что мы называем аргументом, значением функции.

3. Можно ли задать площадь квадрата как функцию

4. Как найти значение функции в данной точке?

Пример: Найти значение функции f(x) = x 2 + 2x в точке x₀= -3.

Решение: f(x₀) = f(-3) = (-3) 2 + 2∙(-3) = 9 - 6 = 3

Ответ: f(-3) = 3

5. Определение тангенса угла;

IV. Изучение нового материала:

Часто нас интересует не значение какой-либо величины, а ее изменение. Например, как изменяется температура, как быстро растет цена на бензин. Из курса физики мы знаем, что работа есть изменение энергии, а средняя скорость есть отношение перемещения к промежутку времени, за которое было совершено перемещение.

Давайте рассмотрим график функции у = 4 -х 2

По графику найти значение функции в точке х₁= 1 и х₂= 2.

у₁= f (1) = 3; у₂= f(2) = 0;

Найдем изменение аргумента

Разность х₂– х₁= 2 - 1 = 1 пишут ∆x =1

Найдем изменение значений функции

Разность f(2) – f(1) = 0 - 3 = -3 пишут f = -3

В этом примере мы вычислили значения функции f(x) в точках х₁= 1 и х₂= 2, и оценили изменения f этой функции при заданных изменениях аргумента х.

Часто приходится сравнивать значение функции в некоторой фиксированной т.х₀ и значение функции в различных точках х, расположенных в окрестности х_0,.При этом удобно выражать разность f(x) - f(x₀) через разность х - х₀, пользуясь понятиями “приращение функции” и “приращение аргумента”.

Рассмотрим функцию у = f(x).

х₀ – фиксированная точка

х – произвольная точка

Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х₀.

Разность х - х₀ называется приращением независимой переменной (или приращением аргумента) в точке х₀ и обозначается х, т.е. х = х - х₀, откуда следует, что х = х₀ +х.

поэтому говорят, что первоначальное значение аргумента х₀ получило приращение х.

Вследствие этого значение функции f изменится на величину f(x) - f(x₀) = f(х₀+х) – f(x₀).

Эта разность называется приращением функции f в точке х₀, соответствующим приращению х, и обозначается f, (дельта эф), т. е. по определению

∆f = f (x) - f(x₀) или f = f (х₀+х) – f(x_0), откуда f (х₀ + х) = f(x₀) + f.

Обратите внимание: при фиксированном значении х₀ приращение f есть функция от х, т.е. f (х₀ + х) = f(x₀) + f.

Найти приращение аргумента и приращение функции в точке х₀, если

Решение:

Обсудим геометрический смысл введенных понятий приращений аргумента и функции, его можно понять, рассмотрев рисунок.

Читайте также: