Площадь сферы 11 класс конспект урока

Обновлено: 05.07.2024

2 ученика доказывают у доски свойство и признак касательной плоскости к сфере.

а) доказательства прямой и обратной теорем о касательной плоскости;

б) решение домашних задач.

(см. решение урок № 24).

Задача № 591. Дано: сфера с центром в точке О касается двугранного угла в 120°, расстояние от точки О до ребра угла а (рис. 1).

Найти: АВ, R сферы.

Решение: Рассмотрим сечение плоскостью, проходящей через центр шара О и перпендикулярной ребру двугранного угла MN.

Эта плоскость будет перпендикулярна и касательным к сфере плоскостями α и β. Проведем ОВ ⊥ α, ОА ⊥ β. ОВ = ОА = R.

ОА ⊥ β, AC ⊥ MN по построению, ОС ⊥ MN по теореме о трех перпендикулярах. ОС = а - расстояние от центра сферы до ребра MN.

ΔОВС = ΔОАС (ОВ = ОА = R, ОС - общая) значит, ОС – биссектриса ∠ACB = 120°, значит, ∠OCA = 60°. В ΔОСА: OA = R = 0 sin 60° = ΔАОВ - равнобедренный, (ОВ = ОА = R) ∠AOB = 60°, значит, ∠OBA = ∠OAB = 60°, то есть ΔАОВ - равносторонний АВ = ОА = расстояние между точками касания.

(Ответ: , .)

а) работа по карточке сфера задана уравнением: x2 + y2 + z2 + 2y - 4z = 4. Найдите координаты центра и радиус сферы.

x2 + y2 + z2 + 2y - 4z = 4 выделим квадрат двучлена: х2 + у2 + 2у + 1 - 1 + z2 - 4z + 4 - 4 = 4, х2 + (у + 1)2 + (z - 2)2 = 9 центр окружности С(0; -1; 2), радиус R = 3.

б) устный опрос учащихся:

1) Что мы называем сферой?

Поверхность, состоящая из множества точек, равноудаленных от центра.

2) Что называется шаром?

Часть пространства ограниченная сферой.

3) взаимные расположения плоскости и сферы:

- нет общих точек;

- пересекаются по окружности;

- касаются (имеют одну общую точку)

4) касательная плоскость к сфере

Плоскость, имеющая со сферой только одну общую точку.

5) уравнение сферы

(x - х0)2 + (у - у0)2 + (z - z0)2 = R.

в) работа с чертежом (устно) (рис. 2)

АВ = 6 см, ВС = 8 см, АС = 10 см.

ΔABC прямоугольный, так как 102 = 82 + 62, т.е. ∠CBA = 90°, значит, ∠CBA опирается на диаметр сечения СА, тогда радиус, сечения r = 10 : 2 = 5 (см), К - центр круга, значит, по теореме Пифагора.

г) рассмотрим вопросы из учебника:

№ 7. Точка А и В принадлежат шару. Принадлежит ли этому шару любая точка отрезка АВ?

№ 8. Могут ли все вершины прямоугольного треугольника с катетами 4 см и 2√2 см лежать на сфере радиуса √5?

- диаметр сечения, на который опирается прямой угол, значит, радиус такого сечения что больше радиуса сферы, таким образом, нет, не могут.

№ 9. Могут ли две сферы с общим центром и с неравными радиусами иметь общую касательную плоскость?

III. Изучение нового материала

1) Рассмотрим рисунок 156 учебника.

Многогранник называется описанным, если сфера касается всех его граней. Сфера будет вписанной в этой многогранник.

2) Площадью сферы будем называть предел последовательности площадей поверхностей, описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.

IV. Закрепление изученного материал.

пропорциональны.

V. Самостоятельная работа (обучающего характера) (10 мин)

Сечение шара площадью S = 16π см2 находится на расстоянии 3 см от центра шара.

Найдите площадь его поверхности.

Дано: шар с центром в точке О, Sсеч. = 16π см2, расстояние от точки О до сечения 3 см (рис. 3).

Решение: значит, Рассмотрим ΔОАВ OA = d - расстояние, значит, ∠A = 90°. (Ответ: 100π см2.)

К сфере с S = 64π см2 проведена касательная плоскость. Кротчайшее расстояние от точки А, лежащей в этой плоскости, до данной сферы равно 1 см.

Найти расстояние от точки А до точки касания сферы с плоскостью.

Дано: сфера с центром в точке О, α - касательная плоскость, В - точка касания, А - точка принадлежащая плоскости α, АМ = 1 см, М - точка пересечения АО и сферы (рис. 4).

Решение: (см). В, М - точки, лежащие на сфере, значит, ОМ = OB = R = 4 см. Рассмотрим прямоугольный треугольник ОВА с ∠B = 90° (В - точка касания ОВ = R). (Ответ: 3 см.)

Два взаимно перпендикулярных сечения сферы равноудалены от ее центра. При этом центр сферы находится на расстоянии 4√2 см от общей хорды этих сечений, равной 6 см.

Найдите площадь сферы.

Дано: сфера с центром в точке О, АВ ⊥ CD, АВ - диаметр сечения, CD - диаметр сечения MN – общая хорда. MN = 6 см, ОК = 4√2, ОО1 = ОО2 (рис. 5).

Решение: Рассмотрим прямоугольный ΔONK с ∠OKN = 90°; (Ответ: 164π см2.)

VI. Подведение итогов

Вспомним, по какой формуле вычисляется площадь сферы.

I уровень. П. 60-62, № 593, 595.

(Ответ: 16π дм2, 8π см2, 48π см2.)

(Ответ: см.)

II уровень. № 598, 597, 600.

№ 597. L - радиус круга (Ответ: 10 м.)

№ 598. Дано: сфера с центром в точке О и радиусом R; r1 и r2 - радиусы параллельных сечений сферы, r1 = 9 см, r2 = 12 см, l = 3 см - расстояние между секущими плоскостями (рис. 6).

Решение: Проведем диаметры перпендикулярно к данным параллельным сечениям. Через диаметр проведем секущую плоскость, которая пересечет сферу по окружности, радиус которой равен радиусу сферы ND = r1 = 9 см, MB = r2 = 12 см, NM= 3 см, OD = ОВ = R в ΔOВМ: в ΔODN:

(Ответ: 900π см2.)

Цилиндр получен путем вращения квадрата ABCD вокруг стороны Следовательно,

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

На этом уроке мы поговорим о формуле для вычисления площади поверхности сферы. Узнаем, какой многогранник называется описанным около сферы. А также решим несколько задач на применение формулы для вычисления площади сферы.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Площадь сферы"

Прежде чем приступить к рассмотрению данной темы, давайте вспомним, что такое сфера.

Итак, сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Причём, данная точка называется центром сферы, а данное расстояние – радиусом сферы.

Ранее вы уже познакомились с понятием касательной плоскости к сфере, её свойством, а также с признаком касательной плоскости к сфере.

Вспомним их. Итак, плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

Свойство касательной плоскости к сфере: радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Признак касательной плоскости к сфере: если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Перейдём к рассмотрению вопроса о нахождении площади сферы.

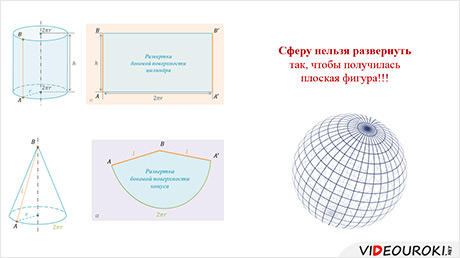
В отличие от боковых поверхностей цилиндра и конуса сферу нельзя развернуть так, чтобы получилась плоская фигура.

Поэтому для сферы не подходит способ определения и вычисления площади поверхности с помощью развертки.

Для определения площади сферы воспользуемся понятием описанного многогранника.

Определение:

Многогранник называется описанным около сферы (шара), если сфера касается всех его граней.

При этом сфера называется вписанной в многогранник.

Говорят, что сфера касается грани многогранника, если плоскость грани является касательной к сфере и точка касания принадлежит грани. Понятно, что центр О сферы с радиусом , вписанной в многогранник, находится на расстоянии, равном радиусу сферы, от каждой из плоскостей, содержащих грани многогранника.

На экране вы видите примеры описанных около сферы многогранников.

Тетраэдр, куб и октаэдр называются описанными около сферы. В свою очередь, сфера называется вписанной в многогранник. Обратите внимание, плоскость каждой грани многогранника является касательной к сфере.

Рассмотрим последовательность описанных около данной сферы многогранников. То есть пусть около сферы описан многогранник, который имеет граней.

Будем неограниченно увеличивать число граней так, чтобы при этом наибольший размер каждой грани многогранника стремился к нулю.

Наибольшим размером грани мы будем называть наибольшее расстояние между двумя точками грани. Например, если грань является прямоугольником, то её наибольший размер равен диагонали. Представим себе, что количество граней многогранника стало бесконечно много. Тогда площадь поверхности многогранника будет приближаться к площади сферы.

За площадь сферы можно принять предел последовательности площадей поверхностей этих многогранников при стремлении к нулю наибольшего размера каждой грани, который равен . Существование этого предела мы докажем при изучении объема шара.

Таким образом, площадь сферы можно вычислить по формуле , где – радиус сферы.

Задача: найдите площадь сферы, радиус которой равен см.

Решение: запишем формулу для вычисления площади сферы.

По условию задачи радиус сферы равен см. Подставим длину радиуса в формулу. Получим, что площадь сферы равна . Запишем ответ.

Задача: площадь сферы равна см 2 . Найдите радиус сферы.

Решение: запишем формулу для вычисления площади сферы.

И выразим из неё радиус. Получили, что радиус сферы можно вычислить по формуле: . Не забудем записать ответ.

Задача: площадь сечения сферы, проходящего через её центр, равна см 2 . Найдите площадь сферы.

Решение: запишем формулу для вычисления площади сферы.

Рассмотрим внимательно рисунок.

Напомним, что сечение сферы плоскостью есть окружность. Так как по условию задачи сечение сферы проходит через её центр, то сечение будет иметь радиус равный радиусу сферы .

Площадь сечения (окружности) вычисляется по формуле . Отсюда, найдём радиус (см).

Подставим найденный радиус в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

Задача: около сферы описан куб с ребром, равным см. Вычислите площадь сферы.

Решение: запишем формулу для вычисления площади сферы.

Напомним, что многогранник называется описанным около сферы, если сфера касается всех его граней.

При этом плоскость каждой грани куба является касательной к сфере. А по свойству касательной плоскости к сфере: радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Значит, диаметр нашей сферы равен длине ребра куба (см). Отсюда, радиус сферы равен (см).

Подставим радиус сферы в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

Не забудем записать ответ.

На этом уроке мы вспомнили формулу для вычисления площади поверхности сферы. Узнали, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Урок изучения нового материала

Планируемые образовательные результаты

1.ознакомиться с формулой площади сферы;

2.научиться решать задачи по данной теме.

1. формировать умение ставить и формулировать для себя новые задачи в учебе и познавательной деятельности.

Развивать трудолюбие, дисциплинированность, уважение к одноклассникам, формировать интерес к геометрии.

сфера, центр, радиус, диаметр сферы

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА

1. ЭТАП Оргмомент .

Цель – активизация учащихся.

Коммуникативные УУД (планирование учебного сотрудничества с учителем и сверстниками)

Личностные УУД (самоопределение )

1. приветствие учителя и учащихся;

2. фиксация отсутствующих;

3. проверка подготовленности учащихся к уроку

4. организация внимания.

2. ЭТАП Актуализация знаний. Фронтальный опрос

Познавательные УУД :

(Анализ объектов с целью выделения признаков)

Личностные УУД: (Формулировать собственное мнение и аргументировать его.)

Коммуникативные : вступать в диалог. Участвовать в коллективном обсуждении учебной проблемы.

Оформлять свои мысли в устной и письменной форме .

3 ЭТАП. Целеполагание и мотивация. Обеспечение мотивации учения детьми, принятия ими целей урока

Регулятивные: Принимают познавательную цель, сохраняют ее при выполнении учебных действий, регулируют весь процесс их выполнения и четко выполняют требования к познавательной задаче.

Какой материал мы изучили на прошлых уроках?

Но при изучении всех фигур на плоскости и тел в пространстве мы обязательно изучали очень важный вопрос относительно одной из величин. О чем идет речь?. Это и будет тема нашего урока. Определите цели и задачи урока.

Записывают в тетради дату

рассмотрели случаи взаимного расположения сферы и плоскости и познакомились с понятием касательной плоскости к сфере.

это площадь сфер

-Повторить и систематизировать знания по уже изученным темам;

- Изучить формулу для вычисления площади сферы;

- Научиться применять ее при решении задач;

- Развивать умение логически мыслить, рассуждать, делать выводы

4 ЭТАП. Изучение нового материала. Опыты.

КоммуникативныеУУД ( Постановка вопросов)

Познавательные УУД (самостоятельное выделение-формулирование познавательной цели)

Проводят наблюдение и эксперимент под руководством учителя, анализируют, сравнивают, обобщают факты и явления.

Познавательные: (эмпирический эксперимент, формулируют выводы наблюдений, сравнивают).

Познавательные: применение полученных знаний в решении практической задачи

На прошлых занятиях вы познакомились с определением касательной плоскости к сфере, её свойством, а также с признаком касательной плоскости к сфере.

Сферу нельзя развернуть на плоскость, в отличие от боковой поверхности цилиндра или конуса, поэтому здесь непригоден способ вычисления и определения площади поверхности с помощью развёртки.

Задача: найдите площадь сферы, радиус которой равен см.

Задача: около сферы описан куб с ребром, равным см. Вычислите площадь сферы.

касательной плоскостью называется плоскость, имеющая со сферой только одну общую точку, данную общую точку называют точкой касания.

радиус сферы перпендикулярен касательной плоскости, если он проведён в точку касания плоскости и сферы.

Решение: запишем формулу для вычисления площади сферы.

Напомним, что многогранник называется описанным около сферы, если сфера касается всех его граней.

Значит, диаметр нашей сферы равен длине ребра куба (см). Отсюда, радиус сферы равен (см).

Подставим радиус сферы в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

5 ЭТАП. Усвоение новых знаний

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Определение

Круг – это часть плоскости, ограниченная окружностью.

Определение

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Уравнение сферы

Определение

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Определение

Сегмент шара - это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Определение

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Определение

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение

Тело, ограниченное сферой, называется шаром.

Сферу можно получить ещё одним способом - вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Определение

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Площадь круга вычисляется по формуле: S_кр=πR 2 .

Площадь поверхности шара вычисляется по формуле: S_сф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Площадь сферы равна S_сф=4πR 2 . То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

Читайте также: