Параллельная проекция и ее свойства конспект кратко

Обновлено: 05.07.2024

При проецировании на плоскость проекций формы и размеры некоторых геометрических элементов могут искажаться. Однако существуют некоторые их свойства, которые всегда остаются неизменными (инвариантными).

1. Проекция точки есть точка.

Это очевидно из самого определения проекции как точки пересечения проецирующего луча с плоскостью проекций.

Следует помнить, что любой точке пространства соответствует только одна проекция на плоскости. Обратная формулировка этого свойства неверна, т.к. каждой проекции точки может соответствовать бесчисленное множество точек в пространстве. Это значит, что одна проекция точки не определяет ее положение в пространстве.

2. Проекцией прямой в общем случае является прямая.

Все проецирующие лучи, проходящие через прямую, заданную отрезком АВ, образуют проецирующую плоскость АВВ¢А¢, которая пересекает плоскость проекций по прямой (рис. 1.3 а). Исходя из этого справедливо и следующее утверждение.

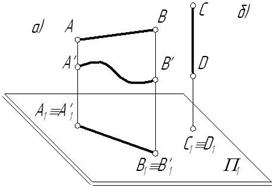
3. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций (рис.1.3а).

4. Проекцией прямой, параллельной направлению проецирования, является точка.

Она называется вырожденной проекцией прямой (рис. 1.3б).

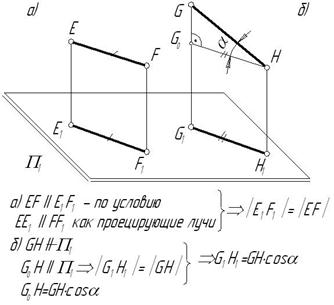
5. а) Если отрезок параллелен плоскости проекций, то он проецируется на нее в натуральную величину.

б) В противном случае, при прямоугольном параллельном проецировании он имеет проекцию меньшую истиной величины.

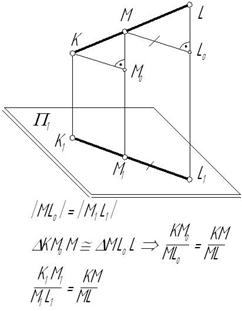
6. Если точка принадлежит прямой, то проекция этой точки лежит на проекции этой прямой.

7. Если точка, лежащая на прямой, делит ее на отрезки в каком-либо отношении, то проекция этой точки поделит проекцию этой прямой в том же отношении.

8. Если прямые пересекаются, то их проекции тоже пересекаются. Причем проекция точки пересечения прямых является точкой пересечения проекций.

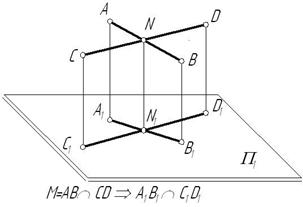
Точка N одновременно принадлежит прямым (A-B) и (C-D). По шестому инвариантному свойству проекция этой точки должна принадлежать проекциям этих прямых, а следовательно, быть точкой пересечения проекций.

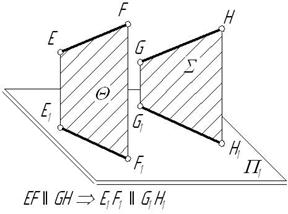
9. Проекции параллельных прямых параллельны между собой.

Плоскости Q и S, проходящие через две параллельные прямые, параллельны, т.к. две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости.

Параллельные плоскости пересекаются с третьей плоскостью по параллельным прямым, следовательно, .

1. Проекция точки есть точка.

2. Проекцией прямой в общем случае является прямая.

4. Проекцией прямой, параллельной направлению проецирования, является точка.

Она называется вырожденной проекцией прямой (рис. 1.3б).

5. а) Если отрезок параллелен плоскости проекций, то он проецируется на нее в натуральную величину.

6. Если точка принадлежит прямой, то проекция этой точки лежит на проекции этой прямой.

9. Проекции параллельных прямых параллельны между собой.

Параллельные плоскости пересекаются с третьей плоскостью по параллельным прямым, следовательно, .

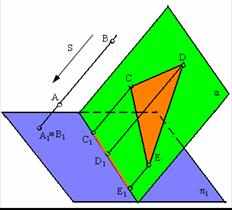
Геометрические фигуры проецируются на плоскость проекции, в общем случае, с искажениями. Причем характер искажений проекций по сравнению с оригиналом зависит от аппарата проецирования и положения проецируемой фигуры по отношению к плоскости проекции. В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Действительно, пусть дана прямоугольная трапеция ABCD. Плоскость трапеции не параллельна плоскости проекции α. Определим параллельную проекцию при заданном направлении проецирования s.

Из рисунка видно, что проекция ABCD Существенно отличается от оригинала ABCD. Изменились длины сторон трапеции, другими стали величины углов при ее вершинах. При таких условиях, естественно, нарушается равенство площадей фигуры оригинала и ее проекции.

Наряду с этим, между оригиналом и его проекцией существует определенная связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Такие свойства принято называть проективными или инвариантными (независимыми) для данного способа проецирования.

Основу любой геометрии составляет система аксиом. Любые геометрические определения и предложения, равно как и доказательства теорем, базируются на принятой системе аксиом. В процессе параллельного проецирования (получения проекций геометрической фигуры по ее оригиналу) или реконструкции чертежа (воспроизведение оригинала по заданным его проекциям), любое определение, любую теорему можно составить и доказать, опираясь на инвариантные свойства параллельного проецирования, которые играют в начертательной геометрии такую же важную роль, как аксиомы в геометрии.

Таким образом, можно утверждать, что в начертательной геометрии существует, как бы, две системы аксиом: - первая используется в процессе построения проекции геометрической фигуры по ее оригиналу. На этом этапе функции аксиом выполняют инвариантные свойства параллельного проецирования; После того, как проекции определены, можно рассматривать задачу как плоскую, вступает в силу вторая система - аксиоматика евклидовой геометрии.

Основные инвариантные свойства параллельного проецирования:

1. Проекция точки есть точка.

2. Проекция прямой на плоскость есть прямая.

Действительно, при параллельном проецировании все лучи, проецирующие точки A,B,C,D,E прямой l, принадлежат одной плоскости Υ, параллельной направлению проецирования s. Эта плоскость пересекает плоскость проекции по прямой l α . (Исходя из этого справедливо и следующее утверждение. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций.)

3. Если в пространстве точка принадлежит (инцидентна) линии, то проекция этой точки принадлежит проекции линии. Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.

4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.

Если [AB]║[CD], то плоскости ABB α A α и CDD α C α параллельны как имеющие углы при вершинах B и D с соответственно параллельными сторонами - (BA)║(DC) и (BB α )║(DD α ). Эти плоскости пересекаются плоскостью проекции α по параллельным прямым l α ₁║l α ₂. Проведем в проецирующей плоскости ABB α A α через точку A прямую k₁║l₁, а в плоскости CDD α C α прямую k₂║l₂. Эти прямые пересекут проецирующие лучи [BB α ) и [DD α ) в точках E и F. Отрезок [AE] [A α B α ], а [CF] [C α F α ] как отрезки параллельных между параллельными. ΔABE подобен ΔCDF. На основании подобия треугольников можно записать:

Из четвертого свойства следует:

а) если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией этой точки в том же отношении.

Доказательство этого свойства аналогично предыдущему, понятно из чертежа на рисунке и не требует дополнительных пояснений.

Как следствие пункт a) можно записать: середина отрезка оригинала проецируется в середину его проекции. Поэтому медианы треугольника проецируются в медианы его проекций, а следовательно, центр тяжести треугольной пластинки проецируется в центр тяжести треугольника - проекций; центр окружности, как точка, делящая все диаметры пополам, проецируется в центр эллипса. Взаимно перпендикулярные диаметры окружности проецируются в сопряженные диаметры эллипса.

б) Проекции конгруентных отрезков взаимно параллельных прямых взаимно параллельны и конгруэнтны.

Поэтому проекцией любого параллелограмма будет параллелограмм. В параллелограммы проецируется также произвольно расположенный по отношению к плоскости проекции прямоугольник, ромб, квадрат.

5. Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых. Пусть две прямые a и b пересекаются в точке K. Так как точка K принадлежит прямой a, то на основании свойства 3 K α ∈ a α . Одновременно K ∈ b, следовательно, K α ∈ b α . Эти два условия могут быть удовлетворены только в том случае, если K α будет точкой пересечения проекций прямых a и b.

6. Плоская фигура, параллельная плоскости проекции, проецируется на эту плоскость в конгруентную фигуру.

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.

Следствием этого свойства будут: - плоская ломанная линия проецируется, в общем случае, в ломанную линию с тем же числом вершин; - плоская кривая проецируется, в общем случае, в кривую линию; - проекция в виде отрезка прямой не определяет оригинала, которым могут быть: прямая, плоская ломанная или кривая линии, любая плоская фигура.

8. Параллельный перенос оригинала или плоскости проекции не изменяет вида и размеров проекции оригинала.

Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций.

Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования.

Рассмотрим основные инвариантные свойства параллельного проецирования.

1. Проекция точки есть точка

Это очевидно из самого определения проекции как точка пересечения проецирующей прямой с плоскостью.

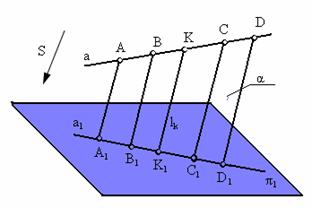
2. Проекция прямой есть прямая (рис. 1.6)

Рис. 1.6. Инвариантные свойства 2, 3, 4

Все проецирующие прямые, проходящие через точки прямой а параллельно направлению проецирования S, образуют проецирующую, или лучевую, плоскость α.

Проекция прямой а на плоскость π₁ определяется как линия пересечения этой лучевой плоскостиαс плоскостью π₁, т. е. прямая

Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой (рис. 1.6).

Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.

Если точка К принадлежит прямой а и плоскости α, то и проецирующий луч l_К принадлежит плоскости α. Следовательно, этот луч пересечет плоскость π₁ в линии пересечения плоскостей α и π₁, т. е. в точке К₁, принадлежащей проекции прямой а₁.

4. Если точка К делит отрезок АD в отношении m : n то и проекция этой точки делит в таком же отношении проекцию этого отрезка (рис. 1.6):

Фигура ADD₁A₁ – трапеция. Прямая КК₁ параллельна основаниям трапеции АА₁ и DD₁, следовательно делит ее стороны АD и А₁D₁ на пропорциональные части.

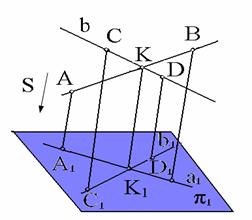
5. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых (рис. 1.7)

Рис. 1.7. Пример инвариантного свойства 5

Действительно, точка К принадлежит одновременно прямым АВ и CD. По третьему инвариантному свойству проекция этой точки К₁ должна принадлежать проекциям этих прямых, т. е. должна являться точкой пересечения этих проекций.

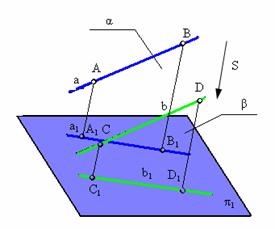
6. Проекции параллельных прямых параллельны (рис. 1.8)

Лучевые плоскости α и β, проходят через параллельные прямые АВ и CD. Они параллельны, так как две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (АВ CD и АА₁ СС₁). Но две параллельные плоскости пересекаются с третьей по параллельным прямым, следовательно, А₁В₁ С₁D₁.

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.

Исключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 1. 9).

Рис. 1.8. Пример инвариантного свойства

Рис. 1.9. Примеры инвариантных свойств 7, 8

8. Прямая, параллельная направлению проецирования, проецируется в точку (рис. 1.9)

9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре (рис. 1.10).

Следствия этого инвариантного свойства следующие:

1. Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку (рис. 1.10):

2. Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу (рис. 1.10).

В этом видеоуроке мы напомним, что называют параллельным проектированием. Вспомним основные его свойства. Повторим, как свойства параллельного проектирования применяются при выполнении рисунков, иллюстрирующих теоремы и задачи стереометрии.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Параллельное проектирование. Изображение пространственных фигур"

В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры.

Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.

Пусть — некоторая плоскость, а — некоторая прямая, пересекающая эту плоскость. Возьмём в пространстве произвольную точку . Если точка не лежит на прямой , то проведём через точку прямую, параллельную прямой , и обозначим через точку пересечения этой прямой с плоскостью . Если же точка лежит на прямой , то обозначим через точку пересечения прямой с плоскостью .

Точка называется проекцией точки на плоскость при проектировании параллельно прямой (или параллельной проекцией точки ).

Плоскость называется плоскостью проекций, а о прямой говорят, что она задаёт направление проектирования.

Все прямые, параллельные прямой , задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми.

Пусть — плоская или пространственная фигура. Проекцией фигуры на плоскость при проектировании параллельно прямой называется множество проекций всех точек фигуры.

Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.

Вспомним основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.

1. Проекция прямой есть прямая, а проекция отрезка — отрезок.

2. Проекции параллельных прямых параллельны или совпадают.

3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.

Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции.

При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых.

Если точка делит отрезок в отношении , то проекция точки будет делить проекцию отрезка также в отношении .

Центр правильного треугольника отображается в точку пересечения медиан проекции этого треугольника, центр квадрата — в точку пересечения диагоналей проекции квадрата.

А теперь давайте поговорим об изображении пространственных фигур.

Рассмотренные свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.

Изображением фигуры называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.

Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.

При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.

Например, вы видите фигуры, которые являются изображениями куба.

Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.

При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.

Итак, проекцией треугольника может быть любой треугольник.

При этом величины углов и отношение длин непараллельных сторон не сохраняются, но при этом медианы треугольника отображаются в медианы его проекции. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.

Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность.

В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.

Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований.

Правильный шестиугольник проектируется в искажённый шестиугольник с сохранением параллельности противолежащих сторон.

Окружность проектируется в эллипс, большая ось которого имеет длину, равную диаметру окружности.

При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно считать изображением треугольной пирамиды при определённом выборе направления проектирования и плоскости, на которую проектируется эта пирамида.

Например, фигуры, изображённые на экране, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.

Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.

При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.

Аналогичным образом изображается прямоугольный параллелепипед.

Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.

Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.

Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.

Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. Точки и находятся по одну сторону от плоскости . Точки и — их параллельные проекции на эту плоскость, причём . Постройте точку пересечения прямой с плоскостью . И найдите расстояние между серединой отрезка и её проекцией на плоскость , если и см.

Задача вторая. На диагонали параллелепипеда взята точка , а на прямой – точка так, что отрезки и параллельны. Найти их отношение.

Читайте также: