Нормальный закон распределения конспект

Обновлено: 05.07.2024

Непрерывная случайная величина , распределённая по нормальному закону, имеет функцию плотности (не пугаемся) и однозначно определяется параметрами и .

Эта функция получила фамилию некоронованного короля математики, К.Ф. Гаусса и в своё время была изображена вместе с его портретом на купюре в 10 немецких марок. Для функции Гаусса выполнены общие свойства плотности, а именно (почему?) и , откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.

Следующие замечательные факты я тоже приведу без доказательства:

Задача 118
Нормально распределённая случайная величина задана параметрами . Записать её функцию плотности и построить график.

Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей.

Решение начнём шаблонной фразой: функция плотности нормально распределённой случайной величины имеет вид . В данном случае и:

Сначала полная картина, затем комментарии:

На первом шаге декартову систему координат. При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:

по оси абсцисс: 2 тетрадные клетки = 1 ед.,
по оси ординат: 2 тетрадные клетки = 0,1 ед., при этом саму ось следует расположить из тех соображений, что в точке функция достигает максимума, и вертикальная прямая (на чертеже её нет) является линией симметрии графика.

И логично, что в первую очередь удобно найти максимум функции:

Отмечаем вершину графика (красная точка).
Далее вычислим значения функции при , а точнее только одно из них – в силу симметрии графика они равны:

Отмечаем синим цветом.

Внимание! и – это точки перегиба нормальной кривой. На интервале график является выпуклым вверх, а на крайних интервалах – вогнутым вниз.

Далее отклоняемся от центра влево и право ещё на одно стандартное отклонение и рассчитываем высоту:

Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно.

Поговорим о том, как меняется форма нормальной кривой в зависимости от значений и .

Зачем это нужно? Дело в том, что значения скрупулезно подсчитаны нашими предками и сведены в специальную таблицу, которая есть во многих книгах по терверу. Но ещё чаще встречается таблица значений функции Лапласа:
, и с этой функцией и этой таблицей (см. Приложение Таблицы) мы уже имели дело в интегральной теореме Лапласа.

Итак, вероятность того, что нормальная случайная величина с параметрами и примет значение из интервала , можно вычислить по формуле:
, где – функция Лапласа.

И ещё в этом заключена большая мудрость – если вдруг пропадёт электричество или восстанут машины, то у человечества останется возможность заглянуть в бумажные таблицы и спасти мир =) Классика жанра:

Задача 119
Из пункта ведётся стрельба из орудия вдоль прямой . Предполагается, что дальность полёта распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадёт с перелётом от 5 до 70м.

Решение: в задаче рассматривается нормально распределённая случайная величина – дальность полёта снаряда, и по условию .

Так как речь идёт о перелёте за цель, то . Вычислим вероятность – того, что снаряд упадёт в пределах этой дистанции.

Если в вашей методичке дана таблица значений функции , то используйте формулу :

Но гораздо чаще, и в этом курсе в частности, встречается таблица значений функции Лапласа , поэтому решаем через неё:

Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета.

Напоминаю, что . Всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.

Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием:

– с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов

Задача 120
Диаметр подшипников, изготовленные на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.

В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что согласно формулировке, в этой задаче корректнее будет включить концы интервала в рассмотрение.

И уже в этом примере нам встретился особый случай – когда интервал симметричен относительно математического ожидания. В такой ситуации его можно записать в виде и, пользуясь нечётностью функции Лапласа , упростить рабочую формулу :

– вероятность того, что значение случайной величины отклонится от математического ожидания менее чем на .

Таким, образом задача про подшипники решается гораздо короче:
– вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.

Задача 121
Случайная величина ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.

– вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.

Ответ:

…срочно разрабатываю курс по подготовке продавцов =)

Самостоятельно решаем обратную задачу:

Задача 122
Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью попадет длина диаметра валика.

Пункт 5* Калькулятора в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.

И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:

Задача 123
Нормально распределенная случайная величина задана своими параметрами (математическое ожидание) и (среднее квадратическим отклонение). Требуется:

Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании таблицы ;) После чего мы разберём заключительный пример:

Задача 124
Плотность распределения вероятностей случайной величины имеет вид . Найти , математическое ожидание , дисперсию , функцию распределения , построить графики плотности и функции распределения, найти .

функция определена при любом действительном значении , и если её удастся привести к виду , то случайная величина распределена по нормальному закону.

Пробуем привести. Для этого выделяем полный квадрат и организуем трёхэтажную дробь:

Обязательно выполняем проверку, возвращая показатель в исходный вид:

, что мы и хотели увидеть.

Теперь найдём значение параметра . Поскольку множитель нормального распределения имеет вид и , то:
, откуда выражаем и подставляем в нашу функцию:
, после чего ещё раз пробежим глазами и убедимся, что полученная функция имеет вид .

Построим график плотности:

и график функции распределения :

Пару слов на счёт ручного построения последнего графика – на случай отсутствия под рукой Экселя или даже обычного калькулятора. В точке функция распределения принимает значение и здесь находится перегиб графика (малиновая точка).
Кроме того, для более или менее приличного чертежа желательно найти ещё хотя бы пару точек. Берём традиционное значение и стандартизируем его по формуле . Далее по таблице значений функции Лапласа находим: – жёлтая точка на чертеже. С симметричной оранжевой точкой никаких проблем: и:
.

После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.

Да, и ещё нужно вычислить:

– вероятность того, что случайная величина примет значение из данного отрезка.

Задача была непростой, и посему блеснём академичным стилем, ответ:

А теперь обещанный секрет:

понятие о центральной предельной теореме.

которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина является суммой очень большого числа взаимно независимых случайных величин , влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение встречается буквально на каждом шагу.

Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю совокупность. Поэтому скорость молекул воздуха распределена нормально.

Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей популяции, следовательно, продолжительность жизни этих особей тоже распределена по нормальному закону.

Именно этот факт мы и использовали в теоремах Лапласа – когда приближали биномиальные вероятности соответствующими значениями функций нормального распределения.

Подчёркиваю, что теорема Ляпунова носит статус теоремы, а значит, строго доказана в теории.

Но, с другой стороны, гораздо более важнА системная и упорная деятельность, после которой следуют закономерные результаты. Желательно, полезные, конечно J

Гмурман В. Е. Теория вероятностей и математическая статистика (уч. пособие);

Гмурман В. Е. Руководство к решению задач по теории вероятности (задачник с примерами решений).

Везения в главном!

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.

Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей.

В таблице m - число заказов, полученных компанией на покупку телевизора. С_n m - число сочетаний m телевизоров по n, p - вероятность наступления события А, т.е. заказа телевизора, q - вероятность не наступления события А, т.е. не заказа телевизора, P m,n - вероятность заказа m телевизоров из n. На рисунке 1 изображен полигон распределения вероятностей.

2.Геометрическое распределение.

Геометрическое распределение случайной величины имеет следующий вид:

P m - вероятность наступления события А в испытание под номером m.
р - вероятность наступления события А в одном испытании.
q = 1 - p

Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.

Из таблицы видно, что с увеличением числа m, вероятность того, что будет обнаружен бракованный блок, снижается. Последняя строчка (m=10) объединяет две вероятности: 1 - что десятый блок оказался неисправным - 0,038742049 , 2 - что все проверяемые блоки оказались исправными - 0,34867844. Так как вероятность того, что блок окажется неисправным относительно низкая (р=0,1), то вероятность последнего события P m (10 проверенных блоков) относительно высокая. Рис.2.

3.Гипергеометрическое распределение.

Гипергеометрическое распределение случайной величины имеет следующий вид:

Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M - всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m - число правильно угаданных чисел среди изъятых.

Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.

4.Закон распределения Пуассона.

Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:

λ = np = const
n - число испытаний, стремящиеся к бесконечности
p - вероятность наступления события, стремящаяся к нулю
m - число появлений события А

Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B - 0,06 и C - 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.

Из условия имеем: m=100, λ 1 =8, λ 2 =6, λ 3 =4 ( ≤10 )

(таблица дана не полностью)

Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4)

Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.

5.Равномерный закон распределения.

Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин - подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин - индивидуально (базовый уровень). 2000 руб / 120 мин - студенты.

6.Нормальный закон распределения (закон Гаусса).

Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:

где
а - математическое ожидание случайной величины
σ - среднее квадратическое отклонение

График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный:

При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.

Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:

Т.е. вероятность случайной величины Х состоит из двух частей: вероятности где x принимает значения от минус бесконечности до а, равная 0,5 и вторая часть - от а до х. (Рис.7)

7.Показательный закон распределения.

Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид:

где λ - параметр обратно-пропорциональный математическому ожиданию.

График плотности вероятности с параметрами
λ = 2, λ = 4, λ =6 изображен на рис.8

Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид:

График функции изображен на рис.9

Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:

8.Логарифмически-нормальное распределение.

Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид.

Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)

9. χ ² распределение

Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением.

χ ² распределение имеет вид:

А i - i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3. k).

Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:

Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.

10.Распределение Стьюдента (t - распределение)

Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид:

Z - случайная величина, распределенная по нормальному закону.
χ ² - случайная величина, имеющая χ ² - распределение с k степенями свободы.

Плотность вероятности распределения Стьюдента имеет вид:

На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.

11. Распределение Фишера-Снедекора.

Распределение случайной величины Фишера-Снедекора имеет вид:

Плотность вероятности случайной величины имеет вид:

При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)

Без преувеличения его можно назвать философским законом. Наблюдая за различными объектами и процессами окружающего мира, мы часто сталкиваемся с тем, что чего-то бывает мало, и что бывает норма:

Перед вами принципиальный вид функции плотности нормального распределения вероятностей, и я приветствую вас на этом интереснейшем уроке.

Данная функция получила фамилию некоронованного короля математики, и я не могу удержаться, чтобы не запостить:

Одну из таких купюр мне довелось лично держать в руках, и ещё будучи школьником я внимательно изучил функцию Гаусса. Педантичные немцы отобразили все её особенности (на картинке видно плохо), и мы с толком, с расстановкой приступаем к их ~~немцев~~ изучению.

Начнём с того, что для функции выполнены свойства плотности вероятностей , а именно (почему?) и , откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.

Любопытно отметить, что сам по себе неопределённый интеграл является неберущимся, однако указанный выше несобственный интеграл сходится и равен . Вычисления для простейшего случая можно найти здесь, все же остальные варианты сводятся к нему с помощью линейной замены .

Следующие замечательные факты я тоже приведу без доказательства:

Эти значения выводятся с помощью общих формул математического ожидания и дисперсии, и желающие / нуждающиеся могут ознакомиться с подробными выкладками в учебной литературе, и совсем здОрово, если вам удастся провести их самостоятельно.

Нормально распределённая случайная величина задана параметрами . Записать её функцию плотности и построить график.

Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей.

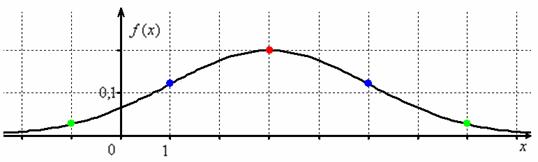
Сначала полная картина, затем комментарии:

Строим декартову систему координат. При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:

по оси абсцисс: 2 тетрадные клетки = 1 ед.;

по оси ординат: 2 тетрадные клетки = 0,1 ед., при этом саму ось следует расположить из тех соображений, что в точке функция достигает максимума, и вертикальная прямая (на чертеже отсутствует) является линией симметрии графика.

И логично, что в первую очередь удобно найти максимум функции. В данном примере он находится в точке :

Отмечаем вершину графика (красная точка).

Далее вычислим значения функции при , а точнее только одно из них – в силу симметрии графика они равны:

Отмечаем синим цветом.

Внимание! – это точки перегиба нормальной кривой. На интервале график является выпуклым, а на крайних интервалах – вогнутым.

Далее отклоняемся от центра ещё на одно стандартное отклонение и рассчитываем высоту:

Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно.

При электронном оформлении решения график легко построить в Экселе, и неожиданно для самого себя я даже записал короткий видеоролик на эту тему. Но сначала поговорим о том, как меняется форма нормальной кривой в зависимости от значений и .

Ну а теперь смотрим кино:

Почти все значения не поддаются точному расчету, но как мы только что видели, с современными вычислительными мощностями с этим нет никаких трудностей. Так, для функции стандартного распределения соответствующая экселевская функция вообще содержит один аргумент:

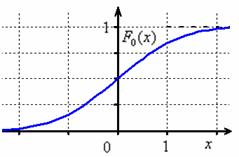
Раз, два – и готово:

На чертеже хорошо видно выполнение всех свойств функции распределения, и из технических нюансов здесь следует обратить внимание на горизонтальные асимптоты и точку перегиба .

! Вспоминаем также, что

Примечание: функцию легко получить из общего случая с помощью линейной замены . Тогда и:

и из проведённой замены как раз следует формула перехода от значений произвольного распределения – к соответствующим значениям стандартного распределения.

Зачем это нужно? Дело в том, что значения скрупулезно подсчитаны нашими предками и сведены в специальную таблицу, которая есть во многих книгах по терверу. Но ещё чаще встречается таблица значений , с которой мы уже имели дело в интегральной теореме Лапласа:

, где – функция Лапласа.

Из пункта ведётся стрельба из орудия вдоль прямой . Предполагается, что дальность полёта распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадёт с перелётом от 5 до 70м.

Если в нашем распоряжении есть таблица значений функции , то используем формулу :

Если же в нашем распоряжении есть таблица значений функции Лапласа , то решаем через неё:

Напоминаю, что , и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.

– с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов

Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.

В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что согласно формулировке, здесь можно включить концы интервала в рассмотрение. Впрочем, это не критично.

И уже в этом примере нам встретился особый случай – когда интервал симметричен относительно математического ожидания. В такой ситуации его можно записать в виде и, пользуясь нечётностью функции Лапласа, упростить рабочую формулу:

– вероятность того, что значение случайной величины отклонится от математического ожидания менее чем на .

Хорошо то решение, которое умещается в одну строчку:)
– вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.

Результат этой задачи получился близким к единице, но хотелось бы ещё бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счёт? Существует! На поставленный вопрос отвечает так называемое

Его суть состоит в том, что практически достоверным является тот факт, что нормально распределённая случайная величина примет значение из промежутка .

И в самом деле, вероятность отклонения от матожидания менее чем на составляет:
или 99,73%

Продолжаем решать суровые советские задачи:

Случайная величина ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.

Решение очень простое. По условию, и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение и по формуле :

– вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.

Ответ:

…срочно разрабатываю курс по подготовке продавцов =)

Самостоятельно решаем обратную задачу:

Диаметр валика – случайная нормально распределенная случайная величина, среднее квадратическое отклонение ее равно мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью попадет длина диаметра валика.

Пункт 5* расчётного макета в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.

И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:

Нормально распределенная случайная величина задана своими параметрами (математическое ожидание) и (среднее квадратическое отклонение). Требуется:

Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании бумажных таблиц ;)

Ну а я разберу пример повышенной сложности:

Плотность распределения вероятностей случайной величины имеет вид . Найти , математическое ожидание , дисперсию , функцию распределения , построить графики плотности и функции распределения, найти .

Так как функция определена при любом действительном значении , и её можно привести к виду , то случайная величина распределена по нормальному закону.

Приводим. Для этого выделяем полный квадрат и организуем трёхэтажную дробь:

Обязательно выполняем проверку, возвращая показатель в исходный вид:

, что мы и хотели увидеть.

Теперь найдём значение параметра . Поскольку множитель нормального распределения имеет вид и , то:
, откуда выражаем и подставляем в нашу функцию:
, после чего ещё раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид .

Построим график плотности:

и график функции распределения :

Если под рукой нет Экселя и даже обычного калькулятора, то последний график легко строится вручную! В точке функция распределения принимает значение и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти ещё хотя бы пару точек. Берём традиционное значение и стандартизируем его по формуле . Далее с помощью таблицы значений функции Лапласа находим: – жёлтая точка на чертеже. С симметричной оранжевой точкой никаких проблем: и:
.

После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.

Да, и ещё нужно вычислить:
– вероятность того, что случайная величина примет значение из данного отрезка.

Ответ:

Но этим, конечно, всё дело не ограничивается! Дополнительные примеры, причём довольно творческие, можно найти в тематической pdf-книжке.

И в заключение урока обещанный секрет:

понятие о центральной предельной теореме

которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина является суммой очень большого числа взаимно независимых случайных величин , влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение (близкое к нему) и встречается буквально на каждом шагу.

Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей популяции, следовательно, длина их лапок тоже распределена по нормальному закону.

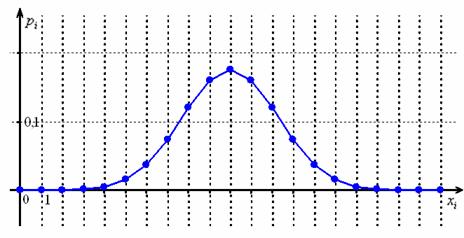
Уже при и в многоугольнике биномиального распределения хорошо просматривается нормальная кривая:

И чем больше , тем ближе будет сходство. Вероятность может быть и другой, но не слишком малой.

Вот такие вот пироги.

До скорых встреч!

Решения и ответы:

Пример 3. Решение: т.к. случайная величина (диаметр подшипника) распределена нормально, то используем формулу , где – функция Лапласа. В данном случае:

– вероятность того, что диаметр наугад взятого подшипника будет находиться в пределах от 1,4 до 1,6 см.

Пример 5. Решение: используем формулу: .
В данной задаче , таким образом:

откуда находим:

Длина искомого интервала составляет

Ответ: 20 мм

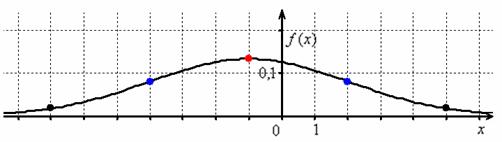
Пример 6. Решение: функция плотности нормально распределённой случайной величины имеет вид , где – математическое ожидание, – стандартное отклонение. В данном случае , следовательно:

Выполним чертёж:

! Примечание: несмотря на то, что условие допускает схематическое построение графика, на чертеже обязательно отображаем все его принципиальные особенности, в частности, на забываем о перегибах в точках .

б) Используем формулу , где – функция Лапласа.
В данной задаче :

– вероятность того, что случайная величина примет значение из данного интервала.

в) Используем формулу для :
– вероятность того, что значение случайной величины отклонится от её математического ожидания не более чем на 2.

Ответ: а) , б) , в) , г)

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Лекция 18. Нормальное распределение. Применение данного понятия при исследовании.

Одним из важнейших в математической статистике является понятие нормального распределения.

Нормальное распределение (называемое также распределением Гаусса), характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине – часто.

Нормальное распределение возникает, когда данная случайная величина представляет собой сумму большого числа независимых случайных величин, каждая из которых играет в образовании всей суммы незначительную роль.

Разность наибольшего и наименьшего значений случайной величины выборки называется её размахом и обозначается R.

Пример: Задана выборка 80,80,330,4500.

Отклонением от среднего называют разность между рассматриваемым значением случайной величины и средним значением выборки.

Пример: Задана выборка 52,54,50,48,46.

Пусть значение величины X1=52, а значение среднего X̅= (52+54+50+48+46): 5 =50, отклонение от среднего X1−X̅=52−50=2.

Очевидно, отклонение от среднего может быть как положительным, так и отрицательным числом.

Нетрудно понять, что сумма отклонений всех значений выборки от среднего значения равна нулю. Поэтому характеристикой стабильности элементов совокупности может служить сумма квадратов отклонений от среднего (чем меньше, тем лучше).

Среднее арифметическое квадратов отклонений называется дисперсией и обозначается D.

Для оценки степени отклонения от среднего значения удобно иметь дело с величиной той же размерности, что и сама величина X.

С этой целью используют значения корня квадратного из дисперсии σ=√D. Корень квадратный из дисперсии называют средним квадратичным отклонением и обозначают σ=√Dσ.

Задания для самостоятельной работы по теме:

1.Найти размах выборки: 15, -7, 13, -6, 8, 2, 1, -8, -2;

2.Найти дисперсию выборки: 1) 10 см, 12 см, 7 см, 11 см;

3.Найти среднее квадратичное отклонение от среднего значения элементов выборки: 3 кг, 5 кг, 5кг, 8 кг, 4 кг;

Читайте также: