Непрерывность функции имеющей производную дифференциал 11 класс никольский конспект
Обновлено: 06.07.2024
Презентация на тему: " 1 2 Определение производной функции в точке Непрерывность дифференцируемой функции Дифференциал функции Геометрический смысл производной и дифференциала." — Транскрипт:
2 2 Определение производной функции в точке Непрерывность дифференцируемой функции Дифференциал функции Геометрический смысл производной и дифференциала Физические приложения производной и дифференциала
3 3 Определение производной функции в точке Пусть функция f(x) определена в некоторой окрестности точки x 0. ОПРЕДЕЛЕНИЕ. Если существует (конечный) предел отношения то f(x) называется дифференцируемой точке х 0, а сам предел называется производной функции f(x) в точке х 0 и обозначается f '(x 0 ), то есть Обозначим x = x – x 0 – приращение аргумента при переходе из точки х 0 в точку х, а y = f(x 0 + x) – f(x 0 ) – соответствующее приращение функции. Тогда производная функции f(x) в точке х 0 предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю.
4 4 Пример 1. Приведем примеры вычисления производных некоторых простейших элементарных функций, исходя из определения производной. y = a x (0 0.Считая, что | х | 0 – произвольная точка, то
5 5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R.
6 6 ТЕОРЕМА. Если функция f(x) дифференцируема в точке x 0, то она непрерывна в этой точке. Доказательство. Пусть существует Тогда Отсюда получим, что f (x) – f (x 0 ) = f '(x 0 ) (х – х 0 ) + (х – х 0 )α(x) при х х 0. То есть f(x) непрерывна в точке x 0. Непрерывность дифференцируемой функции (1)
7 7 ЗАМЕЧАНИЕ. Непрерывность функции в точке не является достаточным условием существования в этой точке производной. Пример 5. f (x) = х. Исследуем поведение f (x) в окрестности х 0 = 0. Здесь и f (x) f (0) = 0 при x 0. Т.е. функция непрерывна в точке х 0 = 0. Рассмотрим x y 0 Предел не существует, так как Итак, функция f (x) = х не имеет производной в точке х = 0, хотя непрерывна в этой точке
8 8 Пример x y 0 при х 0. при х 0. Т.е. f(x) непрерывна в точке х = 0. Т.е. f(x) не имеет производной в точке х = 0 и, следовательно, не дифференцируема в этой точке. Исследуем поведение f (x) в окрестности точки х = 0.
9 9 Пусть функция у = f(x) дифференцируема в точке х 0. Тогда, согласно (1), ее приращение в точке х 0 можно записать в виде y = f(x 0 + x) – f(x 0 ) = f (x 0 ) х + о( x) при х. Дифференциал функции f (x 0 ) x – главная линейная относительно x часть приращения функции у = f(x) в точке х 0 называется дифференциалом функции в точке х 0 при приращении x и обозначается df(х 0 ; x) или df(х 0 ) или df или dу. y = f(x 0 + x) – f(x 0 ) = df(х 0 ; x) + о( x) при х. ОПРЕДЕЛЕНИЕ. Главная часть приращения, линейная относительно х. Бесконечно малая более высокого порядка, чем х. Теперь приращение функции можно записать так:
10 10 ЗАМЕЧАНИЕ. Приращение х часто обозначают символом dх и называют дифференциалом независимой переменной. Таким образом, дифференциал функции в точке x 0 можно записать в виде df(х 0 ) = f '(x 0 ) dх. Если функция дифференцируема в каждой точке некоторого интервала, то ее дифференциал dy – функция от х и dx: dy = f '(x) dx. Отсюда, в частности, получается выражение для производной То есть производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
11 11 Геометрический смысл производной и дифференциала Пусть функция у = f(x) определена в U(x 0 ) и дифференцируема в точке х 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + у 0 L – секущая L 0 – касательная x y = f(x 0 + x) – f(x 0 ) при х в силу непрерывности функции. Касательной к графику функции у = f(x) в точке М 0 называется предельное положение секущей L при х. y Если функция дифференцируема в точке х 0, то в уравнении секущей у/ х f (x 0 ) при х и уравнение касательной имеет вид у = у 0 + f (x 0 ) (х – х 0 ).
12 12 М0М0 М x0x0 x 0 + x dy = df(х 0 ; x) = f (x 0 ) x x y = f(x) f(x0)f(x0) f(x 0 + x ) 0 x y F E EM = o( x ) при x 0 L0L0 tg = f (x 0 ) Если же у/ х при х, то прямая х = х 0, получающаяся из уравнения секущей, называется вертикальной касательной к графику функции в точке М 0. Из уравнения касательной получим у – у 0 = f (x 0 ) (х – х 0 ) = df(х 0 ) – приращение ординаты касательной при переходе из точки х 0 в точку х. Нормалью к графику функции в точке М 0 называется прямая, перпендикулярная касательной, проходящая через точку М 0. Ее уравнение имеет вид у = у 0 – 1/f (x 0 ) (х – х 0 ). L 1 – нормаль
13 13 Физические приложения производной и дифференциала Если S(t) – путь, пройденный материальной точкой за время t, то S '(t) – мгновенная скорость материальной точки, а dS = S '(t)dt – расстояние, которое прошла бы материальная точка за промежуток времени от t до t + dt, если бы она двигалась со скоростью, равной мгновенной скорости в момент t. Если Q(t) – количество электричества, протекающего через поперечное сечение проводника в момент времени t, то Q '(t) = I – сила тока. Если N(t) – количество вещества, образующегося в момент t в ходе химической реакции, то N '(t) – скорость химической реакции.
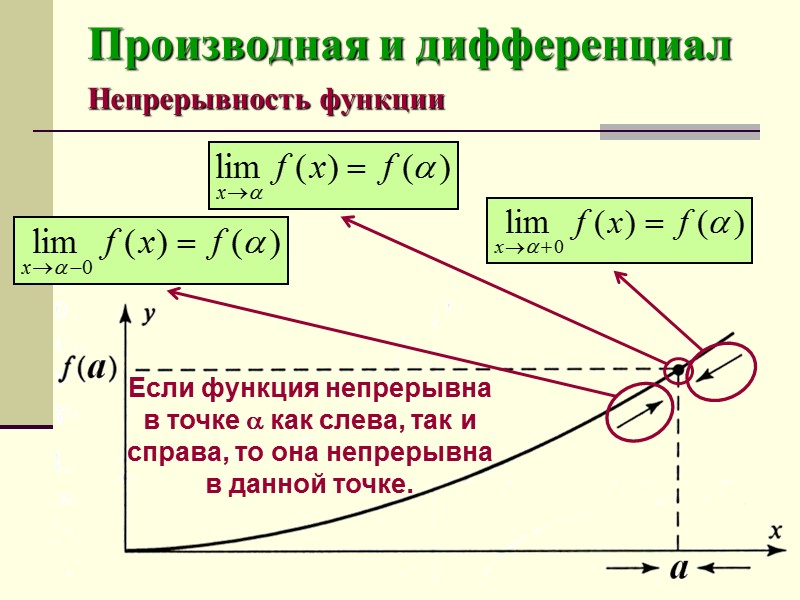

Производная и дифференциал Непрерывность функции Если функция непрерывна в точке как слева, так и справа, то она непрерывна в данной точке.
Производная и дифференциал Точки разрыва Точки, в которых функция не является непрерывной, называются точками разрыва. Разрывы I рода Разрывы II рода Устранимые Неустранимые Неустранимые
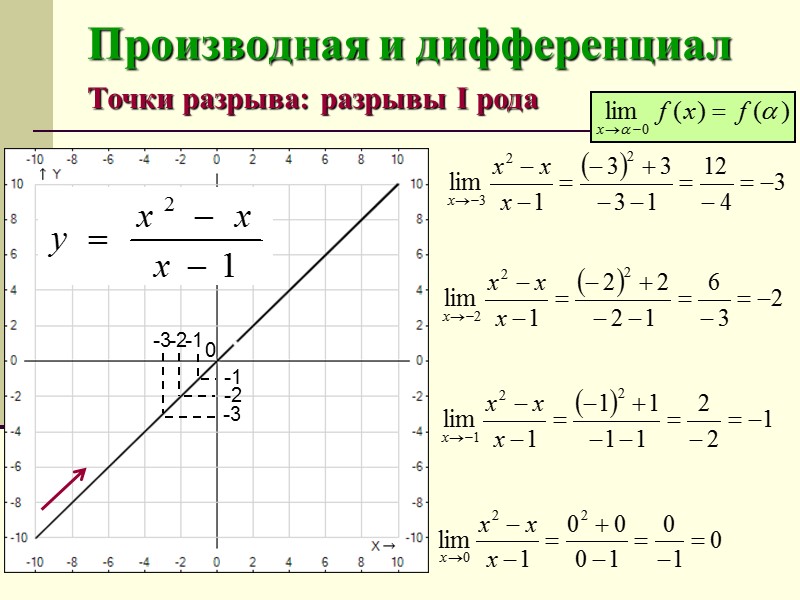
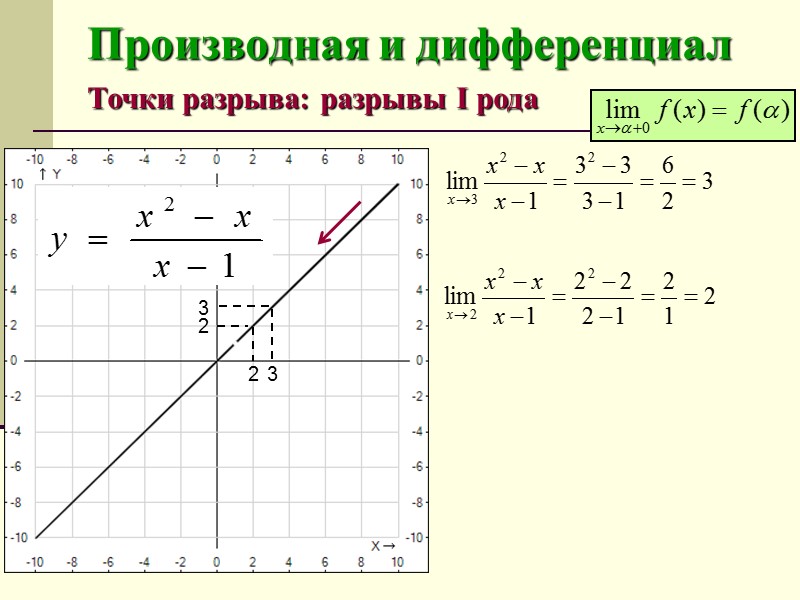
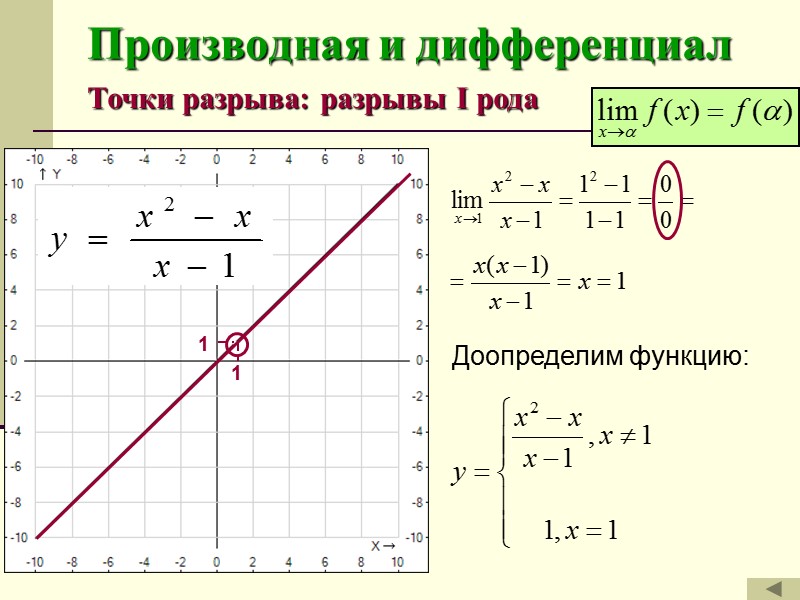
Производная и дифференциал Точки разрыва: разрывы I рода Если функция в точке имеет конечный двусторонний предел, но этот предел отличен от значения функции в этой точке (или точка не входит в область определения функции), то точка называется устранимой точкой разрыва.
Производная и дифференциал Точки разрыва: разрывы I рода -3 -3 -2 -2 -1 -1 0

Производная и дифференциал Точки разрыва: разрывы I рода 3 3 2 2
Производная и дифференциал Точки разрыва: разрывы I рода 1 1 Доопределим функцию:

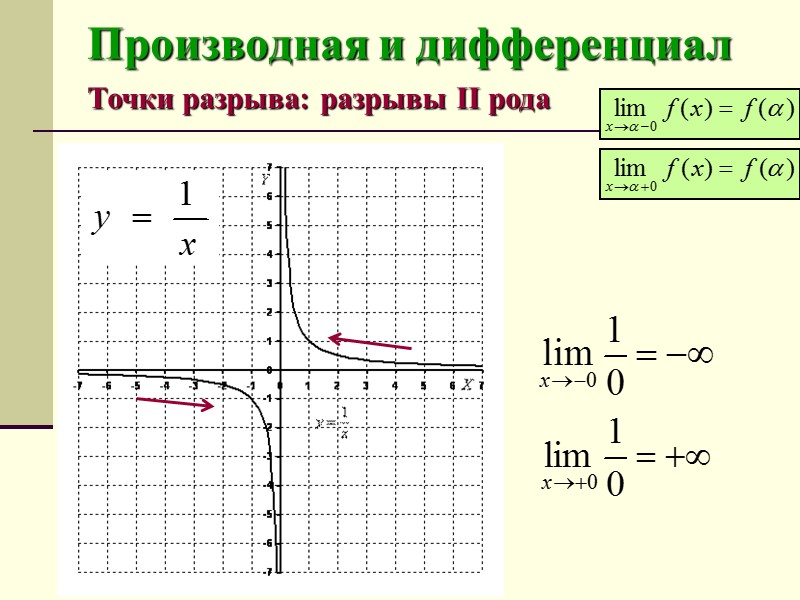
Производная и дифференциал Точки разрыва: разрывы II рода Если функция в точке не имеет конечного левого, правого или обоих пределов, то функция не является неразрывной в точке , и эта точка называется неустранимой точкой разрыва.

Производная и дифференциал Точки разрыва: разрывы II рода
Производная и дифференциал Свойства непрерывности функции Если функции f(x) и g(x) непрерывны в точке , то функция f(x) g(x), f(x)* g(x) и f(x) / g(x) (при условии, что g() ≠ 0) непрерывны в этой точке. Если функция u=g(x) непрерывна в точке и функция y=f(u) непрерывна в точке g(), то сложная функция y=f(g(x)) также непрерывна в точке . Элементарные функции непрерывны в области их определения.
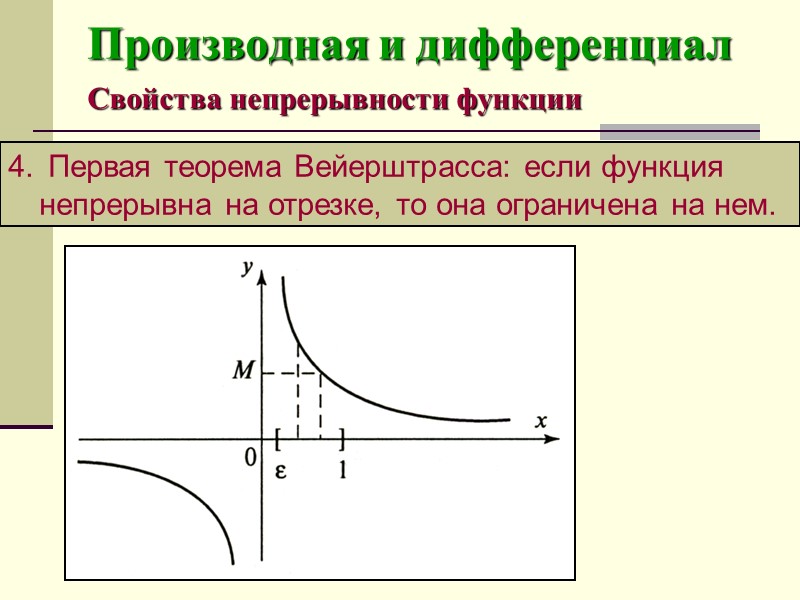
Производная и дифференциал Свойства непрерывности функции Первая теорема Вейерштрасса: если функция непрерывна на отрезке, то она ограничена на нем.

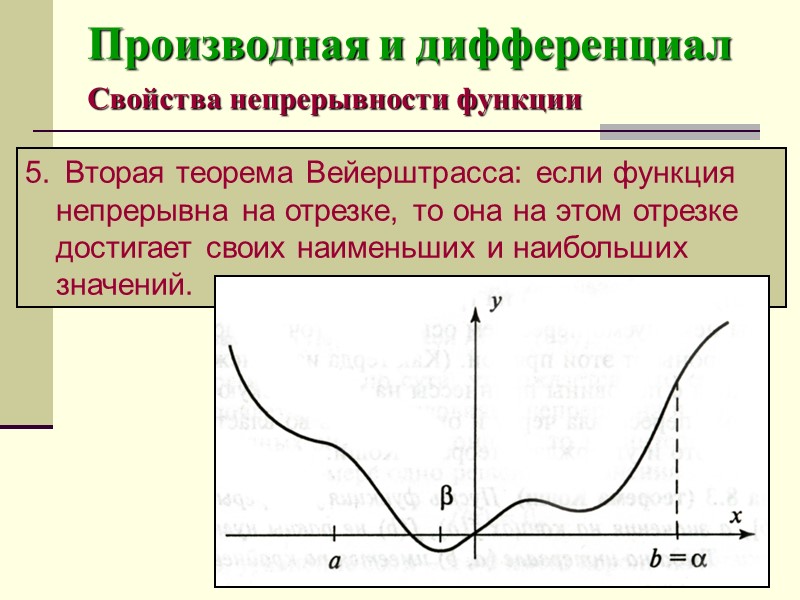
Производная и дифференциал Свойства непрерывности функции Вторая теорема Вейерштрасса: если функция непрерывна на отрезке, то она на этом отрезке достигает своих наименьших и наибольших значений.
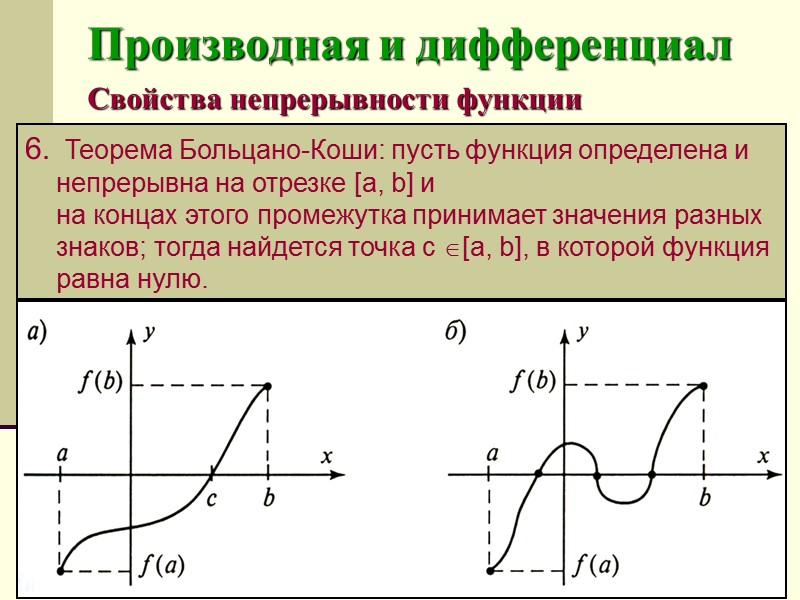
Производная и дифференциал Свойства непрерывности функции Теорема Больцано-Коши: пусть функция определена и непрерывна на отрезке [а, b] и на концах этого промежутка принимает значения разных знаков; тогда найдется точка с [а, b], в которой функция равна нулю.

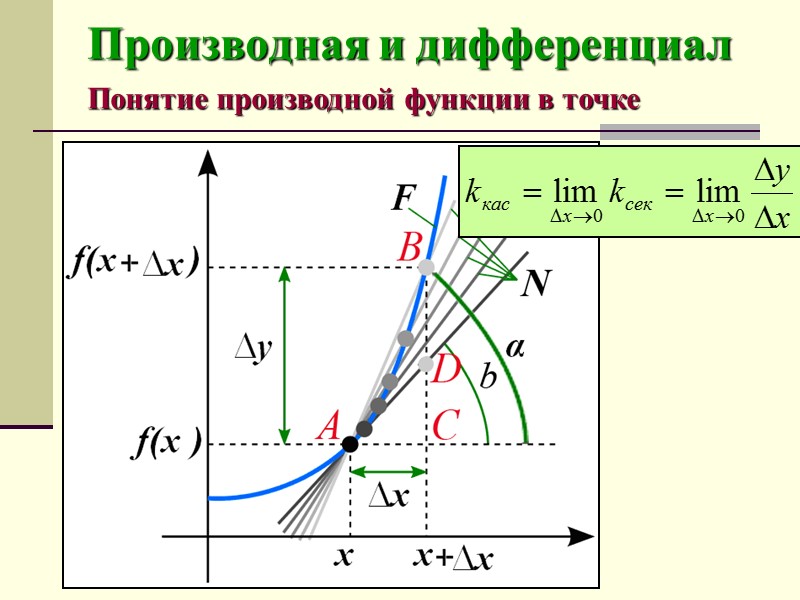
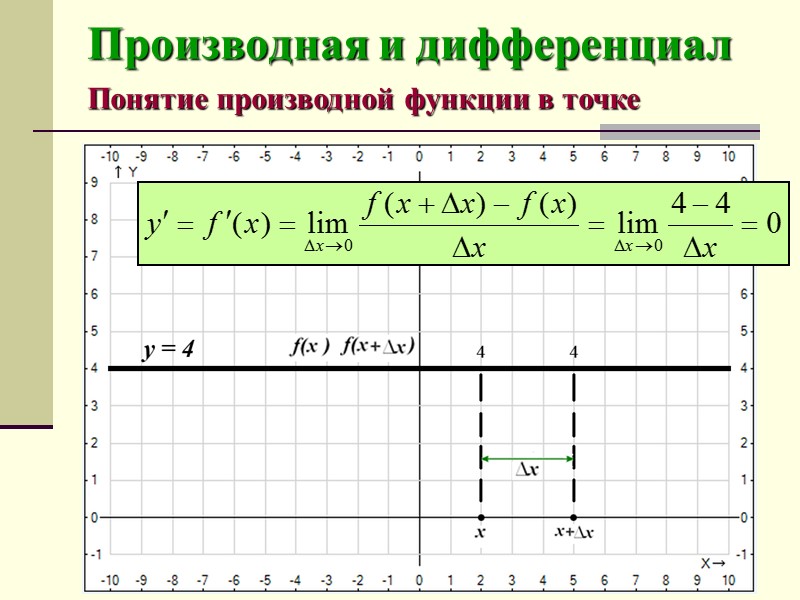
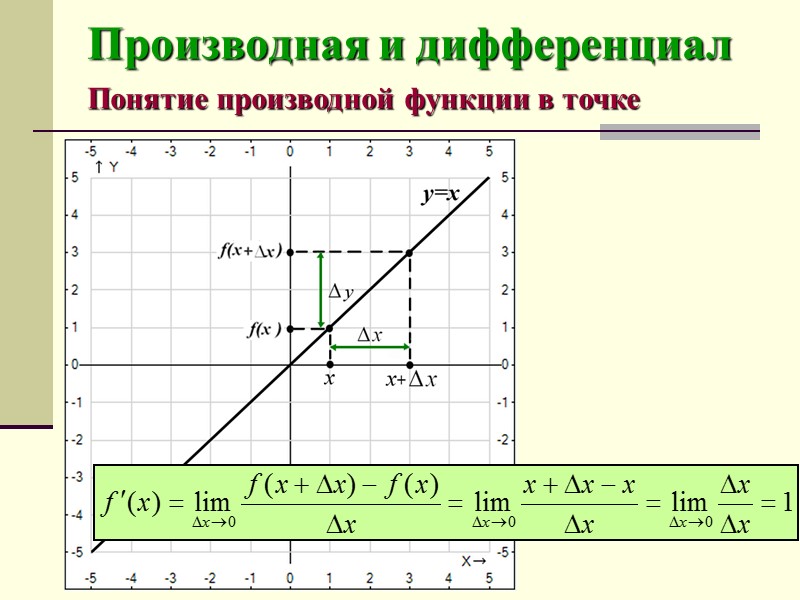
Производная и дифференциал Понятие производной функции в точке Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).

Производная и дифференциал Понятие производной функции в точке

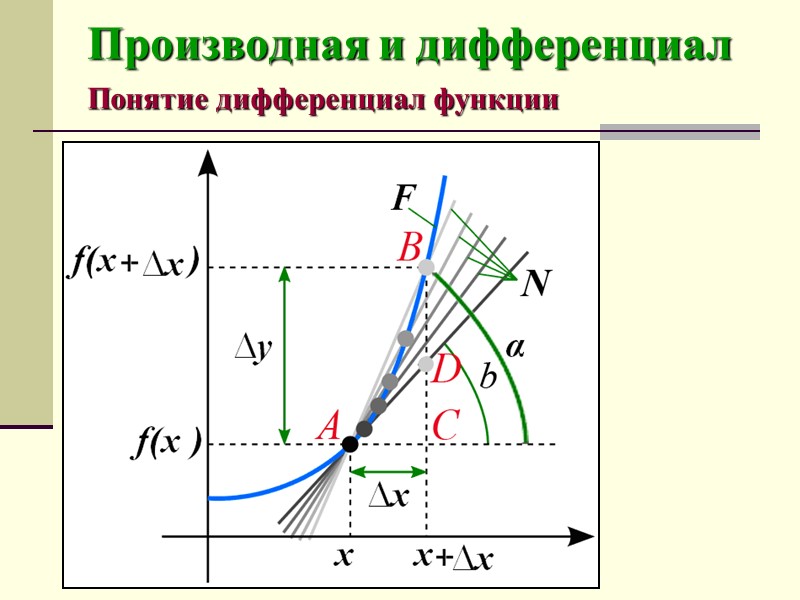
Производная и дифференциал Понятие производной функции в точке Чтобы найти производную f(x) в точке х, необходимо: определить значения этой функции в точке х и в точке x+Δx, где Δx – приращение аргумента х; найти приращение функции Δy = f(x+Δx) – f(x); найти предел (если он существует) отношения приращение функции к приращению аргумента.

Производная и дифференциал Понятие производной функции в точке Предел отношения Δу/Δх=tgВАС(b) tgDАС(а) при Δх 0 (если таковой существует), называется производной функции у = f(x) в точке х.

Производная и дифференциал Понятие производной функции в точке
Производная и дифференциал Понятие производной функции в точке

Производная и дифференциал Понятие производной функции в точке Производная степенной функции: любой радикал (корень) нужно представить в виде для применения формулы Свойства степени
Свойства степени

Производная и дифференциал Понятие производной функции в точке Производная тригонометрических функций у = sin x Используем формулу двойного угла sin2 = 2 sin* cos и организуем первый замечательный предел

Производная и дифференциал Понятие производной функции в точке

Производная и дифференциал Понятие производной функции в точке Производная логарифмических функций у = ln x Используем свойства логарифма и организуем второй замечательный предел

Производная и дифференциал Понятие производной функции в точке

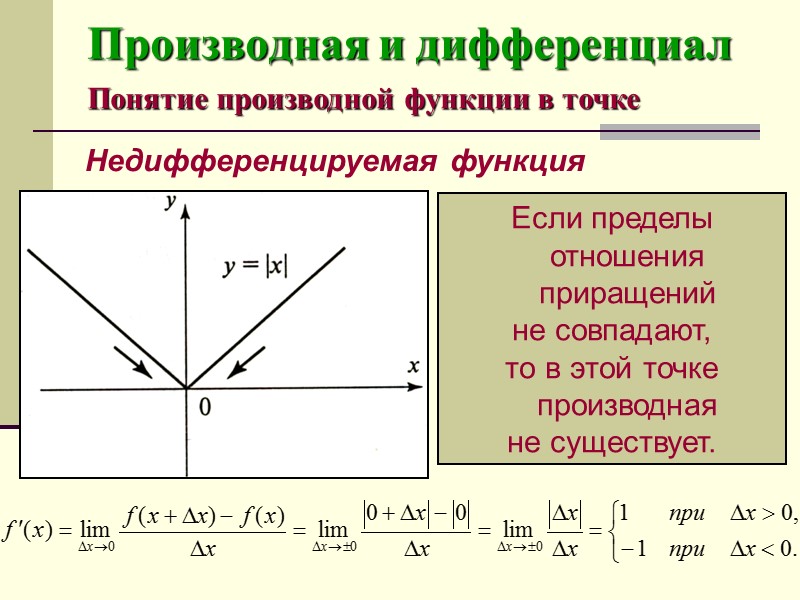
Производная и дифференциал Понятие производной функции в точке Недифференцируемая функция Если пределы отношения приращений не совпадают, то в этой точке производная не существует.

Производная и дифференциал Понятие производной функции в точке Следовательно: если функция прерывна, или имеет изломы в заданной точке (хотя и непрерывна), то она недифференцируема в этой точке; если функция имеет производную в точке, то она непрерывна в этой точке.

Производная и дифференциал Понятие дифференциал функции

Производная и дифференциал Понятие дифференциал функции Δ f f(х)*Δх. Правую часть этого приближенного неравенства называют дифференциалом функции f(х) в точке х и обозначают df(x). df(x)= f(x)*dx

Производная и дифференциал Основные правила дифференцирования

Производная и дифференциал Основные правила дифференцирования Вынесение константы за знак производной Пример. Вычислить производную функции

Производная и дифференциал Основные правила дифференцирования Производная суммы функций Пример. Вычислить производную функции

Производная и дифференциал Основные правила дифференцирования

Производная и дифференциал Основные правила дифференцирования Производная произведения функций Пример. Вычислить производную функции
Производная и дифференциал Основные правила дифференцирования
Производная и дифференциал Основные правила дифференцирования Производная частного функций Пример. Вычислить производную функции
Производная и дифференциал Основные правила дифференцирования

Производная и дифференциал Основные правила дифференцирования Производная сложной функций Пример 1. Вычислить производную функции Определяем внешнюю и внутреннюю (вложенную) функцию: Применяем правило дифференцирования сложной функции:
Производная и дифференциал Основные правила дифференцирования Пример 1. Вычислить производную функции Определяем внешнюю и внутреннюю (вложенную) функцию: Применяем правило дифференцирования степенной функции: Применяем правило дифференцирования сложной функции:

Производная и дифференциал Основные правила вычисления дифференциалов df(x)= f(x)*dx Пример. Вычислить дифференциал функции
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Тема: Производная сложной функции .
Тип урока: – урок изучения нового материала.
Форма урока : применение информационных технологий.
Место урока в системе уроков по данному разделу: первый урок.
научить распознавать сложные функции, уметь применять правила вычисления производных; совершенствовать предметные, в том числе вычислительные, умения и навыки;
развивать логическое и математическое мышление
I. Организационный момент (1 мин.).
II. Постановка целей. Мотивация учащихся (1 мин.).
III. Актуализация опорных знаний (5 мин.).
Дать определение производной функции.
Назовите правила вычисления производной.
3. Устная работа.
Найдите производные функций.
б) f(x) = 3x 2 – 7x + 5;
д) f(x) = (2x – 5)(x + 3).
4. Правила вычисления производных .
Повторение формул по компьютеру со звуковым сопровождением.
IV. Программированный контроль (5 мин.).
Обменяйтесь тетрадями. Отметьте в диагностических картах верно выполненные задания знаком +, а неверно выполненные задания знаком “–”.
V. Изучение нового материала (5 мин.).
Сложная функция.
Рассмотрим функцию, заданную формулой f(x) =
Для того, чтобы найти производную данной функции, надо сначала вычислить производную внутренней функции u = v(x) = xІ + 7x + 5, а затем вычисляют производную функции g(u) = .
Говорят, что функция f(x) – есть сложная функция, составленная из функций g и v , и пишут:
f(x) = g(v(x)) .
Область определения сложной функции – множество всех тех х из области определения функции v , для которых v(x) входит в область определения функции g.
ТЕОРЕМА.
Пусть сложная функция у = f(x) = g(v(x)) такова, что функция у = v(x) определена на промежутке U , а функция u = v(x) определена на промежутке Х и множество всех её значений входит в промежуток U. Пусть функция u = v(x) имеет производную в каждой точке внутри промежутка Х , а функция y = g(u) имеет производную в каждой точке внутри промежутка U. Тогда функция y = f(x) имеет производную в каждой точке внутри промежутка Х , вычисляемую по формуле
y' x = y' u • u' x .
Формулу читают так: производная y по x равна производной y по u
Образовательные: закрепить у учащихся формулы нахождения производных элементарных функций; учить находить производные элементарных функций; выполнить упражнения из ЕГЭ.
Развивающие: развивать коммуникативность, познавательность, способность принимать самостоятельное решение, умение владеть собой.
Воспитательные: создание условий для ситуации успеха, как следствие поддержания интереса к предмету, воспитывать познавательную активность, коммуникативные навыки, мобильность, умения общаться, общей культуры.
Оборудование: мультимидийная презентация, карточки
I Организационный момент
II Актуализация знаний
-Добрый день. Садитесь. Сейчас у нас второй урок на сегоднейший день по расписанию. На первом уроке мы проверили Д.З. по теме, но у нас не проверенные задания по подготовке к ЕГЭ. Домашним заданием было решить уравнения С1 или 15-тригономеррическое. Поднимите руки кто приступал к решению. Опустите. Проверим. Но не просто, в роли эксперта я попрошу выступить Муринову Арину и выставить баллы так же строго как это делаю я.
- Это была вторая часть. По первой части были задания из сборника Ященко по подготовке к ЕГЭ тех заданий в которых ребята нашего класса допустили ошибки при выполнении тренировочного ЕГЭ на профильном уровне № объясняет- , № объясняет, № объясняет.
-Д.З. вы получите в конце урока.
- Но подготовка к ЕГЭ подготовкой, а нам нужно дальше двигаться. Изучение какой темы мы занимаемся.
-А именно производная элементарных функций.
-Вспомним формулы производных элементарных функций.
cos x, cos (кx+в), sin x, sin(кx+в), е х , е кх+в , (а х ) | = а х lnа, ( log a x) | =
III Закрепление полученных знаний
-Найти производную функции. Будем работать в парах.
y=x 3 -2x 2 +е х +3
- Найти ошибку и доказать: 1) y=5x 5 +5е х +3lnх у / =25х 6 +5е х-1 + 2) y=8cos(7-x)+17 sin x-2 у / = -8 sin(7-x)-17cos-2
- В доме, в котором живет Олег, один подъезд. На каждом этаже по пять квартир. Олег живет в квартире 23. На каком этаже живет Олег?
- Держатели дисконтной карты книжного магазина получают при покупке скидку 10%. Книга стоит 480 рублей. Сколько рублей составляет скидка? Ответ разделите на 10 и округлите до едениц.
- Сырок стоит 7 рублей Какое наибольшее число сырков можно купить на 30 рублей?
V Работа по учебнику.
-С целью закрепления выполним задания из учебника.
V Рефлексия Самостоятельная работа по карточкам.
Выставление оценок за работу на уроке. Сравнить с самооценкой.
VI I Домашнее задание: § 47, №840 (4), 841(2,6), 842(2,3,4)
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
- Производная произведения, частного равна ….
- Найти производную функции f(x) = 3х 2 - 5х + 6.
- Найти производную функции f(x) = е 2х + 3lnх + 1.
- Найти производную функции f(x) = (х - 2) 2 cosx .
- Найти производную функции у = (х 2 + 2х)( sin(7-x))
- Найти производную функции у =
По теме: методические разработки, презентации и конспекты

Урок алгебры в 11 классе по теме: "Производная некоторых элементарных функций"
Урок по алгебре 11 класс. Учебник Алгебра и начала анализа под редакцией Ю.М. Колягина. На уроке используются технологии деятельностного подхода. Учащиеся используют на уроке различные информаци.

Карточки- тренажеры по теме " Производные элементарных функций" ( по материалам открытого банка заданий ЕГЭ)
Карточки представлены в двух вариантах. Могут быть исползованы как для отработки навыков, так и для проверочной или домашней работы.
Производные элементарных функций

Самостоятельная работа "Нахождение производных элементарных функций"
Самостоятельная работа "Нахождение производных элементарных функций" на 10 вариантов.

Правила вычисления производной. Производные основных элементарных функций.
Данная презентация может быть использована на уроке для обьяснения нового материала или при повтореннии темы : Производная функции.

Производные некоторых элементарных функций
презентация к уроку, 11 класс.
План-конспект практического занятия "Производные основных элементарных функций"
Раздел 4. Начала математического анализаТема 4.1. Производная и ее применениеЗанятие 34. Производные основных элементарных функций Цель занятия: формирование новых знаний, формирование умений реа.
Читайте также:

