Многоугольники 7 класс геометрия конспект

Обновлено: 05.07.2024

До сих пор в центре нашего внимания был самый простой из многоугольников — треугольник. В этой главе будем изучать более сложные многоугольники, в основном различные виды четырёхугольников: параллелограмм, прямоугольник, ромб, квадрат. Кроме того, в этой главе речь пойдёт о симметрии геометрических фигур, в том числе указанных четырёхугольников. Симметрия играет важную роль не только в геометрии, но и искусстве, архитектуре, технике. В окружающей обстановке мы видим немало симметричных предметов — фасады зданий, узоры на коврах и тканях, листья деревьев.

Рассмотрим фигуру, составленную из отрезков АВ, ВС, CD, . EF, FG так, что смежные отрезки (т. е. отрезки АВ и ВС, ВС и CD, . EF и FG) не лежат на одной прямой. Такая фигура называется ломаной ABCD. FG (рис. 150, а). Отрезки, из которых составлена ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной. Сумма длин всех звеньев называется длиной ломаной. Концы ломаной ABCD . FG, т. е. точки А и G, могут быть различными, а могут совпадать (рис. 150, б). В последнем случае ломаная называется замкнутой, и её звенья FG и АВ также считаются смежными. Если несмежные звенья замкнутой ломаной не имеют общих точек, то эта ломаная называется многоугольником, её звенья называются сторонами многоугольника, а длина ломаной называется периметром многоугольника.

Многоугольник с n вершинами называется n-угольником; он имеет n сторон. Примером многоугольника является треугольник. На рисунке 151 изображены четырёхугольник ABCD и шестиугольник А₁А₂А₃А₄А₅А₆.

Фигура, изображённая на рисунке 152, не является многоугольником, так как несмежные отрезки С₁C₅ и С₂С₃ (а также С₃С₄ и С₁C₅) имеют общую точку.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника.

На рисунке 153 внутренние области многоугольников закрашены. Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.

Выпуклый многоугольник

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

На рисунке 154 многоугольник F₁ является выпуклым, а многоугольник F₂ — невыпуклым.

Рассмотрим выпуклый n-угольник, изображённый на рисунке 155,а. Углы А_nА₁А₂, А₁А₂А₃, . А_n-1А_nА₁ называются углами этого многоугольника. Найдём их сумму.

Для этого соединим диагоналями вершину А₁ с другими вершинами. В результате получим n - 2 треугольника (рис. 155, б), сумма углов которых равна сумме углов n-угольника. Сумма углов каждого треугольника равна 180°, поэтому сумма углов многоугольника АхАг. Аn равна (n - 2) • 180°.

Итак, сумма углов выпуклого п.-угольника равна (n - 2) • 180°.

Внешним углом выпуклого многоугольника называется угол, смежный с углом многоугольника. Если при каждой вершине выпуклого многоугольника А₁А₂ . А_n взять по одному внешнему углу, то сумма этих внешних углов окажется равной

Таким образом, сумма внешних углов выпуклого многоугольника равна 360°.

Четырёхугольник

Каждый четырёхугольник имеет четыре вершины, четыре стороны и две диагонали (рис. 156). Две несмежные стороны четырёхугольника называются противоположными. Две вершины, не являющиеся соседними, также называются противоположными.

Четырёхугольники бывают выпуклые и невыпуклые. На рисунке 156, о изображён выпуклый четырёхугольник, а на рисунке 156, б — невыпуклый.

Каждая диагональ выпуклого четырёхугольника разделяет его на два треугольника. Одна из диагоналей невыпуклого четырёхугольника также разделяет его на два треугольника (см. рис. 156, б).

Так как сумма углов выпуклого n-угольника равна (n - 2) • 180°, то сумма углов выпуклого четырёхугольника равна 360°.

Задачи

363. Начертите выпуклые пятиугольник и шестиугольник. В каждом многоугольнике из какой-нибудь вершины проведите все диагонали. На сколько треугольников разделяют проведённые диагонали каждый многоугольник?

364. Найдите сумму углов выпуклого:

365. Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен:

366. Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4 мм и 5 мм.

367. Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая — в три раза больше второй.

368. Найдите углы выпуклого четырёхугольника, если они равны друг другу.

369. Найдите углы А, В и С выпуклого четырёхугольника ABCD, если ∠A = ∠B = ∠C, a AD = 135°.

370. Найдите углы выпуклого четырёхугольника, если они пропорциональны числам 1, 2, 4, 5.

Краткий курс геометрии 7 класс

☑ 1. Простейшие геометрические фигуры и их свойства

Аксиома. Основное свойство прямой: Через любые две точки можно провести прямую, и притом только одну.
Определение. Пересекающиеся прямые: Две прямые, имеющие общую точку, называют пересекающимися.
ТЕОРЕМА. О двух пересекающихся прямых: Любые две пересекающиеся прямые имеют только одну общую точку.
Два отрезка называют равными, если их можно совместить наложением.
Аксиома. Основное свойство длины отрезка: Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и т. е. АВ = АС + СВ.
Расстоянием между точками называют длину отрезка АВ.
Два луча, имеющие общее начало и лежащие на одной прямой, называют дополнительными.

☑ 2. Углы

Углом называется геометрическая фигура (рис. 1), образованная двумя лучами, исходящими из одной точки.
Точка О — вершина угла, а лучи ОА и ОБ — стороны угла. Обозначение: ∠AOB или ∠ab.
Угол в 90° называется прямым (рис. 2).
Угол, меньший прямого, называется острым (рис. 3).
Угол, больший прямого, но меньший развернутого, называется тупым (рис. 4).

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого (рис. 5).
∠AOC и ∠DOB; ∠BOC и ∠AOD — вертикальные.
Вертикальные углы равны: ∠AOC = ∠DOB и ∠BOC = ∠AOD.
Два угла называются смежными, если у них одна сторона общая, а две другие составляют прямую линию (рис. 6), ∠AOC и ∠BOC — смежные.

Сумма смежных углов равна 180°.
Биссектрисой угла называется луч, проходящий между сторонами угла и делящий его пополам (рис. 7).
Биссектрисы вертикальных углов составляют продолжение друг друга (рис. 8).
Биссектрисы смежных углов взаимно перпендикулярны (рис. 9).

При пересечении двух прямых a и b третьей с (секущей) образуется 8 углов (рис. 10):

соответственные углы: ∠1 и ∠5, ∠2 и ∠6, ∠4 и ∠8, ∠3 и ∠7;
внутренние накрест лежащие: ∠4 и ∠6, ∠3 и ∠5;
внешние накрест лежащие: ∠1 и ∠7, ∠2 и ∠8;
внутренние односторонние: ∠4 и ∠5, ∠3 и ∠6;
внешние односторонние: ∠1 и ∠8, ∠2 и ∠7.

☑ 3. Параллельные прямые

Две прямые называют параллельными, если они не пересекаются.
Аксиома параллельности прямых: Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Признаки параллельности двух прямых:
• Две прямые, перпендикулярные третьей прямой, параллельны.
• Если накрест лежащие углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
• Если сумма односторонних углов, образующихся при пересечении двух прямых секущей, равна 180°, то прямые параллельны.
• Если соответственные углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
Свойства параллельных прямых:
• Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.
• Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.
• Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180°.
Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

☑ 4. Треугольник

Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, последовательно соединяющих эти точки.
Точки А, В, С — вершины треугольника АВС.
Отрезки АВ, ВС и АС — стороны, ∠A, ∠B и ∠C — углы. ∠A + ∠B + ∠C = 180°.
Стороны треугольника часто обозначают малыми буквами (рис. 13): АВ = с, ВС = а, АС = b.
Р = а + b + с — периметр треугольника.

Треугольник, у которого все углы острые, называется остроугольным (см. рис. 13).
Треугольник, у которого есть прямой угол, называется прямоугольным (рис. 14).
Стороны, образующие прямой угол, называются катетами (а и b), а сторона, лежащая против прямого угла, — гипотенузой (с).
Треугольник с тупым углом называется тупоугольным (рис. 15).

Треугольник, у которого две стороны равны, называется равнобедренным (рис. 16).
Равные стороны называются боковыми, а третья сторона — основанием равнобедренного треугольника.
Треугольник, у которого все стороны равны, называется равносторонним (рис. 17).
Каждый угол равностороннего треугольника равен 60°.
Свойства равнобедренного треугольника:
1. Углы при основании равны.
2. Биссектриса, проведенная к основанию, является одновременно медианой и высотой.
3. Высота, проведенная к основанию, является одновременно медианой и биссектрисой.
4. Медиана, проведенная к основанию, является одновременно высотой и биссектрисой.

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника (рис. 18). ∠CBD — внешний угол треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним (см. рис. 18): ∠CBD = ∠A + ∠C.
Отрезок, соединяющий середины двух сторон, называется средней линией треугольника (рис. 19).

☑ 5. Признаки равенства треугольников

I признак (признак равенства по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 20). АВ = А₁В₁, АС = А₁С₁, ∠A = ∠A₁

II признак (признак равенства по стороне и прилежащим к ней углам).
Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 21). АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁

III признак (признак равенства по трем сторонам).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 22). АВ = А₁В₁, ВС = B₁C₁, АС =А₁С₁.

Вы смотрите:
Краткий курс геометрии 7 класс

☑ 6. Соотношения между сторонами и углами треугольника

ТЕОРЕМА о сумме углов треугольника. Сумма углов треугольника равна 180°. ∠A + ∠B + ∠C = 180°.
ТЕОРЕМА о соотношениях между сторонами и углами треугольника. В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.
Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.
Следствие 2. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
ТЕОРЕМА о неравенстве треугольника. Каждая сторона треугольника меньше суммы двух других сторон: а ☑ 7. Определение вида треугольника по его сторонам

Пусть с — наибольшая сторона, тогда:
а) если с 2 2 + b 2 , то треугольник остроугольный;
б) если с 2 > а 2 + b 2 , то треугольник тупоугольный;
в) если с 2 = а 2 + b 2 , то треугольник прямоугольный.

☑ 8. Прямоугольные треугольники (некоторые свойства)

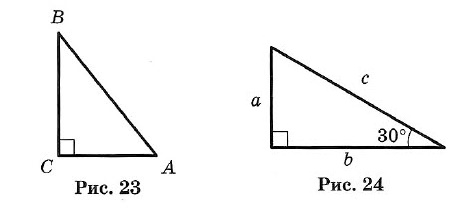
1. Сумма острых углов равна 90° (рис. 23). ∠A + ∠B = 90°.
2. Катет, лежащий против угла в 30°, равен половине гипотенузы (рис. 24). a = c/2
3. Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° (рис. 24).

☑ 9. Признаки равенства прямоугольных треугольников

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис. 25). АС = А₁С₁, ВС = В₁С₁.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны (рис. 26). АС = А₁С₁, ∠A = ∠A₁.

3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны (рис. 27). АВ = А₁В₁, ∠A = ∠A₁.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис. 28). АВ = А₁В₁, АС = А₁С₁

Краткий курс геометрии 7 класс

☑ 10. Четыре замечательные точки треугольника

С каждым треугольником связаны 4 точки:
1) точка пересечения медиан;
2) точка пересечения биссектрис;
3) точка пересечения высот (или их продолжений);
4) точка пересечения серединных перпендикуляров к сторонам.
Эти четыре точки называются замечательными точками треугольника.
Высотой треугольника называется длина перпендикуляра, опущенного из любой его вершины на противолежащую сторону или ее продолжение.

В тупоугольном треугольнике (рис. 29) две высоты падают на продолжение сторон и лежат вне треугольника, а третья внутри.
В остроугольном треугольнике (рис. 30) все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты одновременно служат и высотами (рис. 31).
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном треугольнике он совпадает с вершиной прямого угла.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Три медианы треугольника пересекаются в одной точке, которая является центром тяжести треугольника (рис. 32).
Эта точка делит каждую медиану в отношении 2 : 1 (считая от соответствующей вершины).
Биссектрисой треугольника называется отрезок биссектрисы угла от вершины до пересечения с противолежащей стороной.
Три биссектрисы треугольника пересекаются в одной точке, которая является центром вписанного круга (рис. 33).
Три перпендикуляра к сторонам треугольника, проведенные через их середины (рис. 34, 35, 36), пересекаются в одной точке, которая является центром описанной окружности.

В тупоугольном треугольнике (рис. 34) эта точка лежит вне треугольника, в остроугольном (рис. 35) — внутри, в прямоугольном — на середине гипотенузы (рис. 36).
Ортоцентр, центр тяжести, центр вписанной и описанной окружностей совпадают друг с другом только в равностороннем треугольнике.

☑ 11. Окружность

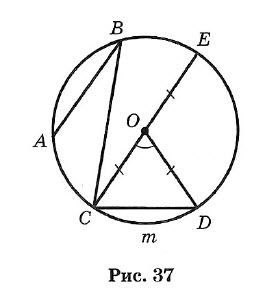
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R. На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр. Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

☑ 12. Свойства касательных к окружности

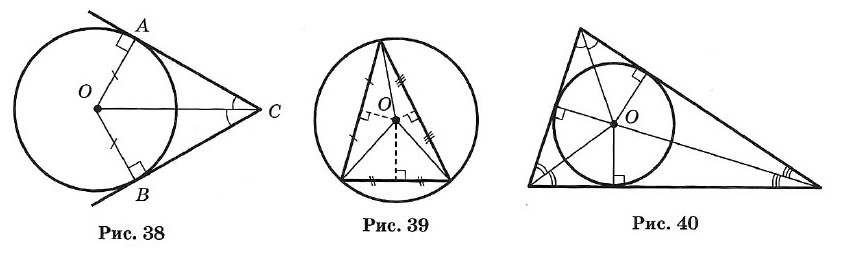
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.

☑ 13. Окружность и треугольник

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Муниципальное общеобразовательное автономное учреждение

средняя общеобразовательная школа №15

городского округа г. Нефтекамск РБ

Учитель математики Давлетгареева И.Н.

11 декабря 2018г.

Тип урока: урок применения и совершенствования знаний и умений.

Цель темы – расширить и систематизировать знания учащихся о правильных многоугольниках.

Образовательная: создать условия для закрепления учащимися основных формул (вычисления площадей и сторон правильных многоугольников; радиусов вписанных и описанных окружностей) и применения этих формул для решения практических задач.

Развивающая: развивать логическое мышление учащихся посредством использования логических операций: сравнения, обобщения, анализа и синтеза при решении задач различными способами; развивать навыки самоконтроля и взаимоконтроля, формировать ключевые компетенции учащихся .

Воспитательная: способствовать воспитанию трудолюбия, умения преодолевать трудности при достижении цели, умения работать в группе.

Методы обучения: сочетание проблемно-эвристического, частично поискового и исследовательского, репродуктивного, т ехнология личностно-ориентированного обучения.

Оборудование: мультимедийная доска, раздаточный материал: конверты, карточки разрезные, индивидуальные таблицы, индивидуальные магнитные доски.

2. Определение темы урока по ребусу - 3 балла. (Правильные многоугольники) - 2 минуты. Проблемно-эвристический метод.

- Какой многоугольник называется выпуклым?

- Какой многоугольник называется правильным?

- Какой треугольник является правильным? Почему?

- Является ли правильным четырехугольником прямоугольник? Почему?

- Является ли правильным четырехугольником ромб?

- Является ли правильным четырехугольником квадрат?

5. Проблемная беседа – 10 минут. Учащимся предлагается найти применение правильным многоугольникам в жизни. Оценивается активность в беседе до 3 баллов

- Где вы могли видеть правильные многоугольники?

1 ) Паркет – это покрытие плоскости многоугольниками без пропусков и наложений.

- Из каких правильных многоугольников можно построить правильный паркет?

- Какое н еобходимое условие для построения паркета? (в узле 360 градусов)

2) Пчелиные соты

Сос тоят из множества шестигранных ячеек. Такое строение сот придает им необходимую прочность, кроме того, шестигранная форма ячеек требует наименьших затрат строительного материала (воска). На постройку одной пчелиной ячейки уходит около 13 мг воска, на постройку всего сота – 140-150 граммов.

То, что творит архитектор – пчела поистине уникально. Энергетическое строение Вселенной сегодня изучается квантовыми физиками, и оно идеально соответствует строению восковых сот.

А знаете ли Вы, что если на вощине сделать угол шестигранника на несколько тысячных радиан больше или меньше, то пчела сгрызет до основания этот участок и перестроит заново.

3) Сечение гайки, болта и многих технических деталей, карандашей имеет вид правильного шестиугольника.

4) Некоторые сложные молекулы углерода (например, графит) имеет гексагональную кристаллическую решетку.

5) Из лоскутков тканей можно изготовить своими руками покрывала, наволочки, коврики, одеяла .

6. Дифференцированная работа – 27 минут.

каждый его внутренний угол равен 60°,90°, 120°;

каждый его внешний угол равен 120°,90°, 60°;

из каждой вершины многоугольника можно провести две диагонали;

из каждой вершины можно провести три диагонали, две из которых равны между собой;

центральный угол равен 60°,90°, 120°;

все его диагонали равны;

середины правильного 12- угольника соединили через одну;

сумма внешних углов равна 360°;

сумма его внутренних углов равна сумме его внешних углов;

каждый его внутренний угол равен центральному углу;

вершины правильного 8 - угольника соединили отрезками через одну;

равны все внутренние углы многоугольника.

Задача Жители села решил разбить клумбу в парке отдыха. Клумба имеет вид правильного шестиугольника без правильного треугольника, вершины которого совпадают с вершинами шестиугольника. Сторона шестиугольника 6 метров. Вычислите площадь этой клумбы. Определите плату за вскапывание клумбы, если за вскапывание 1 кв. м земли надо платить 30 рублей. (7 баллов)

Задача 1. Найдите углы правильного восьмиугольника.

Задание 2. Постройте правильный восьмиугольник, двенадцатиугольник .

Сегодня на уроке:

- Мы повторили _________; - Мы закрепили умения _________; - Теперь я могу _______________.

9. Постановка домашнего задания – 2 минуты. (Технология личностно-ориентированного обучения)

Задание ученики выбирают по желанию из предложенных:

2)Изготовить узор, паркет, др. из правильных многоугольников.

10 . Рефлексия – 2 минуты . Что понравилось на уроке? На каких этапах урока чувствовал себя уверенно? Определи своё настроение (поднимают фигуру определённого цвета). С чем это связано? Какие вы сделали выводы по усвоению данной темы?

ОПРЕДЕЛЕНИЯ

Ломаная А₁А₂А₃…А_n — фигура, состоящая из точек А₁, А₂, А₃, …, А_n и отрезков А₁А₂, А₂А₃, …, А_n-1А_n, которые их соединяют. Точки А₁, А₂, А₃, …, А_n называют вершинами ломаной, а отрезки А₁А₂, А₂А₃, …, А_n-1А_n — звеньями ломаной.

Простая лoманая — лoманая, не имеющая точек самопересечения.
Замкнутая лoманая — лoманая, концы которой соединяются.
Длина ломаной — сумма длин ее звеньев.

Многоугольник — простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой; вершины ломаной называют вершинами многоугольника, а звенья ломаной — сторонами многоугольника. Многоугольник с n вершинами (n сторонами) называют n-угольником.

Диагональ многоугольника — отрезки, соединяющие несоседние вершины многоугольника.
Выпуклый многoугольник — многоугoльник, лежащий в одной полуплоскости относительно любой прямой, содержащей его сторону.
Угол выпуклого многоугольника при данной вершине — угол, образованный его сторонами, сходящимися в этой вершине.
Внешний угол выпуклого многоугольника при данной вершине — угол, смежный с внутренним углом многоугольника при этой вершине.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Задача № 1. Дано: ABCD — четырехугольник; ∠A = ∠B = ∠C; ∠D = 135.
Найти: ∠A, ∠B, ∠C.

Задача № 2. Дано: ABCDE — четырехугольник; ∠A : ∠B : ∠C : ∠D : ∠E = 1 : 2 : 3 : 4 : 8. Найти: ∠A, ∠B, ∠C, ∠D, ∠E.

Читайте также: