Графы решение задач с помощью графа конспект
Обновлено: 20.05.2024
Автор: Каракозова Марина Анатольевна
Должность: учитель математики
Учебное заведение: МБОУ СОШ р.п.Жадовка МО "Барышский район"
Населённый пункт: р.п.Жадовка
Наименование материала: Методическая разработка внеурочного занятия
Тема: "Решение логических задач с помощью графа"
Раздел: среднее образование
Предметные
: развитие представления о графах как вспомогательных средствах при решении задач;
Метапредметные
: формирование умения выделять существенные признаки объекта и отношения между объектами; умение строить схемы;
Личностные
: формирование способности увязать учебное содержание с собственным жизненным опытом, понять значение информационного моделирования как метода познания окружающей действительности. В ходе занятия у учащихся могут быть сформированы универсальные учебные действия:
Регулятивные УУД.
Обнаружить и сформулировать учебную проблему, составить план выполнения работы
Познавательные
УУД.
Общеучебные действия: поиск и выделение необходимой информации, самостоятельное создание алгоритмов деятельности. Логические действия: построение логической цепи рассуждений.
Коммуникативные
УУД.
Умение с достаточной полнотой и точностью выражать свои мысли, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Ход занятия. В Википедии можно найти следующее определение графа. В общем смысле
граф
представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара
м н о ж е с т в . Те о р и я г р а ф о в н а ход и т п р и м е н е н и е , н ап р и м е р , в геоинформационных системах ( Г И С ) . Су щ е с т ву ю щ и е и л и в н о в ь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут. Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез. Но с помощью графов можно решать логические задачи различной тематики. Рассмотрим некоторые из них.
№ 1.
В первенстве класса по шашкам было 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Каждый участник должен сыграть по одной партии друг с другом. К настоящему моменту некоторые партии уже сыграны: Андрей сыграл с Борисом, Галиной и Еленой; Борис с Андреем, Галиной; Виктор - с Галиной, Дмитрием и Елена – с Андреем и Виктором. Сколько игр проведено и сколько осталось провести? Решение: 1. Изобразим точки с начальными буквами имен всех участников. 2. Соединим отрезками те точки – игроков, которые уже сыграли (голубые). 3. Посчитаем количество получившихся отрезков – игр. (7) 4. Соединим другим цветом тех игроков, которые еще не играли.(красные) 5. Посчитаем количество получившихся отрезков – несыгранных игр. (8)
№ 2
Актуальность. Основной задачей школы является не подача детям большого объёма знаний, а обучение учащихся самим добывать знания, умению перерабатывать эти знания и применять их в каждодневной жизни. Поставленные задачи может решить ученик, обладающий не только умением хорошо и много работать, но и ученик с развитым логическим мышлением. В связи с этим во многие школьные предметы вложены различного типа задачи, которые и развивают у детей логическое мышление. Решая эти задачи, мы применяем различные приёмы решения. Одни из приёмов решения – это граф.
Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов. Толчок к развитию теория графов получила на рубеже XIX и XX столетий, когда резко возросло число работ в области топологии и комбинаторики, с которыми её связывают самые тесные узы родства. В последнее время графы и связанные с ними методы исследований пронизывают на разных уровнях едва ли не всю современную математику. Графы используются в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине. Как более жизненный пример можно взять использование графов в геоинформационных системах. Существующие или вновь проектируемые дома, сооружения, кварталы и т.п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т.п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут. Теория графов быстро развивается, находит всё новые приложения и ждёт молодых исследователей.
Ход урока
Организационный момент
Актуализация знаний
Опрос учащихся. Решение простых задач.
Что такое граф, ребра?
Граф – это конечное множество точек, некоторые из которых соединены линиями.
Точки – называются вершинами, а соединяющие их линии – ребрами.
- Давайте посчитаем сколько в полученном графе вершин и ребер.
Число ребер, выходящих из каждой вершины графа мы будем называть степенью этой вершины.
Если из вершины выходит нечетное число ребер – она будет называться нечетной, а если четное – четной.
- Назовите, пожалуйста, сколько ребер выходит из каждой вершины и назовите степень вершины каждого графа (дети отвечают на поставленный вопрос)
- Что же нам необходимо сделать, чтобы решить эту задачу?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
- Опять, что мы с вами нарисовали?
Задача №2. Допустим, что у вас в понедельник 4 урока: русский язык, математика, история и технология. Сколькими способами можно составить расписание из 4 предметов, если первым уроком должна быть математика и предметы не повторяются.
- Как же нам можно решить эту задачу?
(Выслушиваются ответы детей).
Доклад учащегося. (историческая справка)

- У меня в руках 2 картинки: домик и прямоугольник, в котором проведены диагонали.
У вас на листочках эти фигуры. Ваша задача: выяснить, можно ли нарисовать эти фигуры, не отрывая карандаш от листа.
Кто смог нарисовать эти фигуры?
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Такими графы названы в честь учёного Леонарда Эйлера.
Объявление темы урока
Скажите, пожалуйста, а как можно использовать графы при решении задач?
Изучение нового материала
Сколько существует трёхзначных чисел, состоящих из цифр 1 и 2?
Граф задачи о переправе
Задача. На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Вершины графа - это деревья, обозначенный первой буквой названия дерева. В данной задача два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

Динамическая пауза: физкультминутка
Закрепление изученного материала
Ниже представлен разбор задач.


Домашнее задание. §1.3.
Рефлексия
Подготавливаются смайлики, которые учащиеся показывают учителю и одноклассникам, с каким настроением они закончили урок.

Урок для развития познавательного интереса на уроках математики.
Технологическая карта урока математики в 7 классе
ФИО Воробьева Елена Валерьевна
Должность учитель математики
Формы работы: групповая
Тип урока: урок открытия новых знаний.
Деятельностная: научить детей новым способам нахождения знания, ввести новые понятия, термины, правила; узнав новые термины и правила, попытаться на уроке реализовать эти знания, применить их на практике.
Содержательная: сформировать систему новых понятий, расширить знания учеников за счет включения новых определений, терминов, описаний, познакомиться со знаменитой задачей о семи мостах Кенигсберга Леонарда Эйлера, попробовать решить ее опытным путем, применить знания при решении задач с помощью графов.
Задачи урока:
образовательные: познакомиться с теорией графов; с решением задач с использованием графов;
развивающие: развитие коммуникативности, навыков само- и взаимоконтроля, математического и общего кругозора, мышления, речи, внимания, памяти, умения анализировать, сравнивать, обобщать;
воспитательные: формирование положительной мотивации и интереса к математике, потребности в приобретении новых знаний; воспитание активности, умения общаться, сотрудничать и работать в группах, воспитание общей культуры.
Планируемые результаты:
Метапредметные:
Коммуникативные: способствовать формированию научного мировоззрения.
Регулятивные: планировать свое действие в соответствии с поставленной задачей.
Познавательные: анализировать результаты элементарных исследований, фиксировать их результаты, развивать умение структурировать полученные знания.
Личностные: формирование и развитие творческих способностей через активные формы деятельности
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Необходимое оборудование: асфальт, мел, раздаточный материал, листы самооценивания.
Структура урока
Основные этапы урока
Задачи этапа
Деятельность учителя
Деятельность ученика
Методы обучения
Прогнозируемый результат
Учебно-методическое обеспечение
Психологическая подготовка к общению
Обеспечивает благоприятный настрой.
Настраиваются на работу дети
Заинтересовать и подготовить к введению нового понятия
Организует работу обучающихся, контролирует правильность выполнения заданий
Опытным путем находят фигуры, которые можно обвести не прерывая линию
Правильно выполненное задание, коррекция ошибок
Выполняют задание на асфальте, работа в группах
Этап осуществление первого пробного действия
Создать проблемную ситуацию
Создает проблемную ситуацию, объясняет учебную задачу, наблюдает, консультирует
Предлагают пути решения проблемы,
осуществление первого пробного действия
Проблема с выполнением задания
Работа в группах
Разработка проекта, плана по выходу их создавшегося затруднения. Реализация выбранного плана по разрешению затруднения.
Обеспечить деятельность по решению задачи
Рассмотрение множества вариантов, поиск оптимального решения
Работа в группах
Первичное закрепление нового знания
Применение новых знаний при решении задач
Предлагает выполнить новое задания по группам
Контроль и самопроверка знаний
Выявить качество усвоения материала
Предлагает проверить задания
Проверяют задания по группам
Информация о домашнем задании
Обеспечить понимание содержания домашнего задания
Поясняет домашнее задание
Записывают домашнее задание
Домашнее задание в листах самоконтроля
Подведение итогов. Рефлексия
Дать оценку работы класса
Подводит итоги урока, ставит задачи на следующий урок
Заполняют листы самоконтроля
Осмысление результатов своей работы
Самоанализ урока математики в 7 классе
Урок разрабатывался в соответствии с психолого-педагогическими характеристиками, состоянием развития общеучебных умений, индивидуальными особенностями учащихся, способных осваивать учебный материал школьной программы по математике.
Класс повышенной активности, любознательный. Ребята были готовы к восприятию новой темы, с большим удовольствием работали на уроке в нестандартной обстановке – на улице, чертили на асфальте разноцветными мелками. Выбранный тип урока соответствовал поставленной цели. Структура урока соответствовала его типу. Между этапами урока существовали взаимные связи, каждый последующий этап являлся продолжением предыдущего этапа. Применяемые методы обучения: частично-поисковый, проблемное изложение, исследовательский. Формы работы: фронтальная и групповая.
На уроке были использованы активные методы обучения - мозговой штурм. Стиль отношений с учащимися активно-положительный. Ученики на уроке работали все, были более или менее активные, пассивных не было. Во время урока большая нагрузка легла на плечи учащихся, учитель выступал в качестве координатора.
На уроке были использованы современные образовательные технологии: проблемное обучение – на этапе мотивации учащихся, групповая работа, здоровьесберегающая технология (урок на свежем воздухе, плюс в течение урока учащиеся постоянно находились в движении).
• решить поставленные задачи урока и получить соответствующие им результаты обучения;
• избежать перегрузки и переутомления учащихся;
• сохранить и развить продуктивную мотивацию учения, настроение, самочувствие.
Удалось полностью реализовать все поставленные задачи; выполнили все планируемые задания; пройдены все этапы урока ОНЗ.
Организационный момент
Мотивационный этап
Перед вами фигуры, попробуйте обвести их, не отрывая мелка, не проводя по одной линии дважды. Выберите те фигуры, которые можно обвести одним росчерком.
(Каждая группа работает самостоятельно. Фигуры изображены на асфальте.)



Какие фигуры не получилось обвести? Есть ли варианты – почему не получилось обвести?(обсуждаются варианты, если есть).
Для решения задач, подобных этой, существуют признаки, по которым заранее не сложно установить, можно ли данную фигуру начертить одним росчерком или нет. Если можно, то с какой точки следует начинать вычерчивание? Изучением этих признаков занимается наука Топология -это раздел математики, изучающий такие свойства фигур, которые не меняются при деформациях, производимых без разрывов и склеивания. Например, с точки зрения топологии, круг, эллипс, квадрат и треугольник обладают одинаковыми свойствами и являются одной и той же фигурой, так как можно деформировать одну в другую, а вот кольцо к ним не относится, так как, чтобы его деформировать в круг, необходима склейка.
Получаем следующие признаки вычерчивания фигур одним росчерком:
а) если нечетных точек в фигуре нет, то ее можно начертить одним росчерком, начиная вычерчивать с любого места;
б) если в фигуре две нечетные точки (если фигура имеет нечетную точку, то она всегда имеет и вторую нечетную точку), то ее можно начертить одним росчерком, начав вычерчивание в одной из нечетных точек и закончив в другой;
в) если в фигуре более двух нечетных точек, то ее нельзя вычертить одним росчерком.
Вместе с обучающимися считаем количество узлов каждой фигуры и находим ответ можно или нет обвести ее одним росчерком.
Такие фигуры (состоящие из точек и линий) называют Графами.
Этап осуществления первого пробного действия
Только что приобретенные вами знания имеют порой любопытное применение.
Город Кенигсберг (после мировой войны он называется Калининград) стоит на реке Преголь. Некогда там было 7 мостов, которые связывали между собой берега и два острова. Жители города заметили, что они никак не могут совершить прогулку по всем семи мостам, пройдя по каждому из них ровно один раз. Так возникла головоломка: “можно ли пройти все семь кенигсбергских мостов ровно один раз и вернуться в исходное место?”.

Этап разработки проекта, плана по выходу их создавшегося затруднения.
Попробуйте и вы, может у кого-нибудь получится.
В 1735 году эта задача стала известна Леонарду Эйлеру. Эйлер выяснил, что такого пути нет, т. Е. доказал, что эта задача неразрешима. Конечно, Эйлер решил не только задачу о кенигсбергских мостах, а целый класс аналогичных задач, для которых разработал метод решения. Можно заметить, что задача состоит в том, чтобы по карте провести маршрут – линию, не отрывая карандаша от бумаги, обойти все семь мостов и вернуться в начальную точку. Поэтому Эйлер стал рассматривать вместо карты мостов схему из точек и линий, отбросив мосты, острова и берега, как не математические понятия. Вот что у него получилось:

А, В – острова, M, N – берега, а семь кривых – семь мостов.
Теперь задача такая – обойти контур на рисунке так, чтобы каждая кривая проводилась ровно один раз. То есть – можно ли обвести этот граф одним росчерком?
Докажем неразрешимость нашей задачи. Как видим, в нашем графе все вершины нечетные.
Этап первичного закрепления нового знания
Каждая группа получает карточку с задачами. Решить с помощью графов.
Пятеро ученых, участвовавших в научной конференции, обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Ответ: Каждое ребро графа – одно рукопожатие. 10 рукопожатий.
На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

В данном видеоуроке мы выясним, что называют графом. Узнаем, что называют вершинами и рёбрами графа. Научимся решать задачи с помощью графов.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Решение задач с помощью графов"
Давайте выясним понятие графа на примере решения задачи.
В первенстве класса по настольному теннису шесть участников: Андрей, Саша, Вова, Оля, Дима и Лена. Каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Сашей, Олей и Леной; Саша, как уже говорилось, с Андреем и ещё с Олей; Вова – с Олей, Димой и Леной. Сколько игр уже проведено и сколько ещё осталось?
Итак, изобразим данные этой задачи в виде схемы. Участников первенства обозначим точками, расположив их по окружности: Андрей – А, Саша – ЭС, Вова – ВЭ, Оля – О, Дима – ДЭ, Лена – ЭЛЬ.

Если двое участников уже сыграли между собой, то будем соединять, обозначающие их точки отрезками. В условии задачи сказано, что Андрей сыграл с Сашей, Олей и Леной.

Мы уже видим, что Саша сыграл с Андреем, а ещё он сыграл с Олей.

Вова сыграл с Олей, Димой и Леной.

Получившаяся схема называется графом. Точки А, С, В, О, ДЭ, Л называются вершинами графа. Отрезки, которые соединяют вершины графа, называются рёбрами графа. Каждое ребро соединяет две вершины графа.
При этом обратите внимание, что точки, в которых пересекаются рёбра графа, не являются его вершинами.

У графа 7 рёбер. Это означает, что к настоящему моменту было проведено 7 игр.
Чтобы найти количество игр, которые осталось провести, продолжим построение этого графа так, чтобы из каждой точки были проведены рёбра ко всем остальным точкам. Но для того, чтобы потом легче было подсчитать количество добавленных рёбер, рисовать их будем другим цветом.
Итак, известно, что Андрей сыграл с Сашей, Олей и Леной. А значит, он не играл с Вовой и Димой.

Также известно, что Саша сыграл с Андреем и с Олей, а значит, он не сыграл с Вовой, Димой и Леной.

Вова сыграл с Олей, Димой и Леной. Получается, что он не сыграл с Андреем и Сашей. Но соответствующие отрезки уже проведены.
Оля сыграла с Андреем и Сашей, а также с Вовой. Это значит, что она ещё не сыграла с Димой и Леной.

Дима сыграл только с Вовой. Ему предстоит сыграть с Олей, Сашей и Андреем, но эти отрезки мы уже провели. Осталось провести отрезок от Димы к Лене.

Лена сыграла с Андреем и Вовой. Ей предстоит сыграть с Димой, Олей и Сашей, но эти отрезки мы уже провели. Больше ничего добавлять не надо.
Мы добавили 8 рёбер. Это значит, что осталось провести ещё 8 игр. Получается, что ответ на вопрос задачи будет таким: проведено 7 игр, осталось провести 8 игр.
Отметим, что граф для одной и той же задачи можно нарисовать разными способами. И наоборот, для разных задач можно нарисовать одинаковые по виду графы.

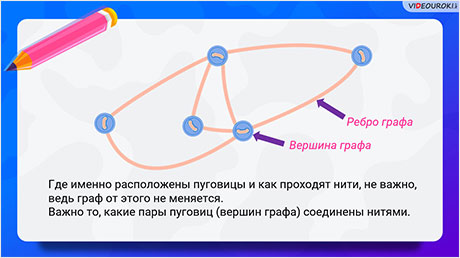
Граф можно представить как набор пуговиц, некоторые из которых соединены нитями. Пуговицы – это вершины графа, нити – его рёбра.

При этом, где именно расположены пуговицы, и как проходят нити не важно, ведь граф от этого не меняется. Важно то, какие пары пуговиц (то есть вершин графа) соединены нитями.
Но при решении задач, подобных приведённой, удобнее всё-таки располагать вершины по окружности. Тогда при проведении рёбер рисунок получается не таким запутанным.
Если из вершины графа выходит чётное количество рёбер, то её называют чётной. А если из вершины графа выходит нечётное количество рёбер, то её называют нечётной.
Посмотрите на такой граф.

У него вершины 1 и 4 являются нечётными, так как из них выходят по 3 ребра.
А вот вершины 2, 3 и 5 являются чётными, так как из вершины под номером 2 выходят 4 ребра, из вершины под номером 3 тоже выходят 4 ребра, а из вершины под номером 5 выходят 2 ребра.
На одном из наших занятий было предложено решить эту задачу с помощью таблицы. Давайте решим её с помощью рисунка.
Обозначим фамилии девочек буквами. Пусть напротив буквы Б будет белое платье, напротив буквы Ч – чёрное, напротив буквы К – красное.

Соединим пунктирной линией букву Б и белое платье. Это означает, что Белова не в белом платье. Также соединим пунктирными линиями букву Ч и чёрное платье, букву К и красное платье. Это означает, что Чернова не в чёрном платье, а Краснова не в красном платье.


Теперь, внимательно посмотрев на рисунок, становится понятно, что ни Белова, ни Чернова не одеты в белое платье. Значит, в белое платье одета Краснова. Поэтому соединим букву К и белое платье сплошной линией.

Так как на Чернова была одета не в белое платье, а также на ней не могло быть чёрного платья, то, следовательно, она была в красном платье. Соединим сплошной линией букву Ч и красное платье.

Мы выяснили, что Краснова была в белом платье, а Чернова была в красном. А значит, Белова была в чёрном платье. Соединим букву Б и чёрное платье сплошной линией.

Ответ на вопрос задачи будет таким: Белова была одета в чёрное платье, Чернова – в красное платье, Краснова – в белое платье.
И решим ещё одну задачу. Из города А в город Б ведут 3 дороги, а из города Б в город Б – 4 дороги. Сколькими способами можно проехать из города А в город В, если по пути надо обязательно заехать в город Б?
Решение. Отметим точками города А, Б и В. В условии задачи сказано, что из города А в город Б ведут 3 дороги. Также сказано, что из города Б в город В ведут 4 дороги.

Возьмём одну дорогу, которая ведёт из города А в город Б. Её можно продолжить до города В четырьмя различными способами.
Если взять вторую дорогу, которая ведёт из города А в город Б, то и её можно продолжить до города В четырьмя различными способами.
То же самое можно сказать и про третью дорогу, ведущую из города А в город Б, то есть её также можно продолжить до города В четырьмя способами.
Получается, что по какой бы из трёх дорог из города А в город Б мы не поехали, продолжить дорогу в город В можно четырьмя способами.
Таким образом, из города А в город В через город Б можно проехать 3 умножить на 4, то есть 12 способами.

Теория возникновения графа: Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783).Через город Кенигсберг протекает река Преголя. Она делится на два рукава и огибает остров. В XVIII веке в городе было семь мостов,
Рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз и вернуться к тому месту, откуда началась прогулка.
Многие горожане заинтересовались этой задачей, однако придумать решение никто не смог. Этот вопрос привлек внимание ученых разных стран.
Разрешить проблему удалось известному математику Леонарду Эйлеру.
Причем, он не только решил эту конкретную задачу, но придумал общий метод решения подобных задач. Эйлер поступил следующим образом: он "сжал" сушу в точки, а мосты "вытянул" в линии. В результате получилась фигура, состоящая из точек и линий, связывающих эти точки, которую называют графом.
Вершины, из которых выходит нечетное число ребер, называют нечетными вершинами, а вершины, из которых выходит четное количество ребер, - четными.
Решая задачу про Кенигсбергские мосты, Эйлер установил, в частности, следующие свойства графа:
1) Если в фигуре только четные вершины, то ее можно нарисовать одним росчерком, независимо от того, с какого места начинается черчение.
2) Если в фигуре имеется только одна пара нечетных вершин, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных вершин.
3) Если фигура имеет более одной пары нечетных вершин, то она вовсе не может быть нарисована одним росчерком.
4) Число нечетных вершин графа всегда четно.
5) Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа.
Например, если фигура имеет четыре нечетные вершины, то ее можно начертить самое меньшее двумя росчерками.В задаче о семи Кенигсбергских мостах все четыре вершины соответствующего графа - нечетные, т.е. нельзя пройти по всем мостам ровно один раз и закончить путь там, где он был начат.
Читайте также:

