Графики функций содержащих модули конспект урока 11 класс никольский
Обновлено: 07.07.2024
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Оборудование:
Тип урока: “Урок обобщения и систематизации знаний” (1V- тип).
Технология урока: Проектная деятельность, интегрированный урок (математика + информатика).
Результат урока нацелен на овладение учащимися программным и дополнительным материалом по данной теме и рассчитан на выход каждого ученика на свой уровень развития.
Построение графиков является основным рабочим материалом всего курса алгебры. Результат урока обоснован требованиями Программы к обязательной математической подготовке учащихся по данной теме:
освоить общие приемы построения графиков;
овладеть техникой построения графиков с помощью симметрии относительно осей координат;
научиться применять изученные приемы построения графиков в измененной ситуации для произвольных кривых.
Триединая дидактическая задача.
Образовательные задачи ставятся через конкретное содержание учебного материала и конкретную деятельность учащихся.
актуализация знаний о графиках функций и уравнений,
закрепление знаний о построении графиков линейной, квадратичной и тригонометрической функций,
повторение преобразования симметрии относительно прямой,
знакомство с графиком логарифмической функции,
укрепление умений и навыков в работе по образцу и в сходных условиях,
перенос знаний в новые условия.
развитие логического мышления, познавательного интереса, творческой активности,
развитие общеучебных навыков и умений – организационных, интеллектуальных и коммуникативных.
воспитание взаимопомощи, культуры общения, способствующей созданию благоприятного психологического климата, направленного на личностно-ориентированный подход к обучению и воспитанию.
Структура урока:
Этап всесторонней проверки знаний.
Этап усвоения новых знаний.
Этап закрепления нового.
Обобщение и систематизация знаний.
Применение знаний, умений и навыков в новых условиях.
Информация о домашнем задании.
Подведение итогов урока, рефлексия.
Для достижения триединой задачи использовались:
Методы обучения:
Формы организации познавательной деятельности:
Учитывая психолого-педагогическую характеристику класса и в соответствии с поставленными задачами, было отобрано следующее:
Содержание учебного материала:
- В домашнем задании были заложены все вопросы, которые помогут учащимся на уроке в ходе вопросно-ответной беседы самостоятельно овладеть новым материалом:
а) построении графиков функций и уравнений;
б) применение преобразования симметрии относительно прямой.
В ходе урока проводится:
а) повторение построения графиков линейной, квадратичной и тригонометрической функции;
б) формирование учебно-организационных и учебно-интеллектуальных навыков при выполнении практической работы;
в) формирование учебно-коммуникативных навыков в течение всего урока.
Для домашнего задания был отобран дифференцированный материал, охватывающий все опросы, рассмотренные на уроке.
Основная цель урока: С помощью вопросно-ответной беседы как одного из методов дидактической работы добиться того, чтобы учащиеся самостоятельно овладели новыми знаниями, с помощью наводящих вопросов учителя переносили усвоенные знания в новые условия, творчески применяли их. Для этого учебный материал урока должен быть подобран учителем продуманно и тщательно, с учетом прошлого опыта и ранее приобретенных знаний учащихся, с созданием проблемных ситуаций на уроке.
Ход урока
1. Орг. момент.
Приветствие, проверка присутствующих. Объяснение хода урока.
2. Этап всесторонней проверки знаний.
3. Этап усвоения новых знаний.
Урок построен в виде презентации мини-проектов. Учащиеся были предварительно разбиты на группы по два человека, которые изучали построение графиков функций и уравнений, содержащих переменную под знаком модуля в свете ранее изученных функций: 7 класс – линейная функция, 8 – 9 классы – квадратичная функция, 10 класс – тригонометрические функции, 11 класс – логарифмическая функция (самостоятельно). В ходе презентации один участник пары (теоретик) рассказывает о преобразованиях графиков, а другой (практик) показывает соответствующие преобразования на экране монитора.
I-я пара рассматривает линейную функцию y = x – 2

Задача 1. Построить график функции y = | x – 2 |

Задача 2. Построить график функции y = | x | – 2

Задача 3. Построить график уравнения | y | = x – 2

II-я пара рассматривает квадратичную функцию y = x 2 – 2х – 3.

Задача 1. Построить график функции y = | x 2 – 2х – 3 |

Задача 2. Построить график функции y = | x 2 | – 2 | х | - 3

Задача 3. Построить график уравнения | y | = x 2 – 2х - 3

III-я пара рассматривает тригонометрическую функцию y = sin х.

Задача 1. Построить график функции y = | sin х. |

Задача 2. Построить график функции y = sin | х |.

Задача 3. Построить график уравнения | y | = sin х

4. Подведение итогов (обобщение). Рассмотрим график произвольной функции y = f (х), заданной на промежутке [-8; 7].

IV-я пара. Задача 1. По известному графику функции y = | f (х) |. По определению имеем: | f (х) | =
Поэтому график функции y = | f (х) | совпадает с графиком функции y = f (х) на тех промежутках, где f (х) >=0, а на тех промежутках, где f (х)

Задача 2.
По известному графику функции y = f (х) построить график функции y = f ( | х | ). Если х >=0, то | х | = х, поэтому f ( | х | ) = f ( х ), т. е. при х >=0 графики функций y = f ( | х | ), и y = f (х) совпадают. Функция y = f ( | х | ) является четной, т. к. y = | х | - четная функция; поэтому её график при х =0.

Задача 3 По известному графику функции y = f (х) изобразить на плоскости множество точек, координаты которых удовлетворяют условию | y | = f ( х ).
Так как в левой части уравнения имеется знак модуля, то надо брать лишь те значения х, при которых f ( х ) >=0. Для этих значений равенство | y | = f ( х ) можно записать в виде у = +-f (х), т. е. мы имеем две функции. Если при всех значениях х выполняется неравенство f ( х )

5. Применение знаний, умений и навыков в новых условиях.
Задание классу (перенос знаний в новые условия).
Учитель: В 11-м классе мы будем изучать логарифмическую функцию.
Вам предлагается: график функции y=lnx

Попробуйте самостоятельно построить графики:
Ответы

6. Информация о домашнем задании.
Выполнить упражнения с карточки в тетради.
Для функций у = x-2.
Продумать построение графиков у = |f(|x|)| и |у| = |f(|x|)|.
Для функций у=х 2 -2x-3.
Продумать построение графиков у = |f(|x|)| и |у| = |f(|x|)|.
Для функций у = sin x.
Продумать построение графиков у = |f(|x|)| и |у| = |f(|x|)|.
7. Подведение итогов урока, рефлексия. Ученики и учитель подводят итоги урока, анализируют выполнение поставленных задач.

развивающие: развивать зрительную память, математически грамотную речь, аккуратность, точность в построении; умение анализировать, логическое мышление, память через использование образных подсказок.
воспитательные: создать условия для формирования ответственного отношения к учебному труду, развивать умения критически относиться к получаемой информации, аргументировать собственное высказывание.
Объект изучения: функции, содержащие переменную под знаком модуля
Предмет изучения: механизм построения графиков.
Модуль переменной (абсолютная величина значения) определяется следующим образом:
Чтобы ответить на этот вопрос, изучим алгоритм построения графика для функции y = |f (x)|, которая характерна тем, что не имеет отрицательных значений:
1) Построить график функции y = f(x).
2) Участок графика, расположенный ниже оси абсцисс (при отрицательных y) развернуть на верхнюю половину координатной сетки преобразованием симметрии относительно оси Ox, то есть отрицательные значения графика преобразуются в положительные.
Например, построим функцию y =|x|
1) Построим функцию y=x, то есть раскроем знак модуля согласно его определению y=x, х ≥ 0

2) Построим график функции y=-x, то есть раскроем знак модуля согласно его определению у=−x, х

3) Т. к. функция y = |f (x)| не имеет отрицательных значений, значит преобразуем отрицательные значения наших графиков в положительные, то есть все отрицательные значения по у сделаем положительными и получим:

Задача №1
(видеолекция)

Построить график функции y = | |
1. Построим функцию y= , то есть раскроем знак модуля согласно его определению y= , х ≥ 0
Для начала найдем вершину параболы:
= – координаты вершины параболы по оси х

- координаты вершины параболы по оси у
Затем узнаем в каких точках график пересекается с осью х:


D =
= =1
= =-5
Затем узнаем в каких точках график пересекается с осью y:

2) Т. к. функция y = |f (x)| не имеет отрицательных значений, значит преобразуем отрицательные значения наших графиков в положительные, то есть все отрицательные значения по у сделаем положительными и получим:

Построить график функции: 1) y=|x²+2x-3|
Построим функцию y = x²+2x-3, то есть раскроем знак модуля согласно его определению y=x²+2x-3, х ≥ 0
Для начала найдем вершину параболы:
= – координаты вершины параболы по оси х

- координаты вершины параболы по оси у
Затем узнаем в каких точках график пересекается с осью х:

D =
= =2
= =-3
Затем узнаем в каких точках график пересекается с осью y:
2) Т. к. функция y = |f (x)| не имеет отрицательных значений, значит преобразуем отрицательные значения наших графиков в положительные, то есть все отрицательные значения по у сделаем положительными и получим:
Построить график функции y = | |
Сначала построим график функции y= .
Затем преобразуем отрицательные значения наших графиков в положительные, то есть все отрицательные значения по у сделаем положительными и получим:
2) Алгебра. 9 класс: учеб. для общеобразоват. организаций/А45[Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]: под ред. С.А. Теляковского. – 4-е изд. – М.: Просвещение, 2017. – 287 с.

Цели урока:Обобщить и систематизировать знания учащихся по теме "Модуль", решению уравнений и неравенств с модулем.
Сформировать навыки построения графиков функций, содержащих знак модуля. Углубить знания учащихся по данной теме.Формировать познавательную активность учащихся, развивать исследовательсские способности.
Данное занятие следует за изучением методов решения уравнений и неравенств, содежащих модуль.
Ход урока. Урок начинается с проверки домашней работы, состоящей из решения уравнений, содержащих модуль. Классу предлагается рассказать о методах работы с уравнениями.Затем ребята слушают выступление ученика о решении более сложного уравнения.
Затем идет актуализация знаний по теме построение графиков функций с помощью преобразований.
С помощью презентации учащимся излагается методика построения графиков функций, содержащих модуль.
Выполняя группровую работу по построению графиков функций, содержащих модуль, учащиеся закрепляют полученные знания на практике. Подводится итог урока.
Урок алгебры в 9 классе.
Сформировать навыки построения графиков функций, содержащих знак абсолютной величины.
Организовать работу учащихся по указанным темам на уровне, соответствующем уровню уже сформированных знаний.
І этап урока - организационный (1 минута)
Учитель сообщает учащимся тему урока , цель и поясняет , что во время урока будет использоваться мультимедийное оборудование.
ІІ этап урока (7 минут)
С помощью фронтального опроса проверяется знание определения модуля. На доске, демонстрируется слайд из презентации, составленной учеником.
=
Термин модуль (от лат. modulus –мера) ввел английский математик Р.Котес (1682-1716), а знак модуля немецкий математик К. Вейерштрасс (1815-1897) в 1841 г.
Пользуясь определением можно решать уравнения и неравенства, содержащие модуль.
В качестве домашнего задания учащимся были заданы уравнения, содержащие модуль. Задача отвечающего охарактеризовать методы решения уравнений. Решение третьего уравнения заранее записано на доске одним из учащихся.





Проверь себя: 1). 6;-6; 2). 1; ; 3) 1; 4) -4; -0,5; 2; ;] [1;+).
III этап урока (10 минут)
Метод интервалов решения уравнений и неравенств, содержащих модуль.
Учащимся предлагается выслушать ученика, заранее подготовившего решение уравнения, задать ему вопросы по решению и записать решение.

Решить уравнение:
Ученик отвечает используя слайд презентации.
Выделим интервалы на каждом из которых выражения стоящие под знаком модуля сохраняют свой знак. Для этого найдем нули модулей: х+1=0; х=0; х-1=0; х-2=0 если х=-1; х=0; х=1; х=2.
Отметим найденные точки на координатной прямой:


(-;-1)

(2;+)
Учитывая знаки, раскроем модули:

Решение совокупности: -2; [2;+)
IV этап (12 минут)

Определение: Графиком функции модуль являются биссектрисы первого и второго координатных углов
Функция модуль является четной функцией
График функции модуль симметричен относительно оси ординат
Построение графиков вида:


К моменту работы с этой темой, учащиеся знакомы с графиком функции y=, с построением графиков с помощью преобразований. Эта часть урока систематизирует знания, и углубляет их. Учащиеся знакомятся с методикой построения графиков функций y=
Во многих случаях графики функций могут быть построены путем некоторых преобразований уже известных графиков других функций более простого вида. График функций вида:


может быть получен из графика функций при помощи следующих геометрических преобразований:
а) Осевой симметрии относительно оси абсцисс;
б) осевой симметрии относительно оси ординат;
в) центральной симметрии относительно начала координат;

а) Параллельного переноса (сдвига) вдоль оси абсцисс;
б) параллельного переноса (сдвига) вдоль оси ординат;
3. а) Растяжения (или сжатия) по направлению оси абсцисс;
б) растяжения (или сжатия) по направлению оси ординат;
а) При осевой симметрии относительно оси абсцисс точка переходит в точку ;
б) При осевой симметрии относительно оси ординат точка переходит в точку ;
в) При центральной симметрии относительно начала координат переходит в точку
3. а) При растяжении (сжатии) в k раз вдоль оси 0x относительно 0y точка переходит в точку.
б) При растяжении (сжатии) в q раз вдоль оси ординат относительно абсцисс точка переходит в точку .

Применительно к графикам функций эти свойства дают те конкретные геометрические преобразования (табл. 1), использование которых позволяет из известного графика функции строить графики других функций .
V этап урока (13 минут)
Класс делится на три команды, каждая команда получает задание:
1 команда. Построить графики: y=; .
2 команда. Построить графики: .
3 команда. Построить графики:
Построит графики функций, используя полученные знания. У каждой команды по 3 листа бумаги формата А3, на которых нарисована система координат. Ребята работают фломастерами, изображая графики. В работе принимают участие все члены каждой команды. По мере построения графиков, листы крепятся на доску магнитами.
После того как все графики готовы, к доске приглашаются ученики из каждой команды для проверки графиков соперников.
V этап урока (2 минуты)
Подведение итогов урока, домашнее задание.
Комментарии. Учитель комментирует выставленные на уроке оценки, подводит итог урока..

В презентации рассмотрены все возможные случаи построения графиков функций, содержащих модуль, показаны способы построения в зависимости от местоположения модуля или модулей в функции.
Описание разработки
По определению модуля, выражение y=|f(x)| равносильно системе

Подготовка к ГИА
Построение графиков функций, содержащих переменную под знаком модуля.
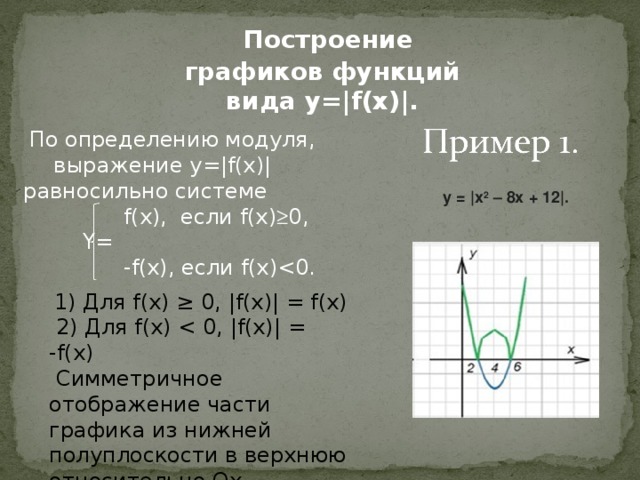
Построение графиков функций вида y=|f(x)|.
По определению модуля, выражение y=|f(x)| равносильно системе
y = |x 2 – 8x + 12|.
1) Для f(x) ≥ 0, |f(x)| = f(x)
Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox
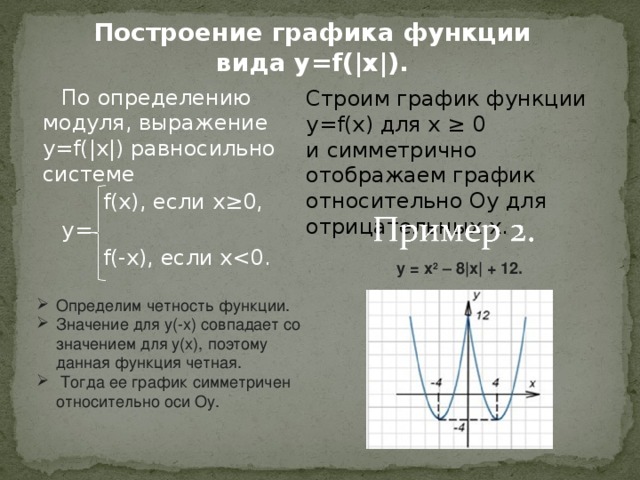
Построение графика функции вида y=f(|x|).
По определению модуля, выражение y=f(|x|) равносильно системе
Строим график функции y=f(x) для x ≥ 0
и симметрично отображаем график относительно Oy для отрицательных x.
y = x 2 – 8|x| + 12.
Построение графика функции вида Y=|f(X)|+|G(x)|.
- Для построения графика функций такого вида нужно найти нули каждой функции под знаком модуля и нанести их на координатную прямую.
- На каждом из полученных промежутков необходимо раскрыть модули по определению, т.е. в зависимости от знака функции под модулем на данном промежутке.
- Затем нужно построить каждую из полученных функций у на их области определения; полученный график - искомый.
y = |x + 1| – |x – 2|.
y = 2x – 1, при -1 ≤ x
-3, при x
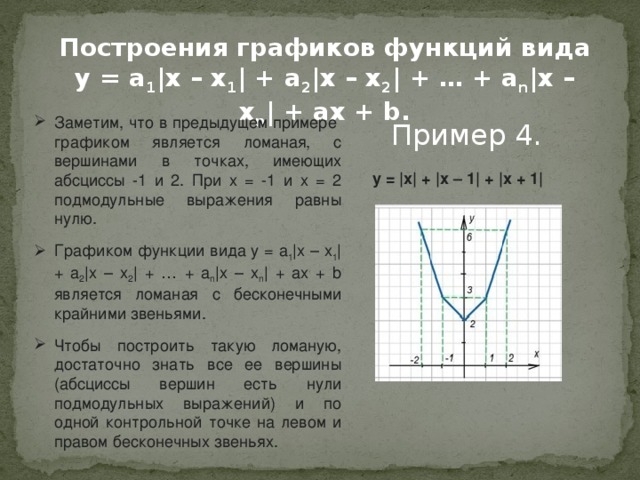
Построения графиков функций вида
y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b.
- Заметим, что в предыдущем примере графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю.
- Графиком функции вида y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b является ломаная с бесконечными крайними звеньями.
- Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
y = |x| + |x – 1| + |x + 1|
Для построения графика такой функции необходимо:
- сначала построить график функции внутреннего модуля(у=|f(x)|)
- потом преобразовать его в график у=||f(x)|+a|
- затем - в график у=|||f(x)|+a|+b|
т.е. последовательно раскрывать модули, начиная с внутреннего.
Запишем цепочку последовательных преобразований:
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.

1; его растяжением в 1/а раз к оси у, если 1симметрией относительно оси х, если а" width="640"
Построение графика функции вида y=g(х)|f(x)|.
Если g(X)=a , то у=а|f(x)|. Тогда график функции у=а|f(x)| можно получить из графика функции у=|f(x)|
Построение графика функции вида y=g(х)|f(x)|.
Если g(x) a , то
- находим нули функции под модулем и наносим их на координатную прямую.
- раскрываем модуль на получившихся промежутках по определению и перемножаем функции.
Нуль функции f(x)=|х| х=0 делит координатную прямую на два промежутка - (- ;0) и[0;+ ); на каждом из них раскроем модуль:
х 2 +2x, если х 0,

-(х 2 +2х), если х
Построение графика функции вида |y|=f(x).
По определению модуля, выражение |у|=f(x) равносильно системе
Значит, чтобы построить график функции |у|=f(x), необходимо сначала построить график функции у=f(x), его часть, расположенную выше оси Х, оставить без изменений и , отбросив часть, расположенную ниже оси Х, отобразить симметрично относительно оси Х.
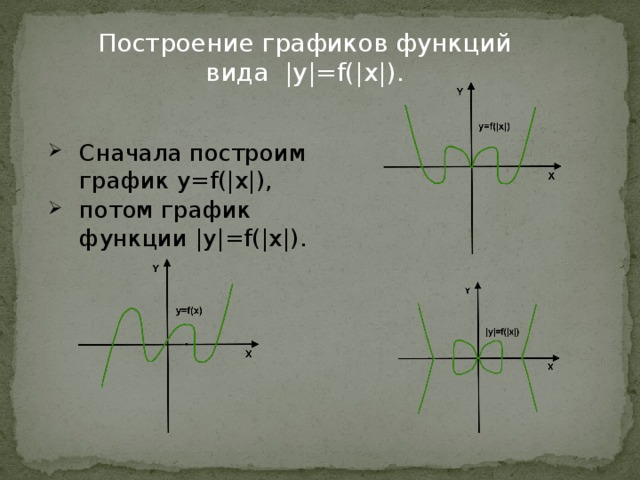
Построение графиков функций вида |y|=f(|x|).
Построение графиков функций вида |y|=|f(x)|.
- сначала построим график y=|f(x)|
- потом |y|=|f(x)|

-75%
Читайте также:

