Формулы сложения конспект урока
Обновлено: 22.07.2024
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
1. Число :
2. Тема урока : Формулы сложения
3. Тип урока : урок ознакомления с новым материалом
4. Цель урока : сформировать умение применять тригонометрические формулы сложения
5. Учебно-воспитательные задачи урока:
Образовательные:
· вывод формул сложения для тригонометрических функций
· отработать навыки использования тригонометрических формул сложения при решении уравнений, в вычислениях и тождественных преобразованиях тригонометрических выражений
Развивающие
· Развитие умений выделять главное, существенное в изученном материале
· Развивать познавательный интерес, логическое мышление
Воспитательные
· воспитание интереса к предмету
· воспитание ответственного отношения к своему образованию.
7. План урока
Этапы урока
Методы и методические приемы
Изложение нового материала
Подведение итогов. Домашнее задание. Рефлексия
Словесный (запись на доске), оценивание
8. Ход урока
I. Организационный момент. Приветствие учителя. Проверка готовности класса к уроку.
II I . Объяснение нового материала.
Определение: Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.
Формулы сложения - это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенса суммы и разности аргументов.
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)
Рисунок 1 . Единичная окружность
Точка получена поворотом точки Мₒ(1;0) на угол , а точка на угол и точка на угол .
Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты
;
;
).
Подставим координаты точек и в формулу для нахождения расстояния между ними. Получим:
Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:
Преобразуем правую часть:
Соединим левую и правую части:
Разделим на каждое слагаемое :
Получили формулу косинуса суммы.
Заменим и учтём, что , получим формулу косинуса разности
Докажем, что
Так как , , то по формуле косинуса разности получаем:
Заменим получим
Так, например, , потому что .
Докажем, что
Подставим в формулу значение , получим:
Для тангенса и котангенса тоже справедливы формулы
Выведем формулу синуса суммы и разности:
Для тангенса тоже есть формула суммы и разности. По определению .
Получаем формулу тангенса суммы .
Заменим в ней и учтём, что tg 〖 (-α)= 〖 -tg 〗 α 〗 , получим формулу тангенса разности
.
Пример. Вычислим .
Для котангенса суммы и разности применяют формулы:
Физкультминутка.
IV . Закрепление материала
Пример 1. Найти
Решение: Представим , так как нам известны значения косинуса углов и Подставим в формулу косинуса суммы. Получаем:
Ответ: .
Пример 2. Найти .
Решение: Представим , так как нам известны значения синуса углов и Подставим в формулу синуса суммы. Получаем:
Ответ: .
Ответ: .
Выполнение заданий из учебника: №№ 481,482 (1,3), 483 (1), 484 (1,3), 485 (1,3)
V . Итоги урока. Рефлексия
Домашнее задание. П.28 . №№ 482 (2,4), 483 (2), 484 (2,4), 485 (2,4).
Формулы сложения - это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенс суммы и разности аргументов.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)

Рисунок 1 – единичная окружность
Точка получена поворотом точки Мₒ(1;0) на угол , а точка на угол и точка на угол .
Углы и равны, отрезки . Значит, треугольник равен треугольнику , следовательно у них одинаковые стороны и .
Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты

;

).
Подставим координаты точек и в формулу для нахождения расстояния между ними. Получим:

Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:

Преобразуем правую часть:

Соединим левую и правую части:

Разделим на каждое слагаемое :

Получили формулу косинуса суммы.
Заменим и учтём, что , получим формулу косинуса разности


Докажем, что
Так как , , то по формуле косинуса разности получаем:

Заменим получим

Так, например,, потому что .

Докажем, что
Подставим в формулу значение , получим:
Для тангенса и котангенса тоже справедливы формулы


Выведем формулу синуса суммы и разности:


В этой формуле заменим и получим формулу синуса разности:


Для тангенса тоже есть формула суммы и разности. По определению .

Тогда tg , разделим числитель и знаменатель на


Получаем формулу тангенса суммы .

Заменим в ней и учтём, что tg〖(-α)=〖-tg〗α 〗, получим формулу тангенса разности

.

Пример. Вычислим .
Для котангенса суммы и разности применяют формулы:

Примеры и разбор решения заданий тренировочного модуля
Решение: Представим , так как нам известны значения косинуса углов и Подставим в формулу косинуса суммы. Получаем:

Пример 2. Найти .
Решение: Представим , так как нам известны значения синуса углов и Подставим в формулу синуса суммы. Получаем:

Ответ: .

Пример 3. Вычислите .

Решение: Применяем формулу синуса разности: .

Ответ: .

воспитание ответственного отношения к своему образованию.
Этапы урока
Методы и методические приемы
Изложение нового материала
Подведение итогов. Домашнее задание. Рефлексия
Словесный (запись на доске), оценивание
8. Ход урока
I. Организационный момент. Приветствие учителя. Проверка готовности класса к уроку.
III. Объяснение нового материала.
Определение: Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.
Формулы сложения - это формулы синуса суммы и разности аргументов; косинуса суммы и разности аргументов; тангенса суммы и разности аргументов.
Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)

Рисунок 1. Единичная окружность
Точка получена поворотом точки Мₒ(1;0) на угол , а точка на угол и точка на угол .
Углы и равны, отрезки . Значит, треугольник равен треугольнику , следовательно у них одинаковые стороны и .
Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты

;

;

).
Подставим координаты точек и в формулу для нахождения расстояния между ними. Получим:


.
Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:

Преобразуем правую часть:

Соединим левую и правую части:


Разделим на каждое слагаемое :
Получили формулу косинуса суммы.
Заменим и учтём, что , получим формулу косинуса разности
Так как , , то по формуле косинуса разности получаем:
Так, например, , потому что .
Подставим в формулу значение , получим:
Для тангенса и котангенса тоже справедливы формулы
Выведем формулу синуса суммы и разности:
В этой формуле заменим и получим формулу синуса разности:
Для тангенса тоже есть формула суммы и разности. По определению .
Тогда tg , разделим числитель и знаменатель на
Получаем формулу тангенса суммы .
Заменим в ней и учтём, что tg〖(-α)=〖-tg〗α 〗, получим формулу тангенса разности
Для котангенса суммы и разности применяют формулы:
Физкультминутка.
IV. Закрепление материала
Решение: Представим , так как нам известны значения косинуса углов и Подставим в формулу косинуса суммы. Получаем:
Решение: Представим , так как нам известны значения синуса углов и Подставим в формулу синуса суммы. Получаем:
Пример 3. Вычислите .
Решение: Применяем формулу синуса разности: .
Выполнение заданий из учебника: №№ 481,482 (1,3), 483 (1), 484 (1,3), 485 (1,3)
V. Итоги урока. Рефлексия
Домашнее задание. П.28 . №№ 482 (2,4), 483 (2), 484 (2,4), 485 (2,4).

В данном видеоуроке мы познакомимся a формулами сложения для синуса и косинуса, а также для тангенса. Научимся применять эти формулы на практике.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Формулы сложения"
Прежде, чем приступить к рассмотрению новой темы, вспомним, что квадрат расстояния между точкой и точкой выражается следующей формулой: . Вспомним основное тригонометрическое тождество: , а также формулы, выражающие зависимость между синусами, косинусами, тангенсами и котангенсами противоположных углов: , , .
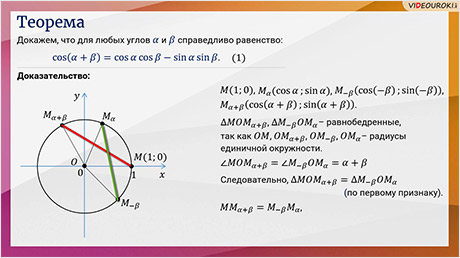
Теперь мы с вами познакомимся с формулами сложения. Давайте докажем, что для любых углов и справедливо равенство: .
Доказательство. Пусть на координатной плоскости изображена единичная окружность с центром в начале координат. Точка совершает поворот на угол и оказывается в точке . Затем точка совершает поворот на угол и оказывается в точке . И совершает поворот на угол и оказывается в точке .
. По определению синуса и косинуса: ), ,.
Давайте рассмотрим треугольники и . Эти треугольники равнобедренные, так как две стороны каждого из них являются радиусами нашей единичной окружности. При этом . Следовательно, рассматриваемые треугольники равны по двум сторонам и углу между ними, то есть по первому признаку равенства треугольников. А значит, основания этих равнобедренных треугольников равны, то . Квадраты этих оснований также равны: .
Преобразуем это выражение. В первую очередь воспользуемся известными нам формулами и запишем в правой части , а : . Теперь воспользуемся формулой квадрата разности и выполним возведение в квадрат в левой части, воспользуемся формулами квадрата разности и квадрата суммы и выполним возведение в квадрат в правой части:
По основному тригонометрическому тождеству в левой части сумма первого и последнего слагаемых равна , в правой части и равна , а также сумма и равна : . Теперь выполним несложные преобразования: , . И в результате получим, что . Что и требовалось доказать.
Теперь в доказанной формуле заменим на : [воспользуемся известными нам формулами , ] . Таким образом, получили .
Мы познакомились с формулами сложения для косинуса. А для синуса есть такие формулы? Прежде чем познакомиться с формулами сложения для синуса, давайте докажем следующие формулы: и . Для этого в формулу вместо подставим : . Таким образом, . Если мы заменим в этой формуле на , то получим формулу .
А если мы в формулу вместо подставим : . Выполним преобразования: , . И поменяем местами правую и левую части, то получим формулу .
Далее, применяя все полученные выше формулы, мы с вами выведем формулы сложения для синуса. Итак, применив формулу справа налево, запишем [перепишем выражение под знаком косинуса] [применим формулу ] [по формуле вместо к запишем , по формуле вместо запишем ] . Таким образом, мы получили, что .
Теперь в формуле заменим на : [в правой части запишем как , запишем как ] . Получаем: .
Таким образом, мы познакомились с формулами, которые называют формулами сложения.
Давайте вычислим , .
[применим формулу ] [подставим значения синусов и косинусов] .
[применим формулу ] [теперь подставим значения синуса и косинуса] .
Сейчас, прежде чем приступить к практической части нашего урока, давайте докажем следующее равенство: . Для этого запишем левую часть этого равенства как [преобразуем числитель по формуле , а знаменатель преобразуем по формуле ] [теперь разделим числитель и знаменатель дроби на произведение . При этом отметим, что , так как делить на нуль нельзя] . Равенство доказано.
. [применим формулу ] .
Подставим значения и :
Читайте также:

