Физический смысл производной конспект

Обновлено: 05.07.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №10. Определение производной. Физический смысл производной.

Перечень вопросов, рассматриваемых в теме

1) Определение производной;

2) Физический смысл производной;

2) Приращение функции;

3) Скорость материальной точки в заданный момент времени по данному закону движения.

Глоссарий по теме

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.

Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

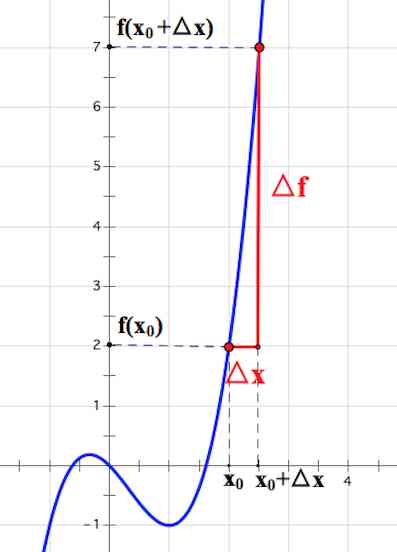
Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.

Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.

Нельзя истолковывать термин "приращение" как "прирост".

Примеры и разбор решения заданий тренировочного модуля

Найдем приращение Δx и Δf в точке x_0, если f(x)= x 2 , x₀=2 и х=1,9

Δf= f(1,9) –f(2)=1,9 2 -2 2 =-0,39

Ответ: Δx=-0,1; Δf =-0,39

Найдем приращение Δx и Δf в точке x_0, если f(x)= x 2 , x₀=2 и х=2,1

Δf= f(1,9) –f(2)=2,1 2 -2 2 =0,41

Ответ: Δx=0,1; Δf =0,41

Найдем приращение Δf функции в точке x₀,если приращение аргумента равно x₀.

по формуле (1) находим:

С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t₀; t₀+∆t]. Если точка движется по прямой и известна ее координата x(t), то

Эта формула верна и для ∆t

Аналогично выражение называют средней скорость изменения функции на промежутке с концами х₀ и х₀+∆х.

Обозначение: y’ или f’(x)

Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.

Схема вычисления производной функции

Разделить приращение функции на приращение аргумента:

Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Вычислить производную функции y=x 2

Решение: Используем схему вычисления производной по действиям:

Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).

Таким образом, скорость – есть производная от пути по времени.

Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.

Необходимое и достаточное условие дифференцируемости

Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x₀, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.

Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.

Тип урока: Урок освоения новых знаний.

Формы работы: фронтальная, индивидуальная, групповая.

Содержание урока: §5 учебника пункт 21, стр. 137-142.

Оборудование: Компьютер, интерактивная доска, презентация, учебник.

Структура урока:

Организационный момент, постановка цели урока
Изучение нового материала
Первичное закрепление нового материала
Самостоятельная работа
Итог урока. Рефлексия.

Ход урока

I. Организационный момент, постановка цели урока (2 мин.)

II. Изучение нового материала (10 мин.)

Учитель: На предыдущих уроках мы познакомились с правилами вычисления производных, научились находить производные линейной, степенной, тригонометрических функций. Узнали, в чем заключается геометрический смысл производной. Сегодня на уроке мы узнаем, где в физике применяется данное понятие.

Для этого вспомним определение производной (Слайд 2)

Теперь обратимся к курсу физики (Слайд 3)

Учащиеся рассуждают, вспоминают физические понятия и формулы.

Пусть тело движется по закону S(t)= f(t) Рассмотрим путь, пройденный телом за время от t₀ до t₀+ Δ t, где Δt – приращение аргумента. В момент времени t₀ телом пройден путь S(t₀), в момент t₀+Δt – путь S(t₀ +Δt). Поэтому за время Δt тело прошло путь S(t₀+Δt) –S(t₀), т.е. мы получили приращение функции. Средняя скорость движения тела за этот промежуток времени υ==

Чем меньше промежуток времени t, тем точнее мы можем узнать, с какой скоростью движется тело в момент t. Устремив t →0, получим мгновенную скорость – числовое значение скорости в момент t этого движения.

υ= , при Δt→0 скорость – есть производная от пути по времени.

Слайд 4

Вспомним определение ускорения.

Применяя изложенный выше материал можно сделать вывод, что при t а(t)= υ’(t) ускорение – есть производная от скорости.

Далее на интерактивной доске появляются формулы силы тока, угловой скорости, ЭДС и т.д. Учащиеся дописывают мгновенные значения данных физических величин через понятие производной. (При отсутствии интерактивной доски использовать презентацию)

Вывод формулируют учащиеся.

Вывод: (Слайд 9) Производная – это есть скорость изменения функции. (Функции пути, координаты, скорости, магнитного потока и т.д.)

Учитель: Мы видим, что связь между количественными характеристиками самых различных процессов исследуемых физикой, техническими науками, химией, аналогична связи между путем и скоростью. Можно привести множество задач, для решения которых также необходимо находить скорость изменения некоторой функции, например: нахождение концентрации раствора в определенный момент, нахождение расхода жидкости, угловой скорости вращения тела, линейной плотности в точке и т.д. Некоторые из таких задач мы сейчас решим.

III. Закрепление полученных знаний (работа в группах) (15 мин.)

С последующим разбором у доски

Перед решением задач уточнить единицы измерения физических величин.

Задание 1 группе

Точка движется по закону s(t)=2t³-3t (s – путь в метрах, t – время в секундах). Вычислите скорость движения точки, ее ускорение в момент времени 2с

Задание 2 группе

Маховик вращается вокруг оси по закону φ(t)= t 4 -5t. Найдите его угловую скорость ω в момент времени 2с (φ – угол вращения в радианах, ω – угловая скорость рад/с)

Дано:	Решение:
φ(t)=t 4 -5t t=2с ______________ φ(2)=?	ω(t)= φ’(t) ω(t)=(t 4 -5t)’= 4t³-5 ω(2)=4·2³-5=32-5=27рад/c Ответ: ω(2)= 27рад/c

Задание 3 группе

Тело массой 2 кг движется прямолинейно по закону х(t)=2-3t+2t²

Найдите скорость тела и его кинетическую энергию через 3с после начала движения. Какая сила действует на тело в этот момент времени? (t измеряется в секундах, х – в метрах)

Задание 4

Точка совершает колебательные движения по закону х(t)=2sin3t. Докажите, что ускорение пропорционально координате х.

Дано:	Решение:
х (t)= 2sin3t ______________ а(t)	a(t)=υ’(t)=х’’(t); υ(t)=х’(t); υ(t)=(2sin3t)’=6cos3t a(t)=(6cos3t)’=-18 sin3t=-9·х(t) Ответ: a(t)=-9·х(t)

IV. Самостоятельное решение задач №272, 274, 275, 277

Производной функции в точке называется предел отношения приращения функции к приращению аргумента при , если этот предел существует.

Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…

Геометрический смысл производной

Если мы рассмотрим прямоугольный треугольник , то заметим, что есть .

Производная в точке равна тангенсу угла наклона касательной к графику функции в этой точке:

где – угол наклона касательной (проведенной к в т. )

Физический смысл производной

Если точка движется вдоль оси и ее координаты изменяются по закону , то мгновенная скорость точки :

Пример. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .

 Повторить основные формулы и правила дифференцирования.

 Рассмотреть на примерах решения практических задач, как применяется производная в химии, физике, биологии, экономике.

Тема урока:
Физический смысл производной в решении задач

Повторить основные формулы и правила дифференцирования.

Рассмотреть на примерах решения практических задач, как применяется производная в химии, физике, биологии, экономике.

Прежде чем вспомнит какую тему этого урока мы определили на предыдущем занятии, я предлагаю вам выполнить тестовое задание. Вам необходимо в течении 3-х минут определить ключевое слово сегодняшнего урока. Выполнив задание. запишите получившееся слово в таблицу. Желаю вам успеха. (ученики работают над расшифровкой слова)

Найдите производную функции:

у = х - 4

у = х -

у = х 5 + 3х 4 -2х – 5

И 1 +

3 2x 2

Ф 12x 2

С 1 -

Я 5х 4 +12х 3 – 2

К -

Л x 3

М 4x 3

-Какое слово у вас получилось? (флюксия) В течении урока вы работаете с листом самооценивания, не забывая оценивать себя после каждого этапа урока.

- Что это означает?

Исаак Ньютон (1642-1727) один из создателей дифференциального исчисления.

Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её физический и механический смысл.

Интересно: Исаак Ньютон называл производную флюксией, а саму функцию - флюентой.

Итак, сегодня на уроке мы будем говорить о производной, и не только.

Предлагаю вам решить задачу:

Мама с своей дочкой гуляла в парке. Девочка захотела покататься на каруселях, а мама решила сфотографировать дочку. Вращение карусели совершается по закону φ(t)=1/9t³-2/5t². Фотография может быть хорошего качества только при ускорении равном 3 м/с². В какой момент времени необходимо сделать снимок?

Проанализируем условие задачи и вопрос .(известен закон движения карусели и задано ускорение)

Какие величины характеризуют условие задачи? (физические величины: скорость, время, ускорение)

Какое свойство производной функции может нам помочь выявить закономерности между этими величинами и поможет решить задачу? (Физический смысл производной).

Запишем тему урока в тетради " Физический смысл производной в решении задач".

Вспомним физический смысл производной.

Если известен закон движения

материальной точки (тела)

x(t), s(t) или φ(t), то мгновенная

скорость в момент времени t

вычисляется по формуле

а ускорение a(t) = v׳(t)= x׳׳(t).

Прежде чем мы продолжим решение предложенной вам задачи, обратимся к таблице №1 в которой представлены задачи из открытого банка ЕГЭ, в решении которых используется физический смысл производной. Вспомним этапы решения этих задач проговаривая и фиксируя в правом столбце таблицы пошаговый алгоритм решения каждой задачи.

Попробуем составить таблицу-алгоритм решения вместе (проговариваем вместе, решение задачи на доске сравниваем с эталоном на экране, исправляем неточности и ошибки).

№1. При движении тела по прямой расстояние S(км) от начальной точки меняется по закону S(t) = 8t +t³ . Найдите формулу для вычисления скорости в любой момент времени и вычислите её при t= 2 с.

Определим, по какому закону изменяется скорость тела, применяя физический смысл производной

v(t) = S ׳(t)

По условию задачи, время равно 2 секунды, Вычисляя значение полученного выражения при t= 2 с. отвечаем на поставленный вопрос.

№2. Материальная точка движется прямолинейно по закону x(t) = 1/6t² + 5t + 28 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения).

В какой момент времени её скорость будет равна 6 м/с?

Определим, по какому закону изменяется скорость тела, применяя физический смысл производной

По условию задачи, скорость равна 6 м/с. Тогда полученное выражение приравниваем к 6, т.е. получаем уравнения, при решении которого отвечаем на поставленный вопрос.

№3. Материальная точка движется прямолинейно по закону S(t) = t³ -3/2t² + 2t - 1 (где S — расстояние от точки отсчета в метрах, t — время в секундах, измеряемое с начала движения).

В какой момент времени её ускорение будет равно 9 м/с²?

Определим, по какому закону изменяется скорость тела, применяя физический смысл производной:

v(t) = S ׳(t)=3t²-3t +2

Определим, по какому закону изменяется ускорение данного тела, применяя механический смысл производной:

По условию задачи, ускорение равно 9 м/с² , тогда полученное выражение приравниваем к 9, т.е. получаем уравнения, при решении которого отвечаем на поставленный вопрос.

_{Проверим решение задач на слайде.}

А теперь вернёмся к предложенной ранее задаче и сравним её условие с условиями уже решённых задач. По какому из алгоритмов можно решить эту задачу?

Решают самостоятельно ( проверяем со слайда)

v(t) = φ ׳(t)=1/3t²-5t

a(t)=v´(t) = 2/3t -5

2/3t -5= 3

Ответ: фотографировать девочку необходимо на 12 секунде.

Итак, мы решили задачу связанную с реальной жизненной ситуацией.

Рассмотрим ещё несколько примеров применения производной в процессах и явлениях реального мира.

Читайте также: