Центр тяжести конспект по технической механике

Обновлено: 05.07.2024

Момент силы зависит от ее плеча, а значит, и от точки приложения силы. Когда на тело действуют силы со стороны тросов, пружин и т. п., то положение точек приложения сил очевидно. Но что можно сказать о точке приложения силы тяжести?

Особенностью силы тяжести является то, что она действует на тело не в одной какой-то точке, а по всему объему тела. Силы тяжести, действующие на отдельные элементы тела, направлены к центру Земли и, следовательно, строго говоря, не будут параллельными. Однако размеры всех сооружений на Земле значительно меньше ее радиуса. Поэтому практически все эти силы можно считать параллельными.

Точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела (при любом положении тела в пространстве), называется центром тяжести.

Определение центра тяжести тела простой формы

Найдем вначале положение центра тяжести для наиболее простого случая, когда тело состоит из двух шаров различных масс, соединенных стержнем, массой которого можно пренебречь по сравнению с массами шаров. Кроме того, длину стержня будем считать значительно превышающей радиусы шаров. Тогда шары можно считать материальными точками (рис. 8.4, а).

Итак, на материальные точки А и Б, соединенные невесомым стержнем, действуют силы тяжести ₁ и ₂, параллельные друг другу. Геометрическая сумма этих сил представляет собой результирующую силу тяжести:

Она направлена к центру Земли, так же как и силы ₁ и ₂, а ее модуль равен сумме модулей слагаемых сил.

Положение центра тяжести, т. е. точки приложения результирующей силы, можно определить, используя тот простой факт, что тело, закрепленное на оси, проходящей через центр тяжести С, должно находиться в равновесии. Ведь относительно этой оси моменты сил тяжести _т и силы реакции опоры равны нулю, так как равны нулю плечи этих сил (рис. 8.4, б).

С другой стороны, согласно условию равновесия (8.2.5), можно записать: F₁d₁ - F₂d₂ = 0, где d₁ = АС и d₂ = СВ — плечи сил ₁ и ₂. Отсюда

Равенство (8.3.2) определяет положение центра тяжести рассматриваемого тела. Точка приложения равнодействующей параллельных сил тяжести делит расстояние между точками приложения этих сил на отрезки, обратно пропорциональные модулям сил.

Нахождение центров тяжести тел является важной технической задачей, так как от положения центров тяжести зависит устойчивость мостов, плотин, зданий, телевизионных вышек, автомашин, ракет на старте и т. п. Нужно поэтому познакомиться с методами нахождения центров тяжести тел различной формы.

Нахождение центра тяжести тел

В технике и повседневной жизни мы встречаемся с телами самой различной формы. Часто они состоят из стержней и дисков (колесо на оси, спортивная штанга и т. д.). Многие плоские фигуры состоят из прямоугольных и треугольных пластин. При определении положения центра тяжести подобных тел проще всего вначале определить положение центров тяжести отдельных его частей простой формы. У тел простой формы можно сразу указать положение центра тяжести, руководствуясь соображениями симметрии.

Так, центр тяжести однородного стержня, очевидно, располагается в середине стержня (рис. 8.5). У всех однородных фигур, имеющих центр симметрии, центр тяжести совпадает с этим центром: у круга — с его геометрическим центром, у параллелограмма — с точкой пересечения диагоналей и т. д. При этом центр тяжести может находиться и вне тела (например, у кольца или пустотелой сферы).

Определив положения центров тяжести составных частей тела сложной формы, можно найти, где расположен центр тяжести всего тела. Для этого надо заменить тело системой материальных точек, каждая из которых помещается в центре тяжеети соответствующей части тела и имеет массу этой части (рис. 8.6).

Координаты центра тяжести твердого тела

Рассмотрим теперь общий метод определения координат центра тяжести произвольного твердого тела. Для решения задачи предположим, что равнодействующая сил тяжести, приложенных к отдельным элементам тела, и точка ее приложения уже найдены.

Пусть сила тяжести равна _т и приложена в точке С (рис. 8.7) с координатами х, y, z. Приложим теперь к телу в другой точке внешнюю силу такую, чтобы тело находилось в равновесии. Это можно сделать, например, подвесив тело в точке D на нити или закрепив в этой точке другим способом. Так как в этом случае можно считать, что на тело действуют только две силы и _т, то согласно условию равновесия (8.2.1):

Отсюда следует, что сила должна быть равна по модулю и противоположна по направлению силе _т.

Разобьем теперь мысленно тело на элементы (материальные точки) и запишем условие равновесия, уже не заменяя равнодействующей совокупность элементарных сил тяжести:

(здесь Δ_т1 = Δm₁ — сила тяжести, действующая на произвольный малый элемент массой Δm₁).

Из (8.3.3) и (8.3.4) следует, что

(здесь m = — масса тела).

Таким образом, равнодействующая направлена вниз и равна сумме всех элементарных сил тяжести.

Вспомним теперь, что рассматриваемое тело находится в покое. Это значит, что совокупное действие силы и силы _т, заменяющей многочисленные элементарные силы тяжести, не вызывает вращения тела. Следовательно, выполняется условие равновесия (8.2.4) для моментов всех сил относительно любой неподвижной оси. В качестве таковой удобно взять одну из координатных осей, например ось OZ (рис. 8.8). Момент М равнодействующей _т и момент М' силы должны в сумме давать при равновесии нуль:

Очевидно, что условие (8.3.5) сводится к требованию, чтобы равные по модулю и противоположные по направлению силы и _т имели бы одну и ту же линию действия.

В то же время если не заменять элементарные силы тяжести равнодействующей, то условие равновесия (8.3.5) для моментов должно выполняться в виде

Из уравнений (8.3.5) и (8.3.6) следует, что

т. е. момент равнодействующей относительно какой-нибудь неподвижной оси равен сумме моментов всех элементарных сил тяжести относительно той же оси.

Подсчитаем упомянутые моменты сил относительно оси OZ. Как известно, момент силы равен произведению силы на плечо. Для силы Δ_тi плечом является координата x_i элемента малой массы Δmi (см. рис. 8.8). Поэтому момент силы Δ_тi равен: Δ_тix_i = Δm_ix_ig, а общий момент всех сил тяжести равен:

Мы предположили, что точка, в которой приложена суммарная сила _т, имеет координату х. Тогда суммарная сила создает момент относительно той же оси OZ, равный

Поскольку этот момент должен быть равен моменту, определяемому по формуле (8.3.7), то

Отсюда для координаты точки приложения равнодействующей всех параллельных сил тяжести получаем:

Мы нашли только одну из координат точки приложения равнодействующей. Другие координаты остались неопределенными, что и понятно, поскольку найденную точку можно переносить, например, вверх или вниз без изменения момента сил относительно оси OZ.

Однако этот способ можно применить еще раз, повернув оси координат вместе с телом так, чтобы вверх теперь была направлена уже другая ось (рис. 8.9).

Найдем вторую координату точки приложения суммарной силы:

а затем и третью:

Координаты центра тяжести, следовательно, определяются по формулам (8.3.8), (8.3.9), (8.3.10). Если использовать векторную форму записи, то все эти три формулы будут эквивалентны одной:

Центр тяжести и центр масс

Нетрудно заметить, что формула (8.3.11) совпадает с выражениями (7.3.4), которые определяют положение центра масс тела. Таким образом, в случае, когда размеры тела малы по сравнению с расстоянием до центра земного шара, центр тяжести совпадает с центром масс тела.

Кроме того, очевидно, что высказанные положения применимы и к расчету положения точки приложения силы инерции при поступательном движении. В самом деле, для такого расчета мы можем аналогичным образом разбить тело на малые элементы, к каждому из которых будет приложена сила инерции - Δm_i , где — ускорение системы отсчета. Как и при нахождении центра тяжести, все силы инерции параллельны и пропорциональны массам отдельных элементов. Поэтому сила инерции в неинер-циальной системе отсчета, движущейся поступательно, приложена всегда к центру масс (центру тяжести) тела. Наоборот, центробежная сила инерции в общем случае не приложена к центру масс, так как из-за различных расстояний до оси вращения на элементы даже одинаковой массы действуют в неинерци-альной системе отсчета различные центробежные силы инерции.

Мы получили более полное представление о центре тяжести. Практически во всех встречающихся задачах центр тяжести тела совпадает с его центром масс.

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).

Радиус-вектор этой точки

Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.

Если удельный вес однородного тела γ, вес элементарной частицы тела

подставить в формулу для определения r_C, имеем

Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)

Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

- Рамки A4 для учебных работ
- Миллиметровки разного цвета
- Шрифты чертежные ГОСТ
- Листы в клетку и в линейку

Точку, в которой действующие силы на физический объект уравнивают друг друга, называют центром тяжести тела. В геометрии этот термин совпадает с понятием центр масс. Зная его месторасположение, инженеры создают машины и различные механизмы, находящиеся в равновесии. Изменение же его положения позволяет осуществлять нужное перемещение путём падения тела, поэтому расчёт координат места равновесия так важен для практического применения.

Общие сведения

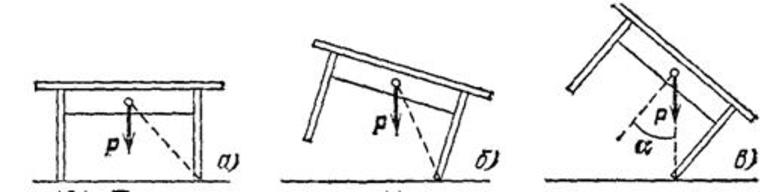
Пусть имеется физическое тело, на которое не оказывается влияние, то есть другие объекты не действуют или их силы воздействия скомпенсированы. Рассматриваемое тело будет находиться в состоянии прямолинейного движения или покоя. Для удобства можно принять, что объект неподвижен, например, пусть это будет лодка на поверхности воды.

Если к плавательному средству приложить силу, смещённую к началу лодки F1, судно начнёт поворачиваться в сторону направления воздействия. Если ее переместить в горизонтальной плоскости в другой конец судна, лодка начнёт также поворачиваться, но направление вращения изменится. Отсюда можно сделать вывод, что существует такая точка приложения силы, точнее, линия, при воздействии на которую лодка не изменит своего положения, то есть плавательное средство начнёт двигаться ускоренно поступательно. Допустим, это будет сила F3.

Логично, что можно подобрать и другую силу, вызывающую поступательное прямолинейное перемещение, например, F4.

При этом точку воздействия можно перемещать по линии её направления, так как, согласно правилу, величина действия при этом не изменяется. В итоге получится точка, где пересекутся приложенные силы F3 и F4. Таких моментов можно приложить сколько угодно, при этом они все соединятся в одном месте. Точку пересечения линий действия сил, которые вызывают ускоренное поступательное движение тела, называют центром масс.

На лодку действует ещё одна сила — притяжения. На самом деле она воздействует на каждую частичку объекта, поэтому на тело одновременно оказывает влияние огромное количество моментов. Это множество и принято заменять их равнодействующей — то есть силой, приложенной к центру тяжести. В физике параметр обозначают как mg. Другими словами, это точка приложения равнодействующих сил тяжести.

Существует взаимосвязь между массой и тяжестью. Если тело разбить на кусочки и бросить их, скорость падения будет для всех тел одинаковой, так как ускорение не зависит от массы. При этом падающий объект движется поступательно.

А значит, приложенная сила проходит через центр масс, то есть через центр тяжести, поэтому несмотря на разный принцип определения этих точек, их положение совпадает.

Поиск центра тяжести

Чтобы определить центр тяжести для тела сложной формы, его нужно разделить на простые фигуры и определить точки равновесия для каждой из них. Для простых геометрических объектов используют симметрию. Например, в шаре параметр располагается в центре, в однородном цилиндре — в точке на середине оси. Частным случаем разбиения фигуры при определении является метод отрицательных площадей. Его применяют к телам, которые имеют вырезы, и при этом площадь удалённой части известна.

Вот формулы для вычисления центра в некоторых фигурах:

В треугольнике: x = (1/3) * (x1 + x2 + x3); y = (1/3) * (y1 + y2 + y3). Физически центр находится в точке пересечения медиан и представляет собой среднее арифметическое из координат вершин.
В прямоугольнике: x = b/2; y = h/2. Центр равновесия располагается в точке пересечения диагональных прямых.
В полукруге: x =D/2; y = 4R/3π. Искомая точка лежит на оси симметрии.
В круге: x = R; y = R. Точка тяжести находится в центре фигуры.

Стоит отметить, что центр тяжести объёмных тел может находиться и вне фигуры, например, как у кольца. Вообще же для трёхмерного пространства, как учат на уроках физики в 7 классе, центр тяжести тела вычисляют по формулам: x = (ΣΔ m * x) / m; y = (ΣΔ m * y) / m; z = (ΣΔ m * z) / m, где: m — масса тела, x, y, z — координаты искомой точки в пространстве. Уравнение можно переписать и в векторной форме: r = (1 / m) Σm * r, где r — радиус вектор.

Существует и ряд теорем, благодаря которым можно определить точку массы в теле:

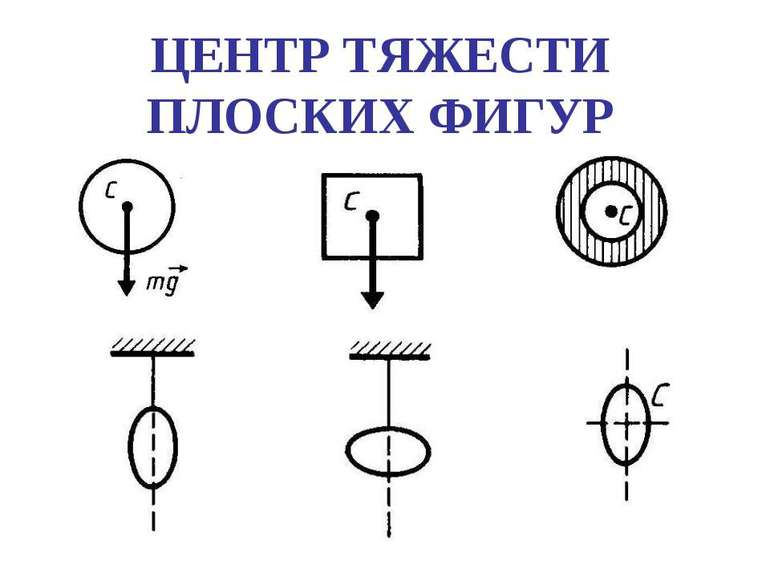
При рассмотрении однородного тела, имеющего плоскость симметрии, центр массы будет находиться в этой плоскости.
Если однородное тело обладает осью симметрии, центр располагается на ней.
Центр симметрии однородной фигуры совпадает с центром массы.
Центр масс симметричных фигур находится в их геометрическом центре.

Точку равновесия фигуры можно находить и через объём: R = (1 / V) * ∫ ∫ ∫rdV. Для плоских объектов используется формула R = (1 / S) * ∫ ∫ ∫rdS, а однородной линии R = (1 / L) * ∫ ∫ ∫rdL. Стоит отметить, что понятие точки тяжести применимо только к твёрдым объектам. Если это не так, использование понятия не имеет смысла.

Пример задания

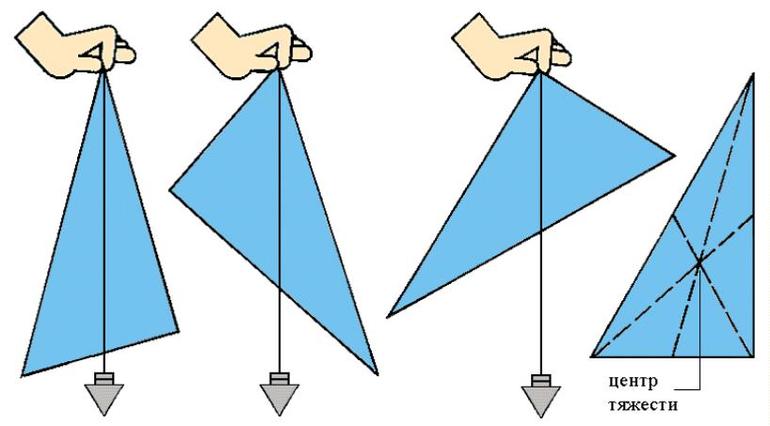
Теоретический материал лучше всего усваивается на практических заданиях. Не исключение и понятие о центре тяжести. Тема несложная, но при нахождении параметра желательно фигуру изобразить на рисунке.

Наиболее часто ученикам преподаватель предлагает решить задачу о нахождении центра масс сложного тела, но при этом достаточно симметричного. Например, пусть имеется диск из однородной пластины, в котором вырезан кусок треугольной формы. Необходимо найти центр равновесия оставшегося объекта.

Если нарисовать условие задачи, станет понятно, что треугольник прямоугольный, а центр масс находится на горизонтальной прямой, проходящей через середину диска. Пусть это будет ось x. Чтобы решить задачу, нужно разбить сложную фигуру на несколько частей, в каждой из которых можно найти искомую точку.

Симметрично удалённому треугольнику можно выделить аналогичную часть. В итоге останется круг с вырезанным внутри квадратом. Точка масс диска находится в центре. Для удобства её можно обозначить как x1. Вторая фигура — это треугольник. Точка равновесия у него находится на пересечении медиан. То есть на 1/3 высоты. Обозначить точку можно как x2.

Если масса треугольника равна М2, а круга М1, искомую координату можно определить по формуле: x = (m1x1 + m2x2) / m1 + m2. Далее, нужно найти, чему равняется сторона вырезанного треугольника. Из рисунка можно понять, что это расстояние будет r * √2, где r — радиус диска.

Теперь можно найти, чему будут равны x1 и x2. x1 будет равняться нулю, так как эту точку можно принять за начало координат. x2 же будет равняться 1/3 длины медианы. Высота фигуры совпадает с радиусом диска, значит: x2 = R/3.

В таких задачах самое сложное — это найти массы. Первую можно определить исходя из того, что она будет равняться массе диска минус значение квадрата. Так как фигура однородная, масса прямо пропорциональна площади. Тогда для первого участка m1 = σ * S = σ * (Sкруга — Sквадрата) = σ * (pR2 — 2R2) = σR2 * (p — 2), где: σ - поверхностная площадь. Соответственно, m2 = σ * Sтреугольника = σ * R2. Все найденные величины нужно подставить в формулу и найти ответ: x = ((r * σ * R 2 /3)) / (σ * R2 * (p — 2) + σ * R2) = (r / 3 (p — 1)). Это и будет искомая координата.

Простая задачка

Пусть имеются 2 шара. Они расположены так, что соприкасаются друг с другом. Сделаны тела из одного материала, но при этом радиусы у них отличаются вдвое. Значение первого равняется r = 20 см, а второго 40, то есть 2r. Найти, где находится точка равновесия такого объекта. Такого рода задачи обычно любят демонстрировать на презентациях, касающихся темы. Задача простая, но между тем помогает понять принцип нахождения центра равновесия.

Итак, при решении нужно будет воспользоваться формулой: x = (m1x1 + m2x2) / m1 + m2. Так как по условию радиусы шаров отличаются вдвое, их массы будут отличаться в 8 раз. Объём всегда пропорционален кубу линейных размеров.

Массу первого шара можно обозначить как m, а второго — 8m. Начало координат для удобства лучше поместить в центр меньшей фигуры. В результате середина большого шара будет иметь координату 3r. Значит, искомая координата равняется: x = ((m* 0 + 8m * 3r)) / (m + 8m) = (8 * 3r) / 9 = 8r/3.

То есть нужная точка находится на расстоянии 1/3 радиуса ближе к маленькому шару (если отсчитывать от середины большого).

Читайте также: