Законы алгебры логики кратко

Обновлено: 05.07.2024

1. Переместительный, или закон коммутативности для операций сложения и умножения, соответственно:

A Ú B = B Ú A;

A B = B A.

2. Сочетательный, или закон ассоциативности для сложения и умножения, соответственно:

(A Ú B) Ú C = A Ú (B Ú C);

(A B) C = A (B C).

3. Распределительный, или закон дистрибутивности для сложения и умножения, соответственно:

(A Ú B) C = A C Ú B·C;

(A B) Ú C = (A Ú C) (B Ú C).

4. Закон двойственности или инверсии (правило де Моргана) для логических операций сложения и умножения, соответственно:

Благодаря этим правилам появилась возможность выражать дизъюнкцию через конъюнкцию и отрицание, а конъюнкцию – через дизъюнкцию и отрицание. Законы двойственности справедливы для любого числа переменных.

Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей, описываемых законом, или с помощью логических преобразований.

Эти правила широко используют для преобразования переключательных функций с целью их упрощения.

Формы переключательной функции являются двойственными, если одна получается из другой путем замены всех символов операции И на символы операции ИЛИ и наоборот; всех нулей на единицы и наоборот. Например, для функции

двойственной функцией будетY_ДВ = = = .

В булевой алгебре при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее конъюнкции, затем – дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий: в первую очередь должны выполняться операции внутри скобок.

Тождества и правила

Для преобразований логических выражений пользуются легко доказываемыми тождествами (таблица 3.1):

Таблица 3.1– Набор логических тождеств

А Ú 0 = А	А Ú = 1	А·А = А
А Ú 1 = 1	А·0 = 0	А· = А
А Ú А = А	А·1 = 1	= А

С помощью законов алгебры логики и тождеств могут быть доказаны соотношения, получившие названия правил:

поглощения A Ú A×B = A, A×(1 Ú B) = A,

склеивания: А·ВÚ А = А; (А·Ú В )(А +) = А.

Доказать справедливость этих соотношений можно путем следующих преобразований:

А Ú A×B = A – доказательство A + A×B = А (1 + В) = А·1 = А;

A×(A Ú B) = A – A×(A Ú B) = А А + А В = А + А В = А;

(А·Ú В )(А + ) = А – (А·Ú В )(А + ) = А А + А +В А +В =

= А (1 + + В + 0) = А.

Эти правила широко используют для преобразования переключательных функций с целью их упрощения.

Двойственная функция F_ДВ =

Первыми, как и в арифметике, выполняются действия внутри скобок. В булевой алгебре при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее конъюнкции, затем – дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий: в первую очередь должны выполняться операции внутри скобок.

3.4 Элементарные логические функции.

Совокупность различных значений переменных называют набором. Булева функция n аргументов может иметь до N = 2 n наборов. Поскольку функция принимает только два значения, общее число булевых функций n аргументов равно 2 N = 2 2 n . Таким образом, функция одного аргумента может иметь четыре значения:

f₁ = А, f₂= , f₃ = 1 (константа 1), f₄ = 0 (константа 0).

Два аргумента дают 16 значений функции (таблица 3.3.).

Любая из этих функций обращается в единицу (конституента единицы) только на своем наборе, во всех остальных случаях (2 n – 1) она равна нулю. Функции взаимно инверсны, если на том же наборе функции обращается в нуль (конституента нуля), а в остальных случаях она равна единице.

В число шестнадцати функций входят и вырожденные функции:

f₀ = 0 – константа 0; f₁₅ = 1 – константа 1;

f₃ = a – переменная a; f ₅ = b – переменная b;

f₁₂ = – инверсия a; f₁₀ = – инверсия b.

Остальные десять булевых функций сведены в таблицу 3.4.

Кратко рассмотрим работу логических элементов, которые не были описаны выше.

Особенностью функции является то, что высокий уровень H на выходе устанавливается лишь при наличии низких уровней L на всех входах.

Следующая функциональная схема – логическое И-НЕ (штрих Шеффера, NAND gate) f₇ = . Если на любой из входов подан низкий уровень напряжения, то на выходе устанавливается высокий уровень напряжения (табл. на рис. 3.7, а). Там же приведены УГО логическое И-НЕ и эпюры напряжений входах и выходах схемы (рис. 3.7, а и3.7, б,соответственно).

Особенностью функции является то, что лог. 1 устанавливается на выходе при наличии хотя бы на одном из входов низкого уровня L.

Импликация от В к А

Импликация от b к a это дизъюнкция a и f₁₁ = . На рис. 3.8 а, б, в приведена таблица истинности (а), условное графическое обозначение (б) и эпюры напряжений (в).

Логический ноль на выходе устанавливается лишь в одном случае, когда a и принимают низкий уровень.

Равнозначность А и В

Равнозначность указывает на то, что оба аргумента имеют одинаковый (высокий H или низкий L) уровень. Таблица истинности, условное графическое обозначение и зпюры напряжений приведены на рис. 3.9 а, б, в, соотвтственно.

Свойства двойственности переключательных функций широко используются при проектировании электронных устройств. Как уже указывалось, функцию алгебраического умножения всегда можно заменить функцией алгебраического сложения, используя правило отрицания (де Моргана).

Взаимно инверсные функции сведены в табл. 3.4.

Первая пара двойственных функций относится к дизъюнкциям.

Функция Пирса f₁ = инверсна по отношению к функции дизъюнкции f₁₄ = , .

Функция Шеффера f₇ = инверсна по отношению к конъюнкции f₈ = a Ù b:

Функции запрета и импликации также инверсны по отношению друг к другу:

Взаимно инверсны функция неравнозначности (сложения по модулю два) f₆ = и функция равнозначности f₉ =

Для доказательства этого равенства воспользуемся правилом де Моргана:

С помощью одного и двух переменных, называемых элементарными логическими функциями, можно, используя принцип суперпозиции, т.е. принцип подстановки булевых функций вместо аргументов в другую функцию, можно построить булеву функцию любой сложности.

В алгебре логики имеется четыре основных закона:

1. Переместительный, или закон коммутативности для операций сложения и умножения, соответственно:

A Ú B = B Ú A;

A B = B A.

2. Сочетательный, или закон ассоциативности для сложения и умножения, соответственно:

(A Ú B) Ú C = A Ú (B Ú C);

(A B) C = A (B C).

3. Распределительный, или закон дистрибутивности для сложения и умножения, соответственно:

(A Ú B) C = A C Ú B·C;

(A B) Ú C = (A Ú C) (B Ú C).

Эти правила широко используют для преобразования переключательных функций с целью их упрощения.

двойственной функцией будетY_ДВ = = = .

Тождества и правила

Для преобразований логических выражений пользуются легко доказываемыми тождествами (таблица 3.1):

Таблица 3.1– Набор логических тождеств

А Ú 0 = А	А Ú = 1	А·А = А
А Ú 1 = 1	А·0 = 0	А· = А
А Ú А = А	А·1 = 1	= А

С помощью законов алгебры логики и тождеств могут быть доказаны соотношения, получившие названия правил:

поглощения A Ú A×B = A, A×(1 Ú B) = A,

склеивания: А·ВÚ А = А; (А·Ú В )(А +) = А.

Доказать справедливость этих соотношений можно путем следующих преобразований:

А Ú A×B = A – доказательство A + A×B = А (1 + В) = А·1 = А;

A×(A Ú B) = A – A×(A Ú B) = А А + А В = А + А В = А;

(А·Ú В )(А + ) = А – (А·Ú В )(А + ) = А А + А +В А +В =

= А (1 + + В + 0) = А.

Эти правила широко используют для преобразования переключательных функций с целью их упрощения.

Двойственная функция F_ДВ =

3.4 Элементарные логические функции.

f₁ = А, f₂= , f₃ = 1 (константа 1), f₄ = 0 (константа 0).

Два аргумента дают 16 значений функции (таблица 3.3.).

В число шестнадцати функций входят и вырожденные функции:

f₀ = 0 – константа 0; f₁₅ = 1 – константа 1;

f₃ = a – переменная a; f ₅ = b – переменная b;

f₁₂ = – инверсия a; f₁₀ = – инверсия b.

Остальные десять булевых функций сведены в таблицу 3.4.

Кратко рассмотрим работу логических элементов, которые не были описаны выше.

Импликация от В к А

Логический ноль на выходе устанавливается лишь в одном случае, когда a и принимают низкий уровень.

Равнозначность А и В

Взаимно инверсные функции сведены в табл. 3.4.

Первая пара двойственных функций относится к дизъюнкциям.

Функция Пирса f₁ = инверсна по отношению к функции дизъюнкции f₁₄ = , .

Функция Шеффера f₇ = инверсна по отношению к конъюнкции f₈ = a Ù b:

Функции запрета и импликации также инверсны по отношению друг к другу:

Взаимно инверсны функция неравнозначности (сложения по модулю два) f₆ = и функция равнозначности f₉ =

Для доказательства этого равенства воспользуемся правилом де Моргана:

Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.

При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.

Законы алгебры высказываний (алгебры логики) — это тавтологии.

Иногда эти законы называются теоремами.

В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.

Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.

Закон тождества:

Всякое понятие и суждение тождественно самому себе.

Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.

Закон непротиворечия :

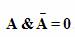
В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:

1. Число 12345 либо четное, либо нечетное, третьего не дано.

2. Предприятие работает убыточно или безубыточно.

3. Эта жидкость является или не является кислотой.

Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.

Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.

Например, определим, чему эквивалентно (равносильно) А (двойное отрицание А , т. е. отрицание отрицания А ).Для этого построим таблицу истинности:

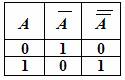
По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.

Таким образом, мы можем сформулировать закон двойного отрицания:

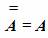
Если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание. Например, высказывание А = Матроскин — кот эквивалентно высказыванию А = Неверно, что Матроскин не кот .

Аналогичным образом можно вывести и проверить следующие законы:

Свойства констант:

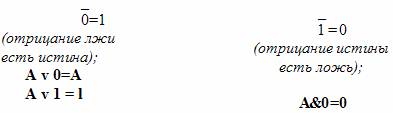
Законы идемпотентности:

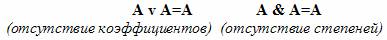
Сколько бы раз мы ни повторяли: телевизор включен или телевизор включен или телевизор включен . значение высказывания не изменится. Аналогично от повторения на улице тепло, на улице тепло. ни на один градус теплее не станет.

Законы коммутативности:

Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.

Законы ассоциативности:

A v(B v C) = (A v B) v C;

А & (В & C) = (A & В) & С.

Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.

Законы дистрибутивности:

A v (B & C) = (A v B) &(A v C)

(дистрибутивность дизъюнкции
относительно конъюнкции)

А & (B v C) = (A & B) v (А & C)

(дистрибутивность конъюнкции
относительно дизъюнкции)

Закон дистрибутивности конъюнкции относительно дизъюнкции аналогичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:

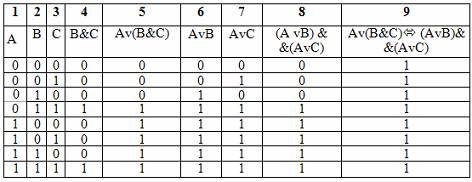
Законы поглощения:

Проведите доказательство законов поглощения самостоятельно.

Законы де Моргана:

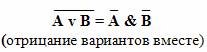
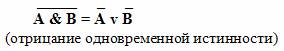
Словесные формулировки законов де Моргана:

Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.

Примеры выполнения закона де Моргана:

1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.

2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.

Замена операций импликации и эквивалентности

Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.

Так, заменить операцию импликации можно в соответствии со следующим правилом:

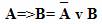
Для замены операции эквивалентности существует два правила:

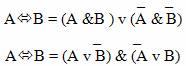
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.

Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.

Способ определения истинности сложного выражения путём построения таблиц истинности становится громоздким при возрастании количества логических переменных, так как число наборов резко увеличивается. В таких случаях используют способы упрощения формул путём применения равносильных преобразований. Ниже в таблице приведены основные законы алгебры логики.

Выполняется закон двойственности: если конъюнкцию заменить дизъюнкцией, дизъюнкцию заменить конъюнкцией, 0 заменить на 1, а 1 на 0, то равносильность, записанная для дизъюнкции, перейдёт в равносильность, записанную для конъюнкции.

Выражение имеет нормальную форму, если в нём используются только операции дизъюнкции, конъюнкции и отрицания переменных. При этом не используются двойное отрицание и отрицание выражений.

Для приведения выражения к нормальной форме в первую очередь избавляются от отрицаний выражений, операций импликации, эквиваленции и исключающего или. Затем используют законы алгебры логики для уменьшения количества вхождений переменных.

Применение законов алгебры логики, похожих на законы преобразований в обычной алгебре, не вызывает затруднений. Рассмотрим примеры применения законов склеивания, поглощения, идемпотентности, законов де Моргана, не имеющих аналогов в обычной алгебре.

Упростить выражение X & Y & Z ∨ ¬X & Y & Z . В выражении X & Y & Z ∨ ¬X & Y & Z переменной А соответствует переменная X , переменной В соответствует выражение Y & Z . Тогда в результате упрощения получим

Но если использовать закон идемпотентности А = А ∨ А , можно в исходную формулу добавить ещё два слагаемых, совпадающих с первым. Получим

Упростить выражение X ∨ X & Y ∨ X & Z ∨ X & Y & Z . Для всех слагаемых общим сомножителем является X . Последовательно применяя закон поглощения А ∨ А & В = А , получим

В предпоследней строке к выражению Z ∨ ¬X & Y & Z был применён закон поглощения А ∨ А & В = А .
3. Упростить выражение (X ∨ Y) & (X ∨ Y ∨ Z) & (X ∨ Y ∨ ¬Z) . Для всех сомножителей общим слагаемым является X ∨ Y , это и есть результат упрощения.

Совет: В операциях конъюнкции и дизъюнкции имена переменных записывайте в алфавитном порядке, причём сначала переменную, а затем её отрицание.

Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.

Что такое алгебра и алгебра логики

Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.

Законы алгебры логики

Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.

Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.

Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.

Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.

Основные законы алгебры логики представлены в таблице:

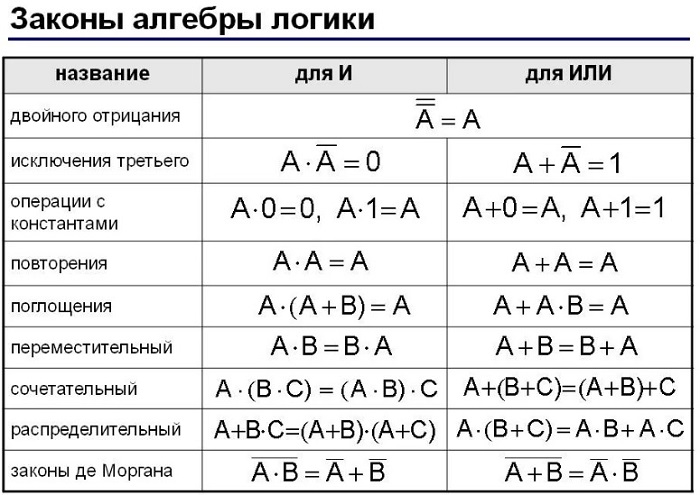
Логические выражения

В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.

Нью-Йорк — столица США (ложное);

в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.

Идёт дождь, а у меня нет зонта.

Основные логические операции

Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.

Логическое отрицание (инверсия) —НЕ

Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).

Таблица истинности инверсии:

Результаты операции НЕ следующие:

если исходное выражение истинно, то результат его отрицания будет ложным;

если исходное выражение ложно, то результат его отрицания будет истинным.

Логическое сложение (дизъюнкция, объединение) — ИЛИ

Таблица истинности операции ИЛИ:

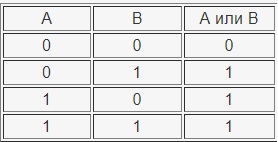
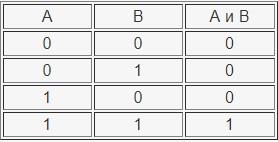
Логическое умножение(конъюнкция) — И

В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.

За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).

При всех остальных значениях операция будет ложной.

Таблица истинности операции И приведена ниже:

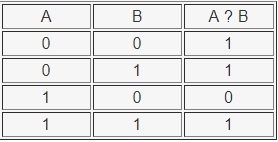
Логическое следование (импликация) — ЕСЛИ ТО

Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.

Таблица истинности операции ЕСЛИ ТО выглядит так:

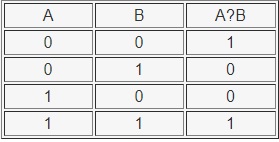
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В

Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.

И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.

Таблица истинности операции эквивалентности:

Читайте также: