Закон моргана информатика кратко и понятно
Обновлено: 05.07.2024
Законы де Моргана – это логические правила, установленные шотландским математиком Огастесом де Морганом, связывающие пары логических операций при помощи логического отрицания.
Огастес де Морган заметил, что в классической логике справедливы следующие соотношения:
not ( А and В ) = (not А ) or (not В )
not ( А or В ) = (not А ) and (not В )
В более привычной для нас форме данные соотношения можно записать в следующем виде:
Законы де Моргана можно сформулировать следующим образом:
I закон де Моргана: Отрицание дизъюнкции двух простых высказываний равносильно конъюнкции отрицаний этих высказываний.
II закон де Моргана: Отрицание конъюнкции двух простых высказываний равносильно дизъюнкции отрицаний этих высказываний.
Рассмотрим применение законов де Моргана на конкретных примерах.
Пример 1. Преобразовать формулу так, чтобы не было отрицаний сложных высказываний.
Воспользуемся первым законом де Моргана, получим:
к отрицанию конъюнкции простых высказываний В и С применим второй закон де Моргана, получим:
В итоге мы получили равносильное высказывание, в котором нет отрицаний составных высказываний, а все отрицания относятся только к простым высказываниям.
Проверить справедливость решения можно с помощью таблиц истинности. Для этого составим таблицы истинности для исходного высказывания:
и для высказывания, полученного в результате преобразований, выполненных с помощью законов де Моргана:
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
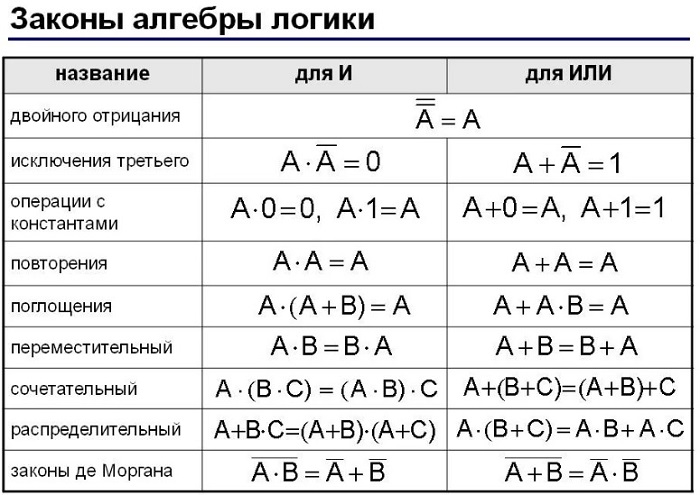
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Таблица истинности операции ИЛИ:
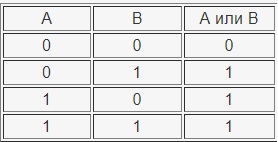
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
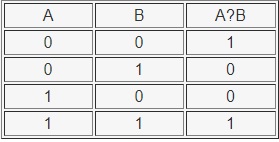
Таблица истинности операции И приведена ниже:
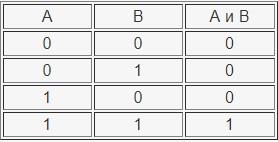
Логическое следование (импликация) — ЕСЛИ ТО
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
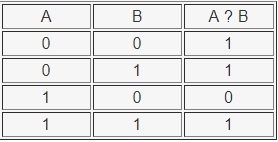
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
Огастес де Морган первоначально заметил, что в классической пропозициональной логике справедливы следующие соотношения:
not (P and Q) = (not P) or (not Q) not (P or Q) = (not P) and (not Q)
Обычная запись этих законов в формальной логике:






История
Ссылки
- Weisstein, Eric W.Законы де Моргана (англ.) на сайте Wolfram MathWorld.
- Булева алгебра
- Законы логики
- Математическая логика
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое "Законы де Моргана" в других словарях:
ЗАКОНЫ ДЕ МОРГАНА — законы логики высказываний, связывающие отрицание с операциями конъюнкции и дизъюнкции, соответствующими логич. союзам и и неразделительному или естеств. языка. З. де М. в словесной формулировке были известны еще схоластич. логикам. В математич.… … Философская энциклопедия
Законы Моргана — * законы Моргана * Morgan’s Laws … Генетика. Энциклопедический словарь
Моргана законы — * Моргана законы * Morgan’s Laws or M. rules основные положения хромосомной теории наследственности, разработанные Т. Морганом и сотр. в 1911 1915 гг. Сводятся к следующему: 1) гены находятся в хромосомах и в пределах одной хромосомы образуют… … Генетика. Энциклопедический словарь
Моргана единица морганида М — Моргана единица, морганида, М * Моргана адзінка, марганіда, М * Morgan’s unit or M относительное расстояние между двумя генами на хромосоме, или частота рекомбинации () между двумя генетическими маркерами. Одна морганида соответствует 100%… … Генетика. Энциклопедический словарь
МОРГАНА ЗАКОНЫ — Предусматривают, что: гены находятся в хромосомах, и в пределах одной хромосомы образуют одну группу сцепления; гены в хромосомах расположены линейно; между гомологичными хромосомами в мейозе может происходить кроссинговер, частота которого пропо … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
законы Моргана — Ряд закономерностей наследования, иногда объединяемых в общую группу З.М.: вхождение генов в хромосомы, представляющие собой группы сцепления, линейное расположение генов в хромосомах и наличие между гомологичными хромосомами мейотической… … Справочник технического переводчика
Законы Хаммурапи — Свод законов Хаммурапи (или Кодекс Хаммурапи), созданный приблизительно в 1780 г. до н. э., является одним из древнейших законодательных памятников. Найден археологической экспедицией Жака де Моргана в ходе раскопок в 1901 1902 годах в Сузах… … Википедия
Законы Хамураппи — Свод законов Хаммурапи (или Кодекс Хаммурапи), созданный приблизительно в 1780 г. до н. э., является одним из древнейших законодательных памятников. Найден археологической экспедицией Жака де Моргана в ходе раскопок в 1901 1902 годах в Сузах… … Википедия
Законы царя Хамураппи — Свод законов Хаммурапи (или Кодекс Хаммурапи), созданный приблизительно в 1780 г. до н. э., является одним из древнейших законодательных памятников. Найден археологической экспедицией Жака де Моргана в ходе раскопок в 1901 1902 годах в Сузах… … Википедия
законы Моргана — Morgan rules законы Моргана. Pяд закономерностей наследования, иногда объединяемых в общую группу З.М.: вхождение генов в хромосомы, представляющие собой группы сцепления, линейное расположение генов в хромосомах и наличие между гомологичными… … Молекулярная биология и генетика. Толковый словарь.
Лглаза Моргана это правила вывода, используемые в логике высказываний, которые устанавливают, что является результатом отрицания дизъюнкции и конъюнкции высказываний или переменных высказываний. Эти законы были определены математиком Августом Де Морганом..
Законы Моргана представляют собой очень полезный инструмент, чтобы продемонстрировать обоснованность математических рассуждений. Позже они были обобщены в рамках концепции множеств математиком Джорджем Булем.

Это обобщение, сделанное Булем, полностью эквивалентно начальным законам Моргана, но оно разработано специально для множеств, а не для предложений. Это обобщение также известно как законы Моргана.
- 1 Обзор логики высказываний
- 1.1 Ошибка
- 1.2 Предложения
- 2.1 Демонстрация
- 3.1 Объединение, пересечение и дополнение множеств
Обзор логики высказываний
Прежде чем посмотреть, какие конкретно законы Моргана и как они используются, удобно вспомнить некоторые базовые понятия логики высказываний. (Более подробно см. Статью по логике высказываний).
В области математической (или пропозициональной) логики логический вывод - это вывод, который выводится из ряда предпосылок или гипотез. Этот вывод вместе с упомянутыми предпосылками приводит к так называемым математическим рассуждениям.
Это рассуждение должно быть в состоянии быть продемонстрировано или опровергнуто; то есть, что не все выводы или выводы в математических рассуждениях являются действительными.
ошибочность
Ложный вывод, основанный на определенных предположениях, которые считаются истинными, называется ошибкой. Ошибки имеют особенность того, что аргументы кажутся правильными, но математически они не.
Логика высказываний отвечает за точную разработку и предоставление методов, с помощью которых можно без какой-либо двусмысленности подтвердить или опровергнуть математические рассуждения; то есть, сделать правильный вывод из помещения. Эти методы известны как правила вывода, частью которых являются законы Моргана..
предложения
Существенными элементами логики высказываний являются высказывания. Предложения - это утверждения, о которых можно сказать, являются ли они действительными или нет, но что они не могут быть истинными или ложными одновременно. Не должно быть никакой двусмысленности в этом вопросе.
Чтобы работать более широко, вместо рассмотрения конкретных предложений, мы рассматриваем пропозициональные переменные, которые представляют любые предложения и обычно обозначаются строчными буквами p, q, r, s и т. Д..
Пропозициональная формула - это комбинация пропозициональных переменных через некоторые из логических связок. Другими словами, это композиция пропозициональных переменных. Они обычно обозначаются греческими буквами.
Говорят, что пропозициональная формула логически подразумевает другую, когда последняя верна каждый раз, когда первая верна. Это обозначается как:
![]()
Когда логическая импликация между двумя пропозициональными формулами является взаимной, то есть когда предыдущая импликация действительна и в противоположном направлении, формулы называются логически эквивалентными, и они обозначаются как
![]()
Логическая эквивалентность является своего рода равенством между пропозициональными формулами и позволяет при необходимости заменять одно на другое..
Законы Моргана
Законы Моргана состоят из двух логических эквивалентностей между двумя пропозициональными формами, а именно:
![]()
Эти законы позволяют отделить отрицание дизъюнкции или конъюнкции как отрицание вовлеченных переменных.
Первое можно прочитать следующим образом: отрицание дизъюнкции равно соединению отрицаний. И второе звучит так: отрицание соединения - это дизъюнкция отрицания.
Другими словами, отрицать дизъюнкцию двух пропозициональных переменных эквивалентно соединению отрицаний обеих переменных. Аналогичным образом, отрицать конъюнкцию двух пропозициональных переменных равносильно дизъюнкции отрицаний обеих переменных.
Как упоминалось ранее, замена этой логической эквивалентности помогает продемонстрировать важные результаты, наряду с другими существующими правилами вывода. С их помощью вы можете упростить многие пропозициональные формулы, чтобы они были более полезными для работы.
Ниже приведен пример математического доказательства с использованием правил вывода, среди этих законов Моргана. В частности, показано, что формула:
![]()
![]()
Последнее проще понять и развить.
шоу
![]()
Стоит отметить, что законность законов Моргана может быть продемонстрирована математически. Одним из способов является сравнение ваших таблиц истинности.
наборы
Те же правила вывода и понятия логики, применяемые к высказываниям, также могут быть разработаны с учетом множеств. Это то, что известно как булева алгебра, после математика Джорджа Буля.
Чтобы дифференцировать случаи, необходимо изменить обозначения и перенести в множества все понятия, уже виденные в логике высказываний..
Набор представляет собой набор объектов. Наборы обозначаются заглавными буквами A, B, C, X, . а элементы набора обозначаются строчными буквами a, b, c, x и т. Д. Когда элемент a принадлежит множеству X, он обозначается как:
![]()
Когда он не принадлежит X, обозначение:
![]()
Способ представления наборов - размещение их элементов внутри ключей. Например, набор натуральных чисел представлен:
![]()
![]()
Например, набор целых чисел больше -4 может быть выражен как:
![]()
Или эквивалентно и более сокращенно, как:
![]()
Аналогично, следующие выражения представляют наборы четных и нечетных чисел соответственно:
![]()
Объединение, пересечение и дополнение множеств
Далее мы увидим аналоги логической связки в случае множеств, которые являются частью основных операций между множествами.
Союз и пересечение
Объединение и пересечение множеств определяются соответственно следующим образом:
![]()
Например, рассмотрим наборы:
![]()
Затем вы должны:
![]()
дополнение
Дополнение набора состоит из элементов, которые не принадлежат этому набору (того же типа, что и оригинал). Дополнение множества A обозначается как:
![]()
Например, в натуральных числах набор четных чисел является дополнением нечетных чисел, и наоборот.
Чтобы определить дополнение набора, необходимо с самого начала очистить универсальный или основной набор элементов, которые рассматриваются. Например, это не равно, чтобы рассмотреть дополнение набора на натуральных числах, что на рациональных.
В следующей таблице показано отношение или аналогия, которая существует между операциями над ранее определенными наборами и связующими из логики высказываний:
![]()
Законы Моргана для множеств
Наконец, законы Моргана о множествах таковы:
![]()
На словах: дополнение объединения - это пересечение дополнений, а дополнение пересечения - это объединение дополнений.
Читайте также:




















