Закон де моргана кратко

Обновлено: 05.07.2024

На вводном уроке, посвящённом основам математической логики, мы познакомились с базовыми понятиями этого раздела математики, и сейчас тема получает закономерное продолжение. Помимо нового теоретического, а точнее даже не теоретического – а общеобразовательного материала нас ожидают практические задания, и поэтому если вы зашли на данную страницу с поисковика и/или плохо ориентируетесь в материале, то, пожалуйста, пройдите по вышеуказанной ссылке и начните с предыдущей статьи. Кроме того, для практики нам потребуется 5 таблиц истинности логических операций, которые я настоятельно рекомендую переписать от руки.

НЕ запомнить, НЕ распечатать, а именно ещё раз осмыслить и собственноручно переписать на бумагу – чтобы они были перед глазами:

– таблица НЕ;
– таблица И;
– таблица ИЛИ;
– импликационная таблица;
– таблица эквиваленции.

На самом деле с понятием логической формулы вы уже знакомы. Приведу стандартное, но довольно-таки остроумное определение: формулами алгебры высказываний называются:

1) любые элементарные (простые) высказывания ;

2) если и – формулы, то формулами также являются выражения вида
.

Никаких других формул нет.

Логическую формулу можно рассматривать, как логическую функцию. Запишем в функциональном виде ту же конъюнкцию:

Элементарные высказывания и в этом случае играют роль аргументов (независимых переменных), которые в классической логике могут принимать 2 значения: истина или ложь. Далее для удобства я буду иногда называть простые высказывания переменными.

– в первую очередь выполняется отрицание ;
– во вторую очередь – конъюнкция ;
– затем – дизъюнкция ;
– потом импликация ;
– и, наконец, низший приоритет имеет эквиваленция .

Наверное, все понимают, но на всякий пожарный: и – это две разные формулы! (как в формальном, так и в содержательном плане)

(три горизонтальные чёрточки – это значок тождества)

Составить таблицу истинности для формулы и убедиться в справедливости знакомого вам тождества .

Ещё раз повторим порядок решения задачи:

1) Так как в формулу входят две переменные, то всего будет 4 возможных набора нулей и единиц. Записываем их в оговорённом выше порядке.

И, наконец, сверяемся с таблицей истинности эквиваленции .

Основные равносильности алгебры высказываний

С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:

Коммутативность конъюнкции и коммутативность дизъюнкции

Коммутативность – это перестановочность:

Ассоциативность логического умножения и сложения

Дистрибутивные свойства

Закон идемпотентности

Что делать, латынь.

И тут же несколько похожих тождеств:

…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)

Закон двойного отрицания

Законы поглощения

В правом тождестве скобки можно опустить.

Законы де Моргана

Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если – Студент ответил на 1-й вопрос и – Студент ответил на 2-й вопрос. Тогда высказывание , гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению – Студент не ответил на 1-й вопрос или на 2-й вопрос.

Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.

Теперь убедимся, например, в справедливости закона де Моргана .

Доказать следующие равносильности:

Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!

Продолжаем знакомиться с законами логики!

Да, совершенно верно – мы с ними уже вовсю работаем:

Формула, которая принимает значение Истина при любом наборе значений входящих в неё переменных, называется тождественно истинной формулой или законом логики.

В силу обоснованного ранее перехода от равносильности к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.

Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных, называется тождественно ложной формулой или противоречием.

Фирменный пример противоречия от древних греков:
– никакое высказывание не может быть истинным и ложным одновременно.

Однако и любое противоречие – это тоже закон логики, в частности:

Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:

Закон исключённого третьего

Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.

Закон контрапозиции

Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.

Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной:

Закон силлогизма

Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)

Давайте на этой веселой ноте проведём доказательство. В данную формулу входят уже элементарных высказывания , а значит, всего будет: различных комбинаций нулей и единиц (см. три левых столбца таблицы). Заодно, кстати, записал вам общую формулу; с точки зрения комбинаторики, здесь размещения с повторениями.

Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:

1) выполняем импликации и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;

2) к столбцам применяем правило И;

3) вот теперь выполняем ;

4) и на завершающем шаге применяем импликацию к столбцам и .

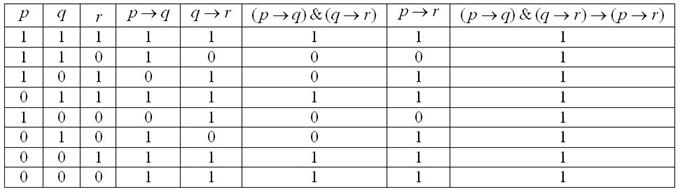
Не стесняйтесь контролировать процесс указательным и средним пальцем :))

Из последнего столбца, думаю, всё понятно без комментариев:
, что и требовалось доказать.

Выяснить, будет ли являться законом логики следующая формула:

Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.

Преобразование логических формул

Кроме того, есть ещё одна важная вещь: тождества справедливы не только для элементарных высказываний, но и для произвольных формул. Так, например:

, где – любые (сколь угодно сложные) формулы.

Преобразуем, например, сложную импликацию (1-е тождество):

Ну, а с коммутативностью вообще всё просто – даже обозначать ничего не нужно… что-то запал мне в душу закон силлогизма:))

Таким образом, закон можно переписать и в более затейливом виде:

В качестве тренировки упростим формулу .

Как правило, на первом шаге (шагах) избавляются от эквиваленции и импликации (если они есть) и сводят формулу к трём основным логическим операциям. Что тут скажешь…. Логично.

(1) Используем тождество . А нашем случае .

(2) К внешним скобкам применяем закон де Моргана , где .

(3) К внутренним скобкам применяем закон двойного отрицания . Внешние скобки можно убрать, т.к. за её пределами находятся равные по силе операции.

(4) В силу коммутативности дизъюнкции меняем местами и . Оставшиеся скобки тоже убираем по озвученной выше причине.

(5) В силу коммутативности дизъюнкции меняем местами и , а также и .

(6) Используем закон идемпотентности и закон исключенного третьего

(7) Дважды используем тождество

Вот оно как…, оказалось, что наша формула – тожественно истинна:

Желающие могут составить таблицу истинности и убедиться в справедливости данного факта.

Пара задач для закрепления материала:

Выразить эквиваленцию через отрицание, конъюнкцию, дизъюнкцию и раскрыть скобки

Аккуратно проводим преобразования в соответствии с равносильностями. После этого будет не лишним вернуться к параграфу об эквиваленции и найти там фразу, которая соответствует полученному результату ;-)

Упростить логическую формулу

Решения с подробными комментариями совсем близко.

Решения и ответы:

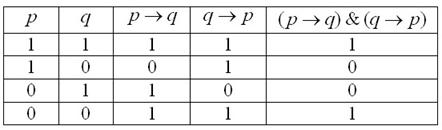
Задание 1 Решение: составим таблицу истинности для формулы :

(подробные инструкции по заполнению таблицы находятся после условия задачи)
Полученный результат совпадает с эквиваленцией высказываний и , таким образом:

Задание 2 Решение: доказательства проведём с помощью таблиц истинности:

а) Дважды записываем все варианты истины и лжи высказывания и применяем к столбцам операцию ИЛИ:

Результат совпадает с . Тождество доказано

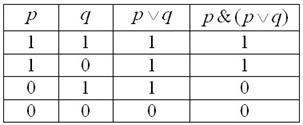
б) составим таблицу истинности для левой части тождества
. Сначала к столбцам и применяем операцию ИЛИ, затем к столбцам и – операцию И:

В результате истинность формулы совпала с истинностью высказывания , таким образом, тождество доказано.

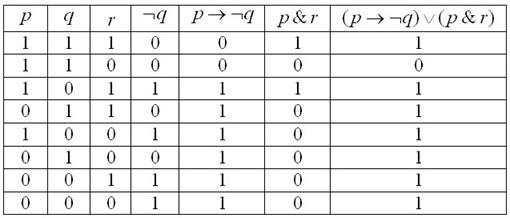
Задание 3 Решение: составим таблицу истинности:

Вывод: данная формула не является тождественно истинной (законом логики)

Задание 4 Решение:

(1) Используем тождество .
(2) Дважды применяем тождество .
(3) Используем дистрибутивный закон , в данном случае:
(квадратные скобки можно было не ставить – они не меняют порядок действий, но помогают лучше видеть ситуацию).
(4) В квадратных скобках используем коммутативность конъюнкции.
(5) Дважды используем тот же самый дистрибутивный закон.
(6) Во второй слева скобке используем коммутативность конъюнкции.
(7) Согласно закону противоречия: .
(8) К формуле дважды применяем тожество .
(9) А это уже для красоты :)) Скобки, кстати, можно было убрать намного раньше (я их не опускал с целью улучшить восприятие преобразований).

Задание 5 Решение:

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Законы де Моргана – это логические правила, установленные шотландским математиком Огастесом де Морганом, связывающие пары логических операций при помощи логического отрицания.

Огастес де Морган заметил, что в классической логике справедливы следующие соотношения:

not ( А and В ) = (not А ) or (not В )

not ( А or В ) = (not А ) and (not В )

В более привычной для нас форме данные соотношения можно записать в следующем виде:

Законы де Моргана можно сформулировать следующим образом:

I закон де Моргана: Отрицание дизъюнкции двух простых высказываний равносильно конъюнкции отрицаний этих высказываний.

II закон де Моргана: Отрицание конъюнкции двух простых высказываний равносильно дизъюнкции отрицаний этих высказываний.

Рассмотрим применение законов де Моргана на конкретных примерах.

Пример 1. Преобразовать формулу так, чтобы не было отрицаний сложных высказываний.

Воспользуемся первым законом де Моргана, получим:

к отрицанию конъюнкции простых высказываний В и С применим второй закон де Моргана, получим:

В итоге мы получили равносильное высказывание, в котором нет отрицаний составных высказываний, а все отрицания относятся только к простым высказываниям.

Проверить справедливость решения можно с помощью таблиц истинности. Для этого составим таблицы истинности для исходного высказывания:

и для высказывания, полученного в результате преобразований, выполненных с помощью законов де Моргана:

законы логики высказываний, связывающие отрицание с операциями конъюнкции и дизъюнкции, соответствующими логич. союзам "и" и неразделительному "или" естеств. языка. З. де М. в словесной формулировке были известны еще схоластич. логикам. В математич. логику введены англ. логиком де Морганом, однако не как законы логики высказываний, а как соответствующие законы логики классов. Имеют вид:

Здесь знак "" означает операцию отрицания, знак "/" – дизъюнкцию (неразделительное "или"), а знак "&" – конъюнкцию высказываний (союз "и"). Закон (1) читается: отрицание конъюнкции высказываний А и В эквивалентно (равносильно) дизъюнкции отрицаний этих высказываний; закон (2) читается: отрицание дизъюнкции высказываний А и В эквивалентно конъюнкции их отрицаний.

Лит.: Тарский Α., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948, с. 88; Чёрч Α., Введение в математическую логику, [т.] 1, пер. с англ., М., 1960, с. 98, 394; De Morgan Α., Formal logic. L., 1926; Boehner P., Bemerkungen zur Geschichte der Morganschen Gesetze in der Scholastik, "Arch. Philos.", 1951, No 4, S. 113–46.

Философская Энциклопедия. В 5-х т. — М.: Советская энциклопедия . Под редакцией Ф. В. Константинова . 1960—1970 .

Полезное

Смотреть что такое "ЗАКОНЫ ДЕ МОРГАНА" в других словарях:

Законы де Моргана — (правила де Моргана) логические правила, связывающие пары дуальных логических операторов при помощи логического отрицания. Открыты шотландским математиком Огастесом де Морганом Определение Огастес де Морган первоначально заметил, что в… … Википедия

Законы Моргана — * законы Моргана * Morgan’s Laws … Генетика. Энциклопедический словарь

Моргана законы — * Моргана законы * Morgan’s Laws or M. rules основные положения хромосомной теории наследственности, разработанные Т. Морганом и сотр. в 1911 1915 гг. Сводятся к следующему: 1) гены находятся в хромосомах и в пределах одной хромосомы образуют… … Генетика. Энциклопедический словарь

Моргана единица морганида М — Моргана единица, морганида, М * Моргана адзінка, марганіда, М * Morgan’s unit or M относительное расстояние между двумя генами на хромосоме, или частота рекомбинации () между двумя генетическими маркерами. Одна морганида соответствует 100%… … Генетика. Энциклопедический словарь

МОРГАНА ЗАКОНЫ — Предусматривают, что: гены находятся в хромосомах, и в пределах одной хромосомы образуют одну группу сцепления; гены в хромосомах расположены линейно; между гомологичными хромосомами в мейозе может происходить кроссинговер, частота которого пропо … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных

законы Моргана — Ряд закономерностей наследования, иногда объединяемых в общую группу З.М.: вхождение генов в хромосомы, представляющие собой группы сцепления, линейное расположение генов в хромосомах и наличие между гомологичными хромосомами мейотической… … Справочник технического переводчика

Законы Хаммурапи — Свод законов Хаммурапи (или Кодекс Хаммурапи), созданный приблизительно в 1780 г. до н. э., является одним из древнейших законодательных памятников. Найден археологической экспедицией Жака де Моргана в ходе раскопок в 1901 1902 годах в Сузах… … Википедия

Законы Хамураппи — Свод законов Хаммурапи (или Кодекс Хаммурапи), созданный приблизительно в 1780 г. до н. э., является одним из древнейших законодательных памятников. Найден археологической экспедицией Жака де Моргана в ходе раскопок в 1901 1902 годах в Сузах… … Википедия

Законы царя Хамураппи — Свод законов Хаммурапи (или Кодекс Хаммурапи), созданный приблизительно в 1780 г. до н. э., является одним из древнейших законодательных памятников. Найден археологической экспедицией Жака де Моргана в ходе раскопок в 1901 1902 годах в Сузах… … Википедия

законы Моргана — Morgan rules законы Моргана. Pяд закономерностей наследования, иногда объединяемых в общую группу З.М.: вхождение генов в хромосомы, представляющие собой группы сцепления, линейное расположение генов в хромосомах и наличие между гомологичными… … Молекулярная биология и генетика. Толковый словарь.

Лглаза Моргана это правила вывода, используемые в логике высказываний, которые устанавливают, что является результатом отрицания дизъюнкции и конъюнкции высказываний или переменных высказываний. Эти законы были определены математиком Августом Де Морганом..

Законы Моргана представляют собой очень полезный инструмент, чтобы продемонстрировать обоснованность математических рассуждений. Позже они были обобщены в рамках концепции множеств математиком Джорджем Булем.

Это обобщение, сделанное Булем, полностью эквивалентно начальным законам Моргана, но оно разработано специально для множеств, а не для предложений. Это обобщение также известно как законы Моргана.

1 Обзор логики высказываний
- 1.1 Ошибка
- 1.2 Предложения
- 2.1 Демонстрация
- 3.1 Объединение, пересечение и дополнение множеств
Обзор логики высказываний

Прежде чем посмотреть, какие конкретно законы Моргана и как они используются, удобно вспомнить некоторые базовые понятия логики высказываний. (Более подробно см. Статью по логике высказываний).

В области математической (или пропозициональной) логики логический вывод - это вывод, который выводится из ряда предпосылок или гипотез. Этот вывод вместе с упомянутыми предпосылками приводит к так называемым математическим рассуждениям.

Это рассуждение должно быть в состоянии быть продемонстрировано или опровергнуто; то есть, что не все выводы или выводы в математических рассуждениях являются действительными.

ошибочность

Ложный вывод, основанный на определенных предположениях, которые считаются истинными, называется ошибкой. Ошибки имеют особенность того, что аргументы кажутся правильными, но математически они не.

Логика высказываний отвечает за точную разработку и предоставление методов, с помощью которых можно без какой-либо двусмысленности подтвердить или опровергнуть математические рассуждения; то есть, сделать правильный вывод из помещения. Эти методы известны как правила вывода, частью которых являются законы Моргана..

предложения

Существенными элементами логики высказываний являются высказывания. Предложения - это утверждения, о которых можно сказать, являются ли они действительными или нет, но что они не могут быть истинными или ложными одновременно. Не должно быть никакой двусмысленности в этом вопросе.

Чтобы работать более широко, вместо рассмотрения конкретных предложений, мы рассматриваем пропозициональные переменные, которые представляют любые предложения и обычно обозначаются строчными буквами p, q, r, s и т. Д..

Пропозициональная формула - это комбинация пропозициональных переменных через некоторые из логических связок. Другими словами, это композиция пропозициональных переменных. Они обычно обозначаются греческими буквами.

Говорят, что пропозициональная формула логически подразумевает другую, когда последняя верна каждый раз, когда первая верна. Это обозначается как:

Когда логическая импликация между двумя пропозициональными формулами является взаимной, то есть когда предыдущая импликация действительна и в противоположном направлении, формулы называются логически эквивалентными, и они обозначаются как

Логическая эквивалентность является своего рода равенством между пропозициональными формулами и позволяет при необходимости заменять одно на другое..

Законы Моргана

Законы Моргана состоят из двух логических эквивалентностей между двумя пропозициональными формами, а именно:

Эти законы позволяют отделить отрицание дизъюнкции или конъюнкции как отрицание вовлеченных переменных.

Первое можно прочитать следующим образом: отрицание дизъюнкции равно соединению отрицаний. И второе звучит так: отрицание соединения - это дизъюнкция отрицания.

Другими словами, отрицать дизъюнкцию двух пропозициональных переменных эквивалентно соединению отрицаний обеих переменных. Аналогичным образом, отрицать конъюнкцию двух пропозициональных переменных равносильно дизъюнкции отрицаний обеих переменных.

Как упоминалось ранее, замена этой логической эквивалентности помогает продемонстрировать важные результаты, наряду с другими существующими правилами вывода. С их помощью вы можете упростить многие пропозициональные формулы, чтобы они были более полезными для работы.

Ниже приведен пример математического доказательства с использованием правил вывода, среди этих законов Моргана. В частности, показано, что формула:

Последнее проще понять и развить.

шоу

Стоит отметить, что законность законов Моргана может быть продемонстрирована математически. Одним из способов является сравнение ваших таблиц истинности.

наборы

Те же правила вывода и понятия логики, применяемые к высказываниям, также могут быть разработаны с учетом множеств. Это то, что известно как булева алгебра, после математика Джорджа Буля.

Чтобы дифференцировать случаи, необходимо изменить обозначения и перенести в множества все понятия, уже виденные в логике высказываний..

Набор представляет собой набор объектов. Наборы обозначаются заглавными буквами A, B, C, X, . а элементы набора обозначаются строчными буквами a, b, c, x и т. Д. Когда элемент a принадлежит множеству X, он обозначается как:

Когда он не принадлежит X, обозначение:

Способ представления наборов - размещение их элементов внутри ключей. Например, набор натуральных чисел представлен:

Например, набор целых чисел больше -4 может быть выражен как:

Или эквивалентно и более сокращенно, как:

Аналогично, следующие выражения представляют наборы четных и нечетных чисел соответственно:

Объединение, пересечение и дополнение множеств

Далее мы увидим аналоги логической связки в случае множеств, которые являются частью основных операций между множествами.

Союз и пересечение

Объединение и пересечение множеств определяются соответственно следующим образом:

Например, рассмотрим наборы:

Затем вы должны:

дополнение

Дополнение набора состоит из элементов, которые не принадлежат этому набору (того же типа, что и оригинал). Дополнение множества A обозначается как:

Например, в натуральных числах набор четных чисел является дополнением нечетных чисел, и наоборот.

Чтобы определить дополнение набора, необходимо с самого начала очистить универсальный или основной набор элементов, которые рассматриваются. Например, это не равно, чтобы рассмотреть дополнение набора на натуральных числах, что на рациональных.

В следующей таблице показано отношение или аналогия, которая существует между операциями над ранее определенными наборами и связующими из логики высказываний:

Законы Моргана для множеств

Наконец, законы Моргана о множествах таковы:

На словах: дополнение объединения - это пересечение дополнений, а дополнение пересечения - это объединение дополнений.

Лглаза Моргана это правила вывода, используемые в логике высказываний, которые устанавливают, что является результатом отрицания дизъюнкции и конъюнкции высказываний или переменных высказываний. Эти законы были определены математиком Августом Де Морганом..

Законы Моргана представляют собой очень полезный инструмент, чтобы продемонстрировать обоснованность математических рассуждений. Позже они были обобщены в рамках концепции множеств математиком Джорджем Булем.

Это обобщение, сделанное Булем, полностью эквивалентно начальным законам Моргана, но оно разработано специально для множеств, а не для предложений. Это обобщение также известно как законы Моргана.
- 1 Обзор логики высказываний
  - 1.1 Ошибка
  - 1.2 Предложения
  - 2.1 Демонстрация
  - 3.1 Объединение, пересечение и дополнение множеств
  Обзор логики высказываний
  
  Прежде чем посмотреть, какие конкретно законы Моргана и как они используются, удобно вспомнить некоторые базовые понятия логики высказываний. (Более подробно см. Статью по логике высказываний).
  
  В области математической (или пропозициональной) логики логический вывод - это вывод, который выводится из ряда предпосылок или гипотез. Этот вывод вместе с упомянутыми предпосылками приводит к так называемым математическим рассуждениям.
  
  Это рассуждение должно быть в состоянии быть продемонстрировано или опровергнуто; то есть, что не все выводы или выводы в математических рассуждениях являются действительными.
  
  ошибочность
  
  Ложный вывод, основанный на определенных предположениях, которые считаются истинными, называется ошибкой. Ошибки имеют особенность того, что аргументы кажутся правильными, но математически они не.
  
  Логика высказываний отвечает за точную разработку и предоставление методов, с помощью которых можно без какой-либо двусмысленности подтвердить или опровергнуть математические рассуждения; то есть, сделать правильный вывод из помещения. Эти методы известны как правила вывода, частью которых являются законы Моргана..
  
  предложения
  
  Существенными элементами логики высказываний являются высказывания. Предложения - это утверждения, о которых можно сказать, являются ли они действительными или нет, но что они не могут быть истинными или ложными одновременно. Не должно быть никакой двусмысленности в этом вопросе.
  
  Чтобы работать более широко, вместо рассмотрения конкретных предложений, мы рассматриваем пропозициональные переменные, которые представляют любые предложения и обычно обозначаются строчными буквами p, q, r, s и т. Д..
  
  Пропозициональная формула - это комбинация пропозициональных переменных через некоторые из логических связок. Другими словами, это композиция пропозициональных переменных. Они обычно обозначаются греческими буквами.
  
  Говорят, что пропозициональная формула логически подразумевает другую, когда последняя верна каждый раз, когда первая верна. Это обозначается как:
  
  Когда логическая импликация между двумя пропозициональными формулами является взаимной, то есть когда предыдущая импликация действительна и в противоположном направлении, формулы называются логически эквивалентными, и они обозначаются как
  
  Логическая эквивалентность является своего рода равенством между пропозициональными формулами и позволяет при необходимости заменять одно на другое..
  
  Законы Моргана
  
  Законы Моргана состоят из двух логических эквивалентностей между двумя пропозициональными формами, а именно:
  
  Эти законы позволяют отделить отрицание дизъюнкции или конъюнкции как отрицание вовлеченных переменных.
  
  Первое можно прочитать следующим образом: отрицание дизъюнкции равно соединению отрицаний. И второе звучит так: отрицание соединения - это дизъюнкция отрицания.
  
  Другими словами, отрицать дизъюнкцию двух пропозициональных переменных эквивалентно соединению отрицаний обеих переменных. Аналогичным образом, отрицать конъюнкцию двух пропозициональных переменных равносильно дизъюнкции отрицаний обеих переменных.
  
  Как упоминалось ранее, замена этой логической эквивалентности помогает продемонстрировать важные результаты, наряду с другими существующими правилами вывода. С их помощью вы можете упростить многие пропозициональные формулы, чтобы они были более полезными для работы.
  
  Ниже приведен пример математического доказательства с использованием правил вывода, среди этих законов Моргана. В частности, показано, что формула:
  
  Последнее проще понять и развить.
  
  шоу
  
  Стоит отметить, что законность законов Моргана может быть продемонстрирована математически. Одним из способов является сравнение ваших таблиц истинности.
  
  наборы
  
  Те же правила вывода и понятия логики, применяемые к высказываниям, также могут быть разработаны с учетом множеств. Это то, что известно как булева алгебра, после математика Джорджа Буля.
  
  Чтобы дифференцировать случаи, необходимо изменить обозначения и перенести в множества все понятия, уже виденные в логике высказываний..
  
  Набор представляет собой набор объектов. Наборы обозначаются заглавными буквами A, B, C, X, . а элементы набора обозначаются строчными буквами a, b, c, x и т. Д. Когда элемент a принадлежит множеству X, он обозначается как:
  
  Когда он не принадлежит X, обозначение:
  
  Способ представления наборов - размещение их элементов внутри ключей. Например, набор натуральных чисел представлен:
  
  Например, набор целых чисел больше -4 может быть выражен как:
  
  Или эквивалентно и более сокращенно, как:
  
  Аналогично, следующие выражения представляют наборы четных и нечетных чисел соответственно:
  
  Объединение, пересечение и дополнение множеств
  
  Далее мы увидим аналоги логической связки в случае множеств, которые являются частью основных операций между множествами.
  
  Союз и пересечение
  
  Объединение и пересечение множеств определяются соответственно следующим образом:
  
  Например, рассмотрим наборы:
  
  Затем вы должны:
  
  дополнение
  
  Дополнение набора состоит из элементов, которые не принадлежат этому набору (того же типа, что и оригинал). Дополнение множества A обозначается как:
  
  Например, в натуральных числах набор четных чисел является дополнением нечетных чисел, и наоборот.
  
  Чтобы определить дополнение набора, необходимо с самого начала очистить универсальный или основной набор элементов, которые рассматриваются. Например, это не равно, чтобы рассмотреть дополнение набора на натуральных числах, что на рациональных.
  
  В следующей таблице показано отношение или аналогия, которая существует между операциями над ранее определенными наборами и связующими из логики высказываний:
  
  Законы Моргана для множеств
  
  Наконец, законы Моргана о множествах таковы:
  
  На словах: дополнение объединения - это пересечение дополнений, а дополнение пересечения - это объединение дополнений.
  
  Читайте также: