Закон био савара лапласа кратко

Обновлено: 06.07.2024

Закон Био́ — Савáра — Лапла́са (также Закон Био́ — Савáра) — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Установлен экспериментально Био и Саваром и сформулирован в общем виде Лапласом.

Роль закона Био — Савара — Лапласа в магнитостатике аналогична роли закона Кулона в электростатике. Он широко используется для расчёта магнитного поля по заданному распределению токов.

В современной методологиии закон Био — Савара — Лапласа, как правило, рассматривается как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля.

Одним из величайших достижений науки о природе 19 века является доказательство непосредственной связи между электрическим и магнитным полем. Считается, что полным описанием их взаимодействия являются уравнения Максвелла. Закон Жана-Батиста Био и Феликса Савара можно рассматривать как одно из их следствий, но он был открыт намного раньше.

История открытия закона

Электрическое и магнитное поле сначала рассматривали отдельно. Экспериментально установил факт порождения электрическим током магнитного поля датский учёный Ханс Кристиан Эрстед в 1820 году. Публичная демонстрация этого эффекта показала, что под воздействием электрического тока происходит отклонение магнитной стрелки. Открытия Эрстеда послужили основанием для исследований, проводимых Био и Саваром. Последние постарались выявить математические закономерности рассматриваемой зависимости.

Жан-Батист Био был профессором физики в Сорбонне. Узнав о достижениях Эрстеда, он с помощью коллеги Феликса Савара стал проверять воздействие проводников на различные разновидности магнитных стрелок. В итоге была найдена математически выраженная закономерность зависимости.

Формулировка закона

При описании эффектов необходимо разбить проводник, через который проходит ток, на элементарные участки, имеющие минимальную длину. Каждый из них создаёт магнитное поле. Воздействие всех участков необходимо просуммировать, чтобы узнать силу воздействия поля в конкретной точке. Это правило называется принципом суперпозиции.

Закон утверждает, что магнитное поле прямо пропорционально длине прямолинейного участка провода и силе тока, а также обратно пропорционально расстоянию до рассматриваемой точки. Оно направлено перпендикулярно электрическому току и направлению от проводника к точке измерения.

Направленность поля можно определить по правилу правой руки. Если указательный палец направлен также как сила тока, средний палец направлен на точку, где определяется магнитное поле, то большой палец, поставленный перпендикулярно к указательному и среднему, показывает направление магнитного поля.

Формула, связывающая эти величины, представлена на рисунке ниже.

Чтобы определить, какое магнитное поле создаёт весь проводник, проводится суммирование влияния каждого участка. В отдельных случаях могут быть получены относительно простые формулы, в других для получения результата нужно разбираться в методах дифференциального и интегрального исчисления.

В качестве примера можно привести формулу для кругового тока.

Для прямого тока эта формула будет выражена следующим образом:

При вычислениях надо помнить, что dl, dB и B являются векторными величинами. В первом случае величина элемента тока равна длине участка, а направление совпадает с тем, которое имеет проходящий по нему ток. Направление dB определяется по правилу правой руки, а величина — по приведённой формуле. B представляет векторную сумму всех имеющихся dB.

Закон Био-Савара и уравнения Максвелла

Экспериментально подтвержденный закон в формулировке Био-Савара был важным этапом в познании электромагнитных полей. В частности, на их основе Максвелл разработал свои уравнения, описывающие такие поля. Впоследствии была сделана математическая формулировка закона на основании этих уравнений.

Однако надо отметить, что вычисления Максвелла более сложные по сравнению с тем, как их трактует закон о магнитном поле Био-Савара. Формулировка Максвелла с учётом того, что электрическое поле постоянно, выглядит таким образом:

Эта формула может быть применена к контуру произвольной сложности. Если сила тока I является постоянной величиной, то его можно вынести за знак интеграла. В формуле использованы знаки умножения в смысле векторной операции. Если в качестве точки отсчёта будет использована точка, где происходит определение напряжённости электромагнитного поля, то формула может быть упрощена и будет выглядеть таким образом.

Особенности вычислений

При рассмотрении закона Био-Савара речь идёт о бесконечно малых проводниках. Точную их длину указать нельзя. Известно только то, что она настолько мала, что участок можно считать прямолинейным.

Ещё одно предположение состоит в том, что речь идёт об очень тонких проводах. Это означает, что их толщина пренебрежимо мала по сравнению с расстоянием от точки измерения.

Фактически вычисления основаны на том, что для малых и тонких проводников задача относительно простая, но если сложить их влияние, то будет получена точная величина магнитного поля в нужной точке.

В приведённых рассуждениях предполагалось, что для простых случаев линии напряжённости являются концентрическими окружностями. Если среда неоднородная, то магнитная проницаемость в различных точках может отличаться, что сделает форму силовых линий более сложной.

Закон в формулировке Био-Савара позволяет определить характеристики магнитного поля постоянного тока для практически любой конфигурации контура. Этот закон также носит имя Лапласа.

Био и Савар предприняли тщательные экспериментальные исследования рассматриваемого вопроса и предложили формулу для вычисления в некоторых относительно простых случаях. Лаплас обобщил полученные результаты. Он предложил использовать принцип суперпозиции и бесконечно малые участки провода для описания свойств сложных контуров. Фактически закон является плодом усилий этих трёх известных учёных, поэтому его полное название — закон Био-Савара-Лапласа.

При этом нужно учитывать, что Лаплас фактически был одним из создателей дифференциального и интегрального исчисления, принципы которого он использовал для углублённого изучения рассматриваемого закона.

Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.

Содержание

Формулировка

Пусть постоянный ток течёт по контуру γ , находящемуся в вакууме, _0" width="" height="" />
— точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)

Направление перпендикулярно и , то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)

Векторный потенциал даётся интегралом (в системе СИ)

Вывод из уравнений Максвелла

Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системе СГС)

\,\mathbf B = \frac<4\pi> \mathbf j" width="" height="" />
\,\mathbf B = 0" width="" height="" />
\,\mathbf E = 0" width="" height="" />
\,\mathbf E = 4\pi \rho" width="" height="" />

где — плотность тока в пространстве. При этом электрическое и магнитное поля оказываются независимыми. Воспользуемся векторным потенциалом для магнитного поля (в системе СГС):

Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:

Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:

Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:

Тогда магнитное поле определяется интегралом (в системе СГС)

аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что

Французские ученые Ж. Био и Ф. Савар в 1820 -м году проводили эксперименты над магнитным полем постоянных токов. Физики доказали, что индукция магнитного поля проходящих по проводнику токов зависит от совместного действия всех участков данного проводника. Работа магнитного поля основана на принципе суперпозиции.

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

Индукция B → проводника с током представлена, как векторная сумма элементарных индукций ∆ B → вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Закон Био–Савара

Закон Био-Савара определил вклад ∆ B → в магнитную индукцию B → результативного магнитного поля, образуемый маленьким участком Δ l проводника с током I .

∆ B = μ 0 · I · ∆ l · sin α 4 π r 2 .

В формуле r – это расстояние от заданного участка Δ l до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ 0 – это магнитная постоянная.

Используя правило буравчика, определим направление вектора ∆ B → : оно указывает на ту сторону, в которую вращается рукоятка буравчика при его поступательном движении вдоль тока. Рисунок 1 . 17 . 1 наглядно показывает закон Био-Савара с применением магнитного поля прямолинейного проводника с током. Если сложить (интегрировать) вклады в магнитное поле всех участков проводника с током, тогда получим формулу для магнитной индукции поля прямого тока:

Рисунок 1 . 17 . 1 . Иллюстрация закона Био–Савара.

С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

где R – это радиус кругового проводника.

Чтобы определить направление вектора B → тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

Объясним, что означает циркуляция вектора B → . Допустим, в пространстве с магнитным полем существует какой-то условный замкнутый контур, а также положительное направление его обхода. Тогда, на каждом отдельном маленьком участке Δ l данного контура определяется касательная составляющая B l вектора B → в этом месте, то есть определяется проекция вектора B → на направление касательной к заданному участку контура. Рисунок 1 . 17 . 2 наглядно демонстрирует это.

Рисунок 1 . 17 . 2 . Замкнутый контур ( L ) с заданным направлением обхода. Изображение токов I 1 , I 2 и
I 3 , создающих магнитное поле.

Циркуляция вектора B → – это сумма произведений B l ∆ l , взятая по целому контуру L : B → = ∑ ( L ) B l ∆ l.

Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Согласно теореме о циркуляции, циркуляция вектора B → магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ 0 на сумму всех токов:

∑ ( L ) B l ∆ l = μ 0 ∑ l i.

На рисунке 1 . 17 . 2 продемонстрирован пример с несколькими проводниками с токами, образующими магнитное поле. Ток I 2 и ток I 3 пронзают контур L в противоположных направлениях, им приписываются различные знаки. Положительным является ток, который связан с заданным направлением обхода контура по правилу буравчика.

Значит, I 3 > 0 , а I 2 0 . Ток I 1 не пронзает контур L .

Теорема о циркуляции в этом примере математически выражается следующей формулой:

∑ ( L ) B l ∆ l = μ 0 ( I 3 - I 2 ) .

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

Самый простой пример использования теоремы о циркуляции – это вывод формулы магнитного поля прямолинейного проводника с током. С учетом симметрии в этой задаче контуром L лучше выбрать окружность какого-то радиуса R , лежащую в перпендикулярной проводнику плоскости. Центр окружности задан в какой-то точке проводника. Из-за симметрии вектор B → направляется по касательной ( B l = B ) , а его модуль имеет одинаковое значение по всей окружности. Использование теоремы о циркуляции приводит к выражению:

∑ ( L ) B l ∆ l = 2 π R B = μ 0 I ,

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B → можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

Рассмотрим одну из них – это задачу расчета поля тороидальной катушки (рисунок 1 . 17 . 3 ).

Рисунок 1 . 17 . 3 . Использование теоремы о циркуляции к тороидальной катушке.

Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Одна линия индукции какого-то радиуса r 1 ≤ r r 2 представлена на рисунке 1 . 17 . 3 . Используем теорему о циркуляции для контура L в виде окружности, которая совпадает с линией индукции магнитного поля, изображенной на рисунке 1 . 17 . 3 . Опираясь на соображения о симметрии, делаем вывод, что модуль вектора B → имеет одинаковое значение по всей линии. Исходя из теоремы о циркуляции, запишем:

B · 2 π r = μ 0 I N ,

где N – это полное количество витков, а I – это ток, протекающий по виткам катушки. Значит, B = μ 0 I N 2 π r .

Так, модуль вектора магнитной индукции в тороидальной катушке находится в зависимости от радиуса r . При условии, что сердечник катушки тонкий, то есть r 2 – r 1 ≪ r , тогда магнитное поле внутри катушки почти однородное.

Величина n = N 2 π r – это количество витков на единицу длины катушки. Следовательно, B = μ 0 I n .

Сюда не относится радиус тора, потому оно действует и в предельном случае r → ∞ .

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

На рисунке 1 . 17 . 4 представлено магнитное поле катушки конечной длины. Обращаем внимание, что в центре катушки магнитное поле почти однородное и намного сильнее, чем снаружи. Это объясняется густотой линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью находится внутри него.

Рисунок 1 . 17 . 4 . Магнитное поле катушки конечной длины. В центральной части соленоида магнитное поле почти однородное и существенно больше по модулю поля вне катушки.

В случае с бесконечно длинным соленоидом соотношение для модуля магнитной индукции получаем прямо из теоремы о циркуляции, применяя ее к прямоугольному контуру, изображенному на рисунке 1 . 17 . 5 .

Рисунок 1 . 17 . 5 . Теорема о циркуляции при расчете магнитного поля бесконечно длинного соленоида.

Проекция вектора магнитной индукции на направление обхода контура a b c d только на стороне a b отлична от 0 . Значит, циркуляция вектора B → по контуру равняется B l , где l – это длина стороны a b . Количество витков соленоида, пронзающих контур a b c d , равняется n · l , где n – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется I n l . Из теоремы о циркуляции, B l = μ 0 I n l .

Отсюда B = μ 0 I n .

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

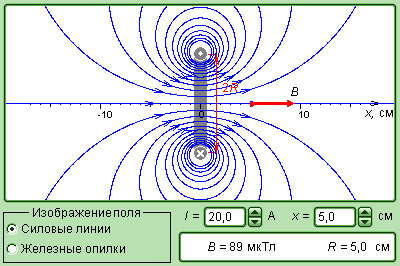
Рисунок 1 . 17 . 6 . Модель магнитного поля кругового витка с током.

Читайте также:

  
• Приведите примеры демонстрирующие различные свойства информации кратко
  
• Экологические группы почвенных организмов кратко
  
• Методика изучения площадей в школьном курсе планиметрии
  
• Образец договора об оказании платных образовательных услуг в школе в ворде
  
• Деловые качества педагога для аттестации в доу