Задача в математике это кратко
Обновлено: 02.07.2024
| Вложение | Размер |
|---|---|
| statya_zadacha.doc | 47.5 КБ |
Предварительный просмотр:
Задача – это проблемная ситуация с явно заданной целью, которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать [Тихомиров О. К.].
Вопрос. Состоит из вопросительного слова и объекта поиска (иногда в вопросе можно обнаружить часть условия). Каждое вопросительное слово имеет своё значение и задаёт направление поиска. Например: куда ? – указывает на время, где ? – на место, сколько ? – на количество, почему ? – на причину.
Теория. Состоит из понятий, между которыми построены причинно-следственные связи. Конкретные объекты отсутствуют. Каждому учителю надо помнить о значении теории, т.к. без неё невозможно решить ни одной задачи.
Выбор правильной теории – огромное дело при разборе (анализе) задачи, но этого недостаточно, потому что теория может быть очень объёмной, содержать множество блоков, но не все они нужны для решения задачи. Помогает выбрать нужный блок схема типа представленной ниже.
Особое внимание необходимо уделять урокам обобщения изученного материала, на которых совместно с учениками полезно строить причинно-следственные связи между понятиями, создавать теорию и в дальнейшем применять её при решении задач.
Доктор Айболит обезьянке Чичи дал 3 ложки микстуры, а собаке Авве – 4 ложки. Всего он дал больным 7 ложек микстуры.
Доктор Айболит обезьянке Чичи дал 3 ложки микстуры, а собаке Авве – 4 ложки. Сколько ложек Микстуры ушло на лечение обеих больных?
- Сравни тексты. Чем эти тексты похожи? Чем отличаются?
- Какой текст вы считаете задачей? Почему?
- Какое действие поможет ответить на вопрос задания?
- Что тебе подсказало действие для решения задачи?
- Ты знаешь, каким действием нужно решить эту задачу?
- Раздели задачу на 2 части.
- Сделай к задаче рисунок и реши её.
- Придумай и запиши задачу другую задачу к тому же рисунку.
- Найди и прочитай ту часть задачи, которая рассказывает, что в ней известно.
- Прочти вторую часть задачи, о чём она тебе сообщила?
- Прочитай текст и докажи что это задача.
- Назови данные числа. В какой части задачи ты их отыскал?
Очень полезно показывать учащимся, как создаются задачи, т. к. этот процесс способствует осознанному представлению о структуре задачи, а также развитию математических способностей и мышления младших школьников.
При работе над составлением задач можно использовать следующие задания:
- Задачи с отсутствующим вопросом . В этих задачах не формулируется вопрос, но этот вопрос логически вытекает из данных в задаче математических отношений. Задача решается после того, как сформулирруется вопрос (иногда в задаче можно поставить несколько вопросов).
Например, На протяжении 155 м уложено 25 труб длиной 5 м и 8 м. (Сколько уложено тех и других труб?)
2) Задачи с недостающими данными . В задачах этого типа отсутствуют некоторые данные, вследствие чего дать точный ответ на вопрос задачи не представляется возможным. Школьник должен проанализировать задачу и доказать, почему нельзя дать точного ответа на вопрос задачи, чего не хватает, что нужно добавить.
Например, Банка с мёдом весит 500 г. Такая же банка с керосином – 350 г. Сколько весит пустая банка? (нужно знать отношение веса мёда и керосина.)
3) Задачи с излишними данными . В эти задачи введены ненужные данные. Ученики должны выделить те данные, которые необходимы, для решения, и указать на лишние, ненужные.
Например, Четыре гири разного веса весят вместе 40 кг. Определите вес самой тяжёлой гири, если известно, что каждая из них втрое тяжелее другой, более лёгкой, и что самая лёгкая весит в 12 раз меньше, чем весят вместе две средних.
4) Составление задач с теми же числовыми данными . Поменяйте сюжет задачи, оставляя при этом те же числа.
5) Составление задач с тем же сюжетом, но другими числовыми данными.
6) Составление задач, обратных данной .
3. Тихомиров О. К. Психология мышления. М., 1984.
По теме: методические разработки, презентации и конспекты

Данная статья поможет решить Проблему: Как формировать положительную мотивацию у младших школьников на уроках литературного чтения? Какие методы и приемы эффективны для получения положитель.
выступление на МО "Стандартные задачи в начальном курсе математики"
презентация, выступление на МО.

статья по теме "Формирование элементарных этических понятий у обучающихся начальных классов через внеурочную деятельность"
Данная статья посвящена проблеме духовно-нравственного воспитания обучающихся начальных классов в коррекционной школе 8 вида.

Статья на тему "Формирование универсальных учебных действий учащихся начальной школы"
В статье раскрывается актуальность данной темы, даётся классификация УУД, не примере различных учебных дисциплин доказывается возможность формирования различных УУД.

Данная статья раскрывает возмжности УМК "Начальная школа 21 века" в формировании универсальных учебных действий на уроках математики.
Статья на тему: "Формирование навыков техники чтения в начальных классах"
Лучшие упражнения для тренировки техники чтенияОптимальная скорость чтения должна соответствовать темпу разговорной речи — 120 – 150 слов в минуту. Чтобы добиться таких результатов необход.
В рамках математической науки задачи соседствуют с понятиями и определениями, алгоритмами, теоремами и т.д. При этом задачи занимают особое место, так как все теоретические знания усваиваются посредством решения задач.
Очевидно, что задачи являются одним из главных компонентов содержания учебного предмета математики. По этой причине нужно с особым вниманием подойти к определению понятия задачи.
Понимание задачи как определённой системы обнаруживается в работах Г.А.Балл, Ю.М.Колягина, Л.М.Фридмана, А.Ф.Эсаулова и др. Г.А.Балл определяет задачу как «систему, обязательными компонентами которой являются:
а) предмет задачи, находящийся в исходном состоянии;
б) модель требуемого состояния предмета задачи (эту модель мы отождествляем с требованием задачи).
Структура задачи
Учитывая разнообразие трактовок, можно обозначить структурные элементы задачи как объекта мыслительной деятельности:
- Условие (У) - предметная область задачи (объекты) и отношения между объектами.
- Обоснование (О) - теоретические или практические основания для перехода от условия к заключению посредством операций, которые составляют решение задачи, т.е. базис задачи.
- Решение (Р) – совокупность действий или операций, которую необходимо произвести над известными компонентами, чтобы выполнить требование, сформулированное в заключении,– оператор задачи.
- Заключение (З) - требование отыскать неизвестные компоненты, убедиться в правильности чего-либо, доказать, сконструировать и т.д.
- решение задачи как план (способ, метод) осуществления требования задачи;
- решение задачи как процесс выполнения плана, требования задачи;
- решение задачи как результат выполнения плана решения задачи.
Классификации задач
Процесс решения задач зависит от ряда субъективных факторов. Так, Ю.М.Колягин классифицировал задачи по признаку проблемности:
Стандартные задачи: решающему известны все компоненты задачи (условие (У); обоснование (О); решение (Р); заключение (З). Именно такие задачи реализуются на этапе усвоения теоретического материала. Данный тип задач позволяет не только закрепить полученные теоретическое знания, но и проверить уровень понимания, осуществить обратную связь. Так, на этапе усвоения теоретического материала после введения теории (определения, понятия, правила) учитель может использовать задачи на распознавание: относится тот или иной объект к введенному понятию.
Обучающие задачи: один компонент неизвестен – х. Тогда задача схематично может выглядеть так: УОРх, УОхЗ, УхРЗ, хОРЗ.
Рассмотрим примеры задач данного типа:
Дано: 2х 2 + х 2 – 5 = 0. Используя формулу нахождения квадратных корней, найдите х.
Витя нашёл корни квадратного уравнения, применив теорему, обратную теореме Виета. Объясните, как он это сделал.
Маша определила корни квадратного уравнения, разложив его на множители. Назовите математический факт, положенный в основу такого уравнения.
Задача 4. (хОРЗ) Корни квадратного уравнения равны 1 и -1. Они получены с использованием формулы разности квадратов. Составьте соответствующее корням квадратное уравнение.
Поисковые задачи: неизвестны два компонента х и у. Тогда задача схематично выглядит так: УхуЗ, УОху, хуРЗ, УхРу, хОуЗ.
Рассмотрим примеры задач данного типа:
Света изучает математику в кружке. Среди школьников в этом кружке 94% процента мальчиков. Установите наименьшее возможное количество учеников в кружке.
Проблемные задачи: неизвестны три компонента х, у, z. Тогда задача схематично выглядит так: Ухуz, xОуz, хуРz, xyzЗ.
Рассмотрим примеры задач данного типа:
Корабли находятся в открытом море в точках А и В. Расстояние между точками – 50 км. Корабли одновременно начинают движение друг к другу прямолинейно в независимых направлениях со скоростями соответственно 15 км/ч и 20 км/ч. Найдите наибольшее возможное время движения кораблей до момента их встречи в точке С.
От структуры задачи зависит тип деятельности, необходимой для решения задачи:
- репродуктивная или алгоритмическая деятельность (воспроизведение способа решения);
- продуктивная деятельность (использование известного способа решения в изменившихся условиях, привлечение знаний из других тем);
- эвристическая деятельность (поиск решения творческим путём).
- По математическому содержанию.
В зависимости от того, какому разделу арифметики компоненты У и З, задачи бывают:
- арифметические,
- алгебраические,
- геометрические,
- тригонометрические и т.д.
- По методу решения.
В зависимости от того, каким образом представлены компоненты О и Р задачи классифицируют на:
- арифметические, в основе которых лежит зависимость между компонентами арифметических действий.
- алгебраические, задачи, в которых требуется составление уравнений,
- геометрические, задачи, в которых необходимо выполнить построение геометрических фигур, охарактеризовать их свойства,
- комбинированные задачи;
- По характеру требований.
Классификация задач основана на представлении в задачи компонента З:
- задачи на объяснение,
- задачи на вычисление,
- задачи на доказательство,
- задачи на построение и т.д.
- По специфике языка:
- текстовые, где условие представлено на естественном языке,
- сюжетные (задачи, в которых присутствует фабула),
- абстрактные – к ним относятся предметные задачи.
Образовательный процесс испытывает на себе влияние со стороны окружающего мира. Так, в информационную эпоху наиболее целесообразным становится образный способ представления информации и комбинация разных способов кодирования. Школьный курс математики преимущество отдается трем способам кодирования:
- словесный,
- символьный,
- образный (таблицы, графики, схемы, чертежи, рисунки).
Образный способ можно разделить на подтипы в зависимости от используемых условных обозначений: образно-графический (требуется чтение и понимание легенды) и образно-иконический (нет необходимости читать легенду). Оба способа предполагают сформированность таких умений, как воспринимать условные обозначения, устанавливать связи между ними и самими объектами.
Следовательно, можно классифицировать задачи с опорой на наличие/отсутствие требования перекодировки информации (т.е. изменить способ представления информации, который использовался в задаче изначально); способ представления задачи одним или несколькими способом кодирования информации.
Таким образом, получим следующую классификацию математических задач по способам кодирования информации:
- Задачи, не требующие перекодировки.
- Задачи, требующие перекодировки.
К задачам, не требующим перекодировки (первый тип) можно отнести:
- задачи, представленные с использованием одного способа кодирования (первый тип задач);
- задачи, в которых используется несколько способов кодирования (второй тип задач).
К задачам, требующим перекодировки (третий тип) относятся задачи, в которых требуется изменить способ кодирования, представленный в задаче изначально, а именно:
- задачи на внутриобразные перекодировки;
- задачи на символьно-словесные перекодировки;
- задачи на словесно-образные перекодировки;
- задачи на образно-символьные перекодировки.
- задачи на сложные перекодировки.
Задачи, представленные с использованием преимущественно одного способа кодирования информации (образного, символьного или словесного) требуют решения этим же способом. Следует помнить, что не существует задач, представленных исключительно с использованием образного кодирования: всегда требуется словесный комментарий. При этом решение задачи может быть полностью образным. К тому же, задачи, сформулированные словесно, содержат в себе символы (числа).
Задачи второго типа (задачи, в которых используется несколько способов кодирования) требуют от учащегося умения ориентироваться в разных способах представления информации. Данные задачи не требуют от учащегося перекодировки информации из одного способа в другой, его задача - сориентироваться в данном способе кодирования и представления информации, и найти решение. К задачам такого типа можно отнести задачи на выбор правильного ответа, задачи нас соответствие, при этом условия могут быть представлены разным способом кодирования.
Задачи третьего типа (задачи, требующие перекодировки) в обязательном порядке предполагают перекодировку информации. Решая задачу такого типа, учащийся перекодирует информацию, представляя ее отличным от условия способом. Сложная перекодировка сочетает в себе несколько перекодировок.
Рассмотрим пример задачи второго типа: задачи, в которых используется несколько способов кодирования.
Формы представления информации: словесная и образно-иконическая Данная задача предполагает ее перевод в графическую форму.
Стадион имеет форму круга с диаметром d. Точка 0 является стартом и финишем. Спортсмен пробегает по окружности стадиона один круг. Изобразите схематически зависимость расстояния между стартом и положением спортсмена (R) от длины пути, который пробежал спортсмен (l).
Рассмотрим пример задачи третьего типа: задача на сложную перекодировку.
Функции 1–6 заданы разными способами. Установите соответствие между функциями (1-6) и промежутками их возрастания (а–д).
Функции
Промежутки
числа натурального ряда меньше пяти
(1; 2) U (2; 3) U (3; 4)
у(х)=-(х+1) 2 , где х ∈ [1;4]
множество х: 1 ≤ х ≤ 4
Классификация задач по любому из вышеуказанных признаков остаётся достаточно условной. Во-первых, способы решения не исключают друг друга, во-вторых, одна и та же задача может быть представлена разными способами, в-третьих, степень проблемности зачастую зависит не от самой задачи, а от того, кто её решает. Тем не менее, различные типологии помогают учителю ориентироваться в многообразии материала.
В рамках школьного курса математики немаловажную роль играют сюжетные задачи. Именно при помощи сюжетных задач осуществляется обучение школьников методу моделирования. Моделирование предполагает описание реальных процессов на языке математики и лежит в основе курса.
Помимо вышеизложенных типологий к этому типу задач можно применить типологизацию с опорой на сюжет (покупки, движение, работа механизма и др.). Наиболее высоким уровнем проблемности обладают сюжетные задачи образного типа. Их также можно отнести к эвристическим. Для решения такой задачи требуется целостное восприятие задачи с опорой на заданный образ. Сложность заключается именно в субъективном восприятии образа, что и затрудняет поиск способа решения.
Приведем пример сюжетной задачи:
В русском лесу 10 колодцев. В колодцах мертвая-живая вода. Выпьешь такой воды – умрёшь, если не успеешь запить водой из колодца с большим номером. Колодцами 1–9 владеет Иван-Царевич, колодец 10 принадлежит Кощею. Между ними должен состояться поединок, суть которого в том, чтобы предложить противнику стакан воды. При этом нельзя использовать воду из колодца противника. Придумайте, как Ивану-Царевичу остаться в живых, после того как его угостит Кощей? Как Иван-Царевич может погубить Кощея, дав ему стакан воды?
В рамках школьного курса математики применение задач опирается на логику формирования теоретической базы, при этом учитывается сложность самих задач. Под сложностью понимается объективная характеристика задачи, которая зависит от:
- формулировки задания (с использованием естественного или искусственного языка, терминов и понятий из разных предметных областей);
- логическая и грамматическая структура текста (проще воспринимается та задача, в которой условие предваряет заключение, нежели та, в которой заключение предшествует или разрывает условие);
- количества и характера связей.
При решении задачи большое значение имеет субъективный компонент. В связи с этим вступает в силу критерий трудности задачи.
Трудность – характеристика задачи, которая находится в зависимости от субъектного опыта решающего (математические знания, знания из других предметных областей, учебные умения, качества мышления, бытовой опыт).
Приведем пример задачи данного типа:

- Что известно в задаче? На языке математики это называется условием задачи.
- Что нужно узнать? Это вопрос задачи. Без вопроса нет задачи.
Почти к каждой задаче можно записать схему, то есть ее краткую запись.
- Сосчитайте, сколько птичек стало? Это решение задачи.
К каждой задаче нужно записать ответ.
Составные части задачи

.
К празднику в детский сад купили 7 маленьких воздушных шариков, а больших - на 2 меньше.
Любое математическое задание можно рассматривать как задачу, выделив в нем условие, т. е. ту часть, где содержатся сведения об известных и неизвестных значениях величин, об отношениях между ними, и требование (т. е. указание на то, что нужно найти). Рассмотрим примеры математических заданий из курса начальных классов:
• Поставь знаки , =, чтобы получились верные записи: 3 . 5, 8 . 4.
Условие задачи - числа 3 и 5, 8 и 4. Требование - сравнить эти числа.
Реши уравнение: х + 4 = 9.
В условии дано уравнение. Требование - решить его, т. е. подставить вместо х такое число, чтобы получилось истинное равенство.
• Выбери из данных фигур те, из которых можно сложить прямоугольник.
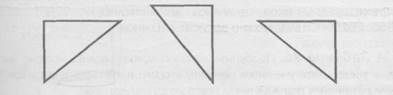
Здесь в условии даны треугольники. Требование - сложить прямоугольник.
Для выполнения каждого требования применяется определенный метод или способ действия, в зависимости от которого выделяют различные виды математических задач: на построение, доказательство, преобразование, комбинаторные задачи, арифметические и т. д.
При обучении младших 'школьников математике решению этих задач уделяется большое внимание. Это обусловлено следующим,
1. В сюжетах находят отражение практические ситуации, имеющие место в жизни ребенка. Это помогает ему осознать реальные количественные отношения между различными объектами (величинами) и тем самым углубить и расширить свои представления о реальной действительности.
2. Решение этих задач позволяет ребенку осознать практическую значимость тех математических понятий, которыми он овладевает в начальном курсе математики.
3. В процессе их решения у ребенка можно формировать умения, необходимые для решения любой математической задачи (выделять данные и искомое, условие и вопрос, устанавливать зависимость между ними, строить умозаключения, моделировать, проверять полученный результат).
Рассмотрим различные способы решения текстовых задач на конкретном примере:
• Задача. Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т. д., пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ решения можно назвать практическим или предметным. Его возможности ограничены, так как учащиеся могут выполнить предметные действия только с небольшими количествами. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практически, а арифметическим способом, записав равенство: 8:2 = 4
Для решения можно применить алгебраический способ, рассуждая при этом так: «Число тарелок неизвестно, обозначим их буквой х. На каждой тарелке 2 яблока, значит, число всех яблок - это '2-х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2-х=8 и решить его: х = 8:2, х = 4.
Ту же задачу можно решить графическим способом, изобразив каждое яблоко отрезком. Этот способ решения близок к практическому, но носит более абстрактный характер и требует специального разъяснения.


Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называют простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называют составными. Составную задачу, так же как и простую, можно решить, используя различные способы. Например:
• Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные - щуки. Сколько щук поймал рыбак?
Практический способ.
 |
| Для ответа на вопрос задачи можно не выполнять арифметические действия, т. к. количество пойманных щук соответствует тем «ругам, которые не обозначены (их 3). |
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим пойманных рыб: л - лещи, о - окуни.
Арифметический способ.
1) 3 + 4 = 7 (р.) - пойманные рыбы;
2) 10 - 7 = 3 (р.) - щуки.
Для ответа на вопрос задачи мы выполнили два действия.
Алгебраический способ.
Пусть х - пойманные щуки. Тогда количество всех рыб можно записать выражением:
3 + 4 + х~ все рыбы.
По условию задачи известно, что рыбак поймал всего 10 рыб. Значит: 3 + 4 + х= 10.
Решив это уравнение, мы ответим на вопрос задачи.
Графический способ.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
|/ Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.
/ В начальных классах используются различные формы записи решения задач: по действиям; по действиям с пояснением; с вопросами; выражением. Рассмотрим различные формы записи решения на примере конкретной задачи:
а) Решение по действиям:
Ответ: 50 книг на третьей полке.
б) По действиям с пояснением:
1) 28+12=40 (к.) - на первой и второй полках вместе,
2) 90 - 40=50 (к.) - на третьей полке.
в) С вопросами:
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
Ответ: 50 книг на третьей полке, г) Выражением:
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так: 90-(28+12) = 50 (к.)
Ответ: 50 книг на третьей полке.
Не следует путать такие понятия, как: решение задачи различными способами (практический, арифметический, графический, алгебраический); различные формы записи арифметического способа решения задачи (по действиям, выражением, по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомыми, а следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
1) 90 - 28 = 62 (к.) - на второй и третьей полке,
2) 62 - 12 = 50 (к.) - на третьей полке.
Ответ: 50 книг на третьей полке.
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
1) 90 - 12 = 78 (к.) - на первой и третьей полке,
2) 78 - 28 = 50 (к.) - на третьей полке.
1-й вариант 1-й способ: 1) 60-4=240 (км), 2) 520 - 240=280 (км),
3) 280:4=70 (км/ч). 2-й способ: (520-60-4):4.
1-й способ: 1) 60 • 4=240 (км), 2) 520 - 240=280 (км), 3) 280:4=70 (км/ч).
2-й способ: 1) 520:4=130 (км/ч), 2) 130 - 60=70 (км/ч).
1-й вариант 1-й способ: 1) 15+12=27 (м), 2) 27: 3=9 (п.).
Ответ: 9 платьев скроили. 2-й способ: 15:3+12:3
Ответ: 9 платьев скроили.
2-й вариант 1-й способ: 1) 15:3=5 (п.),
Ответ: 9 платьев скроили. 2-й способ: 15:3+12:3
Ответ: 9 платьев скроили.
В числе способов решения задач можно назвать схематическое моделирование. В отличие от графического способа решения, который позволяет ответить на вопрос задачи, используя счет и присчитывание, схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство). Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить на вопрос задачи. Покажем это на конкретных примерах:
В двух вагонах ехали пассажиры, по 36 человек в каждом вагоне. На станции из первого вагона вышло несколько человек, а из второго вагона вышло столько, сколько осталось в первом. Сколько всего пассажиров осталось в двух вагонах?
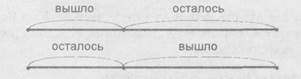 |
| Ответ: в двух вагонах осталось 36 человек. |
В данном случае схема выступает как способ и как форма записи решения задачи.
• Если цену учебника уменьшить в 3 раза, то получим цену блокнота. Блокнот в три раза дороже тетради. Краски в 9 раз дороже тетради. Хватит ли денег, которые мама дала для покупки учебника, на покупку красок?
Ответ на вопрос задачи можно дать, если с помощью отрезков смоделировать данные в задаче отношения.
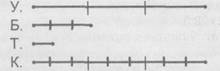
Ответ: денег на покупку красок хватит.
Используя знания о математических отношениях, маленькие школьники с удовольствием решают такие задачи.
Возможен и комбинированный способ. В этом случае для записи решения задачи могут быть использованы одновременно схема и числовые равенства.
, =, чтобы получились верные записи: 3 . 5, 8 . 4.
Условие задачи - числа 3 и 5, 8 и 4. Требование - сравнить эти числа.
Реши уравнение: х + 4 = 9.
В условии дано уравнение. Требование - решить его, т. е. подставить вместо х такое число, чтобы получилось истинное равенство.
• Выбери из данных фигур те, из которых можно сложить прямоугольник.

Здесь в условии даны треугольники. Требование - сложить прямоугольник.
Для выполнения каждого требования применяется определенный метод или способ действия, в зависимости от которого выделяют различные виды математических задач: на построение, доказательство, преобразование, комбинаторные задачи, арифметические и т. д.
При обучении младших 'школьников математике решению этих задач уделяется большое внимание. Это обусловлено следующим,
1. В сюжетах находят отражение практические ситуации, имеющие место в жизни ребенка. Это помогает ему осознать реальные количественные отношения между различными объектами (величинами) и тем самым углубить и расширить свои представления о реальной действительности.
2. Решение этих задач позволяет ребенку осознать практическую значимость тех математических понятий, которыми он овладевает в начальном курсе математики.
3. В процессе их решения у ребенка можно формировать умения, необходимые для решения любой математической задачи (выделять данные и искомое, условие и вопрос, устанавливать зависимость между ними, строить умозаключения, моделировать, проверять полученный результат).
Рассмотрим различные способы решения текстовых задач на конкретном примере:
• Задача. Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т. д., пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ решения можно назвать практическим или предметным. Его возможности ограничены, так как учащиеся могут выполнить предметные действия только с небольшими количествами. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практически, а арифметическим способом, записав равенство: 8:2 = 4
Для решения можно применить алгебраический способ, рассуждая при этом так: «Число тарелок неизвестно, обозначим их буквой х. На каждой тарелке 2 яблока, значит, число всех яблок - это '2-х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2-х=8 и решить его: х = 8:2, х = 4.
Ту же задачу можно решить графическим способом, изобразив каждое яблоко отрезком. Этот способ решения близок к практическому, но носит более абстрактный характер и требует специального разъяснения.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называют простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называют составными. Составную задачу, так же как и простую, можно решить, используя различные способы. Например:
• Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные - щуки. Сколько щук поймал рыбак?
Практический способ.
 |
| Для ответа на вопрос задачи можно не выполнять арифметические действия, т. к. количество пойманных щук соответствует тем «ругам, которые не обозначены (их 3). |
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим пойманных рыб: л - лещи, о - окуни.
Арифметический способ.
1) 3 + 4 = 7 (р.) - пойманные рыбы;
2) 10 - 7 = 3 (р.) - щуки.
Для ответа на вопрос задачи мы выполнили два действия.
Алгебраический способ.
Пусть х - пойманные щуки. Тогда количество всех рыб можно записать выражением:
3 + 4 + х~ все рыбы.
По условию задачи известно, что рыбак поймал всего 10 рыб. Значит: 3 + 4 + х= 10.
Решив это уравнение, мы ответим на вопрос задачи.
Графический способ.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
|/ Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.
/ В начальных классах используются различные формы записи решения задач: по действиям; по действиям с пояснением; с вопросами; выражением. Рассмотрим различные формы записи решения на примере конкретной задачи:
а) Решение по действиям:
Ответ: 50 книг на третьей полке.
б) По действиям с пояснением:
1) 28+12=40 (к.) - на первой и второй полках вместе,
2) 90 - 40=50 (к.) - на третьей полке.
в) С вопросами:
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
Ответ: 50 книг на третьей полке, г) Выражением:
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так: 90-(28+12) = 50 (к.)
Ответ: 50 книг на третьей полке.
Не следует путать такие понятия, как: решение задачи различными способами (практический, арифметический, графический, алгебраический); различные формы записи арифметического способа решения задачи (по действиям, выражением, по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомыми, а следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
1) 90 - 28 = 62 (к.) - на второй и третьей полке,
2) 62 - 12 = 50 (к.) - на третьей полке.
Ответ: 50 книг на третьей полке.
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
1) 90 - 12 = 78 (к.) - на первой и третьей полке,
2) 78 - 28 = 50 (к.) - на третьей полке.
1-й вариант 1-й способ: 1) 60-4=240 (км), 2) 520 - 240=280 (км),
3) 280:4=70 (км/ч). 2-й способ: (520-60-4):4.
1-й способ: 1) 60 • 4=240 (км), 2) 520 - 240=280 (км), 3) 280:4=70 (км/ч).
2-й способ: 1) 520:4=130 (км/ч), 2) 130 - 60=70 (км/ч).
1-й вариант 1-й способ: 1) 15+12=27 (м), 2) 27: 3=9 (п.).
Ответ: 9 платьев скроили. 2-й способ: 15:3+12:3
Ответ: 9 платьев скроили.
2-й вариант 1-й способ: 1) 15:3=5 (п.),
Ответ: 9 платьев скроили. 2-й способ: 15:3+12:3
Ответ: 9 платьев скроили.
В числе способов решения задач можно назвать схематическое моделирование. В отличие от графического способа решения, который позволяет ответить на вопрос задачи, используя счет и присчитывание, схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство). Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить на вопрос задачи. Покажем это на конкретных примерах:
В двух вагонах ехали пассажиры, по 36 человек в каждом вагоне. На станции из первого вагона вышло несколько человек, а из второго вагона вышло столько, сколько осталось в первом. Сколько всего пассажиров осталось в двух вагонах?
 |
| Ответ: в двух вагонах осталось 36 человек. |
В данном случае схема выступает как способ и как форма записи решения задачи.
• Если цену учебника уменьшить в 3 раза, то получим цену блокнота. Блокнот в три раза дороже тетради. Краски в 9 раз дороже тетради. Хватит ли денег, которые мама дала для покупки учебника, на покупку красок?
Ответ на вопрос задачи можно дать, если с помощью отрезков смоделировать данные в задаче отношения.

Ответ: денег на покупку красок хватит.
Используя знания о математических отношениях, маленькие школьники с удовольствием решают такие задачи.
Возможен и комбинированный способ. В этом случае для записи решения задачи могут быть использованы одновременно схема и числовые равенства.
Читайте также:

