Теорема о работе равнодействующей кратко

Обновлено: 30.06.2024

Рассмотрим материальную точку М , к которой приложена сила F . Пусть точка переместилась из положения М₀ в положение М₁ , пройдя путь s (рис. 1) .

Чтобы установить количественную меру воздействия силы F на пути s , разложим эту силу на составляющие N и R , направленные соответственно перпендикулярно направлению перемещения и вдоль него. Так как составляющая N (перпендикулярная перемещению) не может двигать точку или сопротивляться ее перемещению в направлении s , то действие силы F на пути s можно определить произведением Rs .
Эта величина называется работой и обозначается W .
Следовательно,

W = Rs = Fs cos α ,

т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки.

Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении .
Работа является скалярной величиной.

Рассматривая работу силы, можно выделить три частных случая: сила направлена вдоль перемещения (α = 0˚) , сила направлена в противоположном перемещению направлении (α = 180˚) , и сила перпендикулярна перемещению (α = 90˚) .
Исходя из величины косинуса угла α , можно сделать вывод, что в первом случае работа будет положительной, во втором – отрицательной, а в третьем случае (cos 90˚ = 0) работа силы равна нулю.
Так, например, при движении тела вниз работа силы тяжести будет положительной (вектор силы совпадает с перемещением), при подъеме тела вверх работа силы тяжести будет отрицательной, а при горизонтальном перемещении тела относительно поверхности Земли работа силы тяжести будет равна нулю.

Силы, совершающие положительную работу, называются движущимися силами , силы, а совершающие отрицательную работу – силами сопротивления .

Единицей работы принят джоуль (Дж):
1 Дж = сила×длина = ньютон×метр = 1 Нм.

Джоуль – это работа силы в один ньютон на пути в один метр.

Работа силы на криволинейном участке пути

На бесконечно малом участке ds криволинейный путь можно условно считать прямолинейным, а силу – постоянной.
Тогда элементарная работа dW силы на пути ds равна

dW = F ds cos (F , v) .

Работа на конечном перемещении равна сумме элементарных работ:

W = ∫ F cos (F , v) ds .

На рисунке 2а изображен график зависимости между пройденным расстоянием и F cos (F , v) . Площадь заштрихованной полоски, которую при бесконечно малом перемещении ds можно принять за прямоугольник, равна элементарной работе на пути ds :

dW = F cos (F , v) ds ,

а работа силы F на конечном пути s графически выражается площадью фигуры ОАВС , ограниченной осью абсцисс, двумя ординатами и кривой АВ , которая называется кривой сил .

Если работа совпадает с направлением перемещения и возрастает от нуля пропорционально пути, то работа графически выражается площадью треугольника ОАВ (рис. 2 б) , которая, как известно, может быть определена половиной произведения основания на высоту, т. е. половиной произведения силы на путь:

Теорема о работе равнодействующей

Теорема: работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том же участке пути .

Пусть к материальной точке М приложена система сил (F₁ , F₂ , F₃ . F_n) , равнодействующая которых равна F_Σ (рис. 3) .

Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,

Спроецируем это векторное равенство на касательную к траектории, по которой движется материальная точка, тогда:

Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем полученное равенство в пределах какого-то конечного перемещения s :

что соответствует равенству:

Теорема о работе силы тяжести

Теорема: работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения .

Пусть материальная точка М движется под действием силы тяжести G и за какой-то промежуток времени перемещается из положения М₁ в положение М₂ , пройдя путь s (рис. 4) .
На траектории точки М выделим бесконечно малый участок ds , который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна.
Из заштрихованного треугольника получим, что

Элементарная работа силы G на пути ds равна:

Полная работа силы тяжести G на пути s равна

W = ∫ Gds cos α = ∫ Gdy = G ∫ dy = Gh .

Итак, работа силы тяжести равна произведению силы на вертикальное перемещение точки ее приложения:

Пример решения задачи по определению работы силы тяжести

Задача: Однородный прямоугольный массив АВСD массой m = 4080 кг имеет размеры, указанные на рис. 5 .
Определить работу, которую необходимо выполнить для опрокидывания массива вокруг ребра D .

Решение.
Очевидно, что искомая работа будет равна работе сопротивления, совершаемой силой тяжести массива, при этом вертикальное перемещение центра тяжести массива при опрокидывании через ребро D является путем, который определяет величину работы силы тяжести.

Для начала определим силу тяжести массива: G = mg = 4080×9,81 = 40 000 Н = 40 кН .

Для определения вертикального перемещения h центра тяжести прямоугольного однородного массива (он находится в точке пересечения диагоналей прямоугольника), используем теорему Пифагора, исходя из которой:

КО₁ = ОD – КD = √(ОК 2 + КD 2 ) – КD = √(3 2 +4 2 ) - 4 = 1 м .

На основании теоремы о работе силы тяжести определим искомую работу, необходимую для опрокидывания массива:

W = G×КО₁ = 40 000×1 = 40 000 Дж = 40 кДж.

Работа постоянной силы, приложенной к вращающемуся телу

Представим себе диск, вращающийся вокруг неподвижной оси под действием постоянной силы F (рис. 6) , точка приложения которой перемещается вместе с диском. Разложим силу F на три взаимно-перпендикулярные составляющие: F₁ – окружная сила, F₂ – осевая сила, F₃ – радиальная сила.

При повороте диска на бесконечно малый угол dφ сила F совершит элементарную работу, которая на основании теоремы о работе равнодействующей будет равна сумме работ составляющих.

Очевидно, что работа составляющих F₂ и F₃ будет равна нулю, так как векторы этих сил перпендикулярны бесконечно малому перемещению ds точки приложения М , поэтому элементарная работа силы F равна работе ее составляющей F₁ :

При повороте диска на конечный угол φ работа силы F равна

где угол φ выражается в радианах.

Так как моменты составляющих F₂ и F₃ относительно оси z равны нулю, то на основании теоремы Вариньона момент силы F относительно оси z равен:

Момент силы, приложенной к диску, относительно оси вращения называется вращающим моментом, и, согласно стандарту ИСО, обозначается буквой Т :

Т = М_z(F) , следовательно, W = Tφ .

Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловое перемещение .

Пример решения задачи

Задача: рабочий вращает рукоятку лебедки силой F = 200 Н , перпендикулярной радиусу вращения.
Найти работу, затраченную в течение времени t = 25 секунд , если длина рукоятки r = 0,4 м , а ее угловая скорость ω = π/3 рад/с .

Решение.
Прежде всего определим угловое перемещение φ рукоятки лебедки за 25 секунд :

φ = ωt = (π/3)×25 = 26,18 рад.

Далее воспользуемся формулой для определения работы силы при вращательном движении:

W = Tφ = Frφ = 200×0,4×26,18 ≈ 2100 Дж ≈ 2,1 кДж .

Мощность

Работа, совершаемая какой-либо силой, может быть за различные промежутки времени, т. е. с разной скоростью. Чтобы охарактеризовать, насколько быстро совершается работа, в механике существует понятие мощности , которую обычно обозначают буквой P .

Мощностью называется работа, совершаемая в единицу времени.

Если работа совершается равномерно, то мощность определяют по формуле

Если направление силы и направление перемещения совпадают, что эту формулу можно записать в иной форме:

P = W/t = Fs/t или P = Fv .

Мощность силы равна произведению модуля силы на скорость точки ее приложения .

Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле:

P = W/t = Tφ/t или P = Tω .

Мощность силы, приложенной к равномерно вращающемуся телу, равна произведению вращающего момента на угловую скорость .

Единицей измерения мощности является ватт (Вт):

Ватт = работа/время = джоуль в секунду.

Понятие об энергии и КПД

Способность тела при переходе из одного состояния в другое совершать работу называется энергией . Энергия есть общая мера различных форм движения материи.

В механике для передачи и преобразования энергии применяются различные механизмы и машины, назначение которых – выполнение заданных человеком полезных функций. При этом энергия, передаваемая механизмами, называется механической энергией , которая принципиально отличается от тепловой, электрической, электромагнитной, ядерной и других известных видов энергии. Виды механической энергии тела мы рассмотрим на следующей странице, а здесь лишь определимся с основными понятиями и определениями.

При передаче или преобразовании энергии, а также при совершении работы, имеют место потери энергии, поскольку механизмы и машины, служащие для передачи или преобразования энергии преодолевают различные силы сопротивления (трения, сопротивления окружающей среды и т. п.). По этой причине часть энергии при передаче безвозвратно теряется и не может быть использована для выполнения полезной работы.

Коэффициент полезного действия

Часть энергии, потерянная при ее передаче на преодоление сил сопротивления, учитывается при помощи коэффициента полезного действия механизма (машины), передающего эту энергию.
Коэффициент полезного действия (КПД) обозначается буквой η и определяется, как отношение полезной работы (или мощности) к затраченной:

Если коэффициент полезного действия учитывает только механические потери, то его называют механическим КПД.

Очевидно, что КПД – всегда правильная дробь (иногда его выражают в процентах) и его значение не может быть больше единицы. Чем ближе значение КПД к единице (100 %) , тем экономичнее работает машина.

Если энергия или мощность передаются рядом последовательных механизмов, то суммарный КПД может быть определен, как произведение КПД всех механизмов:

где: η₁ , η₂ , η₃ , . η_n – КПД каждого механизма в отдельности.

Пусть к материальной точке М приложена система сил (F₁, F₂, F₃,…, F_n), равнодействующая которых равнаF (рис. 15.3).

Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,

Спроецируем это векторное равенство на касательную к траектории, тогда

Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем это равенство в пределах какого-то конечного перемещения s:

что дает равенство

Пример 15.1. Вычислить работу, которая производится при равномерном подъеме груза G= 200 Н по наклонной плоскости на расстояние s = 6 м, если угол, образуемый плоскостью с горизонтом, =30°, а коэффициент трения скольжения равен f = 0,01 (рис. 15.4).

Решение. Разложим силу тяжести G груза на две взаимно перпендикулярные составляющие G₁ и G₂— соответственно параллельную и перпендикулярную наклонной плоскости. Согласно второму закону трения скольжения, сила трения F_тр равна

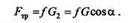
Применив теорему о работе равнодействующей, вычислим искомую работу как сумму работ сил сопротивления (работа силы G₂ и нормальной реакции Nравна нулю, так как эти силы перпендикулярны направлению перемещения s):

Подставив числовые значения, получим

Теорема о работе силы тяжести

Теорема. Работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения.

Пусть материальная точка М движется под действием одной лишь силы тяжести G и за какой-то промежуток времени перемещается из положения М₁в положение М₂, пройдя путь s (рис. 15.5).

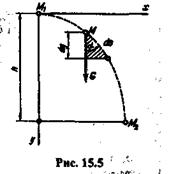
На траектории точки М выделим бесконечно малый участок ds, который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна. Из заштрихованного треугольника получим, что

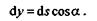
Элементарная работа силы G на пути ds

Полная работа на пути s равна

Силы, работа которых не зависит от вида траектории, называются потенциальными. К числу таких сил относятся, например, силы тяжести, силы всемирного тяготения, натяжение пружины.

Пример 15.2. Однородный массив ABCD массой т = 4080 кг имеет размеры, указанные на рис 15.6. Определить работу, которую необходимо затратить на опрокидывание массива вокруг ребра D.

Решение. Определим силу тяжести G массива:

G = mg = 4080 9,81 = 40 10 3 Н = 40 кН.

Работа, которую необходимо затратить на опрокидывание массива, равна работе силы сопротивления, т. е. силы тяжести. Для того чтобы опрокинуть массив, необходимо его центр тяжести О (находящийся в геометрическом центре, так как массив однородный) перевести в положение O₁, после чего массив продолжит опрокидываться под действием силы тяжести, которая превратится из силы сопротивления в движущую силу.

Искомую работу определим, применив теорему о работе силы тяжести:

Работа постоянной силы,

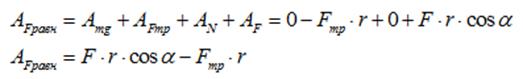
Работа - это скалярная величина, которая определяется по формуле

Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.

Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.

Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.

Теорема. Работа равнодействующей нескольких сил на некотором пути равна алгебраической сумме работ составляющих сил на том же пути.

Пусть к материальной точке , перемещающейся m положения в положение по любой криволинейной траектории, приложено несколько сил

(рис. 211). Равнодействующую данных сил обозначим через . Приняв за ось проекций ось, имеющую направление скорости точки приложения силы, будем иметь:

Умножая обе части равенства на элементарное перемещение точки приложения сил и интегрируя полученное выражение в соответствующих пределах вдоль дуги , получим:

Так как интегралы в обеих частях последнего равенства представляют собой согласно формуле (190) выражения работы соответствующих сил на конечном перемещении точки приложения этих сил, то теорема доказана.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Читайте также: