Степенная функция ее график и свойства кратко

Обновлено: 05.07.2024

В данной публикации мы рассмотрим определение и формулу степенной функции, а также покажем возможные виды ее графиков (прямая, гипербола, парабола и т.д.).

Определение степенной функции

Степенная функция – это функция вида , где:

a – показатель степени, является действительным числом, a ≠ 0;
x – основание степени, это свободная переменная.

Примеры:

К степенной часто относят функцию вида , где k – любой ненулевой коэффициент.

График степенной функции

Вид графика зависит от того, какие значения принимают показатель степени a и коэффициент k функции.

К степенным функциям в теории относятся следующие виды:

линейная функция \(y = kx + b\) ;
квадратичная парабола \(y = x^\) (в общем виде: \(y = ax^ + bx + c)\) ;
кубическая парабола \(y = x^\) ;
гипербола \(y = \frac\) , которую можно представить в виде \( y = x^;\)
функция \(y =\sqrt\) , так как \(\sqrt = x^<\frac>.\)

В качестве примера можно рассмотреть описание функции: \(y=x^>\) . В первую очередь следует проанализировать функции с показателем степени \(\frac>1\) . Например, задана некая функция:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исходя из обозначения, при x≥0, область определения рассматриваемой функции – это луч [0;+∞).

Далее следует записать таблицу значений:

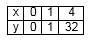
Затем можно сравнить несколько степенных функции следующим способом:

Число 2,5 находится между 2 и 3. В таком случае можно предположить, что и график рассматриваемой функции расположен между соответствующими графиками. Можно представить разные характеристики х, чтобы сравнить значения функций, которые зависят от x:

При \(0 , получается \(x^6 , но и выполняется \(\sqrt или \(x^3

При \(x>1\) , получается \(x^4 , но и выполняется \(\sqrt или \(x^2

Все графики целесообразно построить на одном рисунке. В первом случае \(0 :

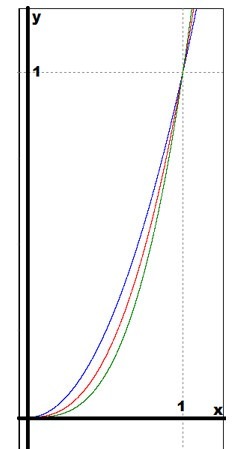
В данном случае синий цвет соответствует функции \(y=x^2\) ; красный: \( y=x^\) ; зеленый: \(y=x^3\) . На следующем этапе нужно построить графики по порядку на всей области определения функции \(y=x^\) . Цвет графиков останется прежним, как и на предыдущем рисунке:

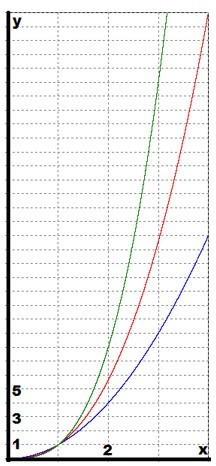
График функции \(y=x^>\) , \((m>n)\) является кривой, которая проходит через точки (0,0) и (1,1), и напоминает ветвь параболы. При увеличении показателя график функции в верхнем положении становится круче.

Линейная функция y = kx + b. Графиком данной функции является прямая линия. Для того, чтобы ее построить, требуется пара точек. При k > 0, линейная функция будет расти. При увеличении k график становится круче. Значение k представляет собой угловой коэффициент прямой и равно тангенсу угла наклона рассматриваемой прямой к положительному направлению оси X:

При использовании k

При k = 0, на графике будет изображена прямая y = b, которая параллельна оси X. В том случае, когда имеет место равенство угловых коэффициентов прямых, прямые будут параллельны друг другу.

Квадратичная функция \(y = ax2 + bx + c\) представляет собой параболу. Она обладает рядом особенностей:

Функция \(y = x^\) является кубической параболой. Можно представить ее на рисунке, а также функции \( y = x^\) и \(y = x^.\)

Можно отметить, что функции \(y = x^\) и \(y = x^\) обладают некоторыми сходствами. Графики являются симметричными по отношению к оси Y. В данном случае можно сказать, что рассматриваемые функции – четные.

Функция \(y = f(x)\) является четной, когда:

область определения функции симметрична относительно нуля;
каждое значение x из области определения соответствует справедливому равенству \(f(−x) = f(x)\) .

Графики функций \(y = x^\) и \(y = x^\) симметричны по отношению к началу координат. Данные функции являются нечетными.

Функция \(y = f(x)\) – нечетная, при условии, что:

область определения функции симметрична относительно нуля;
любой x из области определения соответствует равенству \(f(-x) = -f(x)\) .

Функция \(\small y = \frac\) в виде гиперболы также представляет собой степенную функцию. Это объясняется тем, что \(\small \frac = x^\) . Так как знаменатель не должен быть равен нулю, рассматриваемая функция не определена при \(x = 0\) . Гипербола представляет собой нечетную функцию с графиком, который симметричен по отношению к началу координат.

Построение графика функции \(\small y = \sqrt\) следует начинать с области определения. Выражение \(\small \sqrt\) определено при \(x ≥ 0\) . Поэтому областью определения функции являются все неотрицательные числа. Также \(\small y = \sqrt\) принимает только неотрицательные значения, поскольку \(\small \sqrt ≥ 0.\)

Целесообразно воспользоваться данными свойствами в процессе решения уравнений и неравенств. Уравнение вида \(\small \sqrt=g(x)\) имеет смысл только при \(f(x) ≥ 0\) и \(g(x) ≥ 0\) . Это является областью допустимых значений.

На одном графике можно построить параболу \( y = x^\) и функцию \(\small y = \sqrt\) . Следует рассмотреть правую ветвь параболы, при \(x ≥ 0\) . Заметим, что эта часть параболы и график функции \(\small y = \sqrt\) словно нарисованы по одному шаблону, по-разному расположенному в координатной плоскости. Они симметричны относительно прямой y = x.

То, что для одной из них является областью определения, для другой — представляет собой область значений. Данные функции носят название взаимно-обратных.

Виды и их свойства, область определения

Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.

D(y)=[0;+∞);
функцию нельзя отнести ни к четной, ни к нечетной;
возрастает на [0;+∞);
не имеет ограничений в верхней части, но ограничена в нижней;
отсутствует максимальное значение, минимальное значение равно нулю;
непрерывность;
E(f)=[0; +∞);
выпукла вниз.

В качестве примера можно рассмотреть случай, когда показатель степени является правильной дробью, у которой значение числителя меньше, чем знаменателя. График функции \( y=x^>\) , \((m>n)\) напоминает график функции \(y=\sqrt[n]\) :

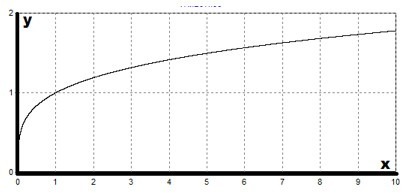
D(y)=[0;+∞);
нельзя отнести ни к четной, ни к нечетной;
возрастает на [0;+∞);
не имеет ограничений сверху, ограничена снизу;
максимальное значение отсутствует, наименьшее значение равно нулю;
непрерывность;
E(f)=[0; +∞);
выпукла вверх.

Далее следует ознакомиться с графиком функции \(y=x^>\) . Можно заметить, что он похож на гиперболу. График обладает двумя асимптотами:

График имеет следующий вид:

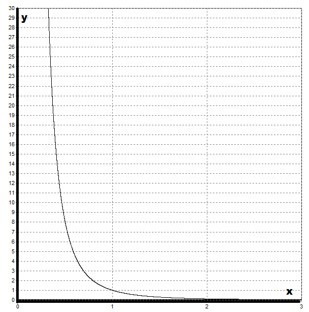
D(y)=(0;+∞);
не является ни четной, ни нечетной;
убывает на (0;+∞);
не ограничена в верхней части, обладает ограничением в нижней;
максимальное значение отсутствует, минимальное – ноль;
непрерывность;
E(f)=(0; +∞);
выпукла вниз.

В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:

Степенная функция с рациональным и иррациональным показателем

Степень действительного числа a, обладающего рациональным показателем n вычисляется, согласно уравнению:

Функция \( f(x)=x^(r\in Q)\) представляет собой степенную функцию с рациональным показателем.

Степенью числа a, которое является положительным, c иррациональным показателем \(\alpha\) называется выражение вида \(a^\) со значением, равным пределу последовательности \(a^>\) , \(a^>, a^>\) , …, где \(\alpha_, \alpha_, \alpha_\) являются последовательными десятичными приближениями иррационального числа \(\alpha\) .

Функция \(f(x)=x^(r\in J)\) представляет собой степенную функцию с иррациональным показателем.

Как строить графики степенных функций

График функции является множеством точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты – соответствующими значениями функции y.

Согласно определению, построить график какой-либо функции можно путем поиска всех пар соответствующих значений аргумента и функции. Как правило, в результате получается бесконечное множество точек, что затрудняет процесс построения графика. В связи с этим требуется исследовать функцию:

обозначить область определения и область изменения функции;
найти области ее убывания или возрастания;
определить асимптоты, интервалы знакопостоянства;
выявить несколько точек, принадлежащих графику;
соединить найденные точки плавной кривой.

Задачи со степенной функцией

Необходимо определить максимальное и минимальное значения для функции \(y=x^>\) на отрезке:

Показатель степени рассматриваемой функции обладает положительным значением. В этом случае, учитывая свойства записанной функции, можно заключить, что она возрастает на всей области определения. Таким образом, функция достигает своего максимума и минимума на концах заданных отрезков (если она определена в этих точках).

На промежутке (2,10) максимальное и минимальное значения функции отсутствуют, в связи с тем, что промежуток является открытым, и точки 0 и 4 к данному интервалу не относятся.

На луче [9;+∞) наибольшее значение отсутствует

Требуется определить максимальное и минимальное значение на отрезке [1;9] для функции:

Вычислим производную рассматриваемой функции:

Так как производная существует на всей области определения исходной функции, можно заключить, что критические точки отсутствуют.

Далее определим стационарные точки:

Заданному отрезку принадлежит только одно решение \(x_2=4\)

Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:

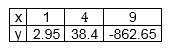
График функции \(y=x^>\) будет возрастать, а график функции \(у=24-х\) – убывать. Известно, что когда одна функция возрастает, а вторая убывает, то будет лишь одна точка, в которой эти функции пересекаются. Следовательно, уравнение обладает всего одним решением. Можно заметить, что:

Таким образом, при х=8 уравнение преобразуется в справедливое равенство: 16=16, что является ответом к задаче.

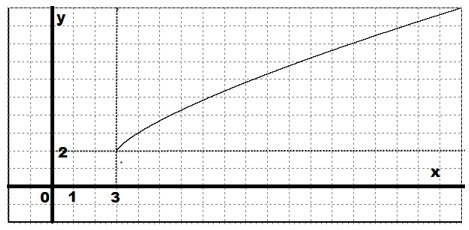
Необходимо построить график функции с объяснениями: \(y=(x-3)^\frac+2\)

График рассматриваемой функции можно получить из графика функции:

Требуется сместить этот график на 3 единицы в правую сторону и на 2 единицы вверх:

Требуется записать уравнение для касательной к прямой \(y=x^>\) в точке х=1.

В этом видеоуроке мы поговорим о степенной функции. А также познакомимся с некоторыми свойствами степенной функции в зависимости от показателя степени р.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Степенная функция, её свойства и график"

Напомним, что степенной функцией называется функция вида , где — заданное действительное число. Вы уже знакомы с частными случаями степенных функций, когда является натуральным или целым числом, например, с такими функциями, как , , , ….

Давайте вспомним, как выглядят графики этих функций.

Итак, если , то есть имеем функцию

Графиком этой функции будет прямая, проходящая через начало координат.

Если — чётное число (), то графиком функции является парабола.

Графиком функции , при нечётном (), является кубическая парабола.

Если , то . Графиком этой функции является гипербола.

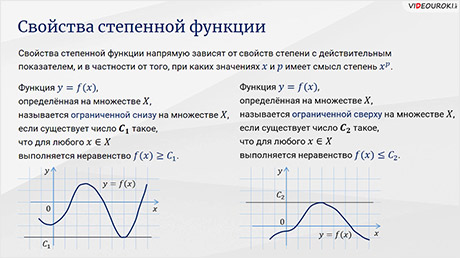
Свойства степенной функции напрямую зависят от свойств степени с действительным показателем и в частности от того, при каких значениях и имеет смысл .

Давайте рассмотрим некоторые свойствами функций, которыми обладают, в частности, отдельные степенные функции.

Итак, функция , определённая на множестве большое, называется ограниченной снизу на множестве , если существует число такое, что для любого выполняется неравенство .

Как же это понимать? Это означает, что все точки графика ограниченной снизу функции, где , расположены выше прямой игрек равно или на этой прямой.

Функция, определённая на множестве большое, называется ограниченной сверху на множестве большое, если существует число такое, что для любого , выполняется неравенство .

В этом случае все точки графика функции , где , лежат ниже прямой игрек равно или на этой прямой.

Функция является ограниченной снизу, так как . То есть парабола ограничена снизу прямой .

А функция ограничена сверху, так как , то есть парабола ограничена сверху прямой .

Функцию, ограниченную и сверху, и снизу на множестве икс большое, называют ограниченной на этом множестве.

Функция является ограниченной на множестве тогда и только тогда, когда существует положительное число такое, что для любого большое, выполняется неравенство .

Ещё вам нужно знать, что если существует такое значение из области определения множества функции ‚ что для любого из этой области справедливо неравенство , то говорят, что функция принимает наименьшее значение при .

Например, функция принимает при наименьшее значение, равное .

Если же существует такое значение из области определения множества функции , что для любого справедливо неравенство , то говорят, принимает наибольшее значение при ..

Например, функция принимает при наибольшее значение, равное 5.

А теперь давайте более подробно рассмотрим свойства степенной функции в зависимости от показателя степени .

Случай 1. Показатель — чётное натуральное число.

В этом случае степенная функция , где — натуральное число, обладает следующими свойствами:

— область определения — все действительные числа, то есть множество действительных чисел ;

— множество значений — неотрицательные числа, то есть ;

— функция чётная, так как ;

— функция является убывающей на промежутке и возрастающей на промежутке ;

— функция ограничена снизу, так как для любого ;

— функция принимает наименьшее значение при .

График функции имеет такой же вид, как, например, график функции , или и так далее. График этой функции называют параболой n-й степени.

Случай 2. Показатель — нечётное натуральное число.

В этом случае степенная функция, где — натуральное число, обладает следующими свойствами:

— область определения — множество действительных чисел;

— множество значений — множество действительных чисел;

— функция нечётная, так как ;

— функция является возрастающей на всей действительной оси;

— функция не является ограниченной ни сверху, ни снизу;

— функция не принимает ни наибольшего, ни наименьшего значения.

График функции имеет такой же вид, как, например, график функции . График этой функции называют кубической параболой.

Случай 3. Показатель , где — натуральное число.

В этом случае степенная функция, обладает следующими свойствами:

— область определения — множество действительных чисел, кроме ;

— множество значений — положительные числа ;

— функция , чётная, так как ;

— функция является возрастающей на промежутке и убывающей на промежутке ;

— функция ограничена снизу, так как ;

— функция не принимает ни наибольшего, ни наименьшего значения.

График функции имеет такой же вид, как, например, график функции .

Случай 4. Показатель , где — натуральное число.

В этом случае степенная функция , где, обладает следующими свойствами:

— область определения — множество действительных чисел, кроме ;

— множество значений — множество действительных чисел, кроме ;

— функция , нечётная, так как как ;

— функция является убывающей на промежутках и ;

— функция не является ограниченной;

— функция не принимает ни наибольшего, ни наименьшего значения.

График функции, имеет такой же вид, как, например, график функции .

Ось абсцисс является горизонтальной асимптотой, а ось ординат — вертикальной асимптотой графика функции.

Случай 5. Показатель — положительное действительное нецелое число.

В этом случае функция обладает следующими свойствами:

— область определения — множество неотрицательных чисел ;

— множество значений — множество неотрицательных чисел ;

— функция является возрастающей на промежутке ;

— функция не является ни чётной, ни нечётной;

— функция ограничена снизу, так как ;

— функция принимает наименьшее значение при .

График функции , где — положительное нецелое число, имеет такой же вид, как, например, график функции (при ) или как, например, график функции (при ).

Случай 6. Показатель — отрицательное действительное нецелое число.

В этом случае функция обладает следующими свойствами:

— область определения — множество положительных чисел ;

— множество значений — множество положительных чисел ;

— функция является убывающей на промежутке ;

— функция не является ни чётной, ни нечётной;

— функция ограничена снизу, так как .

График функции , где — отрицательное нецелое число, имеет такой же вид, как, например, график функции .

Представлены свойства и графики степенных функций при различных значениях показателя степени. Основные формулы, области определения и множества значений, четность, монотонность, возрастание и убывание, экстремумы, выпуклость, перегибы, точки пересечения с осями координат, пределы, частные значения.

Формулы со степенной функцией

На области определения степенной функции y = x p имеют место следующие формулы:
; ;
;
; ;
; ;
; .

Свойства степенных функций и их графики

Далее мы рассматриваем степенную функцию
y ( x ) = x p .

Степенная функция с показателем равным нулю, p = 0

Если показатель степенной функции y = x p равен нулю, p = 0 , то степенная функция определена для всех x ≠ 0 и является постоянной, равной единице:
y = x p = x 0 = 1, x ≠ 0 .

Степенная функция с натуральным нечетным показателем, p = n = 1, 3, 5, .

Рассмотрим степенную функцию y = x p = x n с натуральным нечетным показателем степени n = 1, 3, 5, . . Такой показатель также можно записать в виде: n = 2k + 1 , где k = 0, 1, 2, 3, . – целое не отрицательное. Ниже представлены свойства и графики таких функций.

График степенной функции y = x n с натуральным нечетным показателем при различных значениях показателя степени n = 1, 3, 5, . .

Область определения: –∞
Множество значений: –∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ выпукла вверх
при 0 выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1,
y(–1) = (–1) n ≡ (–1) 2k+1 = –1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 1 , функция является обратной к самой себе: x = y
при n ≠ 1 , обратной функцией является корень степени n :

Степенная функция с натуральным четным показателем, p = n = 2, 4, 6, .

Рассмотрим степенную функцию y = x p = x n с натуральным четным показателем степени n = 2, 4, 6, . . Такой показатель также можно записать в виде: n = 2k , где k = 1, 2, 3, . – натуральное. Свойства и графики таких функций даны ниже.

График степенной функции y = x n с натуральным четным показателем при различных значениях показателя степени n = 2, 4, 6, . .

Область определения: –∞
Множество значений: 0 ≤ y
Четность: четная, y(–x) = y(x)
Монотонность:
при x ≤ 0 монотонно убывает
при x ≥ 0 монотонно возрастает
Экстремумы: минимум, x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1 , y(–1) = (–1) n ≡ (–1) 2k = 1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 2 , квадратный корень:
при n ≠ 2 , корень степени n :

Степенная функция с целым отрицательным показателем, p = n = -1, -2, -3, .

Рассмотрим степенную функцию y = x p = x n с целым отрицательным показателем степени n = -1, -2, -3, . . Если положить n = –k , где k = 1, 2, 3, . – натуральное, то ее можно представить в виде:

График степенной функции y = x n с целым отрицательным показателем при различных значениях показателя степени n = -1, -2, -3, . .

Нечетный показатель, n = -1, -3, -5, .

Ниже представлены свойства функции y = x n с нечетным отрицательным показателем n = -1, -3, -5, . .

Область определения: x ≠ 0
Множество значений: y ≠ 0
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно убывает
Экстремумы: нет
Выпуклость:
при x : выпукла вверх
при x > 0 : выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак:
при x
при x > 0, y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = –1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –1 ,
при n ,

Четный показатель, n = -2, -4, -6, .

Ниже представлены свойства функции y = x n с четным отрицательным показателем n = -2, -4, -6, . .

Область определения: x ≠ 0
Множество значений: y > 0
Четность: четная, y(–x) = y(x)
Монотонность:
при x : монотонно возрастает
при x > 0 : монотонно убывает
Экстремумы: нет
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак: y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = 1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –2 ,
при n ,

Степенная функция с рациональным (дробным) показателем

Рассмотрим степенную функцию y = x p с рациональным (дробным) показателем степени , где n – целое, m > 1 – натуральное. Причем, n, m не имеют общих делителей.

Знаменатель дробного показателя - нечетный

Пусть знаменатель дробного показателя степени нечетный: m = 3, 5, 7, . . В этом случае, степенная функция x p определена как для положительных, так и для отрицательных значений аргумента x . Рассмотрим свойства таких степенных функций, когда показатель p находится в определенных пределах.

Показатель p отрицательный, p m = 3, 5, 7, . ) меньше нуля: .

Графики степенных функций с рациональным отрицательным показателем при различных значениях показателя степени , где m = 3, 5, 7, . - нечетное.

Нечетный числитель, n = -1, -3, -5, .

Приводим свойства степенной функции y = x p с рациональным отрицательным показателем , где n = -1, -3, -5, . - нечетное отрицательное целое, m = 3, 5, 7 . - нечетное натуральное.

Четный числитель, n = -2, -4, -6, .

Свойства степенной функции y = x p с рациональным отрицательным показателем , где n = -2, -4, -6, . - четное отрицательное целое, m = 3, 5, 7 . - нечетное натуральное.

Показатель p положительный, меньше единицы, 0

График степенной функции с рациональным показателем ( 0 ) при различных значениях показателя степени , где m = 3, 5, 7, . - нечетное.

Нечетный числитель, n = 1, 3, 5, .

Представлены свойства степенной функции y = x p с рациональным показателем , находящимся в пределах 0 , где n = 1, 3, 5, . - нечетное натуральное, m = 3, 5, 7 . - нечетное натуральное.

Область определения: –∞
Множество значений: –∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при x : выпукла вниз
при x > 0 : выпукла вверх
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Знак:
при x
при x > 0, y > 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = –1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Четный числитель, n = 2, 4, 6, .

Представлены свойства степенной функции y = x p с рациональным показателем , находящимся в пределах 0 , где n = 2, 4, 6, . – четное натуральное, m = 3, 5, 7 . – нечетное натуральное.

Область определения: –∞
Множество значений: 0 ≤ y
Четность: четная, y(–x) = y(x)
Монотонность:
при x : монотонно убывает
при x > 0 : монотонно возрастает
Экстремумы: минимум при x = 0, y = 0
Выпуклость: выпукла вверх при x ≠ 0
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Знак: при x ≠ 0, y > 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = 1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Показатель p больше единицы, p > 1

График степенной функции с рациональным показателем ( p > 1 ) при различных значениях показателя степени , где m = 3, 5, 7, . - нечетное.

Нечетный числитель, n = 5, 7, 9, .

Свойства степенной функции y = x p с рациональным показателем, большим единицы: . Где n = 5, 7, 9, . – нечетное натуральное, m = 3, 5, 7 . – нечетное натуральное.

Область определения: –∞
Множество значений: –∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ выпукла вверх
при 0 выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = –1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Четный числитель, n = 4, 6, 8, .

Свойства степенной функции y = x p с рациональным показателем, большим единицы: . Где n = 4, 6, 8, . – четное натуральное, m = 3, 5, 7 . – нечетное натуральное.

Область определения: –∞
Множество значений: 0 ≤ y
Четность: четная, y(–x) = y(x)
Монотонность:
при x монотонно убывает
при x > 0 монотонно возрастает
Экстремумы: минимум при x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = 1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Знаменатель дробного показателя - четный

Пусть знаменатель дробного показателя степени четный: m = 2, 4, 6, . . В этом случае, степенная функция x p не определена для отрицательных значений аргумента. Ее свойства совпадают со свойствами степенной функции с иррациональным показателем (см. следующий раздел).

Степенная функция с иррациональным показателем

Рассмотрим степенную функцию y = x p с иррациональным показателем степени p . Свойства таких функций отличаются от рассмотренных выше тем, что они не определены для отрицательных значений аргумента x . Для положительных значений аргумента, свойства зависят только от величины показателя степени p и не зависят от того, является ли p целым, рациональным или иррациональным.

Графики степенной функции y = x p при различных значениях показателя p .

Степенная функция с отрицательным показателем p x > 0
Множество значений: y > 0
Монотонность: монотонно убывает
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Пределы: ;
Частное значение: При x = 1, y(1) = 1 p = 1

Степенная функция с положительным показателем p > 0

Показатель меньше единицы 0 x ≥ 0
Множество значений: y ≥ 0
Монотонность: монотонно возрастает
Выпуклость: выпукла вверх
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
Частные значения: При x = 0, y(0) = 0 p = 0 .
При x = 1, y(1) = 1 p = 1

Показатель больше единицы p > 1

Область определения: x ≥ 0
Множество значений: y ≥ 0
Монотонность: монотонно возрастает
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
Частные значения: При x = 0, y(0) = 0 p = 0 .
При x = 1, y(1) = 1 p = 1

Читайте также: