Смешанная система счисления кратко
Обновлено: 05.07.2024
Системы счисления со смешанным основанием - это нестандартные позиционные системы счисления, в которых числовое основание меняется от позиции к позиции. Такое числовое представление применяется, когда величина выражается с помощью последовательности единиц, каждая из которых кратна следующей меньшей, но не в одном и том же множителе. Такие единицы распространены, например, при измерении времени; время в 32 недели, 5 дней, 7 часов, 45 минут, 15 секунд и 500 миллисекунд может быть выражено как количество минут в нотации со смешанным основанием:
СОДЕРЖАНИЕ
Самый известный пример систем со смешанным основанием - хронометраж и календари. Западная система корней времени включает десятичные века, десятилетия и годы, а также двенадцатеричные месяцы, тридесятеричные (и не десятичные и (для февраля) восьмеричные и эннеавигативные) дни, перекрытые с двумя десятичными десятичными неделями и семеричными днями. В одном варианте используются трехзначные месяцы, четвертичные недели и семеричные дни. Далее время делится на четырехзначные часы, шестидесятеричные минуты и секунды, а затем на их десятичные дроби.
Стандартная форма для дат - 2021-04-10 16:31:15, которая в этом определении будет представлять собой смешанное число с основанием системы счисления, но отличается, поскольку количество дней в месяце варьируется для каждого месяца и в високосные годы.
Для смешанной системы счисления с основанием системы счисления часто полезно использовать сводную таблицу. Система описания 604800 секунд недели, начиная с полуночи воскресенья, работает следующим образом:
В этой системе счисления смешанное число с основанием 3 7 17 24 51 60 57 60 секунд будет интерпретироваться как 17:51:57 в среду, а 0 7 0 24 02 60 24 60 будет в 00:02:24 в воскресенье. Специальные обозначения для смешанных систем счисления счисления являются обычным явлением.
Второй пример используемой в настоящее время смешанной системы счисления с основанием системы счисления - это дизайн и использование валюты , когда ограниченный набор номиналов печатается или чеканится с целью представления любой денежной суммы; количество денег тогда представлено количеством монет или банкнот каждого достоинства. При принятии решения, какие достоинства создавать (и, следовательно, какие корни смешивать), стремятся к компромиссу между минимальным количеством различных номиналов и минимальным количеством отдельных монет, необходимых для представления типичных количеств. Так, например, в Великобритании банкноты печатаются по цене 50, 20, 10 и 5 фунтов стерлингов, а монеты чеканиваются по цене 2 фунта стерлингов, 1 фунт стерлингов, 50 пенсов, 20 пенсов, 10 пенсов, 5 пенсов, 2 пенни и 1 пенни. в 1-2-5 рядов предпочтительных значений .
Обычные единицы измерения в Соединенных Штатах - это, как правило, системы счисления с разным основанием, с множителями, изменяющимися от одной единицы размера к другой так же, как и единицы времени.
Представление со смешанным основанием также актуально для версий алгоритма БПФ Кули-Тьюки со смешанным основанием , в котором индексы входных значений расширяются в представлении со смешанным основанием, индексы выходных значений расширяются в соответствующем смешанном виде Радиксное представление с обратным порядком оснований и цифр, и каждое частичное преобразование можно рассматривать как преобразование Фурье в одну цифру для всех значений остальных цифр.
Числа со смешанным основанием с одной и той же базой можно обрабатывать, используя обобщение ручных арифметических алгоритмов. Преобразование значений из одной смешанной базы в другую легко выполнить, сначала преобразуя значения разряда одной системы в другую, а затем применяя цифры из одной системы к ним.
APL и J включают операторы для преобразования в системы со смешанным основанием и обратно.
Еще одно предложение - так называемая факториальная система счисления:
Например, наибольшее число, которое может быть представлено шестью цифрами, будет 543210, что равно 719 в десятичной системе : 5 × 5! + 4 × 4! + 3 × 3! + 2 × 2! + 1 × 1! На первый взгляд это может быть неясно, но факториальная система нумерации однозначна и полна. Каждое число может быть представлено одним и только одним способом, потому что сумма соответствующих факториалов, умноженная на индекс, всегда равна следующему факториалу за вычетом единицы:
∑ я знак равно 0 п ( ( [ я + 1 ] + 1 ) - 1 ) ⋅ ( [ я ] + 1 ) ! знак равно ( [ п + 1 ] + 1 ) ! - 1 ^ (([i + 1] +1) -1) \ cdot ([i] +1)! = ([n + 1] +1)! - 1>
Между целыми числами 0, . n существует естественное отображение ! - 1 и перестановки из п элементов в лексикографическом порядке, в котором используется факторное представление целого числа, а затем интерпретации в качестве кода Лемера .
Вышеприведенное уравнение является частным случаем следующего общего правила для любого базового представления с основанием системы счисления (стандартного или смешанного), которое выражает тот факт, что любое базовое представление счисления (стандартное или смешанное) является однозначным и полным. Каждое число может быть представлено одним и только одним способом, потому что сумма соответствующих весов, умноженная на индекс, всегда равна следующему весу минус один:
что легко доказать с помощью математической индукции .
Другое предложение - это система счисления с последовательными простыми числами в качестве основания, разряды которых являются первичными числами:
старшим основанием , Q — младшим основанием , а сама система счисления называется Q-P-ичной .
В смешанной системе счисления во избежании разночтения для изображения каждой P-ичной цифры отводится одинаковое количество Q-ичных разрядов, достаточное для представления любой P-ичной цифры.
Двоично-десятичная система счисления
Примером смешанной системы счисления является двоично-десятичная система . В двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится 4 двоичных разряда, поскольку максимальная десятичная цифра 9 кодируется как 10012. Например,
Здесь последовательные четверки (тетрады) двоичных разрядов изображают цифры 9, 2 и 5 десятичной записи соответственно.
Хотя в двоично-десятичной записи используются только цифры 0 и 1, эта запись отличается от двоичного изображения данного числа. Например, двоичный код 1001 0010 0101 соответствует десятичному числу 2341, а не 925.
В случае если P=Q l (l – целое положительное число), запись любого числа в смешанной системе счисления тождественно совпадает с изображением этого числа в системе счисления с основанием Q. Примерами такой смешанной системы счисления являются двоично-восьмеричная и двоично-шестнадцатеричная.
-ичной системе. В такой системе Р называется старшим основанием, a Q — младшим основанием, а сама смешанная система называется (Q - Р)-ичной. Для того чтобы запись числа в смешанной системе счисления была однозначной, для представления любой Р-ичной цифры отводится одно и то же количество £?-ичных разрядов, достаточное для предс тавления любого базисного числа Р-ичной системы. Так, в сме шанной двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится четыре двоичных разряда. , Например, десятичное число х = 925 в двоично-десятичной системе запишется в виде 1001 0010 0101. Здесь последовательные четверки (тетрады) двоичных разрядов изображают цифры 9, 2, 5 записи числа в десятичной системе счисления. Следует обратить внимание, что хотя в двоично-десятичной записи числа и используются только цифры 0 и 1, эта запись отличается от двоичного изображения данного числа. Например, приведенный выше двоичный код в двоичной системе счисления изображает число 2341, а не число 925.
Условимся изображать принадлежность числа к (Q — /*)-ичной системе счисления с помощью нижнего индекса (Q - Р) при данном числе, например: 925ю= 100i001001012_m.
Аналогично рассмотренной выше двоично-десятичной системе можно использовать и другие смешанные системы при различных значениях Р и Q. Особого внимания заслуживает случай, когда Р = Q', где / — целое положительное число. В этом случае запись какого-либо числа в смешанной системе тождественно совпадает с изображением этого числа в системе счисления с основанием Q (что не имеет места в двоично-десятичной системе в общем случае ).
Докажем это утверждение. Рассмотрим произвольное целое число N. В Р-ичной системе счисления это число будет записано в виде
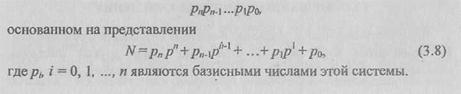

Как видно, эта запись тождественно совпадает с приведенной выше записью числа N в смешанной системе счисления, где каждая очередная группа из / цифр является просто изображением соответствующего коэффициента pf в системе счисления с осно ванием Q.
Все сказанное выше относительно целых чисел автоматически переносится и на случай произвольных чисел. Таким образом, изображение числа х в Р-ичной системе счисления в случае Р - Q является просто сокращенной записью изображения этого же числа х
в g-ичной системе.
Рассмотренное выше свойство некоторых смешанных систем широко используется на практике для сокращенной записи чисел, заданных в системе счисления с небольшим основанием. Для этого в исходной записи числа разряды объединяются вправо и влево от точки в группы некоторой длины (добавляя в случае необходимости левее старшей или правее младшей значащих цифр соответствующее количество нулей), и каждая такая группа записывается одной циф рой другой системы, основание которой равно соответствующей степени исходного основания. Например, двоичное изображение
101110.1 числа 46.5 можно записать короче с использованием цифр других систем, причем эта сокращенная запись одновременно является и изображением данного числа в соответствующей системе счисления:
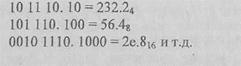 |
3.3,5. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫСЧИСЛЕНИЯ В ДРУГУЮ
При решении задач с помощью ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получить и окончательные результаты. Так как в современных ЭВМ данные кодируются в основном в двоичных кодах, то, в частности, возникает необходимость перевода чисел из десятичной в двоичную систему счисления и наоборот.
При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только такими системами счис ления, у которых базисными числами являются последовательные целые числа от 0 до Р~\ включительно, где Р — основание системы счисления.

Задача перевода заключается в следующем. Пусть известна запись числа х в системе счисления с каким-либо основанием Р:
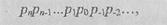
где pi — цифры r-ичной системы (0
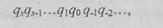
Для получения Р-ичного изображения выражения (3.11) необхо димо все цифры qt и число Q заменить Р-ичными изображениями и выполнить арифметические операции в Р-ичной системе счисления.
Пример 1.Перевести число х ~ 371В в десятичную систему счисления, пользуясь
правилами десятичной арифметики.
Для перевода запишем число х в виде х = 3*8 2 н- 7*8' + 1 и выполним все необходимые действия в десятичной системе:
Пример 2.Перевести число *=af4!6 в десятичную систему счисления, пользуясь
правилами десятичной арифметики.
Для перевода запишем число х в видел = 10х1б' + 15x16° + 4 х ! б" 1 и выполним все необходимые действия в десятичной системе:
х =10x16+ 15 + 4/16=160+15+0.25=175.25.
Заметим, что при переводе следует придерживаться правила сохранения точности изображения числа в разных системах, причем под точностью понимается значение единицы самого младшего (правого) разряда, используемого в записи числа в той или иной системе счисления.
Перевод Р —> Q. Так как для перевода любого числа достаточно уметь переводить его целую и дробную части, рассмотрим отдельно эти два случая.
1. Перевод целых чисел. Пусть известна запись целого числа ./V в системе счисления с основанием Р и требуется перевести это число в систему счисления с основанием Q. Так как N— целое, то его запись в (9-ичной системе счисления имеет вид
где q, - искомые цифры £?-ичной системы (0 4 + q. &- 1 + . + q>Q ] +q0 (3.12)
на число Q, причем в левой части произведем деление, пользуясь правилами Р-ичной арифметики (так как запись числа ./V в Р-ичной системе счисления известна), а правую часть перепишем в виде
WQ = qff 1 + q^O* +. + qi+qo/Q.
3-514 65
Приравнивая между собой полученные целые и дробные части (учитывая, что q, l + q^ff~ 2 + -+q>,
Таким образом, младший коэффициент qQ в разложении (3.12) определяется соотношением
причем указанные здесь действия на самом деле не выполняются, так как qQ является просто остатком от деления N на Q. Положим
N> = [N/Q] = qxff' 1 + g,,_>ff- 2 + . + -ичной системе счисления можно представить в виде полинома
x~q-lff l +q-2ff 2 +. + q*ff m +.~, (3.14)
где q.i (i = 1, 2, . ) — искомые коэффициенты £-ичного разложения числа х. Для определения q.\ умножим обе части равенства (3.14) на число Q, причем в левой части произведем умножение, пользуясь правилами Р-ичной арифметики (так как запись числа JE в Р-ичной системе счисления известна), а правую часть перепишем в виде
xQ = q.i +q-2Q rl +q-*Q- m + *+. '
Приравняем между собой полученные в правой части этого выражения целые и дробные части (учитывая, что 0 m *+-
Таким образом, младший коэффициент q. в разложении (3.14) определяется соотношением
q-\ = [xiQ\. Положим
Тогда х\ будет правильной дробью и к этому числу можно применить ту же самую процедуру для определения следующего коэффициента q.i и т.д.
Таким образом, при условии, что х0 = х, перевод дроби с исполь зованием Р-ичной арифметики осуществляется по следующим рекур рентным формулам:
Этот процесс продолжается до тех пор, пока не будет получено xi+i = 0 или не будет достигнута требуемая точность изображения числа.
Замечание. При переводе приближенных дробей из одной системы счисления в другую необходимо 'придерживаться следую щего правила.
Если единица младшего разряда числа л;, заданного в Р-ичной системе счисления, есть Р~, то в его g-ичной записи следует сохранить / разрядов после запятой, где / удовлетворяет условию
gi >p- k !2>Q- ( l + l \
округляя последнюю оставляемую цифру обычным способом.
Пример5. Перевести число х = 0.2 в двоичную систему счисления с использованием средств десятичной арифметики. Применение формул (3.15) при водит к такой последовательности действий:
0.2x2 = 0.4 = 0 + 0.4 =>?_, =0
Условимся изображать принадлежность числа к (Q — /*)-ичной системе счисления с помощью нижнего индекса (Q - Р) при данном числе, например: 925ю= 100i001001012_m.
Аналогично рассмотренной выше двоично-десятичной системе можно использовать и другие смешанные системы при различных значениях Р и Q. Особого внимания заслуживает случай, когда Р = Q', где / — целое положительное число. В этом случае запись какого-либо числа в смешанной системе тождественно совпадает с изображением этого числа в системе счисления с основанием Q (что не имеет места в двоично-десятичной системе в общем случае ).
Докажем это утверждение. Рассмотрим произвольное целое число N. В Р-ичной системе счисления это число будет записано в виде
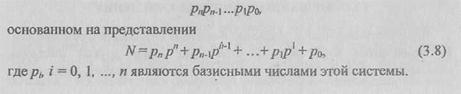

Как видно, эта запись тождественно совпадает с приведенной выше записью числа N в смешанной системе счисления, где каждая очередная группа из / цифр является просто изображением соответствующего коэффициента pf в системе счисления с осно ванием Q.
Все сказанное выше относительно целых чисел автоматически переносится и на случай произвольных чисел. Таким образом, изображение числа х в Р-ичной системе счисления в случае Р - Q является просто сокращенной записью изображения этого же числа х
в g-ичной системе.
Рассмотренное выше свойство некоторых смешанных систем широко используется на практике для сокращенной записи чисел, заданных в системе счисления с небольшим основанием. Для этого в исходной записи числа разряды объединяются вправо и влево от точки в группы некоторой длины (добавляя в случае необходимости левее старшей или правее младшей значащих цифр соответствующее количество нулей), и каждая такая группа записывается одной циф рой другой системы, основание которой равно соответствующей степени исходного основания. Например, двоичное изображение
101110.1 числа 46.5 можно записать короче с использованием цифр других систем, причем эта сокращенная запись одновременно является и изображением данного числа в соответствующей системе счисления:
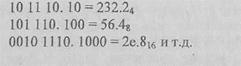 |
3.3,5. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫСЧИСЛЕНИЯ В ДРУГУЮ
При решении задач с помощью ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получить и окончательные результаты. Так как в современных ЭВМ данные кодируются в основном в двоичных кодах, то, в частности, возникает необходимость перевода чисел из десятичной в двоичную систему счисления и наоборот.
При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только такими системами счис ления, у которых базисными числами являются последовательные целые числа от 0 до Р~\ включительно, где Р — основание системы счисления.
Задача перевода заключается в следующем. Пусть известна запись числа х в системе счисления с каким-либо основанием Р:
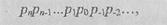
где pi — цифры r-ичной системы (0
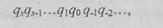
Для получения Р-ичного изображения выражения (3.11) необхо димо все цифры qt и число Q заменить Р-ичными изображениями и выполнить арифметические операции в Р-ичной системе счисления.
Пример 1.Перевести число х ~ 371В в десятичную систему счисления, пользуясь
правилами десятичной арифметики.
Для перевода запишем число х в виде х = 3*8 2 н- 7*8' + 1 и выполним все необходимые действия в десятичной системе:
Пример 2.Перевести число *=af4!6 в десятичную систему счисления, пользуясь
правилами десятичной арифметики.
Для перевода запишем число х в видел = 10х1б' + 15x16° + 4 х ! б" 1 и выполним все необходимые действия в десятичной системе:
х =10x16+ 15 + 4/16=160+15+0.25=175.25.
Заметим, что при переводе следует придерживаться правила сохранения точности изображения числа в разных системах, причем под точностью понимается значение единицы самого младшего (правого) разряда, используемого в записи числа в той или иной системе счисления.
Перевод Р —> Q. Так как для перевода любого числа достаточно уметь переводить его целую и дробную части, рассмотрим отдельно эти два случая.
1. Перевод целых чисел. Пусть известна запись целого числа ./V в системе счисления с основанием Р и требуется перевести это число в систему счисления с основанием Q. Так как N— целое, то его запись в (9-ичной системе счисления имеет вид
где q, - искомые цифры £?-ичной системы (0 4 + q. &- 1 + . + q>Q ] +q0 (3.12)
на число Q, причем в левой части произведем деление, пользуясь правилами Р-ичной арифметики (так как запись числа ./V в Р-ичной системе счисления известна), а правую часть перепишем в виде
WQ = qff 1 + q^O* +. + qi+qo/Q.
3-514 65
Приравнивая между собой полученные целые и дробные части (учитывая, что q, l + q^ff~ 2 + -+q>,
Таким образом, младший коэффициент qQ в разложении (3.12) определяется соотношением
причем указанные здесь действия на самом деле не выполняются, так как qQ является просто остатком от деления N на Q. Положим
N> = [N/Q] = qxff' 1 + g,,_>ff- 2 + . + -ичной системе счисления можно представить в виде полинома
x~q-lff l +q-2ff 2 +. + q*ff m +.~, (3.14)
где q.i (i = 1, 2, . ) — искомые коэффициенты £-ичного разложения числа х. Для определения q.\ умножим обе части равенства (3.14) на число Q, причем в левой части произведем умножение, пользуясь правилами Р-ичной арифметики (так как запись числа JE в Р-ичной системе счисления известна), а правую часть перепишем в виде
xQ = q.i +q-2Q rl +q-*Q- m + *+. '
Приравняем между собой полученные в правой части этого выражения целые и дробные части (учитывая, что 0 m *+-
Таким образом, младший коэффициент q. в разложении (3.14) определяется соотношением
q-\ = [xiQ\. Положим
Тогда х\ будет правильной дробью и к этому числу можно применить ту же самую процедуру для определения следующего коэффициента q.i и т.д.
Таким образом, при условии, что х0 = х, перевод дроби с исполь зованием Р-ичной арифметики осуществляется по следующим рекур рентным формулам:
Этот процесс продолжается до тех пор, пока не будет получено xi+i = 0 или не будет достигнута требуемая точность изображения числа.
Замечание. При переводе приближенных дробей из одной системы счисления в другую необходимо 'придерживаться следую щего правила.
Если единица младшего разряда числа л;, заданного в Р-ичной системе счисления, есть Р~, то в его g-ичной записи следует сохранить / разрядов после запятой, где / удовлетворяет условию
gi >p- k !2>Q- ( l + l \
округляя последнюю оставляемую цифру обычным способом.
Пример5. Перевести число х = 0.2 в двоичную систему счисления с использованием средств десятичной арифметики. Применение формул (3.15) при водит к такой последовательности действий:

Повторяем перевод чисел из десятичной системы счисления в любую другую систему счисления и обратно. Далее рассматриваем смешанные системы счисления, двоично-восьмеричную и двоично-шестнадцатеричную. Показываем, что такое таблицы соответствия и как с ними можно работать. Вводим понятие триады и тетрады и переводим восьмеричное число, затем шестнадцатеричное число в двоичную систему счисления и обратно. В конце поясняем, где, когда и почему удобно хранить числа в шестнадцатеричной и восьмеричной системе счисления, а не в двоичной.
Если после просмотра видео у вас возникли вопросы, то можете задать их в комментриях.
Читайте также:

