Силы инерции при ускоренном поступательном движении системы отсчета кратко

Обновлено: 02.07.2024

Ни для кого не секрет, что законы Ньютона могут быть выполнены лишь в инерциальных системах отсчета.

Системы отсчета, совершающие ускоренное движение относительно инерциальной системы, носят название неинерциальных.

В таких системах законы Ньютона применяться не могут. Несмотря на это, законы динамики можно использовать и в условиях подобных систем в случае, если, кроме обусловленных взаимным воздействием тел друг на друга сил, будет введено понятие силы инерции.

С учетом сил инерции второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета эквивалентно совокупности всех оказывающих воздействие на данное тело сил F , в список которых включены и инерционные.

Наряду с этим, силы инерции F i n должны быть такими, чтобы в сумме с силами F они придавали движению приведенного объекта ускорение a ′ , которым оно обладает в неинерциальных системах отсчета, таким образом:

По причине того, что F = m a , где a является ускорением тела в инерциальной системе отсчета.

Силы инерции вызваны ускоренным движением системы отсчета относительно исследуемой системы, из-за чего, в общем случае, стоит учитывать следующие варианты возникновения данных сил:

Силы инерции в условиях ускоренного поступательного движения системы отсчета.
Силы инерции, оказывающие воздействие на тело, покоящееся во вращающейся системе отсчета.
Силы инерции, действующие на движущееся во вращающейся системе отсчета тело.

Рассмотрим приведенные случаи.

Силы инерции в условиях ускоренного поступательного движения системы отсчета

К расположенному на тележке штативу с помощью нити подвешен шарик с некоторой массой m (рис. 1 ). Во время того, как тележка покоится или движется прямолинейно и равномерно, удерживающая шарик нить, находится в вертикальном положении, а сила тяжести P компенсируется силой натяжения нити T .

В условиях, в которых тележка обладает ускорением a 0 , нить будет отклоняться от вертикали в обратную по отношению к направлению движения сторону до некоторого угла a до тех пор, пока результирующая сила F = P + T не приведет ускорение шарика к ускорению, равному a 0 . Таким образом, результирующая сила F сонаправлена с ускорением тележки a 0 и для установившегося движения шарика (так как теперь он движется вместе с тележкой с ускорением a 0 ) эквивалентна F = m g · t g α = m a 0 , соответственно t g a = a 0 g . Выходит, что угол отклонения нити от вертикали тем больше, чем выше значение ускорения тележки. В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик находится в состоянии покоя. Такое становится возможным, если сила F компенсируется равной и противоположно направленной ей силой F i n , представляющей собой силу инерции, так как действия на шарик каких-либо других сил эффекта не возымеют.

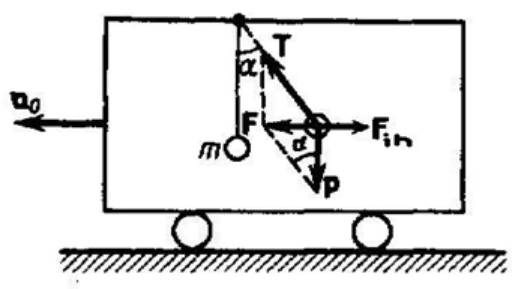
Следовательно: F i n = - m a 0 .

Силы инерции, оказывающие воздействие на тело, покоящееся во вращающейся системе отсчета

Пускай диск равномерно вращается с угловой скоростью ω ( ω = c o n s t ) вокруг ортогональной (то есть перпендикулярной) ему оси, проходящей через его центр. На диске расположены маятники, на различных расстояниях от оси вращения и на нитях прикреплены шарики массой m . Во время вращения диска, шарики отклоняются от вертикали на некоторый угол (рис. 2 ).

В инерциальной системе отсчета, связанной, к примеру, с помещением, в котором расположен диск, происходит равномерное вращательное движение шарика по окружности с радиусом R . Следовательно, на него оказывает воздействие сила, эквивалентная F = m ω 2 R и направленная ортогонально оси вращения диска. Она представляет собой равнодействующую сил тяжести и натяжения нити T : F = P + T . В момент, когда движение шарика установится, F = m g · t g a = m ω 2 R , соответственно: t g α = ω 2 R g . Таким образом, углы отклонения нитей маятников будут тем больше, чем больше величины угловой скорости вращения и расстояния R от центра шарика до оси вращения диска. Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно лишь в том случае, если сила F будет скомпенсирована равной и противоположно направленной ей силой F c , представляющей собой силу инерции, так как действия на шарик каких-либо других сил эффекта не возымеют. Сила F c , носящая название центробежной силы инерции, направлена по горизонтали от оси вращения диска и равняется:

F c = - m a 0 ω 2 R .

Исходя из формулы, расположенной выше, можно заключить, что центробежная сила инерции, воздействующая на тела во вращающихся системах отсчета и направленная в сторону радиуса от оси вращения, обладает зависимостью от угловой скорости вращения ω системы отсчета и радиуса R , однако не имеет зависимости от скорости тела относительно вращающихся систем отсчета. Таким образом, центробежная сила инерции во вращающихся системах отсчета оказывает влияние на любые удаленные от оси вращения на конечное расстояние объекты. При данном условии не имеет значения, покоятся ли они в подобной системе отсчета, как нами предполагалось до этих пор, или совершают движение относительно нее с некоторой скоростью.

Силы инерции, действующие на движущееся во вращающейся системе отсчета тело

Пускай шарик массой m совершает движение в условиях постоянной скорости υ ' вдоль радиуса равномерно вращающегося диска

( υ ' = c o n s t , ω = c o n s t , υ ' ортогонально ω ). В случае, если диск не начинает вращательное движение, шарик перемещается по радиальной прямой и попадает в точку А . Если же диск приводится во вращение в указанном стрелкой направлении, то шарик катится по кривой O В (рис. 3 а ), при этом относительно диска его скорость υ ' меняет свое направление. Такое возможно только в том случае, если на шарик оказывает влияние сила, перпендикулярная скорости υ ' .

Чтобы спровоцировать качение шарика по вращательно двигающемуся диску вдоль радиуса, будем применять жестко укрепленный вдоль него стержень, на котором шарик движется без трения прямолинейно и равномерно со скоростью υ ' (рис. 3 б ).

В случае отклонения шарика стержень воздействует на него некоторой силой F . Шарик совершает прямолинейное равномерное движение во вращающейся системе отсчета, то есть относительно диска. Данный факт основывается на том, что сила F компенсируется приложенной к шарику силой инерции F k , ортогональной скорости υ ' . Такая сила является кориолисовой силой инерции. Можно сказать, что вектор силы Кориолиса F k направлен под прямым углом к векторам скорости υ ' объекта и угловой скорости вращения системы отсчета в соответствии с правилом правого винта.

Давайте рассмотрим пример движения тела в одном из видов неинерциальных систем отсчета. Объект находится в покое на вершине наклонной плоскости.

По прошествии какого времени тело соскользнет с поверхности, если она в момент времени е = 0 начнет движение влево в горизонтальном направлении с ускорением с 1 м / с 2 ?

Длина плоскости 1 м , угол наклона плоскости по отношению к горизонту 30 ° , коэффициент трения между телом и плоскостью 0 , 6 .

Необходимо высчитать время движения тела по наклонной плоскости.

Решение

Систему отсчета будет удобно связать с наклонной плоскостью. Однако плоскость по отношению к Земле находится в состоянии ускоренного движения. Для данного движения Земля представляет собой инерциальную систему отсчета. Выходит, что связанная с наклонной плоскостью система отсчета считается, напротив, неинерциальной, и в уравнение движения тела нужно добавить поступательную силу инерции. На двигающееся тело в связанной с наклонной плоскостью системе отсчета влияют четыре силы: сила тяжести m g , сила нормальной реакции N , сила трения F т р и поступательная сила инерции F ¯ i n = - m a ¯ .

Уравнение движения тела выглядит следующим образом:

m a 1 ¯ = m g ¯ + N ¯ + F ¯ т р + F ¯ i n , где a 1 ¯ - ускорение тела.

Спроецируем это уравнение на ось X , направленную вдоль наклонной плоскости, и ортогональную к ней ось Y .

m a 1 = m g · sin α - F т р + m a · cos α , 0 = - m g · cos α + N + m a · sin α .

Если учитывать, что F т р = μ N , из этой системы уравнений получим:

a 1 = g ( sin α - μ cos α ) + a ( cos α + μ sin α ) .

По причине того, что ускорение a 1 не обладает зависимостью от времени, время движения тела по наклонной плоскости будет равняться:

t = 2 l a 1 = 2 l g ( sin α - μ cos α ) + a ( cos α + μ sin α ) ≈ 0 , 8 с

Рассмотрим шарик, подвешенный на нити, точка подвеса которого 0' движется с ускорением a относительно некоторой инерциальной системы отсчета К. Нить подвеса отклоняется от вертикали на некоторый угол . Угол этот таков, чтобы равнодействующая F силы натяжения нити T и силы тяжести mg привела к движению шарика с ускорением a:

Так выглядит описание явления с точки зрения наблюдателя в инерциальной системе отсчета К (рис. 8.1).

Рис. 8.1. Движение шарика на нити, точка подвеса которого движется с ускорением: 1 — с точки зрения наблюдателя в инерциальной системе отсчета; 2 — с точки зрения наблюдателя в движущейся неинерциальной системе отсчета

Свяжем теперь систему отсчета К' с точкой подвеса 0'. Эта система будет неинерциальной, так как она движется с ускорением a относительно инерциальной системы К. Мы пользуемся нерелятивистской механикой, так что угол отклонения нити, равно как и силы T, mg для обоих наблюдателей одинаковы. Но для наблюдателя К' шарик находится в покое (см. рис. 1–2) С другой стороны, наблюдатель К' видит, что результирующая сил T и mg не равна нулю. Поэтому наблюдатель К' приходит к выводу, что в его системе отсчета действует какая-то сила — сила инерции , которой не было в инерциальной системе отсчета К. Выражение для силы инерции получаем из условия равновесия шарика в системе К', то есть из равенства нулю трех сил:

и из уравнения второго закона Ньютона для тела следует выражение для силы инерции при поступательном движении неинерциальной системы отсчета с ускорением a:

Этот же результат верен в общем случае для произвольного движения материальной точки в движущейся поступательно неинерциальной системе отсчета К'. Пусть скорость ее движения относительно инерциальной системы отсчета К описывается функцией , а оси обеих систем остаются параллельными. Пусть скорость движения материальной точки в системе К меняется по закону . Значит, в инерциальной системе К согласно второму закону Ньютона на точку действует сила

Скорость этой же точки для наблюдателя в системе К' равна

Значит в неинерциальной системе отсчета К' на точку действует сила

Таким образом, и в этом случае сила инерции определяется формулой

где — ускорение поступательного движения неинерциальной системы относительно инерциальной.

Видео 8.3. Маятник на тележке ускоренно скатывающейся с наклонной плоскости

Эйнштейн сформулировал принцип эквивалентности неинерциальных систем и гравитационных полей и построил на этой основе общую теорию относительности (ОТО) или теорию гравитации.

Рис. 8.2. Лифт Эйнштейна

Возникновение силы инерции при поступательном ускоренном движении системы отсчета демонстрируется в опыте, показанном на рис. 8.2.

$\overline\ne <\overline> Законы Ньютона работают в инерциальных системах отсчета. По отношению ко всем инерциальным системам ускорение тела, с которым оно перемещается, является одинаковым ( ). Любая неинерциальная система совершает движение по отношению к инерциальной системе с некоторым ускорением. Ускорение, с которым тело движется в неинерциальной системе отсчета, обозначим . При этом$
Пусть разность ускорения тела в инерциальной системе и не инерциальной равны:

$\[\Delta \overline=\overline-<\overline> $

Если неинерциальная система отсчёта перемещается поступательно, то для всех точек пространства и величина является ускорением неинерциальной системы отсчета по отношению инерциальной.

$\overline<r> При вращении неинерциальной системы отсчета в разных пространственных точках различно. Если через$
обозначить радиус-вектор, который определяет положение точки относительно неинерциальной системы отсчета, то:

$\[\Delta \overline=\Delta \overline\left(<\overline<r> >$

В неинерциальных системах отсчета не работают законы сохранения импульса и энергии, так как неинерциальные системы всегда незамкнуты.

Силы в неинерционных системах отсчета

В соответствии со вторым законом Ньютона для инерционной системы отсчета мы имеем:

$\overline=\frac<\overline<F> > \qquad (3)$

$\overline<F> где$
– равнодействующая сил, действующих на тело массы m. Используя выражения (1) и (3) получим:

$\[<\overline> $

$\overline<F> Из формулы (4) следует, что при =0$
тело будет иметь ускорение в неинерциальной системе отсчета. Этот факт можно представить, как действие на тело силы равной:

$<\overline<F> >_=-m\Delta \overline \qquad (5)$

Определение силы инерции

Силой инерции (или инерциальной силой) называют векторную величину, которая по величине равна произведению массы тела на разность его ускорений в инерциальной и неинерциальной системах отсчета. Разность ускорений берут с обратным знаком.

Характерным свойством сил инерции является их прямая пропорциональность массе тела. Поэтому силы инерции считают аналогичными силам тяготения.

Силы инерции порождаются не при взаимодействии тел, а обусловлены ускоренным движением системы отсчета. Силы инерции обусловлены свойствами системы отсчета, в которой происходит рассмотрение механического явления. Рассмотрение сил инерции не является строго необходимым, так как любое движение можно исследовать в инерциальной системе отсчета. Однако решение некоторых задач в неинерциальных системах отсчета существенно проще.

Второй закон Ньютона в неинерциальной системе отсчета

$<\overline<F> Мы видим, что для описания движения тела в неинерциальной системе отсчета можно использовать уравнения Ньютона, если к силам, которые вызваны взаимодействием тел добавить силы, которые получили название сил инерции (>_$
). Уравнение второго закона Ньютона для неинерциальной системы отсчета имеет вид:

$\[m<\overline> $

Виды инерционных сил

Силы инерции вызваны движением системы отсчета с ускорением, следовательно, нужно учитывать следующие случаи проявления этих сил:

система отсчета движется поступательно с ускорением;
тело покоится во вращающейся системе отсчета;
тело движется во вращающейся системе отсчета.

Силы инерции при поступательном движении можно наблюдать, например, когда машина увеличивает свою скорость, при этом водитель под воздействием силы инерции прижимается к спинке кресла. Если автомобиль тормозит, то сила инерции будет иметь противоположное направление и автомобилист отделяется от спинки.

Если система отсчета вращается, а тело находится в покое, то на тело действует сила, которую называют центробежной силой инерции ( ). При вращении со скоростью эта центробежная сила равна:

$F_C=-m<\omega> ^2R \qquad (7)$

где R – расстояние от тела до цента вращения.

Действию такой силы подвержены, например пилоты при выполнении фигур высшего пилотажа.

Если тело движется в неинерциальной системе отсчета равномерно и прямолинейно со скоростью " width="14" height="15" />
, а система отсчета вращается со скоростью , то на тело действует сила инерции, которую называют силой Кориолиса (>_K" width="28" height="19" />
):

$\[<\overline<F> >_K=2m\left[\overline$

Вектор силы Кориолиса направлен перпендикулярно скоростям в соответствии с правилом правого винта.

Сила Кориолиса действует не все тела, которые движутся, например, по отношению к системе отсчета, связной с Землей.

Примеры решения задач

Задание

Приведите пример явлений, которые связаны с действием силы Кориолиса.

Решение

Сила Кориолиса действует на все тела, которые перемещаются во вращающихся системах отсчета. Такими системами отсчета, строго говоря, являются все системы отсчета, связанные с Землей, так как она вращается. Например, если тело перемещается в северном полушарии в сторону севера, то на него будет действовать сила Кориолиса, которая направлена вправо в отношении движения, поэтому тело отклонится в сторону востока. Если тело станет перемещаться на юг, то сила Кориолиса будет направлена вправо, если смотреть в направлении движения, тогда тело отклоняется к западу. В этой связи в северном полушарии наблюдают сильное подмывание правых берегов рек.

Сила Кориолиса объясняет поведение маятника Фуко, который в свое время стал доказательством вращения Земли. Действие силы Кориолиса на маятник ведет к тому, что происходит вращение плоскости его колебаний около вертикали.

Задание	Какова сила инерции, действующая на материальную точку, массой m подвешенную на нити к потолку вагона, движущегося с ускорением .
Решение	Сделаем рисунок.

$\overline<F> На тело, подвешенное на нити, действуют сила тяжести, сила натяжения нити и при ускоренном движении вагона сила инерции. Если вагон перемещается с ускорением , то нить с телом будет отклоняться от вертикали до тех пор, пока сила$
, равная:

$\overline<F> =m\overline+\overline \qquad (2.1)$

не сделает ускорение рассматриваемой материальной точки равным Сила " width="15" height="16" />
будет направлена по направлению ускорения _0" width="17" height="14" />
. По модулю эта сила равна:

$F=mg \text<tg> \alpha =ma_0 \qquad (2.2)$

По отношению к системе отсчета, связанной с вагоном тело находится в покое. Это возможно только если сила " width="15" height="16" />
будет уравновешена противоположно направленной ей силой инерции >_i" width="20" height="19" />
, тогда имеем:

$<\overline<F> >_i=-m<\overline>_0$

В инерциальной системе отсчета основным уравнением движения тела является уравнение, выражающее второй закон Ньютона:

Законы Ньютона выполняются только в инерциальных системах отсчета. Относительно всех инерциальных систем данное тело движется с одинаковым ускорением .

В системах отсчета, движущихся с ускорением относительно инерциальной системы, первый закон Ньютона не выполняется. Такие системы отсчета называются неинерциальными.

При рассмотрении движения в неинерциальных системах главная задача заключатся в нахождении уравнения движения в этих системах отсчета.

Для того, чтобы в этих системах можно было применить законы динамики, кроме сил, обусловленных воздействием тел друг на друга, вводятся в рассмотрение силы особого рода – силы инерции.

Любая неинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, поэтому ускорение тела в неинерциальной системе отсчета будет отлично от .

Обозначим разность ускорения тела в инерциальной и неинерциальной системах символом :

В частном случае, когда неинерциальная система отсчета движется относительно инерциальной поступательно, ускорение тела одинаково для всех точек пространства ( =const) и представляет собой ускорение неинерциальной системы отсчета.

При решении большинства задач систему отсчета, связанную с Землей, приближенно можно считать инерциальной.

В общем случае нужно учитывать следующее проявление сил инерции:

1) силы инерции при ускоренном поступательном движении системы отсчета;

2) силы инерции, действующие на тело, покоящееся во вращательной системе отсчета;

3) силы инерции, действующие на тело, движущееся во вращательной системе отсчета;

Силы инерции при поступательном движении.

Ускорение точки в неинерциальной системе отсчета можно в соответствии с (2) представить в виде:

Подставим выражение (3) в уравнение (1) и получим:

Это и есть уравнение движения материальной точки относительно неинерциальной системы отсчета. Если в неинерциальной системе отсчета определять силу как вектор, равный произведению массы материальной точки на ее ускорение в этой системе отсчета, то правая часть уравнения (4) и является силой, действующей на материальную точку, движущуюся ускоренно в неинерциальной системе отсчета. Эта сила слагается из двух существенно различных составляющих. Первая оставляющая является результатом взаимодействия тел и проявляется в инерциальной системе отсчета.

Совсем иной характер имеет составляющая – . Она возникает не из-за взаимодействия тел, а из-за ускоренного движения системы отсчета. Она называется поступательной силой инерции. При переходе к другой ускоренно движущейся системе отсчета меняются и силы инерции. Эти силы инерции отличаются от настоящих сил, возникающих при взаимодействии тел. Второе отличие состоит в том, что силы инерции не подчиняются закону действия и противодействия (третьему закону Ньютона).

При описании движения тел относительно ускоренно движущейся поступательно системы отсчета наряду с силами, обусловленными взаимодействием тел друг с другом, необходимо учитывать так называемые силы инерции . Эти силы следует полагать равными произведению массы тела на взятое с обратным знаком ускорение движущейся неинерциальной системы отсчета относительно инерциальной системы:

Соответственно, уравнение движения в неинерциальной системе отсчета будет иметь вид

Существует много явлений, в которых проявляется действие сил инерции (пассажиры в вагоне поезда, набирающего скорость, испытывают действие силы, направленной против движения поезда, силы инерции вызывают перегрузки, действующие на летчика при больших ускорениях самолета). Если в ускоренно движущемся вагоне висит шарик массы m, то сила инерции отклоняет его в сторону, противоположную ускорению (рис.1).

Рис.1

Нить отклоняется на такой угол, чтобы результирующая двух сил ( ) сообщала шарику ускорение , с которым движется вагон. Относительно системы отсчета, связанной с вагоном, шарик покоится. Это можно объяснить, если ввести силу инерции , уравновешивающую результирующую двух сил и .

Введение сил инерции дает возможность описывать движение тел в любых системах отсчета с помощью одних и тех же уравнений движения.

Особенности сил инерции:

1) они не отражают взаимодействие тел, а обусловлены характером неинерциальных систем отсчета, поэтому для сил инерции неприменим третий закон Ньютона;

2) силы инерции пропорциональны массе тела. Благодаря этому свойству силы инерции оказываются аналогичными силам тяготения. Движение тел под действием сил инерции сходно с движением в гравитационном поле. В качестве примера можно привести невесомость, возникающую в свободно падающем лифте. В свободно падающем лифте вес тела массой m всегда равен нулю: .

Читайте также: