Работа в поле тяготения кратко

Обновлено: 02.07.2024

Определим работу, совершаемую силами поля тяготения при перемещении в нем материальной точки массой . При перемещении этого поля на расстояние совершается работа (рис. 5.2):

При перемещении тела с расстояния до работа вычисляется по формуле:

Так как , то получим:

Величина, равная отношению потенциальной энергии к массе тела, является энергетической характеристикой и называется потенциалом: .

Потенциалом поля тяготения () называется скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность.

Если в последнюю формулу подставить выражение для потенциальной энергии и значение массы, равное 1, получим:

Связь между потенциалом () и напряженностью поля описывается выражением , то есть напряженность поля характеризует уменьшение потенциала на единицу длины. В векторной форме напряженность поля:

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

В чём выражается гравитационное взаимодействие тел?
Как доказать наличие взаимодействия Земли и, например, учебника физики?

Как известно, сила тяжести — консервативная сила. Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила.

Напомним, что работа консервативной силы по замкнутому контуру равна нулю.

Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения

где G — гравитационная постоянная,
М — масса Земли,
r — расстояние, на котором находится тело от центра Земли.

Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА'В'В; 3) по кривой АСВ (рис. 5.15)

1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δr_i = r_{i + 1} — r_i. Среднее значение силы тяготения равно:

Чем меньше Δri, тем более справедливо написанное выражение r 2 _сpi = r_ir_{i + 1}.

Тогда работу силы F_сpi, на малом перемещении Δr_i, можно записать в виде

Суммарная работа силы тяготения при перемещении тела из точки А в точку В равна:

2. При движении тела по траектории АА'В'В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА' и В'В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31).

3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δs_i равна ΔА_i = F_срiΔs_icosα_i.

Из рисунка видно, что Δs_icosα_i = - Δr_i, и суммарная работа опять же будет определяться по формуле (5.31).

Итак, можно сделать вывод, что А₁ = А₂ = А₃, т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА'В'ВА равна нулю.

Сила тяготения — консервативная сила.

Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком:

Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. Е_пВ = 0 при r_В → ∞, то следовательно,

Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:

Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид

где υ₁ — скорость тела на расстоянии r₁ от центра Земли, υ₂ — скорость тела на расстоянии r₂ от центра Земли.

Определим, какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.

Минимальную скорость, при которой тело в отсутствие сопротивления воздуха может удалиться за пределы сил земного притяжения, называют второй космической скоростью для Земли.

На тело со стороны Земли действует сила тяготения, которая зависит от расстояния центра масс этого тела до центра масс Земли. Поскольку неконсервативных сил нет, полная механическая энергия тела сохраняется. Внутренняя потенциальная энергия тела остаётся постоянной, так как оно не деформируется. Согласно закону сохранения механической энергии

На поверхности Земли тело обладает и кинетической, и потенциальной энергией:

где υ_II — вторая космическая скорость, М₃ и Я₃ — соответственно масса и радиус Земли.

В бесконечно удаленной точке, т. е. при r → ∞, потенциальная энергия тела равна нулю (W_п = 0), а так как нас интересует минимальная скорость, то и кинетическая энергия также должна быть равна нулю: W_к = 0.

Из закона сохранения энергии следует:

Эту скорость можно выразить через ускорение свободного падения вблизи поверхности Земли (при расчётах, как правило, этим выражением пользоваться удобнее). Поскольку то GM₃ = gR 2 ₃.

Следовательно, искомая скорость

Точно такую же скорость приобрело бы тело, упавшее на Землю с бесконечно большой высоты, если бы не было сопротивления воздуха. Заметим, что вторая космическая скорость в раза больше, чем первая.

Законы сохранения в механике - Физика, учебник для 10 класса - Класс!ная физика

Рассмотрим, чему равна работа, совершаемая силами поля тяготения при перемещении в нем материальной точки массой т. Вычислим, например, какую надо затратить работу для удаления тела массой т от Земли. На расстоянии R (рис.39) на данное тело действует сила

При перемещении этого тела на расстояние dR затрачивается работа

Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис.39).

Если тело перемещать с расстояния до , то затрачивается работа

Из формулы (25.2) вытекает, что затраченная работа в поле тяготения не зависит от траектории перемещения, а определяется лишь начальным и конечным положениями тела, т. е. силы тяготения действительно консервативны, а поле тяготения является потенциальным (см. § 12).

Согласно формуле (12.2), работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т. е.

Из формулы (25.2) получаем

Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при равной нулю ( ). Тогда (25.3) запишется в виде . А так как первая точка была выбрана произвольно, то можно записать

являющуюся энергетической характеристикой поля тяготения, называют потенциалом.Потенциал поля тяготения — скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен

где R — расстояние от этого тела до рассматриваемой точки.

Из формулы (25.4) вытекает, что геометрическое место точек с одинаковым потенциалом образует сферическую поверхность (R=const). Такие поверхности, для которых потенциал постоянен, называютсяэквипотенциальными.

Рассмотрим взаимосвязь между потенциалом поля тяготения ( ) и его напряженностью (g). Из выражений (25.1) и (25.4) следует, что элементарная работа dA, совершаемая силами поля при малом перемещении тела массой т, равна

С другой стороны, ( — элементарное перемещение). Учитывая (24.1), получим, что

Величина характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения. Можно показать, что

где - градиент скаляра (см. (12.5)). Знак минус в формуле (25.5) указывает, что вектор напряженности g направлен е сторону убывания потенциала.

В качестве частного примера, исходя из представлений теории тяготения, рассмотрим потенциальную энергию тела, находящегося на высоте h относительно Земли:

где R₀ — радиус Земли.

то, учитывая условие h

При перемещении этого тела на расстояние dR затрачивается работа

Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис.39).

Если тело перемещать с расстояния до , то затрачивается работа

Из формулы (25.2) получаем

где R — расстояние от этого тела до рассматриваемой точки.

С другой стороны, ( — элементарное перемещение). Учитывая (24.1), получим, что

Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс.

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

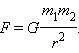
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной:

G = 6,67·10–11 Н·м2/кг2 (СИ)

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.

Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна

где g – ускорение свободного падения у поверхности Земли:

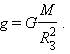
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли М:

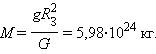
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли.

работа силы тяготения не зависит от траектории движения тела, а зависит только от положения в этом поле начальной и конечной точек перемещения тела. Силы, обладающие подобным свойством, называют консервативными, а поле таких сил - потенциальным. Следовательно, поле тяготения является потенциальным полем, а сила тяготения - консервативной силой. Расчет показывает, что работа силы тяготения А в поле тяго-тения Земли определяется по формуле. A=GMm(1/r1-1/r2), где m - масса тела; M - масса Земли; r1 и r2 - расстояния от центра Земли до начальной и конечной точек перемещения тела.

U = – GMm/r — потенциальная энергия гравитационного притяжения двух точечных масс m и M. За начало отсчета выбрана бесконечно удаленная точка.

Закон Гука. Работа силы упругости. Энергия сжатой пружины.

Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь F сила натяжения стержня, Δl — его удлинение(сжатие), а k называется коэффициентом упругости (или жёсткостью). Минус в уравнении указывает на то, что сила натяжения всегда направлена в сторону, противоположную деформации.

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как

Величина E называется модулем Юнга и зависит только от свойств тела.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука запишется как

В такой форме он справедлив для любых малых объёмов вещества.

Работа силы упругости

Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, вычислим работу, которую совершает пружина при перемещении груза.

На рисунке (а) показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой F1. направленной к положению равновесия шара, в которой пружина не деформирована. Начальное удлинение пружины равно Δl1. Вычислим работу силы упругости при перемещении шара из точки с координатой х1 в точку с координатой х2. Из рисунка (в) видно, что модуль перемещения равен:

где Δl2 - конечное удлинение пружины.

Вычислить работу силы упругости по формуле A=F*S*cos(α) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы воспользуемся графиком зависимости модуля силы упругости от координаты шара. Разобьем отрезок ВМ на столь малые элементы Δх, чтобы силу на каждом из них можнобыли считать постоянной. Используя затем прием, который применялся для вывода формулы зависимости координат от времени при движении с постоянным ускорением, можно доказать, что работа силы упругости при перемещении |Δr|=x1-x2 численно равна площади трапеции BCDM. Следовательно,

Согласно закону Гука F1=k*Δl1 и F2=k*Δl2. Подставив эти выражения в формулу, и учитывая, что |Δr|=Δl1-Δl2 получим:

Мы рассмотрели случай, когда направления силы упругости и перемещения совпадали. Можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а так же при перемещении тела вдоль кривой произвольной формы.

Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле, что вывели выше. Работа сил упругости зависит лишь от деформаций пружины Δl1 и Δl2 в начальном и конечном состоянии.

Энергия сжатой пружины -

Читайте также: