Приведите пример решения геометрической задачи с применением метода координат кратко

Обновлено: 02.07.2024

Сущность координатного метода для решения геометрических задач

Координатный метод решения задач основан на решении задач с помощью введения в задачу системы координат. В этой статье мы не будем делать акцент на том, как именно вводятся координаты, предполагая, что с этим понятием мы уже знакомы.

Метод координат для решения геометрических задач основан на следующих основных утверждениях.

Утверждение 1: Координаты вектора равны разности соответствующих координат конца вектора и его начала.

Утверждение 2: Координата середины отрезка равна полусумме соответствующих координат его концов.

Утверждение 3: Длина вектора с координатами $\left\$ равняется

Утверждение 4: Расстояние между двумя точками с координатами $\left\$ и $\$ равняется

Общая схема для решения геометрических задач координатным методом

При решении геометрических задач координатным методом рекомендуется пользоваться следующей схемой:

Провести анализ условия задачи:

а) Выяснить в какой системе координат (двумерной или трехмерной) рассматривается данная задача;

б) Записать, что нам дано, что нужно найти или доказать, а также построить чертеж по условию задачи.

Перевести условие задачи к координатам в выбранной системе координат.

Составить соотношения, соответствующие тому, что дано в задаче и привести их к соотношениям, соответствующим требованиям задачи.

Перевести полученный результат на геометрический язык.

Примеры типов задач, которые решаются векторным методом

Приведем теперь примеры простейших задач, решаемых с помощью координатного метода (Не приводя их решений).

Вычисление координат вектора по координатам его начала и конца.

Задачи о делении отрезка в данном отношении.

Задачи на доказательство принадлежности трех точек одной прямой.

Задачи на доказательство принадлежности четырех точек одной плоскости.

Вычисление расстояние между двумя точками.

Задачи на вычисление площадей и объемов геометрических фигур.

Готовые работы на аналогичную тему

Некоторые из результатов этих задач приведены нами выше в качестве основных утверждений, используемых при решении геометрических задач координатным методом.

Примеры задач на применение векторного метода

Доказать, что середина гипотенузы прямоугольного треугольника равноудалена от всех вершин этого треугольника.

Решение.

Пусть нам дан треугольник $ABC$ с прямым углом $C$. $M$ - центр гипотенузы $AB$. Введем систему координат следующим образом (рис. 1).

Введем следующие координаты по данной системе координат:

Используя утверждение 2, получим:

Найдем расстояния от этой точки до каждой из вершин, используя утверждение 4:

Доказать, что сумма квадратов всех сторон произвольного параллелограмма равняется сумме квадратов его диагоналей.

Решение.

Пусть нам дан параллелограмм $ABCD$. Введем систему координат следующим образом (рис. 2).

Основным способом решения задач по стереометрии является метод координат. Освоив его, найти угол между поверхностями или прямыми, расстояние от точки до линии, то есть фактически определить положение объекта не составит труда. Главное достоинство применения этого способа заключается в избавлении от наглядности представления сложных пространственных фигур, что позволяет понять решение даже студенту со слабой математической подготовкой.

Координаты на прямой
Расположение на плоскости
Скалярное произведение
Основные формулы
Нахождение угла
Вычисление площади и высоты
Расчёт на онлайн-калькуляторе

Координаты на прямой

Исследование свойств геометрических тел привело к возникновению отдельной науки — аналитической геометрии. Основополагающим открытием, позволяющим решать задачи, связанные с фигурами, стал координатный метод. В математике принято под координатами понимать положение точки на линии, поверхности или пространстве.

Особенностью способа является нахождение геометрических тел уравнениями. Такой подход позволяет исследовать фигуры и решать задания, взяв за основу алгебраические формулы.

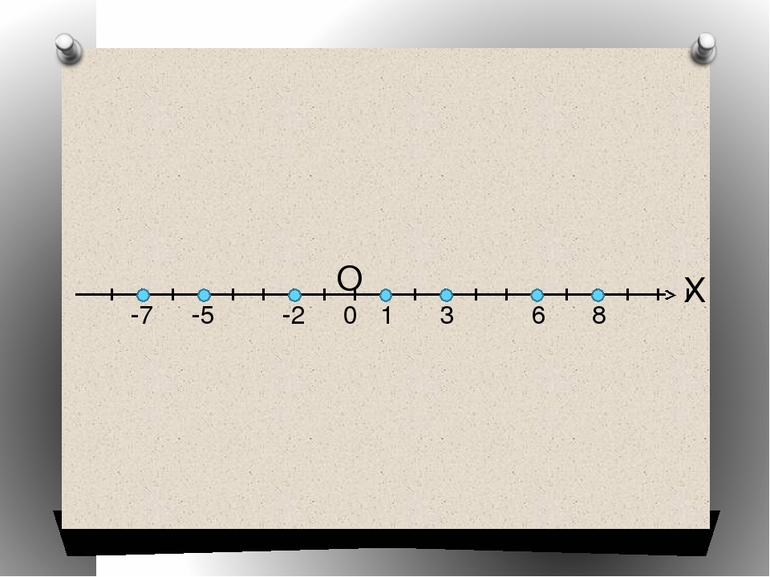
Самая элементарная задача, дающая возможность разобраться в сути, связана с определением положения точки на прямой. Пусть на линии указаны две произвольные точки A и B. Отрезок, который они ограничивают, принимают за единицу длины. Каждой точке P, входящей в AB, соответствует величина, называемая координатой.

Принимать она может три значения:

Положительное. Если P находится на отрезке AP и лежит по ту же сторону от A, что и точка B.
Отрицательное. Если P принадлежит отрезку AP, но при этом точки P и B находятся по разные стороны от B.
Нулевое. Значение координаты точки A равняется нулю.

При выполнении этих условий отрезок называют числовой осью, а A — началом координат. Любая точка, располагающаяся на прямой, имеет свою координату, отличную от других. Но при этом каждое действительное число указывает на расположение точки на рассматриваемой числовой оси. Например, запись вида A (2), B (-¾) обозначает, что числа в скобках являются координатами соответствующих точек.

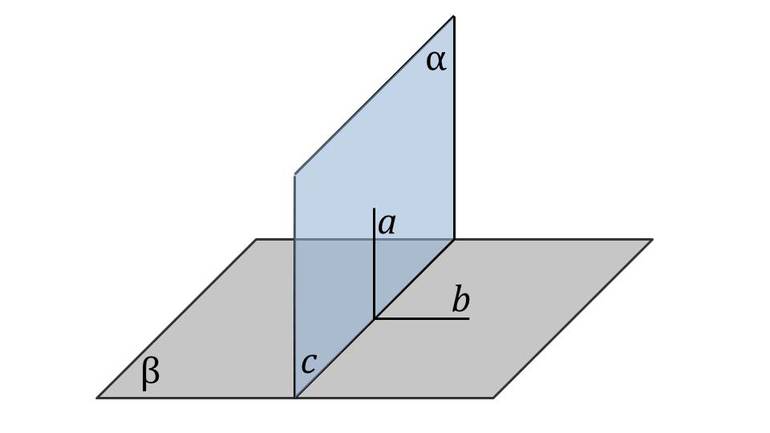
Расположение на плоскости

Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Скалярное произведение

Пусть есть два вектора a и b с известными координатами (x1, y1) и (x2, y2). Формула для выражения скалярного произведения векторов через координаты будет иметь вид: a* b = x1*x2 + y1*y2. То есть это сумма произведений соответствующих координат.

Для доказательства следует отложить два вектора из одной точки, направленные в разные стороны. Соединив их конечные точки, можно утверждать, что полученный вектор будет равняться разности a и b. Для образованного треугольника выполняется теорема косинусов: AB 2 = OA 2 + OB 2 — 2*OA*OB * cosα. Так как AB — это всё равно, что длина вектора по модулю в квадрате, то вместо AB можно написать вектор, равный a-b.

В итоге получится: |a-b| 2 = |a| 2 + |b| 2 — 2 |a|*|b|*cosα. Последнее перемножение на косинус по определению является скалярным произведением a и b. Выразив его из выражения, справедливо будет записать: a*b = (|a| 2 + |b| 2 — |a — b| 2 ) /2. Подставив координаты в формулу, получим следующее: a*b = (x1 2 + y1 2 + x2 2 + y2 2 — (x1-x2) 2 + (y1-y2) 2 ) /2 = x1*x2 + y1*y2. Равенство доказано.

Основные формулы

Зачастую в задачах, касающихся расчёта фигур, необходимо посчитать величину отрезка, лежащего на плоскости. Например, это может быть высота, медиана, биссектриса, радиус или сторона. Основной формулой считается выражение, позволяющее найти расстояние между двумя точками. Если даны две координаты A (x1, y1) и B (x2, y2), то искомое значение определяется по формуле: P (A, B) = ((x2-x1) 2 + (y2-y1) 2 ) ½ .

Если же начало отрезка лежит в нулевой точке, то выражение для вычисления его длины упрощается до вида: P (A, B) = ((x) 2 + (y) 2 ) ½ , то есть нахождения суммы квадратов чисел, определяющих координаты. Фактически это теорема Пифагора, изучаемая в шестом классе общеобразовательной школы.

Кроме нахождения длины отрезка, к основным формулам относят:

Деление отрезков в заданном отношении. Координату C (xc, yc), образованную из A (x1, y1) и B (x2, y2), определяют из соотношения: AC/CB = α1/α2, где α1,2 — действительные числа. Исходя из этого, Xc = (x1α2 + x2α1) / (α1 + α2), Yc = (y1α2 + y2α1) / (α1 + α2). В основе этих формул используется теорема Фалеса.
Вычисление угла между векторами. Если есть три точки на плоскости A (x1, y1), B (x2, y2), C (x3, y3), то угол между векторами находится как скалярное произведение, делённое на произведение их длин: cosγ = / |AB| * |AC|. Таким образом, если вектор AB = (x2-x1), (y2-y1), а AC (x3-x1, y3-y1), то C = ((x2-x1) * (x3-x1) + (y2-y1) * (y3-y1)) / ((x2-x1) 2 + (y2-y1) 2 ) * ((x3-x1) 2 + (y3-y1) 2 ) ½ .
Уравнение прямой. Для его составления нужна координата точки. Фиксирование положения в пространстве задаётся вектором α, которому рассматриваемая прямая перпендикулярна. Задача, по сути, сводится к написанию уравнения прямой, проходящей через точку N0 (x0, y0), перпендикулярную вектору n (A, B). Формула, удовлетворяющая заданию, имеет вид: A (x-x0) + B (y-y0) = 0. Равенство для прямой, проходящей параллельно вектору, пишется как (x-x0)/a = (y-y0)b. Уравнение же, описывающее прямую, проходящую через две точки, имеет вид: (x-x1)/(x2-x1) = (y-y1)/(y2-y1).

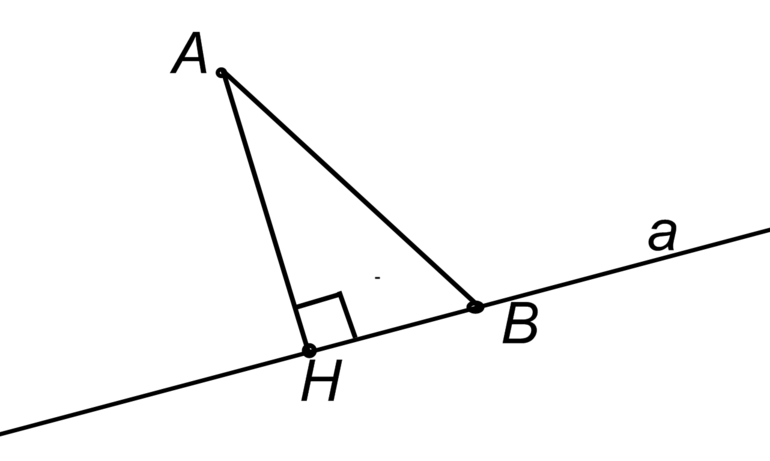
Расстояние от точки до прямой. Если имеется точка (x0, y0) и уравнение: Ax+By+C, то расстояние находится из выражения: |Ax0+Byo+C| / (A 2 +B 2 ) ½ .

Для понимания формул нужно знать о векторном и смешанном произведении векторов, а также об определителе матрицы. Зная их, можно решать задачи по вычислению элементов простейших многогранников, находить площади и объёмы.

Нахождение угла

Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:

записать уравнения плоскостей;
составить векторы нормали;
вычислить значение косинуса угла между поверхностями.

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.

Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:

Из второго равенства можно определить C. Подставив найденное C в первое равенство, можно выразить A, а после найти B. Таким образом, решением системы будет A = 0, B = -1, C = -1. Вектор нормали, соответственно, будет: N1 (0; -1; -1).

Чтобы составить уравнение второй плоскости, нужно найти координаты лишь С1. Исходя из условия, они будут равны С1 (0; 1; 1), а A и D уже известны. Подставляя данные в уравнение Ax+By+Cz+1 = 0, опять составляют систему и находят её коэффициенты. После решения второй матрицы, например, методом разложения, можно записать координаты второго вектора: N2 (-½; ½; -½).

Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2 ½ * ¾ ½ ) = 1 / (6 ½ /2) = 2/6 ½ = 6 ½ / 3. Соответственно, угол равен: α = arccos = 6 ½ / 3.

Вычисление площади и высоты

Рассмотрим типовую задачу, встречающуюся в экзаменационных работах. Даны точки с ординатами A (-2, -3); B (-3,4); C (4,5). Необходимо выполнить построение фигуры, найти её площадь и доказать, что угол A равный C.

Если отложить данные точки на плоскости и соединить их, то получится треугольник. Взяв за тождество, что углы A и C равны, можно сделать предположение о равнобедренности треугольника. Это значит, что две его стороны имеют одинаковую длину. Длина стороны AB — это отрезок A и B с заданными координатами. Поэтому равна она будет следующему выражению: AB = ((-2 + 3) 2 + (-3 — 4) 2 ) ½ = (1 +49) ½ = (50) ½ . По аналогии находится длина другой стороны: BC = ((-3 — 4) 2 + (4 — 5) 2 ) ½ = 2 = (1 +49) ½ = (50) ½ .

Таким образом, у треугольника две стороны равны, а значит, он равнобедренный. У найденных сторон общей точкой является B (вершина). Следовательно, углы A и C будут равны. Что и требовалось доказать.

Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.

В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).

Высота находится как корень квадратный из двух точек: BH = ((-3−1) 2 + (4−1) 2 ) ½ = (16+9) ½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4) 2 + (-3−5) 2 ) ½ = (36 + 64) ½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.

Расчёт на онлайн-калькуляторе

Существуют сервисы, позволяющие решать геометрические задачи координатным методом без утомительных самостоятельных вычислений. Сам расчёт обычно занимает не более трёх секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться услугами таких сайтов сможет любой пользователь интернета, даже не имеющий представления о геометрии. Всё, что от него требуется — это подключение к сети и веб-обозреватель с поддержкой Flash-технологии.

Вложение	Размер
Исследовательская работа	520.01 КБ

Предварительный просмотр:

В основе этого метода лежит так называемый метод координат, впервые применённый Декартом. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Это дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств.

В школьном курсе математики вводятся и изучаются вектор и метод координат, потребности учебного процесса требуют, чтобы ученики знали и умели решать простейшие задачи, связанные с этими понятиями на уроках физики, математики, географии. Поэтому повышенное внимание к данной теме оправдано.

Чтобы освоить определённый набор приёмов векторного и координатного методов решения геометрических задач и уметь применять их при решении задач необходимо знать теорию, провести подробный анализ условия задачи и применить имеющиеся знания к решению той или иной задачи.

раскрыть содержание метода, рассказать основные формулы и теоремы,
показать применение метода при решении конкретных задач,
решить сложные стереометрические задачи с использованием координатно-векторного метода.

изучить основы аналитической геометрии.
исследовать и изучить типичные задачи, встречающиеся на итоговой аттестации.
анализ различных методов решения задачи: координатно-векторный метод, геометрический с применением теорем;
сравнение преимуществ и недостатков каждого метода.

Предмет исследования – применение координатно-векторного метода к решению стереометрических задач.

Методы и приёмы исследования:

поиск, анализ и синтез различных источников информации: книг, статей, Интернет-ресурсов;
самостоятельное решение задач и геометрическим, и координатно-векторным способами;
сравнение двух решений одной задачи и выявление более рационального.

1.1. Декартовы прямоугольные координаты в пространстве.

Декартова прямоугольная система координат в пространстве определяется заданием линейной единицы для измерения длин и трёх пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в каком-либо порядке.

Точка пересечения осей называется началом координат, а сами оси — осями координат. Первая координатная ось называется осью абсцисс, вторая — осью ординат, третья — осью аппликат.

Начало координат обозначается буквой О, оси координат обозначаются соответственно символами Ох, Оу, Оz.

Пусть М — произвольная точка пространства, М х , Му и М г — её проекции на координатные оси (рис. 1).

Координатами точки М в заданной системе называются числа:

х = ОМ х , у = ОМ у , z = ОМ г ,

где ОМ Х есть величина отрезка оси абсцисс, ОМ у — величина отрезка оси ординат, ОМ z — величина отрезка оси аппликат. Число х называется абсциссой, у — ординатой, z — аппликатой точки М. Символ М (х; у; z) обозначает, что точка М имеет координаты х, у, z.

Три плоскости Оху, Охz и Оуz вместе разделяют пространство на восемь частей; их называют координатными октантами и нумеруют так, как показано на рис. 2.

1.2. Расстояние между двумя точками. Деление отрезка в данном отношении.

Расстояние d между двумя точками M 1 (x 1 ; у 1 ; z 1 ) и M 2 (x 2 ; y 2 ; z 2 ) в пространстве определяется формулой

Координаты х, у, z точки М, которая делит отрезок , ограниченный точками M 1 (х 1 , y 1 , z 1 ) и M 2 ( x 2 ; y 2 ; z 2 ), в отношении , определяются по формулам:

, ,

В частности, при λ = 1 имеем координаты середины данного отрезка:

, , .

1.3. Скалярное произведение векторов.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Если угол между векторами а , b обозначить через , то их скалярное произведение можно выразить формулой . (1)

Из формулы (1) следует, что ab > 0, если — острый угол, ab — тупой; ab = 0 в том и только в том случае, когда векторы a и b перпендикулярны (в частности, a = 0, если a = 0 или b = 0).

Если векторы а и b заданы своими координатами:

, и ,

то их скалярное произведение может быть вычислено по формуле

Отсюда следует необходимое и достаточное условие перпендикулярности векторов:

Угол между векторами и

даётся формулой , или в координатах,

Применение метода координат удобно при решении геометрических задач. Процесс решения каждой задачи, решаемой с помощью метода координат, условно разбивают на три этапа:

В кубе ABCDA 1 B1C1D1 с ребром 1 точка О – центр грани ABCD. Найти угол между прямыми A 1 D и B 1 O.

1 способ. Координатно-векторный метод

Поместим наш куб в прямоугольную систему координат как показано на рисунке, таким образом, что вершина Е лежит в начале системы координат, тогда вершины A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0).

Направляющие векторы прямых A 1 D и B 1 O: и ; искомый угол φ между ними находим по формуле:

cos ∠ φ = = = ,

2 способ. Геометрический

Проведем прямую В 1 С параллельно прямой A 1 D. Угол CB 1 O будет искомым.

В основании квадрат АВСD, из треугольника DВС по теореме Пифагора найдем DВ

DВ = = , тогда ВO = .

2) Из прямоугольного треугольника BB 1 O по теореме Пифагора:

B 1 O = .

3) Из прямоугольного треугольника CB 1 O найдём угол CB 1 O:

данный угол составляет 30°,так как напротив него лежит катет OC равный половине гипотенузы B 1 C.

На ребрах AD и ВВ 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 , у которого АВ:AD:АА 1 = 1:2:2, взяты соответственно точки E и F – середины этих ребер. Найдите угол, который образует прямая EF с прямой АС 1 .

1 способ. Координатно-векторный метод

Введем систему координат с началом в точке А, ось Ох направим по AD, ось Оу –по AB, ось Оz – по .

Определим координаты всех вершин параллелепипеда.

По условию АВ: АD: АА 1 = 1:2:2

АВ= а, АD=2а, АА 1 =2а.

А 1 (0;0;2а); С 1 (2а;а;2а); F(0;a;a).

(-а; а; а) (2а;а;2а).

EF и АС 1 скрещивающиеся,

cos

2 способ. Геометрический

Построим прямую ЕС 2 ║ АС 1 , таким образом, что С 2 лежит на продолжении прямой В 1 С 1 за точку С 1 . Так как АЕ = х, то и С 1 С 2 = х. Прямая ЕС 2 пересекает ДС 1 в точке М, которая является серединой ДС 1, так как ЕМ – средняя линия треугольника АDС 1 .

Угол FЕМ – искомый.

Из треугольника DСС 1 найдем по теореме Пифагора ДС 1 = = х , так как М середина ДС 1 , то ДС 1 = . Из прямоугольного треугольника ЕDМ: ЕМ = . Из треугольника АВF: АF= х . Из треугольника АЕF: ЕF = х .

$C:\Documents and Settings\Админ\Local Settings\Temporary Internet Files\Content.Word\Фото125.jpg$

Точка F середина ВВ 1 , точка М середина ДС 1 , тогда FМ= В 1 N = = .

Из треугольника ЕFМ по теореме косинусов найду косинус угла ЕFМ: = .

Ответ: .

В основании пирамиды МАВС лежит равнобедренный треугольник с прямым углом при вершине С. Каждое боковое ребро пирамиды наклонено к плоскости основания под углом 45 о . На ребре МС взята точка F – середина этого ребра. Найдите угол, который образует прямая AF с плоскостью МОС, точка О – середина ребра АВ.

1 способ. Координатно-векторный метод

Найдем (AF;(MOC))= .

Ведем систему координат Оxyz так, чтобы точка О совпала с началом координат, М OZ;

CO- медиана и высота АВС. Все боковые ребра равно наклонены к основанию, потом М проектируется в центр описанной около АВС окружности, то есть в середину гипотенузы О, АО=ОВ=ОС; С Ох; В Оу.

Пусть АС = СВ = а, тогда АВ= ; О(0;0;0) В(0; ;0) А(0; ;0) С( ;0;0).

ОМ= ОС, т.к ОМС равнобедренный прямоугольный. М(0;0; )

FK|| OM, FK OC; FK средняя линия CMO, FK= ;

, OF .

Угол АFО – искомый.

cos

cos АFO = = = .

2 способ. Геометрический

AF =F

CO-медиана и высота Δ ACB; CO ⊥ AB; O-медиана и высота Δ MAB; MO ⊥ AB AB ⊥ (MOC) (признак перпендикулярности прямой и плоскости).

AO ⊥ (MOC), O AB; AF-проекция наклонной AF на плоскость MOC.

Δ AFO прямоугольный, ∠ AFO=90 ° , AO ⊥ (MOC),FO (MOC) AO ⊥ FO.

Sin AFO= ; AO= AB= ; MO=OB=

MB =MO +OB = + . MB=a

MA=MB=MC=AC=a Δ AMC-равносторонний AF-медиана и высота Δ AMC

AF =AC -CF =a - = ; АF =

sin AFO = , cos АFO .

Ответ: .

В правильной треугольной призме, все ребра которой равны 1, найдите косинус угла между прямыми АВ и А 1 С.

1 способ. Координатно-векторный метод

Поместим призму в декартову систему координат, таким образом, что бы АС лежал на оси абсцисс, и точка С(0; 0; 0). Тогда координаты точки А(1; 0; 0), А 1 (1; 0; 1).

$C:\Documents and Settings\Админ\Local Settings\Temporary Internet Files\Content.Word\Фото123.jpg$

Найдем координаты точки В. В треугольнике АСВ опустим из точки В перпендикуляр ВН на АС. ВН = = .

СА 1 , ВА < ; ; 0>. = = = .

2 способ. Геометрический

Построим СN параллельно АВ, таким образом, что СN = АВ, тогда АВСN – ромб. Угол А 1 СN – искомый.

$C:\Documents and Settings\Админ\Local Settings\Temporary Internet Files\Content.Word\Фото123.jpg$

Из треугольника АА 1 С найдем А 1 С: А 1 С = = .

Δ NАА 1 = ΔС АА 1 по трем сторонам, значит NА 1 = СА 1 = .

По теореме косинусов из треугольника NА 1 С найдем искомый угол:

= = = . Ответ : .

В правильной четырехугольной пирамиде ВСD длины стороны основания и высоты соответственно равны 1 и 2. Найти расстояние между прямыми BD и SA.

1 способ. Координатно-векторный метод

Введем прямоугольную систему координат, поместив начало координат в вершину А основания пирамиды и направив оси координат так, как показано на рисунке. Тогда вершины пирамиды будут иметь координаты А(0; 0; 0), В(1; 0; 0), D(0; 1; 0), S ( ; ; 2) и соответственно координаты векторов: , В, ВD. Общий перпендикуляр к прямым AS и BD обозначим EF.

EF= EА + АВ + ВF=k*SА + АВ + m* ВD. Коэффициенты k и m найдем из условий EF ⊥ ВD и EF ⊥ SА. Векторы перпендикулярны, если их скалярное произведение равно нулю.

Тогда EF < > и = = .

2 способ. Геометрический

Прямые AS и BD скрещивающиеся. Расстояние между одной из скрещивающихся прямых и плоскостью проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

Произведем соответствующие построения: АС перпендикулярна ВD, так как в основании квадрат. EF – наклонная к плоскости основания и перпендикуляр к AS, по теореме о трех перпендикулярах EF перпендикулярна ВD. Значит EF- искомое расстояние.

Треугольник А С равнобедренный, высота пирамиды, EF – перпендикуляр к AS и BD. Из прямоугольного треугольника АВС найдем АС по теореме Пифагора: АС = . Так как

F – середина АС, то EF = . Из прямоугольного треугольника ASF: AS= = , = = . Из треугольника АEF: EF = * АF = = .

Ответ: .

Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:

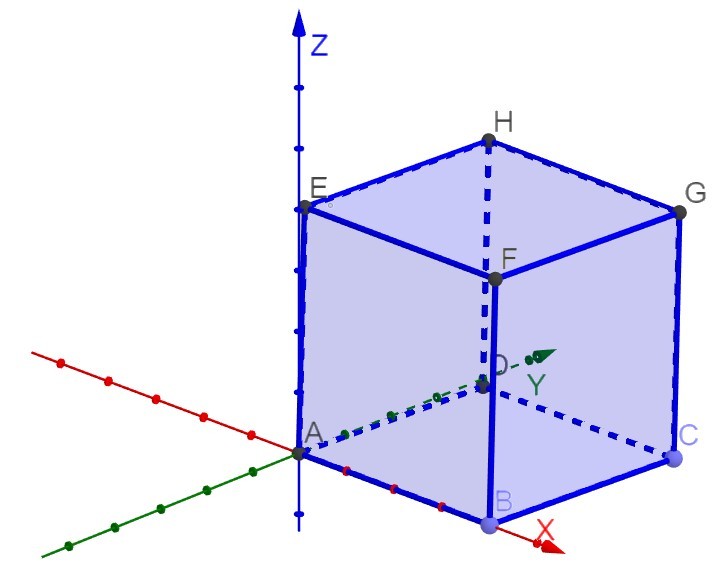
Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны $4$):

Куб: Очевидно, что координаты точки $A$ в начале координат - $(0;0;0)$. т. $B$ - $(4;0;0)$, т. $G$ - $(4;4;4)$ и т.д. (Рис. 1).

С кубом все просто, но в других фигурах могут возникнуть трудности с нахождением координат.

У $т. A$ координаты $(0;0;0)$, потому что она лежит в начале координат.

Координату $x$ точки $С$ можно получить, опустив перпендикуляр $CE$ из $т.С$ на ось $OX$. (см. Рис. 2). Получится $т.E$, указывающая на искомую координату по $x$ – 2.

Координату $y$ точки $С$ тоже получаем, опустив перпендикуляр $CF$ на ось $OY$. Координата $y$ $т.С$ будет равна длине отрезка $AF=CE$. Найдем его по теореме Пифагора из треугольника $AFC$: $$ ^2=^2+^2,$$ $$ 4^2=2^2+^2,$$ $$ CE=\sqrt. $$ Координата $z$ точки $C$, очевидно, равна $0$, потому что $т.С$ лежит в плоскости $XOY$. $$ C (2;\sqrt; 0). $$

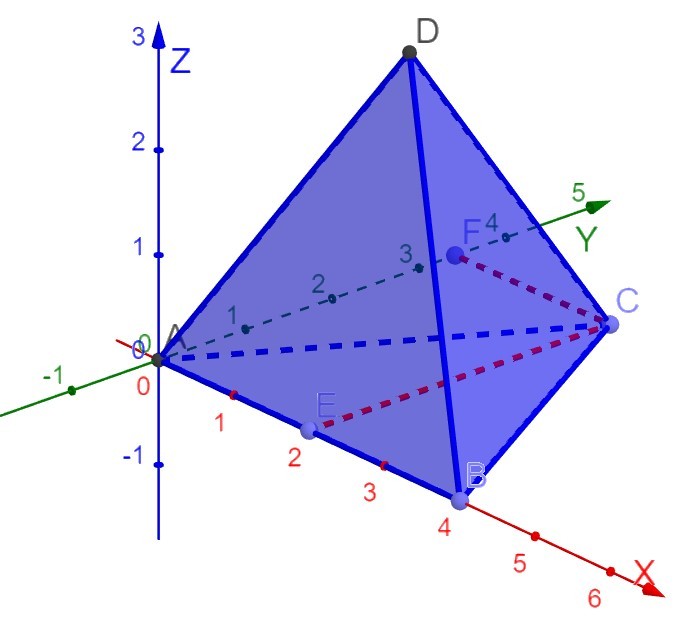
И найдем координаты вершины пирамиды ($т.D$). (Рис. 3) Координаты $X$ и $Y$ у точки $D$ совпадают с координатами $X$ и $Y$ у точки $H$. Напомню, что высота правильной треугольной пирамиды падает в точку пересечения медиан, биссектрис и высот. Отрезок $EH=\frac*CE=\frac*\sqrt$ (медианы в треугольнике точкой пересечения делятся в отношении как $\frac$) и равен координате точки $D$ по $Y$. Длина отрезка $IH=2$ будет равна координате точки $D$ по $X$. А координата по оси $Z$ равна высоте пирамиде: $$ ^2=^2+^2, $$ $$ =\sqrt*AF>^2>, $$ $$ =\frac. $$ $$ D (2, \frac*\sqrt, \frac). $$

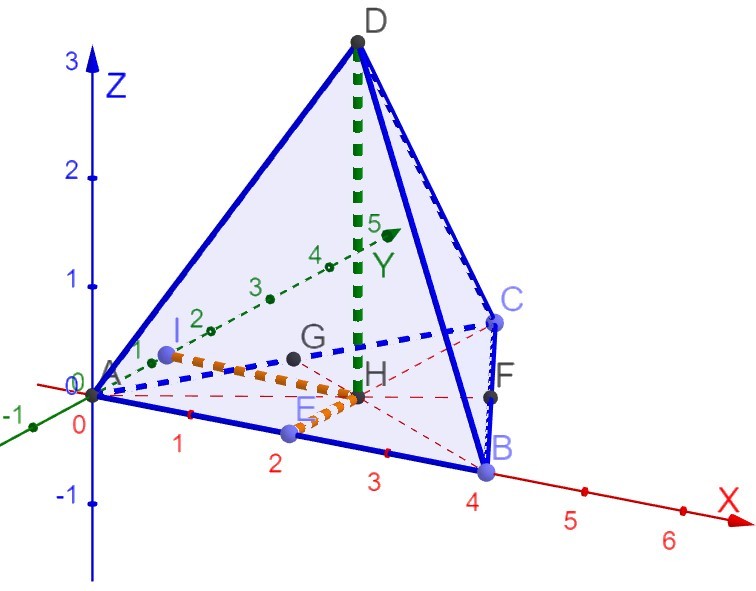
Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

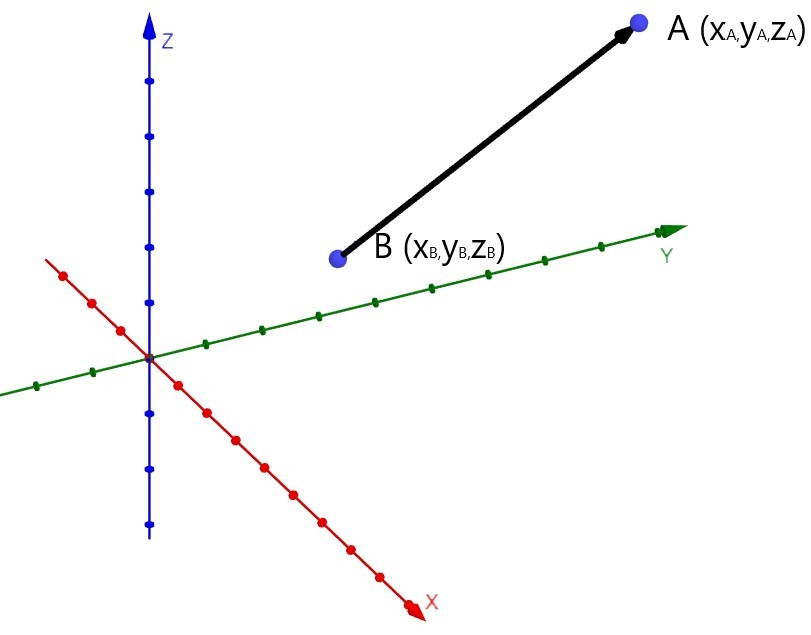
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) : $$ т.А(x_A,y_A,z_A); $$ $$ т.B(x_B,y_B,z_B); $$ Тогда координаты вектора $\vec$ можно определить по формуле: $$ \vec=. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора: $$ a=;$$ $$ b=; $$ тогда угол $\alpha$ между ними находится по формуле: $$ \cos=\frac^2+^2+^2>*\sqrt^2+^2+^2>>. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой: $$ A*x+B*y+C*z+D=0,$$ где $A,B,C,D$ – какие-то числа.

Если найти $A,B,C,D$, то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

$$\begin A*x_K+B*y_K+C*z_K+D=0,\\ A*x_L+B*y_L+C*z_L+D=0, \\ A*x_P+B*y_P+C*z_P+D=0.\end$$

Получилась система из трех уравнений, но неизвестных 4: $A,B,C,D$. Если наша плоскость не проходит через начало координат, то мы можем $D$ приравнять $1$, если же проходит, то $D=0$. Объяснение этому простое: вы можете поделить каждое ваше уравнения на $D$, от этого уравнение не изменится, но вместо $D$ будет стоять $1$, а остальные коэффициенты будут в $D$ раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Найти уравнение плоскости, проходящей через точки $$ K(1;2;3);\,P(0;1;0);\,L(1;1;1). $$ Подставим координаты точек в уравнение плоскости $D=1$: $$\begin A*1+B*2+C*3+1=0,\\ A*0+B*1+C*0+1=0, \\ A*1+B*1+C*1+1=0.\end$$ $$\begin A+2*B+3*C+1=0,\\ B+1=0, \\ A+B+C+1=0.\end$$ $$\begin A-2+3*C+1=0,\\ B=-1, \\ A=-C.\end$$ $$\begin A=-0.5,\\ B=-1, \\ C=0.5.\end$$ Получаем искомое уравнение плоскости: $$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

Зная координаты некоторой точки $M(x_M;y_M;z_M)$, легко найти расстояние до плоскости $Ax+By+Cz+D=0:$ $$ \rho=\frac<|A*x_M+B*y_M+C*z_M+D|>>. $$

Найдите расстояние от т. $H (1;2;0)$ до плоскости, заданной уравнением $$ 2*x+3*y-\sqrt*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты: $$ A=2,\,B=3,\,C=-\sqrt,\,D=4.$$ Подставим их в формулу для нахождения расстояния от точки до плоскости. $$ \rho=\frac<|2*1+3*2-\sqrt*0+4|><\sqrt<2^2+3^2+<-\sqrt>^2>>. $$ $$ \rho=\frac>=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Читайте также: