Принцип ферма в оптике кратко
Обновлено: 08.07.2024
До сих пор мы рассматривали все соотношения геометрической оптики и законы действия оптических инструментов как следствие основных законов отражения и преломления света, сформулированных в § 8.
Однако, как показал около 300 лет назад Ферма, эти основные законы могут быть в свою очередь выведены из одного более общего принципа. Принцип Ферма утверждает, что свет распространяется по такому пути, при котором время, необходимое для прохождения света от одной точки до другой, имеет наименьшее или наибольшее значение (экстремум) 1).
Если тело имеет показатель преломления то скорость света этом теле равна где с — скорость света в пустоте. Поэтому
время, в течение которого свет проходит расстояние I в среде с показателем преломления определяется соотношением
Произведение геометрического пути I на показатель преломления называют оптическим путем. Пусть свет проходит несколько сред с показателями преломления (рис. 39). Из точки А свет попадает в В по такому пути для которого время
имеет наибольшее или наименьшее значение.
Так как скорость света с в пустоте есть величина постоянная, то можно сформулировать принцип Ферма так: между точками оптический путь имеет минимальное или максимальное значение.
Из принципа Ферма легко вывести законы отражения и преломления.
Рис. 39. К принципу Ферма,
Рис. 40. Закон отражения как следствие принципа Ферма
В случае отражения оптический путь пропорционален геометрическому пути, так как распространение света происходит в одной среде. Поэтому применение принципа Ферма к отражению света сводится к решению чисто геометрических задач.
Пусть требуется найти кратчайший путь из точки при условии, что путь должен проходить через точку, лежащую на поверхности зеркала (рис. 40). Иначе говоря, требуется найти такую точку О на зеркале, чтобы путь был минимальным. Возьмем точку А, симметричную с А относительно поверхности зеркала Для любой точки отрезок следовательно, Отсюда становится очевидным, что искомой точкой будет точка О, лежащая на пересечении прямой В А
с поверхностью зеркала Из этого способа построения точки О получается закон отражения:
В то время как при отражении от плоского зеркала оптический путь имеет минимальное значение, в других случаях он может быть максимальным. Так, при отражении от вогнутых зеркал имеет место как наименьший оптический путь, так и наибольший. Пусть (рис. 41) — вогнутое зеркало, две точки, между которыми нужно найти оптический путь луча, отражающегося от зеркала
Рис. 41. При отражении от кривого зеркала оптический путь имеет иногда наименьшее, а иногда наибольшее значение.
Рис. 42. Вывод закона преломления из принципа Ферма.
Построим эллипсоид вращения с фокусами касательный к поверхности Из геометрического свойства эллипса следует, что все лучи, исходящие из А, собираются в точке В. Следовательно,, искомый оптический путь проходит через точку касания Легко показать, что путь больше любого другого В самом деле, Последняя же сумма по геометрическому свойству эллипса равна Таким образом, рассмотренный случай дает пример наибольшего оптического пути. В случае вогнутого зеркала касательного к эллипсу снаружи, отражение происходит при минимальном оптическом пути, так же как в случае плоского зеркала и выпуклого
Когда свет проходит через границу (рис. 42) между двумя средами с показателями преломления то из условия минимума или максимума оптического пути
получается закон преломления:
где углы с нормалью к поверхности
Если величина имеет для светового луча экстремальное значение, то это значит, что величина при бесконечно малых изменениях формы луча не должна практически меняться. В данном случае наблюдается то же и в максимуме или минимуме обычной функции от какого-либо аргумента: бесконечно малые изменения аргумента не изменяют значения функции (производная равна нулю). Разница только в том, что величина зависит не от какого-либо аргумента, а от формы луча Проведем через точку С, бесконечно близкую к С, луч согласно сказанному длина оптического пути V для этого луча должна быть равна длине оптического пути
Проведем из А и в окружности радиусами и тогда ввиду малости можно считать, что
или, пользуясь полученным выше соотношением:
Рассматривая треугольники и как прямоугольные, получим:
Подставив эти выражения и сократив на получим:
Если рассмотреть действие любой оптической системы, дающей изображения, То на первый взгляд кажется, что мы имеем дело с резким нарушением принципа Ферма. Свет от любой точки предмета до ее изображения распространяется по бесчисленному числу различных путей. Все лучи, вышедшие из светящейся точки, собираются в ее изображении, преломляясь и отражаясь различным образом.
Однако оказывается, что и здесь все находится в полном согласии с принципом Ферма. Частным случаем экстремума какой-либо величины является постоянство этой величины. Время прохождения света по всем лучам, образующим изображение точки, будет одно и то же. Задача становится неопределенной, мы не можем выбрать луча, соответствующего минимальному или максимальному времени, и сказать, что все остальные запрещены. Все лучи, идущие через оптическую систему, равновозможны с точки зрения принципа Ферма. Как было указано, если мы поместим источник в один фокус
эллиптического зеркала, то все лучи соберутся в другом фокусе. Из геометрических свойств эллипса прямо следует, что оптический путь от одного фокуса до другого по всем лучам будет один и тот же в согласии с принципом Ферма.
При прохождении линзы (положительной) центральный луч проходит меньший геометрический путь, чем краевые лучи, но, пользуясь формулой (5), можно показать, что оптические пути всех лучей будут равны. Этот результат вполне понятен, ибо чем короче световой луч (рис. 17), тем больший путь этот луч должен пройти в стекле, где свет распространяется медленнее, чем в воздухе. Вот это замедление света в стекле и компенсирует укорочение геометрического пути луча. Можно поступить наоборот и из постоянства оптических путей получить формулу (5).
Рис. 43. Астрономическая рефракция.
Все сказанное о равенстве оптических путей, конечно, справедливо только для случаев идеального изображения, когда светящейся точке соответствует точечное изображение. Если же система не сводит всех лучей, вышедших из точки, опять в одну точку, то, естественно, нарушается постоянство оптического пути по всем лучам. Чем хуже будет качество изображения, тем сильнее будут расходиться значения для различных оптических путей. В современной теории ошибок оптических инструментов, основанной Гамильтоном, мерилом качества оптической системы служит величина отклонений от постоянства оптических путей для различных лучей.
Особенно интересны применения принципа Ферма в оптике сред с непрерывно меняющимся показателем преломления.
В случае среды с непрерывно меняющимся показателем преломления условие максимума или минимума оптического пути может быть написано как условие максимума или минимума интеграла, выражающего сумму оптических путей
где элемент геометрического пути, показатель преломления — функция координат. Путь светового луча оказывается в этом случае криволинейным. Так, например, в земной атмосфере наблюдаются явления рефракции и миража, происходящие вследствие непрерывного изменения плотности, а следовательно, и показателя преломления воздуха. Так как плотность воздуха с высотой убывает, то рефракция искривляет световой луч, идущий от звезды (рис. 43), делает его падающим на землю более
отвесно, и поэтому наблюдатель видит звезду в точке 5, находящейся выше истинного положения звезды
Миражи наблюдаются при возникновении резких изменений плотности воздуха с высотой, которые вызываются Температурными условиями. Над раскаленным песком пустыни воздух сильно нагрет и плотность его мала. Поэтому до известной высоты в таких условиях может наблюдаться рост плотности воздуха с высотой, т. е. рост показателя преломления воздуха с высотой. Такое необычное изменение показателя преломления вызывает искривление светового луча, изображенное на рис. 44, а. Световой луч своей выпуклостью обращен к Земле, а не от Земли. В этом случае наблюдателю кажется, что световые лучи исходят от перевернутого предмета или что световые лучи отражаются от плоского зеркала. Это плоское зеркало воспринимается как большая водная поверхность.
Рис. 44. Происхождение миража
Наоборот, при резком убывании плотности воздуха с высотой световые лучи искривляются, так же как и при рефракции, но в гораздо большей степени. В результате световые лучи, идущие от предметов, лежащих за горизонтом, огибают Землю и попадают в глаз наблюдателя (рис. 44, б). Наблюдатель видит далекие предметы, и они ему кажутся близкими.
Но интересно, что задолго до этого был сформулирован удивительный принцип, из которого прямо следуют все основные законы распространения света. Принцип этот, найденный французским математиком Пьером Ферма (1601-1665) около 1660 года, гласит: из всех возможных путей между двумя точками свет проходит по тому, по которому время прохождения наименьшее.
Из принципа Ферма (так его обычно называют) следует, что в однородной среде (в такой среде скорость света всюду одинакова) свет должен распространяться прямолинейно: прямая — кратчайшее расстояние между двумя точками, следовательно, и время распространения — наименьшее.
Покажем теперь, что закон отражения света — тоже прямое следствие принципа Ферма.
Закон отражения света
Пусть ММ — плоское зеркало. В точке А находится источник света, и нас интересует, по какому пути свет, отразившись от зеркала, приходит из точки А в точку В (рис. 1).

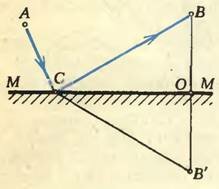
Опустим из точки В перпендикуляр на зеркало ММ и продолжим его по другую сторону зеркала до точки В’, отстоящую от зеркала на расстоянии |ОВ’| = |ОВ|. Проведем линию СВ’. Получившиеся треугольники СОВ и СОВ’ равны друг другу, так как они прямоугольные, сторона ОС у них общая и |ОВ| = |ОВ’|. Следовательно, |CВ| = |CВ’|, откуда следует, что длина пути луча АСВ равна сумме длин от А до точки С падения луча на зеркало и от этой точки до токи В. Ясно, что эта сумма будет наименьшей, если точка С будет лежать на прямой, соединяющей точки А и В’ (рис. 3).
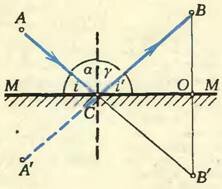
Тогда и сумма длин |АС| и |СВ|, то есть длина всего пути света, будет наименьшей, Наименьшим будет и время прохождения светом этого пути.
Из рисунка 3 видно, что ∠ ВСО = ∠ В’СО (треугольник ВСВ’ равнобедренный, поэтому СО — биссектриса угла при вершине), а ∠ В’СО = ∠ АСМ (как вертикальные). Это значит, что углы наклона падающего и отраженного лучей к зеркалу равны друг другу. В этом и состоит закон отражения света. Принято, однако, отсчитывать углы не от плоскости зеркала, а от нормали к ней в точке падения. Но ясно, что если равны углы i и i’, то равны и углы α и γ - Закон отражения обычно записывается в виде
Отметим еще одну важную особенность, связанную с отражением света от зеркала. Если в точке А (см. рис. 3) находится источник света, а в точке В — глаз, то глаз воспримет свет так, как будто бы источник света находится не в А, а в А’, а зеркала вовсе нет. Если зеркало убрать, а источник перенести из А в А’, то глаз не заметит такой замены.
Закон преломления света
Из принципа Ферма можно получить и закон преломления света (точнее — световых лучей). Здесь речь идет о переходе света из одной среды (среда I на рисунке 4) в другую (среда II) через границу раздела между ними. Различие сред состоит в том, что в них различны скорости распространения света.
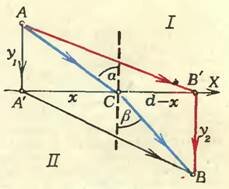
Мы рассмотрим случай, когда среда I — это вакуум, в котором скорость света равна с, а вторая среда — какое-то прозрачное вещество (например, стекло, вода и т. д.), в котором скорость света υ меньше, чем с : с > υ.
Обозначим расстояние между А’ и В’ через d. Если нужная нам точка С пересечения границы раздела находится на расстоянии х от А’, то от В’ она отстоит на расстоянии d — х (см. рис. 4). Путь АС, проходимый светом в среде I, равен \(~\sqrt\), а время прохождения этого пути
Путь СВ, проходимый светом в среде II, равен \(~\sqrt\), а время, нужное для прохождения этого пути,
Общее время t определяется равенством
Время t зависит только от х — координаты точки падения луча, так как величины y1, y2, с, υ и d — постоянные, то есть одинаковые при всех значениях х. Вот нам и нужно найти, при каком значении х время t будет наименьшим. Средствами обычной алгебры эту задачу решить нельзя. Чтобы ее решить, нужно воспользоваться тем, что при том значении х, при котором t минимально, производная функции, стоящей в правой части уравнения (1), равна нулю [1] .
Это приводит нас к такому условию для х:
Из рисунка 4 видно, что
где α — угол между падающим лучом и нормалью к границе раздела в точке падения (угол падения) и β — угол между этой нормалью и преломленным лучом (угол преломления). Условие (2) принимает поэтому вид:
В этом и заключается закон преломления для нашего случая: отношение синуса угла падения к синусу угла преломления равно отношению скоростей распространения света в вакууме и в среде, которая с ним граничит. Отношение \(~\frac<\upsilon>\) — величина постоянная, характерная для данной среды. Она называется показателем преломления вещества и обозначается буквой n, так что
В общем случае, когда свет переходит из произвольной среды, в которой скорость света равна υ1, в среду со скоростью света в ней υ2, закон преломления имеет вид
где n21 — относительный показатель преломления сред 2 и 1.
Принцип Ферма справедлив, конечно, не только для тех простейших примеров отражения и преломления света, которые мы здесь рассмотрели. С помощью этого принципа можно понять и точно рассчитать ход лучей и в призме, и в линзе и в любой самой сложной системе призм, линз, зеркал.
Принцип Ферма - это физический принцип , приписываемый Пьеру де Ферма , который является основой оптической геометрии. Он описывает форму оптического пути о наличии светового луча и формулируется следующим образом :
Основное следствие принципа Ферма - прямолинейное распространение световых лучей в однородных средах . В самом деле, в однородной среде время прохождения пропорционально длине пути, а кратчайший путь в евклидовом пространстве от одной точки к другой - это прямая линия .
Он позволяет найти большинство результатов геометрической оптики , в частности законы отражения на зеркалах, законы преломления , закон Снеллиуса-Декарта и т. Д.
Резюме
Исторический
"Эта природа всегда действует простейшими средствами, то есть кратчайшими путями, когда не требуется больше времени, или, во всяком случае, в кратчайшие сроки, чтобы сократить его работу и подойти к концу. операция раньше. "
В 1746 году Мопертюи использовал эквивалентный принцип финалиста, чтобы ввести принцип наименьшего действия , который позже разработали Эйлер и Лагранж .
В 1924 году Луи де Бройль идентифицировал принцип Ферма и принцип наименьшего действия, предложив, чтобы каждая массивная частица была связана с волной: это открыло путь для дуальности волна-частица, ведущего к уравнению Шредингера , фундаментальному в квантовой механике .
Стационарное или минимальное время в пути

Принцип Ферма был изложен выше в его общей форме, но должен быть изложен в более строгой форме:
Свет распространяется из одной точки в другую по таким траекториям, что продолжительность поездки остается неизменной .
Действительно, если в большинстве случаев мы встречаем пути с минимальным временем в пути, мы не должны забывать, что могут существовать и другие ситуации. Например, чтобы перейти из точки A в точку B, расположенную внутри вогнутого зеркала, показанного напротив, отражаясь от поверхности только один раз, свет может пройти два пути минимальной продолжительности (красный) и путь максимальной продолжительности (зеленый ) среди маршрутов, состоящих из двух участков AM и BM. Изучение длины пути выявило бы три локальных экстремума, два минимума и один максимум, для этого типа путешествия. В M B знак равно В M + M B
Та же проблема обнаруживается в формулировке принципа наименьшего действия , который для механики является тем же, что принцип Ферма для оптики, в определении минимальных поверхностей (которые не обязательно . минимальны) или в определении геодезических .
Формулировка принципа Ферма с использованием оптического пути
Случай однородной среды
Оптический путь света , чтобы перейти от точки к точке в однородной среде, обозначается , определяется как число пропорционально времени , затраченному луча , чтобы перейти от к , коэффициент пропорциональности такова , что равен дистанция для курса в вакууме. Призывая к быстроте света в середине и в вакууме, мы, следовательно, имеем и , откуда ; коэффициент пропорциональности называется показателем преломления среды. Таким образом, оптический путь определяется: В B L ( В , B ) В B L ( В , B ) В B v против L ( В B ) знак равно α В B v >> α В B против знак равно В B > = AB> L ( В , B ) знак равно против v В B <\ Displaystyle L (A, B) = <\ tfrac > AB> нет знак равно против v <\ Displaystyle п = <\ tfrac >>
L ( В , B ) знак равно нет ⋅ В B
Случай любой сплошной среды
Мы рассматриваем две точки, бесконечно соседние и удаленные на расстояние . Оптический путь, разделяющий эти две точки, определяется как ; - это разность оптического пути или даже бесконечно малый унитарный элемент оптического пути. Чтобы найти оптический путь, разделяющий две точки и на этой кривой, достаточно произвести интегральную сумму всех элементов по криволинейной координате, разделенной точками и : d s s> d L знак равно нет . d s L = п. \ mathrm s> d L L> L ( В B ) В B d L L> s В B
Затем формулируется принцип Ферма:
Между двумя точками и , достигаемые светом, оптический путь, проходящий вдоль пути, является стационарным. В B
Последствия
Принцип обратного возврата света
Путь, по которому свет идет от одной точки к другой, не зависит от направления распространения света.
Стационарность оптического пути позволяет сделать некоторые соображения. Между двумя точками A и B, обе на криволинейной траектории светового луча, распространяющегося в неоднородной среде, мы можем выразить интеграл оптического пути следующим образом:
L ( В B ) знак равно ∫ В B нет d s знак равно ∫ B В нет ( - d s ) знак равно ∫ B В нет d s ′ n \, \ mathrm s = \ int _ n \, (- \ mathrm s) = \ int _ n \, \ mathrm s '>
Учитывая, что это криволинейный элемент координат от B до A, мы можем написать . В случае исследования оптической системы это означает, что мы можем изучать распространение света и путь световых лучей, не беспокоясь о направлении распространения. d s ′ знак равно - d s s '= - \ mathrm s> L ( В B ) знак равно L ( B В )
Предупреждение: на практике бездумное использование этого принципа приводит к абсурду. Мы знаем, например, что объектив никогда не дает точного изображения световой точки, а дает всегда более или менее размытое изображение. Было бы ребячеством думать, что лучи, образующие это пятно, отраженные обратно в линзу плоским зеркалом, могут преобразовать точку четкого изображения на другой стороне . Здесь идет речь не о принципе, а о факте. о желании применить это неправильно.
Законы Снеллиуса-Декарта
Плоскость вектора нормали разделяет две среды с показателями преломления и . Световой луч начинается от точки , расположенной в первой среде, пересекает в и достигает точку . Проблема состоит в том, чтобы найти положение из принципа Ферма. п нет → >> нет 1 > нет 2 > В 1 > п M В 2 > M
Эта демонстрация в основном принадлежит Мопертюи в 1744 году, почти через столетие после того, как Ферма сформулировал свой принцип.
Мы доказываем, что если разделительной поверхностью двух сред является любая поверхность, то два закона Декарта сохраняются (но может быть несколько возможных путей).
Обобщение законов Декарта на случай любой сплошной среды.
Случай плана маршрута
Если свет движется в плоскости , мы можем параметризовать его траекторию по абсциссе x (за исключением линии x = constant). Траектория становится функцией y ( x ), а оптический путь записывается О Икс у
L ( В B ) знак равно ∫ В B нет d s знак равно ∫ Икс В Икс B нет ( Икс , у ( Икс ) ) 1 + у ′ ( Икс ) 2 d Икс n \; \ mathrm s = \ int _ ^ > n (x, y (x)) < \ sqrt >> \; \ mathrm x> .
Уравнение Эйлера-Лагранжа, выражающее стационарность траектории для этого интеграла, дает
Мы собираемся решить частный случай, когда n зависит только от x : тогда мы получим ; однако, если обозначить через угол, образованный касательной к кривой с , это условие записывается: нет у ′ 1 + у ′ 2 знак равно против т е >>> = cte> я О Икс
Это своего рода бесконечно малая версия второго закона Декарта, который фактически является локальным переводом принципа Ферма.
Дифференциальное уравнение траектории: . у ′ знак равно k нет 2 - k 2 -k ^ >>>>
Пересечение светового луча в полосе, где показатель преломления обратно пропорционален расстоянию от центра полосы: траектория представляет собой дугу окружности, как показано напротив.
Очевидно, мы обнаруживаем, что при постоянном траектории являются прямыми линиями; но если мы возьмем , кривая просто параметризуется нет нет знак равно ( в Икс ) 1 / α > \ right) ^ >
Например, для (показатель преломления обратно пропорционален абсциссе) получаем α знак равно 1
другими словами, траектории - это круги.
Для (показатель преломления обратно пропорционален квадратному корню из абсциссы) получаем α знак равно 2
< Икс знак равно в 2 k ( 1 - потому что 2 т ) у знак равно в 2 k ( 2 т - грех 2 т ) + б x = (1- \ cos 2t) \\ y = (2t- \ sin 2t) + b \ end >> :
кривая - циклоида . Этот случай исторически интересен: именно этим методом Жан Бернулли доказал, что кривая брахистохрона (минимизирующая время пробега материальной точки) является циклоидой, показав, что проблемы механики и оптики фактически эквивалентны.
Общий случай
Рассмотрим теперь сплошную трехмерную неоднородную среду. Мы показываем, что обобщенные законы Декарта, вытекающие из принципа Ферма, формулируются в следующей форме:
Принцип Ферма
В 1660 г. П. Ферма, сформулировал принцип, который явился обобщенным законом и геометр ической оптики. В простейшей формулировке этот принцип звучит так.

В вакууме скорость света максимальна. В оптической среде с показателем преломления п время прохождения светом того же расстояния увеличивается в п раз. Величина s , равная п po изведению абсолютного показателя преломления n на пройденном расстояние l ( s = nl ), называется оптической длиной пути. Принцип Ферма относится именно к оптической длине пути

Прямолинейность распространения света.
Используя принцип Ферма, можно получить закон прямолинейного распространении света. Свет из одной точки в другую распространяется по крат чайшему расстоянию. В однородной среде кратчайшим оптически и путем является прямая линия.
Однако в неоднородной среде кратчайшим оптическим путем может оказаться некоторая кривая (или ломаная) линия, вдоль которой показатель преломления меньше, чем вдоль геометри ческой прямой. Этим объясняется явление преломления света и ис кривление световых лучей в неоднородной среде — явление ре фракции.
Закон отражения.
Пусть на зеркальную поверхность падает свет из точки А. В точке А' собираются лучи, отраженные от зеркала. Предположим, что свет из точки А в точку А' может распространяться двумя путями — отражаясь от точек О и О'. Время, которое потребуется свету, чтобы пройти из источника А в точку А' через точку О, можно определить из вы ражения
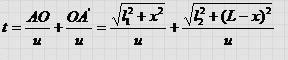
Здесь u — скорость распространения света. Покажем, что время прохождения света по траектории АОА' меньше, чем по любой другой траектории АО'А'.
Продифференцируем выражение и приравняем произ водную нулю в соответствии с принципом Ферма.
Учтем, что sin a = x / AO , sin a ’ = ( L - х) /ОА'. Получим:
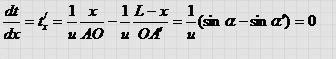
Отсюда получаем sin a = sin a '; а так как оба угла острые, то отсюда следует равенство углов:
Мы получили соотношение, выражающее закон отражения угол отражения a ' равен углу падения a . Из принципа Ферма следует и вторая часть этого закона: отраженный луч лежит в плоскости, проходящей через падающий луч и нормаль сражающей поверхности. Ведь если бы эти лучи лежали в разных плоскостях, то не был бы минимальным путь АОА'.
Закон преломления света
Закон преломления света. Аналогичным образом, используя принцип Ферма, рассмотрим явление, происходящее на границе разд ела двух сред. Пусть в среде I скорость света u 1 , в среде II — u 2 . Для прохождения света из точки А 1 в точку A 2 будет затрачено время
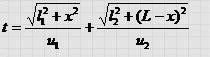
Выберем из всех возможных траекторий распространения света ту, которой соответствует минимальное время распростране ния света. Продифференцировав и положив производную равной пулю, получим:
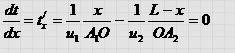
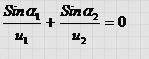
Учитывая, что sin a 1 = x / A 1 O , sin a 2 = ( L - х) /ОА2 получим : Откуда следует :
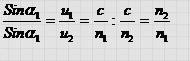
Это и есть закон преломления света. Запишем его в более удобной форме.
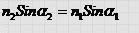
Из построений и принципа Ферма следует также, что преломленный луч лежит в плоскости, проходящей через падающий луч и перпендикуляр к поверхности раздела двух сред.
Рассматривая падение светового пучка на границу раздела двух сред, мы говорили раздельно об отражении и преломлении света. Это было вызвано необходимостью вывода законов отражения и преломления света. Однако практически всегда на границе раздела двух сред световой пучок разделяется на два - отраженный и преломленный.
Читайте также:

