Понятие отношения на множестве кратко
Обновлено: 04.07.2024
Напомним некоторые необходимые в дальнейшем понятия так называемой наивной или интуитивной теории множеств.
Понятие множества
Понятие множества первично, исходно, неопределяемо, т.е. не может быть сведено к другим понятиям. Под множеством понимается совокупность объектов (предметов), которая рассматривается, мыслится как одно целое, как нечто единое. Объекты, составляющие множество, называются его элементами. Множества обозначают заглавными буквами латинского алфавита: , а элементы множеств — малыми латинскими буквами: . Если некоторый объект является элементом множества принадлежит множеству не принадлежит множеству . Символ , обозначается . Символ применяется для обозначения множества всех таких объектов . Если объекты берутся из некоторого множества , обозначается . Например, — множество всех действительных чисел (нетрудно проверить, что это множество есть замкнутый отрезок числовой прямой).
Включение и равенство множеств
Множество . Запись: . Множество собственным подмножеством множества . Обозначение: называется знаком включения .
Множество называется пустым, если оно не содержит ни одного элемента. Существует единственное пустое множество, оно обозначается символом . Значит, для любого множества
Операции над множествами
Разностью множеств , элементами которого являются все те элементы множества
Если дополнением множества
Свойства операций над множествами
Перечислим некоторые наиболее важные свойства операций над множествами и отношения включения множеств:
1) (идемпотентность пересечения);
3) (коммутативность пересечения);
5) (ассоциативность объединения);
6) (ассоциативность пересечения);
7) (дистрибутивность объединения относительно пересечения);
8) (дистрибутивность пересечения относительно объединения);
9) (1-й закон поглощения);
10) (2-й закон поглощения);
11) ;
14) [;
15) ;
16) ;
17) (закон инволюции);
18) ;
19) ;
20) ;
21) ;
22) . Итак, множество
9) Воспользуемся тавтологией из теоремы 3.2, (пункт е): :
11) Воспользуемся тавтологией из теоремы 3.2, (пункт ж): :
20) Воспользуемся тавтологией из теоремы 3.2, (пункт ж):
Проанализируйте приведенную цепочку рассуждений и выявите использованные тавтологии.
Бинарные отношения и функции
Пусть даны два (не обязательно различных) множества Упорядоченной парой , составленной из элементов и , в которой указано, какой элемент является первым, а какой — вторым. Таким образом, упорядоченная пара отлична от упорядоченной пары , если . Упорядоченные пары и называются равными, если и только если и Прямым (или декартовым) произведением двух множеств , таких, что
Бинарным отношением между элементами множеств , таких, что — бинарное отношение и записано , то говорят, что связаны отношением , или в отношении , или для выполняется отношение . Вместо записи используют также запись .
Бинарное отношение функцией, заданной на множестве отображением множества а) для любого , такой, что ;
б) для любых из того, что и , следует, что .
Другими словами, — функция, если для любого , такой, что . Этот единственный элемент называется значением функции для аргумента . Если , то используется запись .
Множество , есть функция (отображение) из или .
Функция называется инъективной (или взаимнооднозначной ), если для любых непременно вытекает равенство аргументов .
Функция называется сюръективной (или отображением найдется хотя бы один .
Функция называется биективной (или биекцией ), если она одновременно инъективна и сюръективна.
Понятие n-арного отношения
Обобщением понятия упорядоченной пары элементов является понятие кортежа (упорядоченного набора) объектов.
Два кортежа и называют равными и пишут , если и только если .
Прямым произведением называется множество
Если , то прямое произведение прямой степенью множества называется любое подмножество прямого произведения .
Другими словами, — функция, если для любых существует единственный элемент , такой, что . Аналогично тому, как это делалось для функции одного аргумента, для функции Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Пусть и – некоторые множества и . Тройка определяет отображение, при котором для . Если множества и совпадают, то отображает множество в себя.
Отношением называется пара , где Так как элементами множества являются упорядоченные пары, то отношение – это множество упорядоченных пар. Поскольку каждая пара связывает два элемента из , то отношение называется Бинарным. Тот факт, что два элемента и из связаны отношением , обозначается или .
Областью определения Бинарного отношения называется множество элементов , для которых существуют такие , что .
Областью значений бинарного отношения называется множество элементов , для которых существуют такие , что .
Для бинарных отношений обычным образом определены теоретико-множественные операции объединения, пересечения, дополнения и т. д. Так, например, Дополнением бинарного отношения между элементами множеств и называется множество .
Обратным Отношением для бинарного отношения называется множество упорядоченных пар , таких, что .
Произведением отношений и называется отношение – совокупность пар , для которых существуют такие элементы , что , а .
Пример 37. Рассмотрим бинарное отношение , где – действительные числа, такие, что . Найти: 1) ; 2) ; 3) ; 4) .
Решение. Очевидно, областью определения и областью значений этого отношения является множество всех действительных чисел.
Обратным отношением к заданному бинарному отношению является отношение , где – действительные числа, такие, что . На рисунках 7 и 8 штриховкой отмечены части плоскости, соответствующие отношениям и соответственно.


Рисунок 7 Рисунок 8
Произведение отношений найдём по определению. Существует такое действительное число , что и , т. е. и , следовательно, или . На рисунке 9 изображена часть плоскости, соответствующая отношению .

Ответ: 1) множество всех действительных чисел; 2) множество всех действительных чисел; 3) совокупность пар , таких, что ; 4) совокупность пар , таких, что .
Отношения классифицируются в зависимости от того, обладают или не обладают они некоторыми свойствами.
Свойства отношений. Пусть , тогда отношение называется:

1) рефлексивным, если – истинно;

2) антирефлексивным, если – ложно;
Наиболее часто используются Бинарные отношения. Рассмотрим прямое произведение множеств A´B

.
Назовем бинарным отношением R из A в B множество пар (a, b), для которых высказывание, связывающее a и b, и определяющее отношение R истинно. В этом случае пишем aRb, (a, b)ÎR или ÎR.
Областью определения бинарного отношения R называется множество

Область значений бинарного отношения R называется множество

.
Очевидно, что DRÍA и GRÍB.
Например, если A - множество жителей Украины, B - множество населенных пунктов Украины, отношение R можно задать высказыванием “быть жителем”, которое определяет пары (a, b)ÎR, aÎA, bÎB такие, что высказывание “ живет в населенном пункте ” является истинным.
Вообще бинарные отношения на множестве X определяют следующим способом:
Определение. Бинарным отношением на множестве X называется всякое подмножество декартова произведения X х X.
Условимся отношения обозначать буквами R, S, Т, Р и др.
Если R - отношения на множестве X, то, согласно определению, R X х X. С другой стороны, если задано некоторое подмножество множества X х X, то оно определяет на множестве X некоторое отношение R.
Отношения задают так же, как соответствия. Отношение можно задать, перечислив пары элементов множества X, находящиеся в этом отношении. Формы представления таких пар могут быть различными - они аналогичны формам задания соответствий. Отличия касаются задания отношений при помощи графа.

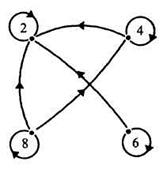
Свойства отношений

Видим, что граф отношения равенства отличается от двух других наличием петель в каждой его вершине. Эти петли - результат того, что отношение равенства отрезков обладает свойством: любой отрезок равен самому себе. Говорят, что отношение равенства обладает свойством рефлексивности или просто, что оно рефлексивно.
Определение. Отношение R на множестве X называется рефлексивным, если о каждом элементе множества X можно сказать, что он находится в отношении R с самим собой.
Используя символы, это отношение можно записать в таком виде:
R рефлексивно на Х xRx для любого х X
Если отношение R рефлексивно на множестве X, то в каждой вершине графа данного отношения имеется петля. Справедливо и обратное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.
Примеры рефлексивных отношений:
- отношение подобия треугольников (каждый треугольник подобен самому себе).
Про отношения перпендикулярности и равенства отрезков говорят, что они обладают свойством симметричности или, просто симметричны.
Определение. Отношение R на множестве X называется симметричным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношении R с элементом х.
Используя символы, это отношение можно записать в таком виде:
R симметрично на X (xRy => yRx)
Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к х. Справедливо и обратное утверждение. Граф, содержащий вместе с каждой стрелкой, идущей от х к у, и стрелку, идущую от у к х, является графом симметричного отношения.
В дополнение к рассмотренным двум примерам симметричных отношений присоединим еще такие:
- отношение параллельности на множестве прямых (если прямая х параллельна прямой у, то и прямая у параллельна прямой х);
- отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).
Определение. Отношение R на множестве X называется антисимметричным, если для различных элементов х и у из множества X выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R с элементом х не находится.
Используя символы, это определение можно записать в таком виде:
антисимметрично на X (xRy и х≠у => )
Граф антисимметричного отношения обладает особенностью: если две вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого соединены только одной стрелкой, есть граф антисимметричного отношения.
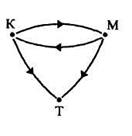
Определение. Отношение R на множестве X называется транзитивным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z.
Используя символы, это определение можно записать в таком виде:
R транзитивно на X (xRy и yRz => xRz)
Граф транзитивного отношения с каждой парой стрелок, идущих от х к у и у к z, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение.
Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны!
Рассмотрим еще одно свойство отношений, которое называют свойством связанности, а отношение, обладающее им, называют связанным.
Определение. Отношение R на множестве X называется связанным, если для любых элементов х и у из множества X выполняется условие: из того, что х и у различны, следует, что либо х находится в отношении R с элементом у, либо элемент у находится в отношении R с элементом х.
Используя символы, это определение можно записать в таком виде:
R связанно на множестве X (х≠у xRy или yRx)
На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.
Существуют отношения, которые свойством связанности не обладают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа хну, что ни число х не является делителем числа у, ни число у не является делителем числа х.
Выделенные свойства позволяют анализировать различные отношения с общих позиций - наличия (или отсутствия) у них тех или иных свойств.
отрезков связанными не являются.
Задача 1. Сформулировать свойства отношения R, заданного при помощи графа (рис. 6).
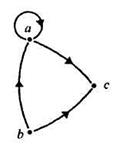
Решение. Отношение R- антисимметрично, так как вершины графа соединяются только одной стрелкой.
Отношение R - транзитивно, так как с парой стрелок, идущих от b к а и от а к с, на графе есть стрелка, идущая от b к с.
Отношение R - связанно, так как любые две вершины соединены стрелкой.
Отношение R свойством рефлексивности не обладает, так как на графе есть вершины, в которых петли нет.
Данное отношение не обладает свойством рефлексивности, потому что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.
Заданное отношение не транзитивно, так как из того, что число х больше числа у на 2, а число у больше числа z на 2, следует, что число х не может быть больше числа z на 2.
Это отношение на множестве натуральных чисел свойством связанности не обладает, так как существуют пары таких чисел х и у, что ни число не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3,5 и 8 и др.
Читайте также:

