Определение производной правила дифференцирования кратко
Обновлено: 05.07.2024
Точки, в которых равенство (5.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка.
Обозначим за Dх разность между двумя значениями аргумента Dх = х2 –х1, а за Df (x) разность между двумя значениями функции Df(x) = f(x2) - f(x1). Тогда, если функция непрерывна, то бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если Dх® 0, то и Df (x) ® 0.
Введем понятие односторонних пределов. Число А называется пределом функции f(x) слева, если х®x0 оставаясь все время меньше х0 (x x0). Запись предела справа
Для непрерывной функции предел слева совпадает с пределом справа и равен значению функции в точке х0
Если хотя бы один из пределов равен бесконечности в точке х = х0 , то говорят, что в этой точке есть вертикальная асимптота. Функция, имеющая на конечном промежутке конечное число разрывов первого рода называется кусочно непрерывной.
Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.
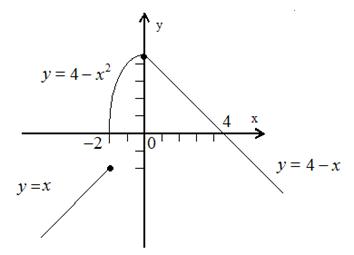
Пример 1. Найти точки разрыва функции.
Решение. На интервалах , и функция непрерывна. Проверке подлежат только точки и .
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.
Вычислим односторонние пределы
Так как односторонние пределы не совпадают, - точка разрыва функции.
- точка непрерывности функции, выполнены все условия непрерывности (рис. 5.1).
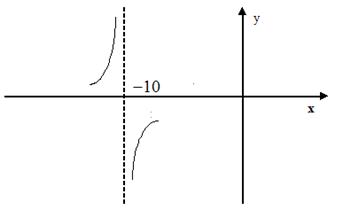
Пример 2. Исследовать поведение функции вблизи точки разрыва. Построить схематический чертеж.
Решение. Область определения функции
Точка разрыва . Найдем односторонние пределы
Знак предела зависит от знаков числителя и знаменателя дроби. В обоих случаях числитель , но знаменатель в пределе слева остается отрицательным, приближаясь к нулю, а в пределе справа, приближаясь к нулю, знаменатель остается положительным. Схематичный чертеж представлен на рис. 5.2.
Пусть задана некоторая функция y = f (x). Выберем в области определения функции два произвольных значения аргумента х их1. Вычислим значения функции f(x) и f(x1). Обозначим за Dх разность между двумя значениями аргумента Dх = х1 – х, (т.е х1 = х +Dх).

Замечание. Dхможет быть как больше нуля, если х1 > х,так именьше нуля, если х1
Уравнение касательной в точке М
В механике производная от пути по времени есть скорость
Производная постояннойС равна нулю
Производная линейной комбинации функцийf1 (x) и f2(x)
где с1 и c2 произвольные постоянные,
равна линейной комбинации производных
Действительно, вычислим приращение функции Dу(x).
Для этого выберем в области определения функции два произвольных значения аргумента х их1. Вычислим соответствующие значения функции у (x1) и у (x) и найдем ее приращение.
Сгруппируем отдельно слагаемые содержащие f1 (x) и f2(x) и вынесем за скобки константы с1 и с2. Выделим приращения функций f1 (x) и f2(x)
Подставим приращение функции Dу(x) (1.5) в формулу (1.1) и учтем правила вычисления пределов:
предел суммы равен сумме пределов,
постоянный множитель можно вынести за знак предела.
Производная произведения функцийу (x) =f(x) g(x) вычисляется по правилу: произведение производной от первой функции на неизменную вторую плюс произведение производной от второй функции на неизменную первую
у (x)’ = (f(x)g(x))¢ = f ¢(x) ּg(x) + f(x) ּg ¢(x). (1.6)
Правило можно обобщить на случай производной произведения n функций
Производная частного двух функцийу (x) = f(x)/g(x) вычисляется по правилу
Глава 1. Определение производной. Правила дифференцирования.
Глава 5. Непрерывность функции. Односторонние пределы.
Функция f(x) называется непрерывнойв точке х0, если она определена в этой точке и некоторой ее окрестности, а также
Точки, в которых равенство (5.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка.
Обозначим за Dх разность между двумя значениями аргумента Dх = х2 –х1, а за Df (x) разность между двумя значениями функции Df(x) = f(x2) - f(x1). Тогда, если функция непрерывна, то бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если Dх® 0, то и Df (x) ® 0.
Введем понятие односторонних пределов. Число А называется пределом функции f(x) слева, если х®x0 оставаясь все время меньше х0 (x x0). Запись предела справа
Для непрерывной функции предел слева совпадает с пределом справа и равен значению функции в точке х0
Если хотя бы один из пределов равен бесконечности в точке х = х0 , то говорят, что в этой точке есть вертикальная асимптота. Функция, имеющая на конечном промежутке конечное число разрывов первого рода называется кусочно непрерывной.
Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.
Пример 1. Найти точки разрыва функции.
Решение. На интервалах , и функция непрерывна. Проверке подлежат только точки и .
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.
Вычислим односторонние пределы
Так как односторонние пределы не совпадают, - точка разрыва функции.
- точка непрерывности функции, выполнены все условия непрерывности (рис. 5.1).

Пример 2. Исследовать поведение функции вблизи точки разрыва. Построить схематический чертеж.
Решение. Область определения функции
Точка разрыва . Найдем односторонние пределы
Знак предела зависит от знаков числителя и знаменателя дроби. В обоих случаях числитель , но знаменатель в пределе слева остается отрицательным, приближаясь к нулю, а в пределе справа, приближаясь к нулю, знаменатель остается положительным. Схематичный чертеж представлен на рис. 5.2.

Пусть задана некоторая функция y = f (x). Выберем в области определения функции два произвольных значения аргумента х их1. Вычислим значения функции f(x) и f(x1). Обозначим за Dх разность между двумя значениями аргумента Dх = х1 – х, (т.е х1 = х +Dх).
Замечание. Dхможет быть как больше нуля, если х1 > х,так именьше нуля, если х1

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная - одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
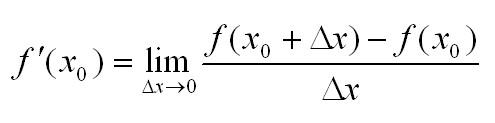
Иначе это можно записать так:
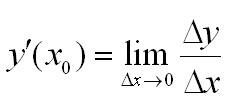
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
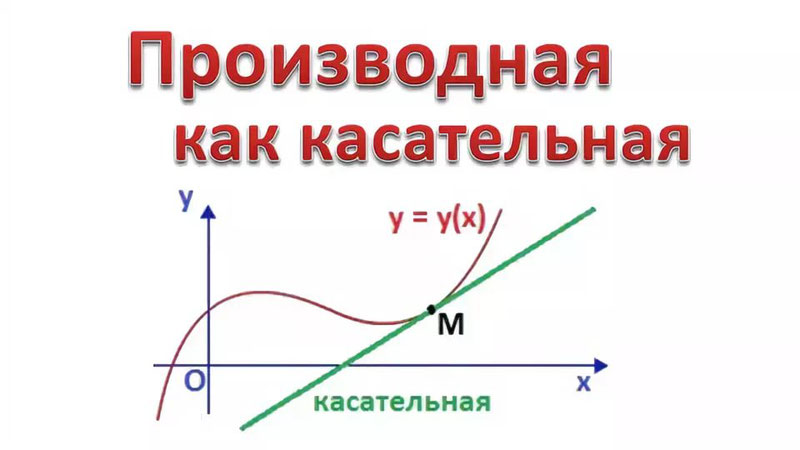
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
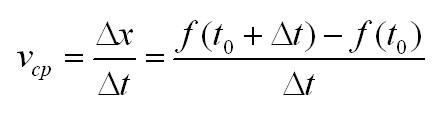
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
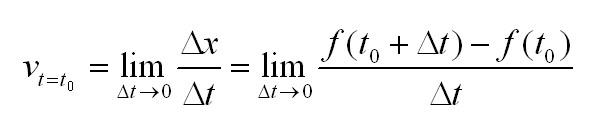
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
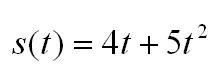
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
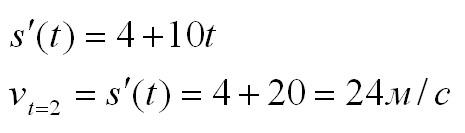
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
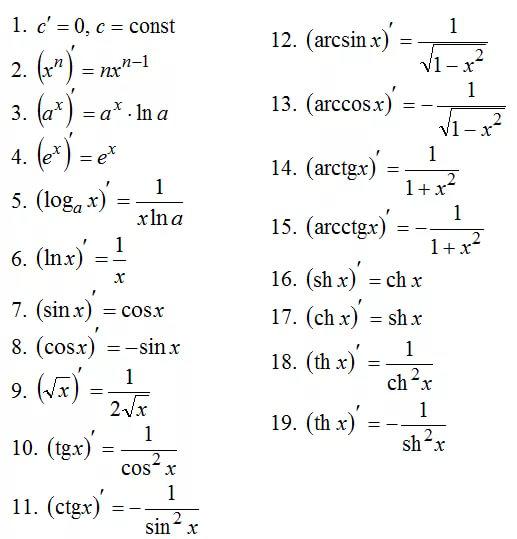
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того - это нужно делать. При решении примеров по математике возьмите за правило - если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
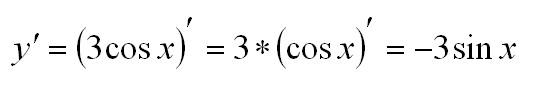
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
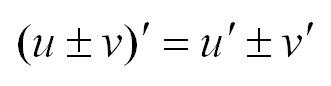
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
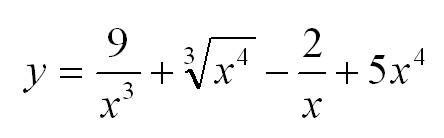
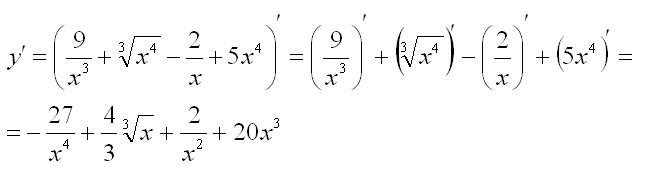
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
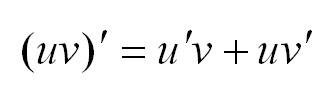
Пример: найти производную функции:
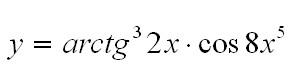
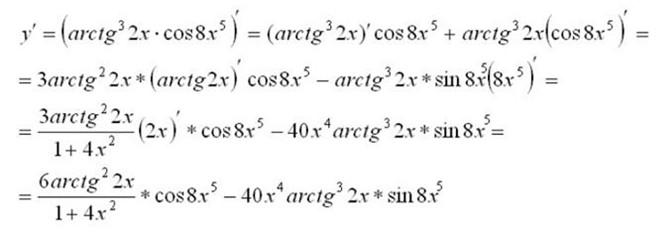
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
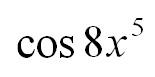
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
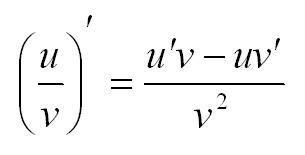
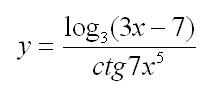
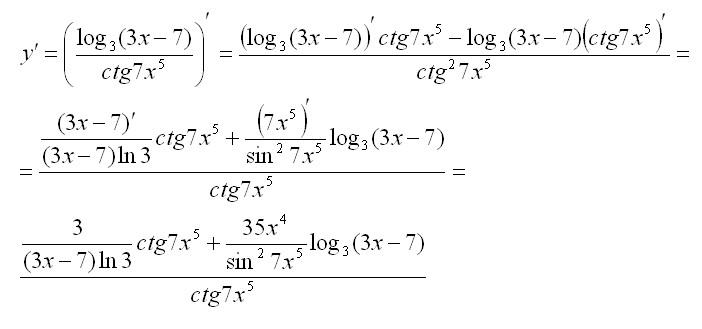
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных.
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции, и, в особенности, бесконечно малые величины. Дело в том, что определение производной базируется на понятии предела, которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций. Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные, в том числе производные сложных функций. Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования, даже не осознавая сущности своих действий.
Понятие возрастания, убывания, максимума, минимума функции
Многие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
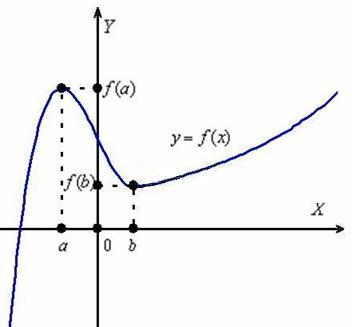
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо. Для простоты полагаем, что функция непрерывна на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает, то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума, то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум, и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции, а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью. И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто, чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Скорость изменения функции
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции, и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание: числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции составляет . То есть, здесь на каждый метр пути приходится в среднем пол метра подъёма.
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым.
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию, которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.
Геометрический смысл производной и дифференциала
Производная функции в точке
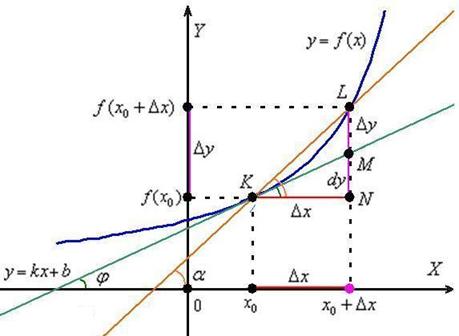
Рассмотрим функцию (синий график), которая определена и непрерывна на некотором интервале, произвольную точку , принадлежащую данному интервалу, и соответствующее значение :
Зададим аргументу функции приращение (красный отрезок) в точке . Обратите внимание, что – это тоже вполне определённая точка нашего интервала (на всякий случай отметил её малиновым цветом). И в этой точке существует своё значение функции .
Приращение аргумента повлекло за собой приращение функции:
(малиновый отрезок)
В данном случае , поскольку в качестве примера выбран промежуток, на котором функция возрастает.
Давайте сразу возьмём на заметку, что нарисовалось в результате проделанных действий. Ну, конечно же, в глаза бросается секущая (коричневая прямая) и прямоугольный треугольник .
Угол наклона секущей к оси я обозначил через и отметил его коричневой дугой в двух местах. Такое внимание к данному углу не случайно – он однозначно определяется приращениями . Рассмотрим прямоугольный треугольник и угол . Согласно школьному определению, тангенс угла равен отношению противолежащего катета к прилежащему катету:
Определение: производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента в этой точке при . Или коротко:
Если данный предел конечен, то функция является дифференцируемой в точке . А то, что в львиной доле случаев предел существует и конечен, скептики убедятся в самом ближайшем будущем.
И, конечно же, не забываем о важнейшей особенности предела, как такового: ПРИНЦИПИАЛЬНЫЙ МОМЕНТ состоит в том, что приращение аргумента стремится к нулю, но нуля не достигает, иными словами, величина бесконечно малА, но не равна нулю!
Геометрический смысл производной
Пожалуйста, возьмите в руки обычную линейку и совместите её ребро с прямой .
Да-да – приложите прямо к экрану монитора, не комплексуйте =) Вместо линейки можно использовать тетрадку, лист бумаги или даже руку.
Теперь, согласно определению производной , медленно двигаем линейку влево к точке , уменьшая тем самым приращение . При этом приращение функции тоже уменьшается: точка будет бесконечно близко приближаться к точке по горизонтали (красному отрезку), и точка – бесконечно близко приближаться к той же точке , но уже по графику функции (синей линии).
В результате секущая стремится занять положение касательной к графику функции в точке . Искомая касательная изображена зелёным цветом.
Таким образом, мы получили строгое определение касательной к графику функции:
Касательная к графику функции в точке – это предельное положение секущей в данной точке.
Вот что матан животворящий делает =)
Развиваем мысль дальше. Вспомним полученную ранее формулу тангенса угла наклона секущей и осуществим в обеих её частях так называемый предельный переход.
В свете рассматриваемых событий (бесконечного уменьшения и нахождения предела ) угол наклона секущей стремится к углу наклона касательной (последний дважды отмечен зелёными дугами). Аналогичное утверждение справедливо и для тангенсов данных углов: . В итоге:
Вывод: производная функции в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке: .
А тангенс угла наклона касательной – это в точности её угловой коэффициент:
В курсе аналитической геометрии выведена формула, по которой можно составить уравнение прямой с угловым коэффициентом:
Учитывая полученное равенство , перепишем уравнение в виде .
Данной формулой мы уже активно пользовались, когда находили уравнение касательной, и сейчас стало ясно, откуда она взялась.
Существование производной в точке и непрерывность функции
По определению: , следовательно, существование производной в точке тесно связано с существованием предела в данной точке.
Я изо всех сил пытался отсрочить этот момент, чтобы не путать посетителей сайта, но рассказать всё равно придётся…. В определении производной ВАЖНЕЙШИМ является тот факт, что приращение аргумента задаётся и в другую сторону. Возьмите карандаш и листок бумаги (не ленимся – так будет в 10 раз понятнее. ). Изобразите координатные оси, примерно такой же график функции и точки .
Таким образом, существование производной в точке геометрически очень удобно ассоциировать с существованием ОБЩЕЙ КАСАТЕЛЬНОЙ в данной точке.
Вывод: из дифференцируемости функции в точке необходимо (обязательно) следует её непрерывность в данной точке.
В заключение параграфа немного об особых случаях.
За более детальной и подробной информацией по сабжу можно обратиться, например, к первому тому Фихтенгольца. НедУрно издание 1962 года, закачивается без проблем.
Раз пошла такая пьянка.
Дифференциал функции в точке и его геометрический смысл
Дифференциалом функции в точке называют главную линейную часть приращения функции (строго говоря, его следовало обозначить или ). На чертеже дифференциал в точке равен длине отрезка .
Давайте снова возьмём в руки линейку и приложим её ребром к монитору на прямую . Двигая линейку влево к точке , уменьшаем приращение . Впрочем, и сам выполню несколько засечек:
По рисунку хорошо видно, что с уменьшением уменьшается и приращение функции (малиновые линии). При этом отрезок занимает всё меньшую и меньшую часть приращения функции , а наш дифференциал – всю бОльшую и бОльшую его часть, именно поэтому его и называют главной частью приращения функции. Настолько главной, что при бесконечно малом дифференциал стремится к полному приращению функции: (соответственно отрезок будет бесконечно малым).
Нетрудно вывести формулу для приближенных вычислений с помощью дифференциала. Рассмотрим прямоугольный треугольник и тангенс угла наклона касательной . Обозначив дифференциал в рассматриваемой точке корректнее через , и учитывая, что , получаем:
Провернём ещё один неожиданный фокус с полученным равенством . Предельно малое значение часто обозначают через , поэтому формула принимает вид . Скинем в знаменатель противоположной части:
Понятие производной функции
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной).
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции, в частности в точках минимума и максимума.
Откуда взялись правила дифференцирования и таблица производных? Невероятно, но все они появились благодаря единственной формуле: . И как это происходит, мы начнём разбирать прямо сейчас.
Действительно, пора переходить к практическим примерам. Ну а это был, пожалуй, первый обстоятельный теоретический материал, который я опубликовал на сайте – вполне можете взять для реферата или курсовика. Только аккуратнее, здесь есть зашифрованное послание для вашего преподавателя =)
Используя определение производной, доказать, что производная константы равна нулю.
Покажем аналитически, что производная функции-константы равна нулю. Рассмотрим произвольное значение , в котором, понятно, . Придадим аргументу приращение: . Функция всё время постоянна, поэтому и приращение функции: . По определению производной в точке:
Найти производную функции по определению.
Рассмотрим произвольное значение , в котором .
Вычислим приращение функции:
По определению производной в точке:
Поскольку в качестве можно взять любое значение , то .
Теперь вам должно быть понятно происхождение и весь неформальный смысл полученного результата.
Используя этот же алгоритм, можно решить задачу в общем виде и доказать, что производная линейной функции равна её угловому коэффициенту:
.
В начале статьи Уравнение прямой на плоскости я проанализировал расположение прямой в зависимости от углового коэффициента. И сейчас получено объяснение данных фактов с точки зрения математического анализа. Действительно, рассмотрим две линейные функции и найдём их производные:
Факт тривиален, но озвучу: касательная к графику линейной функции в каждой точке совпадает с самим графиком данной линейной функции.
Заключительная демонстрационная задача, думаю, развеет все оставшиеся непонятки:
Найти производную функции по определению.
Рассмотрим произвольную точку и соответствующее значение . Зададим приращение и вычислим значение функции в точке :
Найдём приращение функции:
По определению производной в точке:
Поскольку в качестве можно рассмотреть любую точку области определения функции , то проведём замену и получим .
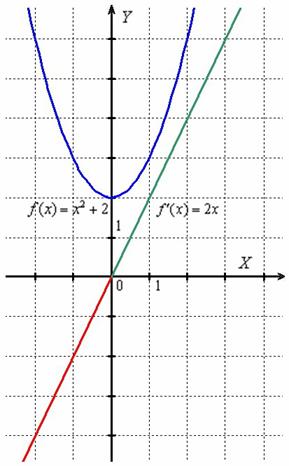
Исходная функция и её производная – это две совершенно разные функции, однако между ними существует чёткая и прозрачная связь:
На интервале производная отрицательна: (красная линия), что говорит об убывании функции на данном интервале. Грубо говоря, ветвь параболы идёт сверху вниз. А на интервале производная положительна: (зелёная линия), значит, функция растёт на этом интервале, и её график идёт снизу вверх.
При производная равна нулю: . Найденное значение показывает, что скорость изменения функции в точке равна нулю (функция не растёт в ней и не убывает). В данном случае здесь минимум функции.
Всё это можно утверждать даже не зная, что такое парабола и как выглядит график функции !
И ещё раз заостряю внимание, что значение производной в точке выражает собой некоторую меру скорости изменения функции в данной точке. Найдём несколько значений производной:
Таким образом, в точке функция убывает, в точке сохраняет скорость постоянной, а в точках – растёт. Причём , поэтому можно сказать (опять даже не зная чертежа!), что в окрестности точки график функции идёт вверх круче, чем вблизи точки .
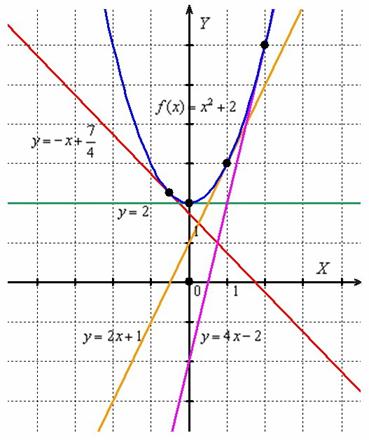
Закрепим геометрический смысл: производная в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке. Не поленюсь, применю формулу четыре раза:
Вот так вот изящно производная характеризует свою функцию.
Наше увлекательное путешествие подошло к концу, и возникает вопрос: в каком направлении двигаться дальше? Это зависит от ваших сегодняшних потребностей:
– Можно потренироваться в нахождении производной по определению. И смех, и грех, но для применения формулы опять же совсем не обязательно понимать, что это производная =)
– Можно отработать и окончательно уяснить геометрический смысл производной на уроке Уравнения касательной и нормали.
– И, наконец, можно перейти в следующий раздел – к статье об экстремумах функции, из-за которой на сайте, собственно, и появилась теория.
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Что такое производная функции
![]()
, то бесконечное количество различных функций усложняют задачу дифференцирования, так как удобно функцию, которую можно представить из различных элементарных функций, дифференцировать основываясь на уже выведенных выражениях для производных этих элементарных функций.
Таблица производных
Таким образом, чтобы работать с производными, необходима таблица производных элементарных функций. Руководствуясь этой таблицей, можно взять производную от какой угодно функции. Но прежде чем работать с таблицей — нужно знать как брать производную функции, есть определенные правила дифференцирования, которые представим в таблице.
Правила дифференцирования
| № правила | Название правила | Правило дифференцирования |
| 1 | Производная постоянной величины | , С-постоянная |
| 2 | Производная суммы | . |
| 3 | Производная произведения постоянной на функцию | , С — постоянная |
| 4 | Производная переменной x | |
| 5 | Производная произведения двух функций | |
| 6 | Производная деления двух функций | |
| 7 | Производная сложной функции |
Таблица производных простых и сложных функций
Теперь таблица производных для элементарных и для сложных функций.
| Номер формулы | Название производной | Основные элементарные функции | Сложные функции |
| 1 | Производная натурального логарифма по x | ||
| 2 | Производная логарифмической функции по основанию a | ||
| 3 | Производная по x в степени n | ||
| 4 | Производная квадратного корня | ||
| 5 | Производная a в степени x | ||
| 6 | Производная e в степени x | ||
| 7 | Производная синуса | ||
| 8 | Производная косинуса | ||
| 9 | Производная тангенса | ||
| 10 | Производная котангенса | ||
| 11 | Производная арксинуса | ||
| 12 | Производная арккосинуса | ||
| 13 | Производная арктангенса | ||
| 14 | Производная арккотангенса |
Примеры нахождения производных
Пример 1
Пользуясь формулами и правилами дифференцирования, найти производную функции: .
![]()
Решение:
Мы использовали правило 2 дифференцирования суммы. Теперь найдем производную каждого слагаемого:
По правилам дифференцирования 3 и 4.
Итак, получим: .
Пример 2
![]()
Решение:
Находим производную, пользуясь правилам дифференцирования 6.
![]()
Ответ:
Пример 3
Найти производную функции
Решение: здесь все просто, мы возьмем производную из таблицы производных.
Ответ:
Пример 4
Найдите производную функции
Решение: Здесь мы уже имеем не простую функцию, а сложную функцию и брать производную мы будем по формуле 8 таблицы производных для сложных функций.
![]()
![]()
Ответ:
Пример 5
![]()
Решение: У нас сложная функция, так как под корнем стоит не просто , а квадратная функция.
![]()
.
Возьмем производную этой функции:
Ответ:
Пример 6
Найдите скорость тела, если траектория его движения задана уравнением м
Решение: скорость тела — это первая производная траектории по времени: . м/с.
Находим скорость тела:
Ответ: 3 м/с.
Итак, таблица производных и правила дифференцирования дают возможность легко брать производные и простых, и сложных функций.
Читайте также:

